Алгоритмы что это такое в информатике
Что такое алгоритм
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В интернете очень часто встречается слово «алгоритм», и для многих оно является загадкой.
Разберемся на понятных и простых примерах с понятием алгоритма (что такое), а также с его видами и применением.
Алгоритм — это.
Алгоритмы окружают нас повсюду. По их принципам существует животный мир, люди, работают компьютеры и механизмы. Некоторые из них очевидны, другие же скрыты от глаз (но это не значит, что их нет).
Алгоритм в информатике — это последовательность действий, которая направлена на достижение окончательного решения проблемы наиболее оптимальными и эффективными способами.
Существует версия, что термин алгоритм произошел от имени древнего ученого Аль-Хорезми, который написал трактат «Книга о сложении и вычитании».
Позднее один из переводчиков на латинский язык неправильно перевел имя ученого и вынес его в название книги — «Алгоритмии о счете индийском». Так этот термин проник в европейские языки и закрепился в них.
Существуют сложные и легкие алгоритмы. Для решения одних не требуется усилий, а для других не хватит и всей мощности компьютеров.
Любые действия, предполагающие определенную последовательность в жизни животных и людей, можно назвать алгоритмом (поиск пищи для животного, поход в магазин за хлебом).
Конечно, животное, ищущее корм, не подозревает, что использует алгоритмы, но действует по определенным правилам (инстинктам), чтобы добыть пропитание:
В информатике и программировании алгоритмы используются для написания программ (что это такое?). Чем качественнее алгоритмы, используемые в программе, тем лучше она работает.
Когда вы начинаете изучать любой язык программирования, то первое, что вам объясняют — это принципы построения алгоритма для будущей программы. Это такие блок-схемы, которые наглядно покажут ход обработки данных и логику вычислений. Без них поначалу будет очень трудно писать программы.
Как все это делается и выглядит на практике отлично показано на приведенном выше видео. Не буду повторяться, а лишь настоятельно посоветую потратить десять минут на его просмотр.
Виды и типы алгоритмов
Линейный алгоритм — это последовательное выполнение инструкций в строгой очередности их расположения (пример, «сделать бутерброд с сыром»).
Ветвления — последовательность действий в соответствии с определенными условиями (если одно условие, то выполняется действие 1, если другой условие, то выполняется действие 2);
Пример: Если идет сильный дождь, тогда возьми зонт, а иначе брать зонт не нужно.
В большинстве случаев слово «иначе» опускается, так как из контекста первой части фразы уже понятна дальнейшая логика.
Пример: Если хотите сообщить что-то важное, позвоните по телефону (в данном случае, очевидно, что если сообщение неважное, то звонить не нужно).
Циклические алгоритмы — это последовательность действий, которую необходимо повторять несколько раз для достижения положительного результата («проверка груш на гнилые и не гнилые»).
Пример: В одном ящике лежат груши, необходимо отобрать гнилые и хорошие. Для этого совершаем следующие действия:
Иногда случаются ситуации, когда цикл начинает бесконечно повторяться. Это называется зацикливанием или бесконечный цикл.
Это происходит в том случае, когда условие не может быть выполнено, тогда цикл замыкается в бесконечное повторение. Стоит отметить, что таких ситуаций следует избегать.
В языках программирования существуют различные виды алгоритмов для решения определенных задач.
К основным видам, которые должен знать каждый начинающий программист, можно отнести те, которые используют методы сортировки и поиска.
Все, что нас окружает построено именно на этих алгоритмах, они считаются простыми для понимания.
Где применяют алгоритмы
В математических науках и информатике это поиск эффективного решения поставленной задачи с использованием инструментов и средств.
Например, даже при решении простой задачки (2 * 6) используются определенные методы и инструменты для получения правильного результата. Самое интересное заключается в том, что ее можно решить несколькими способами: использовав листок и ручку, посчитав на компьютере или выполнив умножение в уме. Наиболее эффективный способ решения этой задачи и будет лучшим алгоритмом в данном случае.
Но такие простые примеры не очень интересны для любителей информатики. Есть гораздо более захватывающие проблемы, волнующие умы многих программистов, и над их решением бьются ученые всего мира.
Задача продавца (коммивояжера)
Существуют более интересные примеры для понимания сложности функционирования алгоритмов. Например, задача коммивояжера.
Дано: одному продавцу необходимо посетить четыре города: например, Москву, Берлин, Лондон, и Сан-Франциско. Продать там товар, а затем вернуться обратно.
Решение задачи выглядит простым. Сначала из Москвы поехать в Берлин, затем посетить Лондон, а потом отправиться в Сан-Франциско и вернуться в Москву.
На самом деле это сложный для компьютера алгоритм. В этих 4-х вариантах скрыто 24 различных комбинаций путешествия для решения задачи. Компьютер высчитывает расстояние от одного города до другого, затем сравнивает варианты и выдает решение.
Но если увеличить количество городов (например, до 100), то компьютер не сможет решить эту задачу, так как вариантов будут миллионы, а на решение понадобится несколько веков.
Но самым интересным является то, что, поняв принцип решения подобной задачи, его можно распространить на все подобные, что расширит знания в области информатики (это что?) и других наук.
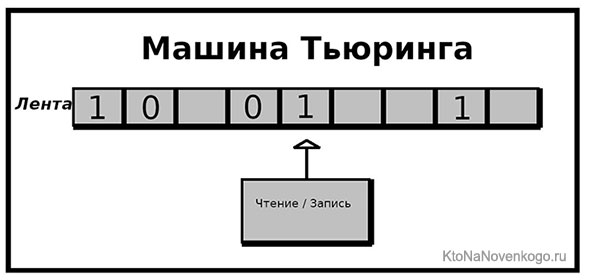
Машина Тьюринга — это основа для понимания алгоритмов
Это абстрактная машина, которую придумал Алан Тьюринг, известный британский ученый. Гениальность этого автомата состоит в следующем. Есть некая лента, состоящая из множества отдельных (бесконечных) ячеек, в которых содержатся данные или биты (0 и 1). Есть считывающее устройство, имеющее доступ к ленте.
В процессе движения устройство снабжено определенными инструкциями, получает доступ к ячейкам, считывает информацию и шагает дальше. Но машина может изменять свои действия, записать другую информацию или передвигаться то в одну, то в другую сторону (на основе стека внутренних инструкций).
В результате исследований таких машин Тьюрингом выдвинута гипотеза о том, что алгоритм при нахождении значений некоторой функции, которая задана в области алфавита, только тогда существует, когда данная функция вычисляется на машине Тьюринга.
Это аксиома, постулат, которые невозможно доказать математическим методом, так как алгоритм — это не точное математическое понятие.
Заключение
Изучение алгоритмов — это важная часть в понимании работы компьютеров. Оно позволяет узнать, как компьютер функционирует, как принимает, обрабатывает данные и выдает необходимый результат.
Понимание принципов работы поможет лучше овладеть компьютерными языками, так как, владея принципами построения и создания эффективных алгоритмов, можно изучить любой язык программирования (как алфавит в иностранных языках).
Изучаете, осваивайте, применяйте алгоритмы. Надеемся, что наша статья помогла вам в этом!
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (7)
Даже не прочитав статью, а прочитав название, сразу ответил правильно на вопрос. Алгоритм — это реально любая последовательность действий, которая позволит достичь цели.
Можно представить даже поход на работу в виде алгоритма. Если вышли вовремя, то идем на трамвай допустим, если опаздываем, то вызываем такси, если погода хорошая, то берем зонтик / не берем и т.д.
Все программирование в принципе построено на алгоритмах.
Чтобы разобраться с алгоритмами в написании программ нужно иметь хорошо развитое логическое мышление, для программиста главное орудие — это не математика, а именно логика.
Проблема ведь и кроется в том, что поменяв местами две инструкции, синтаксис языка программирования не будет нарушен, но будет нарушена логика, и это нарушение компилятор спокойно пропустит. Вот из-за таких логических ошибок и появляются баги в программах.
Я бы не сказал, что бесконечный цикл в программировании нужно избегать, тут всё от задумки программиста зависит. Если мы хотим, чтобы программа начиналась снова и снова, то тут и нужен бесконечный цикл, а выход из него можно предусмотреть с помощью ветвления if и else и оператора break.
Для успешного программирования нужно обладать хорошей логикой, ведь любой алгоритм опирается на логику, а не существует сам по себе.
Я заметил, что многие алгоритмы я не пропускаю через своё сознание, а выполняю их на уровне рефлекса, к примеру, сначала надеваю кофту, а на неё уже куртку, а не наоборот. Все простые алгоритмы именно так и выполняются, без включения осознанности.
Блок-схема — это слишком общий алгоритм, с его помощью можно понять лишь самую общую логику работы программы. Для написания программы этой схемы недостаточно.
Кто же ты такой, алгоритм?
Сегодня довольно легко столкнуться с недобросовестными школьными учебниками, в частности с учебниками по информатике. В главах, посвященных алгоритмам, вы можете найти непосредственно определение алгоритма. Не пояснение, о чем идет речь, не рассказ о предмете, а именно определение. Причем выделенное жирным шрифтом, старательно обведенное в рамку и помеченное какой-нибудь заметной пиктограммой в виде восклицательного знака. Обычно приправлено всё это соусом из кучи обязательных и необязательных свойств, образуя в итоге феерический кавардак. Давайте попытаемся понять, что же такое алгоритм, почему мы не может дать ему конкретного определения и выясним, какие свойства являются обязательными, а какие нет.
Составителей учебников легко понять, ведь на самом деле строгого определения алгоритма не существует, и более того, такого определения быть не может. Но вместо попыток объяснить, что к чему, авторы подсовывают бедным ученикам еще одно задание по зубрежке бесполезных и неправильных терминов. Чтобы не быть голословным, приведу выдержку из одного весьма распространенного учебника:
В университетах дела обстоят получше, однако автору этих строк на курсе по математической логике и теории алгоритмов пришлось столкнуться все с тем же винегретом из определения алгоритма и его свойств. Разберемся, что тут не так.
Бесконечность не предел
Такой же трюк с нумерацией не пройдет для бесконечных непериодических дробей (иррациональных чисел). Допустим такое множество счетное, то есть элементы этого множества можно пронумеровать натуральными числами. Тогда рассмотрим бесконечную десятичную дробь с нулевой целой частью, у которой первая цифра после запятой не равняется цифре на той же позиции у дроби с номером 1, вторая цифра не равняется цифре на второй позиции у дроби с номером 2 и т.д. Тогда полученная дробь будет заведомо отличаться от всех дробей хотя бы одной цифрой. Получается для нее не нашлось номера в нашей бесконечной нумерации! Примененная схема доказательства называется канторовским диагональным методом в честь придумавшего ее математика Георга Кантора.
Про бесконечные дроби
Не стоит делать ошибку, записывая в иррациональные числа все бесконечные дроби. Иррациональными являются только те числа, которые нельзя представить в виде несократимой дроби вида m/n. В десятичной системе счисления дроби 1/3 и 2/7 тоже окажутся бесконечными, однако их «бесконечность« обусловлена выбранной системой счисления. В системе счисления по основанию 21 эти дроби будут иметь конечное представление, а вот, например, дробь 1/2 окажется бесконечной (периодической).
Говорят, что множество бесконечных десятичных дробей имеет мощность континуум, которая обозначается символом ℵ1 (алеф-один). В дальнейшем нам понадобится следующее множество. Рассмотрим некоторый алфавит (конечное множество символов). Теперь представим множество всех конечных цепочек символов алфавита A*. Коль скоро алфавит конечен, и каждая цепочка конечна, то множество таких цепочек счетно (их можно пронумеровать натуральными числами).
На сколько велика бесконечность?
Допустим в наш алфавит вошли все придуманные на земле символы: русский алфавит, японские иероглифы, шумерская клинопись и т.д. Тогда в наше множество войдут все написанные когда-либо книги, все книги, которые будут написаны и все книги, которые никто не стал бы писать (например, хаотичные последовательности символов). Кроме того, представим книгу, толщиной в Солнечную систему и диагональю листа равной диаметру Млечного Пути, набранную 12-м шрифтом. В наше придуманное множество войдут все такие книги, отличающиеся хотя бы одним символов, и не только они, ведь вселенная бесконечна! Кто мешает представить себе книгу, размером в миллиарды световых лет? А все такие книги? Уже на этом этапе воображение может давать сбои, а ведь наше множество всего лишь счетное. Чтобы дополнить множество до континуума, нужно рассмотреть бесконечную книгу, по сравнению с которой, предыдущие книги — детские игрушки. Но и одной бесконечной книги нам не хватит, нужно рассмотреть все бесконечные книги.
Конструктивно оперировать континуальными бесконечностями невозможно. Даже работая со счетными множествами, мы не рассматриваем сами множества, а только говорим, что какой бы не был элемент N, всегда найдется элемент N+1. Если мы ставим себе прикладную задачу, появление в наших рассуждениях континуальной бесконечности должно служить нам «тревожной лампочкой»: осторожно, выход за пределы конструктивного.
Алгоритмы и вычислимость
Компьютер проводит свои вычисления, подчиняясь некоторой программе, которая воплощает собой конструктивную процедуру, или алгоритм. Не сложно догадаться, что алгоритм как раз и есть то правило, по которому вычисляется функция. Можно сказать, функция считается вычислимой, если для нее существует некоторый алгоритм.
Понятия алгоритм и вычислимая функция оказываются настолько заковыристыми, что некоторые составители учебной литературы не утруждают себя попытками разъяснить их суть. Дело в том, что определения алгоритма не существует, и кроме того, существовать не может, иначе пришлось бы выбросить на свалку целый раздел математики — теорию вычислимости. Попробуем разобраться более подробнее.
Частично-рекурсивные функции и тезис Черча
Все началось с того, что математик Давид Гильберт в 1900 году предложил список нерешенных на тот момент математических проблем. Позже выяснилось, что десятая проблема (проблема решения произвольного диофантового уравнения) оказалось неразрешимой, но для доказательства этого факта пришлось составить целую новую математическую теорию. Вопросами того, какие задачи можно конструктивно решить, и что такое конструктивное решение, занялись математики Курт Гедель, Стивен Клини, Алонсо Черч и Алан Тьюринг.
Курт Гедель наиболее известен тем, что сформулировал и доказал 2 теоремы о неполноте. Между прочим, сделал он это в возрасте всего лишь 24 лет.
Как выяснилось выше, континуальные бесконечности не всегда подходят под конструктивные рассуждения, поэтому Гедель и Клини предложили рассматривать только функции натурального аргумента (при необходимости любые функции над счетными множествами можно привести к «натуральным функция» путем замены элементов множеств их номерами). Изучая вычислимость таких функций, Гедель, Клини, Аккерман и другие математики пришли к так называемому классу частично-рекурсивных функций. В качестве определения этого класса рассматривается набор базовых, очень простых функций (константа, увеличение на единицу и проекция, которая сопоставляет функции многих аргументов один из ее аргументов) и операторов, позволяющих из функций строить новые функции (операторы композиции, примитивной рекурсии и минимизации). Слово «частичные» показывает, что эти функции определены лишь на некоторых числах. На остальных они не могут быть вычислены. Попытки расширить класс частично-рекурсивных функций ни к чему не привели, так как введение новых операций приводило к тому, что получалось множество функций, совпадающее с классом частично-рекурсивных. В дальнейшем Алонсо Черч отказался от попыток расширения этого класса, заявив, что, видимо:
Частично-рекурсивные функции соответствуют вычислимым функциям в любом разумном понимании вычислимости.
Это утверждение называют тезисом Черча. Стоит отметить, что тезис Черча не является теоремой или доказанным утверждением. Во-первых, не понятно, что такое «разумное понимание», во-вторых, превратив тезис Черча в доказанный факт, мы лишаем себя перспектив дальнейшего исследования вычислимости и механизмов вычислений. Никто, впрочем, не мешает попробовать определить такой набор операций, который был бы мощнее базиса для частично-рекурсивных функций. Только вот, до сих пор это никому не удавалось сделать.
Ученые долго не могли привести пример частично-рекурсивной функции, не являющейся примитивно-рекурсивной (без оператора минимизации). Наконец это удалось Вильгельму Аккерману. Предложенная функция Аккермана растет так быстро, что количество цифр в десятичной записи числа A(4,4) превосходит количество атомов во Вселенной.
Формальная теория алгоритмов во многом построена аналогично теории вычислимости. Считается, что алгоритм есть некое конструктивное преобразование входного слова (цепочки символов некоторого алфавита) в некоторое выходное слово. Опять же, здесь мы имеем с функциями вида A*->A*. Конечно, предложенное описание не подходит под определение алгоритма, так как неясно, что же такое «конструктивное преобразование». Хоть понятия алгоритма и вычислимой функции близки, не стоит их смешивать. Для одного и того же алгоритма может быть предъявлено сколько угодно его записей на каком-нибудь формальном языке, но соответствующая вычислимая функция всегда одна. Один из основателей формальной теории алгоритмов, Алан Тьюринг, предложил формальную модель автомата, известного как машина Тьюринга. Тезис Тьюринга гласит:
Каково бы не было разумное понимание алгоритма, любой алгоритм, соответствующий такому пониманию, может быть реализован на машине Тьюринга.
Любые попытки построить более мощные автомат заканчивались неудачей: для каждого такого автомата (машина Поста, нормальные алгоритмы Маркова, автоматы с регистрами и несколькими лентами) удавалось построить аналогичную машину Тьюринга. Некоторые ученые объединяют тезис Черча и тезис Тьюринга в тезис Черча-Тьюринга, так как они весьма близки по духу.
С помощью такого незамысловатого автомата можно формализовать любой алгоритм.
Таким образом, определив понятие алгоритма, мы будем вынуждены забыть о тезисе Черча-Тьюринга, и отказаться от целой математической теории, богатой содержанием и подарившую нам множество практических результатов.
Свойства алгоритмов
Мы выяснили, почему у алгоритма не может быть конкретного определения. Однако можно определить свойства, которыми должен обладать каждый алгоритм. К сожалению, в литературе часто смешивают обязательные и необязательный свойств. Разберемся подробнее.
Обязательные свойства
Начнем с обязательных свойств. Алгоритм можно записать в виде конечного текста из символов конечного алфавита. Действительно, бесконечный текст мы не можем записать чисто технически, а раз алгоритмы имеют отношение к конструктивной деятельности, бесконечными они быть не могут. Возможность представить алгоритм в виде конечного текста можно назвать свойством объективности и конечности.
Еще одно достаточно очевидное свойство любого алгоритма — его дискретность. Независимо от исполнителя, исполнение алгоритма представляет собой дискретный процесс, при рассмотрение распадающийся на элементарные действия. Понимать дискретность можно и в том смысле, что любая информация, над которой работает алгоритм может быть представлена в виде текста.
Третье фундаментальное свойство алгоритмов называется детерминированностью. Оно заключается в том, что следовать предписанной процедуре можно только одним способом. Единственное, что может повлиять на ход выполнения — это исходные данные, однако при одних и тех же исходных данных, алгоритм всегда выдает один и тот же результат.
Эти три свойства присущи всем алгоритмам. Если нарушено хотя бы одно из них, перед нами уже не алгоритм. С натяжкой к обязательным свойствам можно добавить понятность для исполнителя, хотя это уже на грани фола. По большей части. это относится не к самому алгоритму, а к его записи.
«Винегрет» из свойств из того же учебника по информатике.
Необязательные свойства
Наряду с обязательными свойствами, алгоритм может обладать некоторыми частными свойствами, которые вовсе не обязательны. Начнем с массовости. Конечно, хочется, чтобы алгоритмы решали классы задач в зависимости от входных данных. Однако существуют алгоритмы, которые вообще не зависят от входных данных, например всем известный вывод на экран «Hello world». Как среди вычислимых функций существуют константные, так и среди алгоритмов существуют генераторы единственного результата.
Теперь рассмотрим широко распространенное убеждение, что алгоритмы должны обладать свойством правильности и завершаемости. Начнем с правильности. Такое свойство попросту невозможно формализовать, так как отсутствуют критерии этой правильности. Наверняка, многие из вас сталкивались с ситуацией, когда программист считает программу правильной, а заказчик нет. С завершаемостью дела обстоят интереснее. Рассмотрим термин «применимость« — алгоритм называется применимым к слову, если, получив на вход это слово, он завершается за конечное число шагов. Самое интересное то, что проблема применимости является алгоритмически неразрешимой, то есть невозможно составить алгоритм, которые определял бы по записи алгоритма и входному слову, завершится ли он за конечное число шагов. Никто не мешает вам составить программу, состоящую только из одного бесконечного цикла. И эта программа все еще будет алгоритмом.
Про зависающие программы
Программы, которые не могут зациклиться, на самом деле входят в класс примитивно-рекурсивных — подмножество частично-рекурсивного класса. Отличает их отсутствия оператора минимизации. Он то и вносит пикантности. Если вы используете «неарифметический цикл» while или рекурсию, для которых нельзя заранее определить, сколько раз они выполняться, то ваша программа сразу переходит из класса примитивно-рекурсивных в класс частично-рекурсивных.
Теперь перейдем к пресловутой последовательности шагов. Дело в том, что алгоритм может быть представлен в любой из имеющихся формальных систем (частично-рекурсивные функции, машина Тьюринга, лямбда-исчисление и т.д.). Воплощение алгоритма в виде компьютерной программы далеко не всегда будет описанием последовательности шагов. Здесь все зависит от парадигмы программирования. В императивной парадигме программисты действительно оперируют последовательностью действий. Однако существуют и другие парадигмы, такие как функциональная (привет Haskell программистам), где нету никаких действий, а лишь функции в сугубо математическом смысле, или чистая объектно-ориентированная, которая основана не на «последовательности действий», а на обмене сообщениями между абстрактными объектами.
Заключение
Иногда мир устроен несколько сложнее, чем хотелось бы. Существующие формализмы в теории алгоритмов не более чем абстрактные математические системы, наподобие геометрии Евклида или теории вероятности, тогда как понятие вычислимости, возможно, находится вне математики и является свойством нашей Вселенной наряду со скоростью света и законом всемирного тяготения. И хотя, скорее всего, нам так и не удастся ответить на вопрос, что такое алгоритмы и вычислимость, попытки найти ответ на этот вопрос оказались более ценными, чем возможный однозначный ответ.
Материал данной статьи во многом опирается на 1-ый том «Программирование: введение в профессию» А. В. Столярова. Тем, кто хочет подробнее изучить вопросы, связанные с алгоритмами и теорией вычислимости, кроме этой книги, советую Босс В «От Диофанта до Тьюринга» и трехтомник А. Шеня по математической логике и теории алгоритмов.
Дата-центр ITSOFT — размещение и аренда серверов и стоек в двух дата-центрах в Москве. За последние годы UPTIME 100%. Размещение GPU-ферм и ASIC-майнеров, аренда GPU-серверов, лицензии связи, SSL-сертификаты, администрирование серверов и поддержка сайтов.