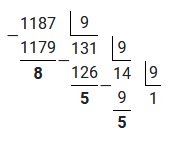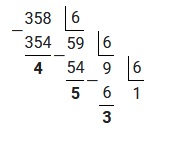число 7 в десятичной системе счисления при переводе его в циклический код имеет вид
Перевод чисел из одной системы счисления в другую
Данный конвертер переводит числа между наиболее популярными системами счисления: десятичной, двоичной, восьмеричной, шестнадцатеричной.
Существуют и другие системы счисления, но мы не стали включать их в конвертер из-за низкой популярности.
Для указания системы счисления при записи числа используется нижний индекс, который ставится после числа:
20010 = 110010002 = 3108 = C816
Кратко об основных системах счисления
Десятичная система счисления. Используется в повседневной жизни и является самой распространенной. Все числа, которые нас окружают представлены в этой системе. В каждом разряде такого числа может использоваться только одна цифра от 0 до 9.
Двоичная система счисления. Используется в вычислительной технике. Для записи числа используются цифры 0 и 1.
Восьмеричная система счисления. Также иногда применяется в цифровой технике. Для записи числа используются цифры от 0 до 7.
Перевод в десятичную систему счисления
Перевод из десятичной системы счисления в другие
Делим десятичное число на основание системы, в которую хотим перевести и записываем остатки от деления. Запишем полученные остатки в обратном порядке и получим искомое число.
Переведем число 37510 в восьмеричную систему:
Перевод из двоичной системы в восьмеричную
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
Перевод из двоичной системы в шестнадцатеричную
Также как и в первом способе разбиваем число на группы по 4 цифры. Заменим полученные группы (тетрады) на соответствующие цифры шестнадцатеричной системы, используя таблицу тетрад:
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Перевод из восьмеричной системы в двоичную
Каждый разряд восьмеричного числа будем делить на 2 и записывать остатки в обратном порядке, формируя группы по 3 разряда двоичного числа. Если в группе получилось меньше 3 разрядов, тогда дополняем нулями. Записываем все группы по порядку, отбрасываем ведущие нули, если имеются, и получаем двоичное число.
Используем таблицу триад:
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады. Ведущие нули самой первой триады отбрасываются.
Перевод из шестнадцатеричной системы в двоичную
Аналогично переводу из восьмеричной в двоичную, только группы по 4 разряда.
Используем таблицу тетрад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Тетрада | 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
Каждую цифру исходного числа заменяется на соответствующие тетрады. Ведущие нули самой первой тетрады отбрасываются.
Перевод из восьмеричной системы в шестнадцатеричную и наоборот
Такую конвертацию можно осуществить через промежуточное десятичное или двоичное число. То есть исходное число сначала перевести в десятичное (или двоичное), и затем полученный результат перевести в конечную систему счисления.
Перевод чисел в различные системы счисления с решением
Исходное число записано в -ой системе счисления.
Хочу получить запись числа в -ой системе счисления.
Системы счисления
Системы счисления делятся на два типа: позиционные и не позиционные. Мы пользуемся арабской системой, она является позиционной, а есть ещё римская − она как раз не позиционная. В позиционных системах положение цифры в числе однозначно определяет значение этого числа. Это легко понять, рассмотрев на примере какого-нибудь числа.
Пример 1. Возьмём число 5921 в десятичной системе счисления. Пронумеруем число справа налево начиная с нуля:
| Число: | 5 | 9 | 2 | 1 |
| Позиция: | 3 | 2 | 1 | 0 |
Пример 2. Рассмотрим вещественное десятичное число 1234.567. Пронумеруем его начиная с нулевой позиции числа от десятичной точки влево и вправо:
| Число: | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Позиция: | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Перевод чисел из одной системы счисления в другую
Наиболее простым способом перевода числа с одной системы счисления в другую, является перевод числа сначала в десятичную систему счисления, а затем, полученного результата в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
Для перевода числа из любой системы счисления в десятичную достаточно пронумеровать его разряды, начиная с нулевого (разряд слева от десятичной точки) аналогично примерам 1 или 2. Найдём сумму произведений цифр числа на основание системы счисления в степени позиции этой цифры:
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления целую и дробную части числа нужно переводить отдельно.
Перевод целой части числа из десятичной системы счисления в другую систему счисления
Целая часть переводится из десятичной системы счисления в другую систему счисления с помощью последовательного деления целой части числа на основание системы счисления до получения целого остатка, меньшего основания системы счисления. Результатом перевода будет являться запись из остатков, начиная с последнего.
Рассмотрим перевод правильных десятичных дробей в различные системы счисления.
Перевод дробной части числа из десятичной системы счисления в другую систему счисления
Напомним, правильной десятичной дробью называется вещественное число с нулевой целой частью. Чтобы перевести такое число в систему счисления с основанием N нужно последовательно умножать число на N до тех пор, пока дробная часть не обнулится или же не будет получено требуемое количество разрядов. Если при умножении получается число с целой частью, отличное от нуля, то целая часть дальше не учитывается, так как последовательно заносится в результат.
Programforyou — это сообщество, в котором Вы можете подтянуть свои знания по программированию, узнать, как эффективно решать те или иные задачи, а также воспользоваться нашими онлайн сервисами.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Системы счисления
Система счисления — это совокупность правил записи чисел посредством конечного набора символов (цифр).
Системы счисления бывают:
Непозиционные системы счисления
Примеры: унарная, римская, древнерусская и др.
Позиционные системы счисления
Основание системы счисления —
количество различных цифр, используемых в этой системе.
отношение количественного эквивалента цифры в этом разряде к количественному эквиваленту той же цифры в нулевом разряде
где i — номер разряда, а s — основание системы счисления.
Разряды числа нумеруются справа налево, причем младший разряд целой части (стоящий перед разделителем — запятой или точкой) имеет номер ноль. Разряды дробной части имеют отрицательные номера:
По определению веса разряда
где i — номер разряда, а s — основание системы счисления.
Тогда, обозначив цифры числа как ai, любое число, записанное в позиционной системе счисления, можем представить в виде:
Например, для системы счисления с основанием 4:
Выполнив вычисления, мы получим значение исходного числа, записанное в десятичной системе счисления (точнее, в той, в которой производим вычисления). В данном случае:
= 1⋅64 + 3⋅16 + 0⋅4 + 2⋅1 + 2⋅0,25 =
= 64 + 48 + 2 + 0,5 = 114,5
Таким образом, для перевода числа из любой системы счисления в десятичную следует:
Вспомним пример перевода из системы счисления с основанием 4 в десятичную:
13024 = 1⋅4 3 + 3⋅4 2 + 0⋅4 1 + 2⋅4 0 = 114
Иначе это можно записать так:
114 = ((1 ⋅ 4 + 3) ⋅ 4 + 0) ⋅ 4 + 2 = 13024
Отсюда видно, что при делении 114 на 4 нацело в остатке должно остаться 2 — это младшая цифра при записи в четверичной системе. Частное же будет равно
Деление его на 4 даст остаток — следующую цифру (0) и частное 1 ⋅ 4 + 3. Продолжая действия, получим аналогичным образом и оставшиеся цифры.
В общем случае для перевода целой части числа из десятичной системы счисления в систему с каким-либо другим основанием необходимо:
Перевод из десятичной системы в любую другую
Перед тем как перейти к алгоритму перевода, вспомним алфавит популярных систем счисления:
| Основание | Название | Алфавит |
|---|---|---|
| 2 | Двоичная | 0, 1 |
| 8 | Восьмеричная | 0, 1, 2, 3, 4, 5, 6, 7 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Для перевода чисел из десятичной системы в любую другую, воспользуемся соответствующим алгоритмом. Важно заметить, что алгоритм перевода целых и дробных чисел будет отличаться.
Алгоритм перевода целых десятичных чисел в систему счисления с основанием q
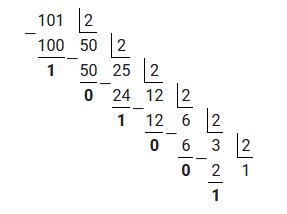
Пример 1 : перевести десятичное число 101 в двоичную систему счисления
Для наглядности произведем деление «столбиком». Решение будет выглядеть следующим образом:
Исходя из вышеприведенного алгоритма, полученные остатки необходимо записать в обратном порядке.
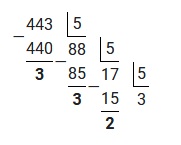
Пример 2 : перевести десятичное число 443 в пятеричную систему счисления
Аналогично предыдущему примеру, произведем деление «столбиком». Решение будет выглядеть следующим образом:
Полученные остатки необходимо записать в обратном порядке.
Пример 3 : перевести десятичное число 1187 в девятеричную систему счисления
Решение будет выглядеть следующим образом:
Алгоритм перевода десятичной дроби в q-ичную систему
Пример 4: перевести число 0,15 в троичную систему.
Решение будет выглядеть следующим образом:
0.15 ∙ 3 = 0.45 (0)
0.45 ∙ 3 = 1.35 (1)
0.35 ∙ 3 = 1.05 (1)
0.05 ∙ 3 = 0.15 (0)
0.15 ∙ 3 = 0.45 (0)
0.45 ∙ 3 = 1.35 (1)
0.35 ∙ 3 = 1.05 (1)
0.05 ∙ 3 = 0.15 (0)
0.15 ∙ 3 = 0.45 (0)
0.45 ∙ 3 = 1.35 (1)
0.35 ∙ 3 = 1.05 (1)
В данном примере можно продолжить вычисления, но зачастую, такой точности будет достаточно.
Перевод дробного десятичного числа в q-ичную систему
Для того чтобы перевести десятичное число, содержащее дробную часть, необходимо отдельно перевести целую часть и отдельно дробную.
Пример 5: перевести число 358,201 из десятичной системы в шестиричную
Для решения примера потребуется отдельно перевести 358 и отдельно 0,201 из десятичной системы в шестиричную, используя вышеизложенные алгоритмы. Таким образом переведя 358, получим:
Перевод десятичной дроби 0,201 выглядит так:
0.201 ∙ 6 = 1.206 (1)
0.206 ∙ 6 = 1.236 (1)
0.236 ∙ 6 = 1.416 (1)
0.416 ∙ 6 = 2.496 (2)
0.496 ∙ 6 = 2.976 (2)
0.976 ∙ 6 = 5.856 (5)
0.856 ∙ 6 = 5.136 (5)
0.136 ∙ 6 = 0.816 (0)
0.816 ∙ 6 = 4.896 (4)
0.896 ∙ 6 = 5.376 (5)
0.376 ∙ 6 = 2.256 (2)
Теперь осталось соединить результаты перевода. Таким образом: 358.20110=1354.111225504526