Что показывает диаграмма дерева узлов
1.2.5. Диаграммы дерева узлов и FEO
1.2.5. Диаграммы дерева узлов и FEO
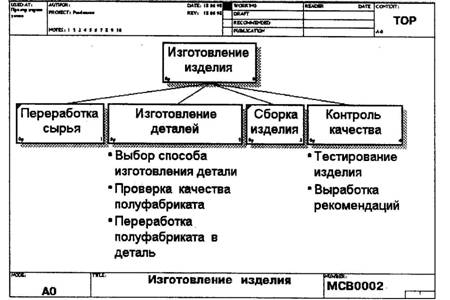
Рис. 1.25. Диаграмма дерева узлов
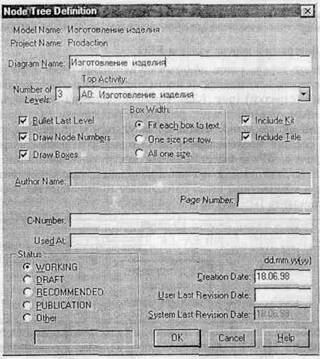
Для создания диаграммы дерева узлов следует выбрать в меню пункт Insert/Node Tree. Возникает диалог формирования диаграммы дерева узлов Node Tree Definition (рис. 1.26).
Рис. 1.26. Диалог настройки диаграммы дерева узлов
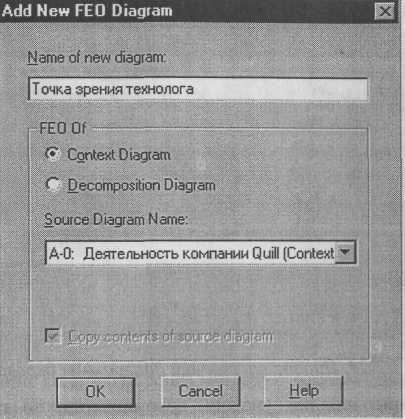
Рис. 1.27. Диалог создания FEO-диаграммы
Новая диаграмма получает номер, который генерируется автоматически (номер родительской диаграммы по узлу + постфикс F, например A1F).
Читайте также
14.4.5. Обход дерева: twalk()
14.4.5. Обход дерева: twalk() Функция twalk() объявлена в следующим образом:typedef enum < preorder, postorder, endorder, leaf >VISIT;void twalk(const void *root, void (*action)(const void *nodep, const VISIT which,const int depth));Первый параметр является корнем дерева (не указателем на корень). Второй является указателем на функцию
14.4.6. Удаление вершины дерева и удаление дерева: tdelete() и tdestroy()
14.4.6. Удаление вершины дерева и удаление дерева: tdelete() и tdestroy() Наконец, вы можете удалить элементы из дерева и, на системах GLIBC, удалить само дерево целиком:void *tdelete(const void *key, void **rootp,int (*compare)(const void*, const void*));/* Расширение GLIBC, в POSIX нет: */void tdestroy(void *root, void (*free_node)(void *nodep));Аргументы
6.3. Влияние семантики и DOM-дерева
6.3. Влияние семантики и DOM-дерева Давайте рассмотрим сейчас другой вопрос, а именно: как быстро браузер создает DOM-дерево в зависимости от наличия в нем элементов с id или class?Для этого мы подготовим 3 набора HTML-файлов. Первый будет содержать 10000 элементов, у которых только
Графики влияния DOM-дерева
Графики влияния DOM-дерева Ниже приведены разделенные графики по средневзвешенному (естественно, основную роль играет Internet Explorer, ибо сейчас им пользуются от 50% до 70% посетителей наших сайтов) времени создания документа (рис. 6.1) Рис. 6.1. Скорость создания документа,
9.3.1. Реализация двоичного дерева
9.3.1. Реализация двоичного дерева Ruby позволяет реализовать двоичное дерево разными способами. Например, хранить значения узлов можно в массиве. Но мы применим более традиционный подход, характерный для кодирования на С, только указатели заменим ссылками на объекты.Что
Создание бинарного дерева
Создание бинарного дерева Само по себе создание бинарного дерева тривиально. В простейшем случае корневой узел бинарного дерева определяет все бинарное дерево.varMyBinaryTree : PtBinTreeNode;Если MyBinaryTree равен nil, никакого бинарного дерева не существует, поэтому это значение служит
Удаление из сортирующего дерева
1.2.5. Диаграммы дерева узлов и FEO
1.2.5. Диаграммы дерева узлов и FEO Диаграмма дерева узлов показывает иерархию работ в модели и позволяет рассмотреть всю модель целиком, но не показывает взаимосвязи между работами (стрелки) (рис. 1.2.23). Процесс создания модели работ является итерационным, следовательно,
1.4.3. Организационные диаграммы и диаграммы Swim Lane
4.4. Упражнение 4. Создание диаграммы узлов
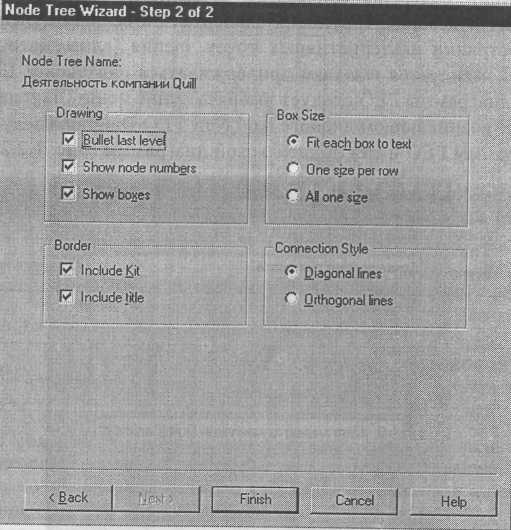
4.4. Упражнение 4. Создание диаграммы узлов Перед выполнением упражнения 4 внимательно прочитайте подраздел 1.2.5.Выберите меню Diagram/Add Node Tree. В первом диалоге гида Node Tree Wizard внесите имя диаграммы, укажите диаграмму корня дерева и количество уровней (рис. 4.4.1). Рис. 4.4.1.
Узлы дерева XML-документа
Узлы дерева XML-документа Корневой узел Корневой узел XML-документа — это узел, который является корнем дерева документа. Не следует путать его с корневым элементом документа, поскольку помимо корневого элемента дочерними узлами корня также являются инструкции по
Копирование узлов
Копирование узлов Преобразование может включать в себя не только создание новых, но и копирование существующих узлов. Для этого можно использовать элементы xsl:copy и xsl:copy-of, использование которых будет подробно разобрано
Диаграмма дерева узлов Node Tree Diagram
ДЕРЕВО УЗЛОВ — представление отношений между родительскими и дочерними узлами модели IDEF0 в форме древовидного графа.
ДИАГРАММЫ ДЕРЕВА УЗЛОВ – это диаграммы, по-казывающие не взаимосвязи между функциями (стрелки), а иерархическую зависимость функций. Диаграмма узлов использует традиционное дерево иерархий, в котором верхний узел (блок) соответствует контекстной диаграмме, а нижний уровень – декомпозицию потомков.
Диаграмму узлов дерева добавляется в модель для демонстрации взаимосвязи всех родительских диаграмм и диаграмм-потомков в виде иерархии блоков в модели, что позволяет рассмотреть всю модель целиком.
Диаграмм деревьев узлов может быть в модели сколь угодно много, поскольку дерево может быть построено на произвольную глубину и не обязательно с корня. Имя дерева узлов по умолчанию совпадает с именем блока верхнего уровня, а номер диаграммы автоматически генерируется как номер узла верхнего уровня плюс буква «N», например A0N.
Если в модели создается два дерева узлов, имеющие в качестве верхнего уровня одну и ту же функцию, то по умолчанию диаграммы получат идентичные номер и имя. Поэтому рекомендуется при создании диаграммы дерева узлов задавать имя диаграммы, отличное от значения по умолчанию.
Процесс создания модели функций является итерационным, следовательно, функции могут менять свое расположение в дереве узлов многократно. Чтобы не запутаться и проверить позиции, следует после каждого изменения создавать диаграмму дерева узлов.
При создании дерева узлов обязательно указывается имя диаграммы, т.к. если в нескольких диаграммах в качестве корня на дереве узлов использовать одну и ту же функцию, то все эти диаграммы будут иметь одинаковый номер (номер узла + постфикс N, например AON). В этом случае их можно будет различить по имени.
1.2.5. Диаграммы дерева узлов и FEO
1.2.5. Диаграммы дерева узлов и FEO
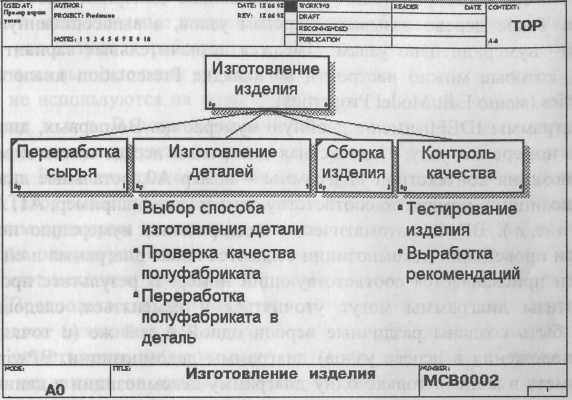
Рис. 1.2.23. Диаграмма дерева узлов
Рис. 1.2.24. Диалог настройки диаграммы дерева узлов
Рис. 1.2.25. Диалог создания FEO-диаграммы
Новая диаграмма получает номер, который генерируется автоматически (номер родительской диаграммы по узлу + постфикс F, например A1F).
Читайте также
14.4.5. Обход дерева: twalk()
14.4.5. Обход дерева: twalk() Функция twalk() объявлена в следующим образом:typedef enum < preorder, postorder, endorder, leaf >VISIT;void twalk(const void *root, void (*action)(const void *nodep, const VISIT which,const int depth));Первый параметр является корнем дерева (не указателем на корень). Второй является указателем на функцию
14.4.6. Удаление вершины дерева и удаление дерева: tdelete() и tdestroy()
14.4.6. Удаление вершины дерева и удаление дерева: tdelete() и tdestroy() Наконец, вы можете удалить элементы из дерева и, на системах GLIBC, удалить само дерево целиком:void *tdelete(const void *key, void **rootp,int (*compare)(const void*, const void*));/* Расширение GLIBC, в POSIX нет: */void tdestroy(void *root, void (*free_node)(void *nodep));Аргументы
6.3. Влияние семантики и DOM-дерева
6.3. Влияние семантики и DOM-дерева Давайте рассмотрим сейчас другой вопрос, а именно: как быстро браузер создает DOM-дерево в зависимости от наличия в нем элементов с id или class?Для этого мы подготовим 3 набора HTML-файлов. Первый будет содержать 10000 элементов, у которых только
Графики влияния DOM-дерева
Графики влияния DOM-дерева Ниже приведены разделенные графики по средневзвешенному (естественно, основную роль играет Internet Explorer, ибо сейчас им пользуются от 50% до 70% посетителей наших сайтов) времени создания документа (рис. 6.1) Рис. 6.1. Скорость создания документа,
9.3.1. Реализация двоичного дерева
9.3.1. Реализация двоичного дерева Ruby позволяет реализовать двоичное дерево разными способами. Например, хранить значения узлов можно в массиве. Но мы применим более традиционный подход, характерный для кодирования на С, только указатели заменим ссылками на объекты.Что
Создание бинарного дерева
Создание бинарного дерева Само по себе создание бинарного дерева тривиально. В простейшем случае корневой узел бинарного дерева определяет все бинарное дерево.varMyBinaryTree : PtBinTreeNode;Если MyBinaryTree равен nil, никакого бинарного дерева не существует, поэтому это значение служит
Удаление из сортирующего дерева
1.2.5. Диаграммы дерева узлов и FEO
1.2.5. Диаграммы дерева узлов и FEO Диаграмма дерева узлов показывает иерархию работ в модели и позволяет рассмотреть всю модель целиком, но не показывает взаимосвязи между работами (стрелки) (рис. 1.2.23). Процесс создания модели работ является итерационным, следовательно,
1.4.3. Организационные диаграммы и диаграммы Swim Lane
4.4. Упражнение 4. Создание диаграммы узлов
4.4. Упражнение 4. Создание диаграммы узлов Перед выполнением упражнения 4 внимательно прочитайте подраздел 1.2.5.Выберите меню Diagram/Add Node Tree. В первом диалоге гида Node Tree Wizard внесите имя диаграммы, укажите диаграмму корня дерева и количество уровней (рис. 4.4.1). Рис. 4.4.1.
Узлы дерева XML-документа
Узлы дерева XML-документа Корневой узел Корневой узел XML-документа — это узел, который является корнем дерева документа. Не следует путать его с корневым элементом документа, поскольку помимо корневого элемента дочерними узлами корня также являются инструкции по
Копирование узлов
Копирование узлов Преобразование может включать в себя не только создание новых, но и копирование существующих узлов. Для этого можно использовать элементы xsl:copy и xsl:copy-of, использование которых будет подробно разобрано