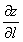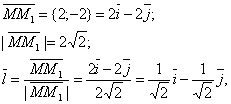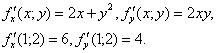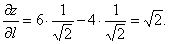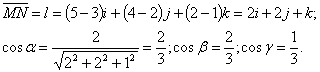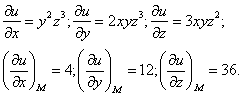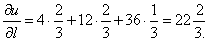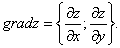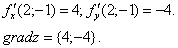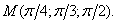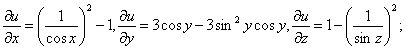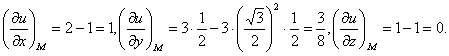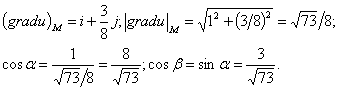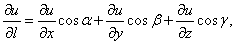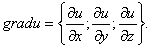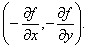Что показывает градиент функции
Нахождение градиента вектор-функции
Дата публикации Oct 20, 2018
ВЧасть 1Нам поставили задачу: вычислить градиент этой функции потерь:
Градиент скалярной функции
Скажи, что у нас есть функция,f (x, y) = 3x²y, Наши частные производные:
Если мы организуем эти части в горизонтальный вектор, мы получимградиентизР (х, у), или∇ f (x, y):
6yxэто изменение вР (х, у)в отношении изменения вИкс, в то время как3x²это изменение вР (х, у)в отношении изменения вY,
Что происходит, когда у нас есть две функции? Давайте добавим еще одну функцию,g (x, y) = 2x + y⁸, Частные производные:
Таким образом, градиент g (x, y):
Представляющие функции
Когда у нас есть несколько функций с несколькими параметрами, часто полезно представлять их более простым способом. Мы можем объединить несколько параметров функций в один векторный аргумент,Иксэто выглядит следующим образом:
Следовательно,Р (х, у, г)станетF (x₁, x₂, x₃)который становитсяе (Икс).
Мы также можем объединить несколько функций в вектор, например так:
Для нашего предыдущего примера с двумя функциями,f (x, y) ⇒ f (Икс)а такжеg (x, y) ⇒ g (Икс).Здесь векторИкс= [x₁, x₂], гдеx₁ = х, а такжеx₂ = у, Чтобы упростить его еще больше, мы можем объединить наши функции: [f (Икс),г(Икс)] = [f₁ (Икс), f₂ (Иксзнак равноf (x) = y.
Зачастую количество функций и количество переменных будет одинаковым, поэтому для каждой переменной существует решение.
Градиент вектор-функции
Теперь, когда у нас есть две функции, как мы можем найти градиент обеих функций? Если мы организуем оба их градиента в одну матрицу, мы переместимся из векторного исчисления в матричное исчисление. Эта матрица и организация градиентов нескольких функций с несколькими переменными, известна какМатрица Якобиана,
Есть несколько способов представления якобиана. Этот макет, где мы укладываем градиенты по вертикали, известен какмакет числителя, но другие документы будут использоватьрасположение знаменателя, который просто переворачивает его по диагонали:
Градиент функции идентичности
Давайте возьмем функцию идентичности,у = ф (х) = х, гдеFi (Икс) = xiи найдите его градиент:
Так же, как мы создали наш предыдущий якобиан, мы можем найти градиенты каждой скалярной функции и сложить их вертикально, чтобы создать якобиан тождественной функции:
Поскольку это функция идентичности, f₁ (Икс) = x₁, f₂ (Икс) = х₂ и тд. Следовательно,
Частичная производная функции по переменной, которой нет в функции, равна нулю. Например, частная производная 2x² по y равна 0. Другими словами,
Поэтому все, что не на диагонали якобиана, становится равным нулю. Между тем, частная производная любой переменной по отношению к себе равна 1. Например, частная производнаяИксв отношенииИксравен 1. Следовательно, якобиан становится:
Градиент комбинаций вектор-векторных функций
Элементарные бинарные операторыявляются операциями (такими как сложениевес+Иксиливес>Икскоторый возвращает вектор единиц и нулей), который применяет оператор последовательно, начиная с первого элемента обоих векторов, чтобы получить первый элемент вывода, затем второго элемента обоих векторов, чтобы получить второй элемент вывода… и так далее.
Эта статья представляет поэлементные бинарные операции с такими обозначениями:
Здесь ◯ означает любой поэлементный оператор (например, +), а не композицию функций.
Итак, как вы находите градиент поэлементной операции двух векторов?
Поскольку у нас есть два набора функций, нам нужны два якобиана, один из которых представляет градиент относительноИкси один по отношению квес:
Большинство арифметических операций нам понадобятся простые, поэтомуе (ш)часто просто векторвес, Другими словами,Fi (Wi) = Wi, Например, операцияW + хподходит к этой категории, так как она может быть представлена каке (ж) + д (х)гдеfi (wi) + gi (xi) = wi + xi.
При этом условии каждый элемент в двух якобианах упрощается до:
На диагонали i = j, поэтому существует значение для частной производной. Вне диагонали, однако, i ≠ j, поэтому частные производные становятся равными нулю:
Мы можем представить это более кратко как:
Попробуем найти градиент функцииW + х, Мы знаем, что все вне диагонали равно 0. Значения частичных по диагонали относительновеса такжеИксявляются:
Давайте попробуем это с умножением:ш * х, Значения частностей по диагонали относительновеса такжеИксявляются:
Следовательно, градиент по отношению квесизш * хявляетсяDiag (Икс)в то время как градиент по отношению кИксизш * хявляетсяDiag (вес).
Применяя те же шаги для вычитания и деления, мы можем суммировать все это:
Градиент векторных сумм
Одной из наиболее распространенных операций в глубоком обучении является операция суммирования. Как мы можем найти градиент функцииу = сумма (Икс)?
у = сумма (Икс)также может быть представлен как:
Следовательно, градиент может быть представлен как:
А так как частная производная функции по переменной, которой нет в функции, равна нулю, ее можно дополнительно упростить следующим образом:
Обратите внимание, что результатом является горизонтальный вектор.
Как насчет градиентау = сумма (Иксг)? Единственное отличие состоит в том, что мы умножаем каждый частный с константой, z:
Хотя это является производной по отношению кИкс, производная по скаляруZэто просто число:
Градиент комбинаций векторных функций правила цепочки
ВЧасть 2мы узнали о правилах цепей с несколькими переменными. Однако это работает только для скаляров. Давайте посмотрим, как мы можем интегрировать это в векторные вычисления!
Давайте возьмем векторную функцию,Yзнак равное(Икс)и найти градиент. Давайте определим функцию как:
И то и другоеf₁ (х)а такжеf₂ (х)являются составными функциями. Введем промежуточные переменные дляf₁ (х)а такжеf₂ (х)и переписать нашу функцию:
Теперь мы можем использовать наше правило цепочки переменных, чтобы вычислить производную вектораY, Просто вычислите производнуюf₁ (х)а такжеf₂ (х)и поместите их один над другим:
Вуаля! У нас есть наш градиент. Однако мы пришли к нашему решению со скалярными правилами, просто сгруппировав числа в вектор. Есть ли способ представить правило цепи с несколькими переменными для векторов?
Прямо сейчас наш градиент вычисляется с помощью:
Обратите внимание, что первый член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₁надИкси второй член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₂надИкс Это как умножение матриц! Поэтому мы можем представить это как:
Давайте проверим наше новое представление правила цепочки векторов:
Мы получаем тот же ответ, что и скалярный подход! Если вместо одного параметраИксу нас есть векторный параметрИкснам просто нужно немного изменить наше правило, чтобы получить полное правило цепочки векторов:
В нашем примере выше,еэто чисто функцияг; то есть,фиявляется функциейсолдатно нетGJ(каждая функцияесоответствует ровно 1 функцииг),В этом случае все вне диагонали становится равным нулю, и:
Теперь у нас есть все части, которые мы находим в градиенте нейронной сети, с которой мы начали нашу серию:
Проверять, выписыватьсяЧасть 4чтобы узнать, как вычислить его производную!
Если вы еще этого не сделали, прочитайте части 1 и 2:
ЧитатьЧасть 4для грандиозного финала!
Скачать оригинал статьиВот,
Если вам понравилась эта статья, не забудьте оставить несколько хлопков! Оставьте комментарий ниже, если у вас есть какие-либо вопросы или предложения 🙂
Градиент заданной функции
Вы будете перенаправлены на Автор24
Определить градиент заданной функции
Решение:
Выражение для градиента находим по формуле
Частные производные имеют вид:
\[\overrightarrow
Готовые работы на аналогичную тему
Определить градиент заданной функции
Решение:
Выражение для градиента в заданной точке находим по формуле
\[\left(\overrightarrow
Частные производные имеют вид:
\[\left(\overrightarrow
Записать уравнение линии уровня в условиях примера 2.
Решение:
Выражение для линии уровня имеет вид:
В условиях примера 2 получаем:
Подставив координаты точки, вычислим значение константы:
Определить градиент заданной функции
Решение:
Выражение для градиента находим по формуле
Частные производные имеют вид:
\[\overrightarrow
Определить градиент заданной функции
Решение:
Выражение для градиента в заданной точке находим по формуле
\[\left(\overrightarrow
Частные производные имеют вид:
\[\left(\overrightarrow
Перечислим некоторые свойства градиента:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 21 04 2021
5.6. Производная по направлению. Градиент. Линии уровня функции
Определение. Предел отношения 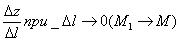
Обозначение.
Если функция F(M) дифференцируема в точке М(х; у), то в точке М(х; у) существует производная по любому направлению L, исходящему из М; вычисляется она по следующей формуле:
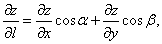
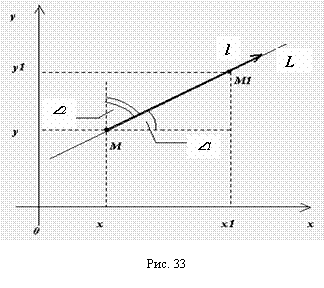
Пример 46. Вычислить производную функции Z=X2+Y2X в точке М(1; 2) по направлению вектора ММ1, где М1 – точка с координатами (3; 0).
Решение. Найдем единичный вектор L, имеющий данное направление:
Откуда Cos=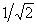
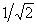
Вычислим частные производные функции в точке М(1; 2):
По формуле (8) получим
Пример 47. Найти производную функции U = Xy2Z3 в точке М(3; 2; 1) В направлении вектора MN, где N(5; 4; 2).
Решение. Найдем вектор 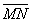
Вычислим значения частных производных в точке М:
Следовательно,
Определение. Градиентом Функции Z=F(M) в точке М(х; у) называется вектор, координаты которого равны соответствующим частным производным 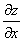
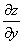
Обозначение.
Пример 49. Найти величину и направление градиента функции 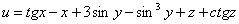
Решение. Найдем частные производные и вычислим их значения в точке М:
Аналогично определяется производная по направлению для функции трех переменных U=F(X, Y, Z), выводятся формулы
Вводится понятие градиента
Подчеркнем, что Основные свойства градиента функции важнее для анализа экономических оптимизационных задач: в направлении градиента функция возрастает. В экономических задачах находят применение следующие свойства градиента:
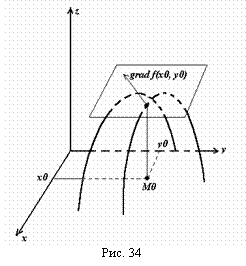
1) Пусть задана функция Z=F(X, Y), имеющая частные производные в области определения. Рассмотрим некоторую точку М0(х0, у0) из области определения. Значение функции в этой точке пусть равно F(X0, Y0). Рассмотрим график функции. Через точку (X0, Y0, F(X0, Y0)) трехмерного пространства проведем плоскость, касательную к поверхности графика функции. Тогда градиент функции, вычисленный в точке (х0, у0), рассматриваемый геометрически как вектор, приложенный в точке (X0, Y0, F(X0, Y0)), будет перпендикулярен касательной плоскости. Геометрическая иллюстрация приведена на рис. 34.
2) Градиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого возрастания функции в точке М0. Кроме того, любое направление, составляющее с градиентом острый угол, является направлением роста функции в точке М0. Другими словами, малое движение из точки (х0, у0) по направлению градиента функции в этой точке ведет к росту функции, причем в наибольшей степени.
Рассмотрим вектор, противоположный градиенту. Он называется Антиградиентом. Координаты этого вектора равны:
Антиградиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого убывания функции в точке М0. Любое направление, образующее острый угол с антиградиентом, является направлением убывания функции в этой точке.
3) При исследовании функции часто возникает необходимость нахождения таких пар (х, у) из области определения функции, при которых функция принимает одинаковые значения. Рассмотрим множество точек (X, Y) из области определения функции F(X, Y), таких, что F(X, Y)=Const, где запись “Const” означает, что значение функции зафиксировано и равно некоторому числу из области значений функции.
Определение. Множество линий уровня называют Картой линий уровня.
Хорошо известны примеры линий уровня – уровни одинаковых высот на топографической карте и линии одинакового барометрического давления на карте погоды.
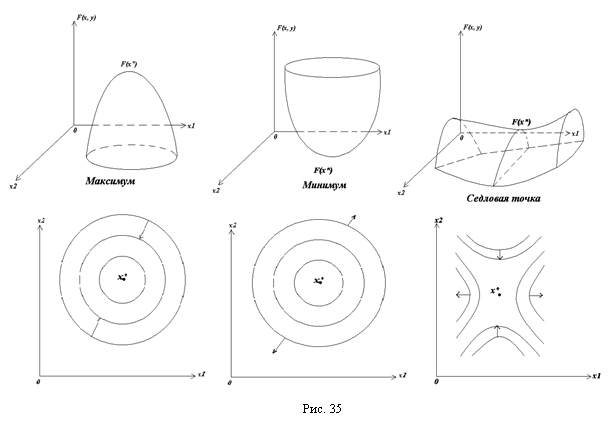
Определение. Направление, вдоль которого скорость увеличения функции максимальна, называется «предпочтительным» направлением, или Направлением наискорейшего роста.
«Предпочтительное» направление задается вектором-градиентом функции. На рис. 35 изображены максимум, минимум и седловая точка в задаче оптимизации функции двух переменных при отсутствии ограничений. В нижней части рисунка изображены линии уровня и направления наискорейшего роста.
Решение. Уравнение семейства линий уровня имеет вид X2+Y2=C (C>0). Придавая С различные действительные значения, получим концентрические окружности с центром в начале координат.
Пример 51. Рассмотрим следующую экономическую ситуацию. Пусть производство продукции описывается Функцией Кобба-Дугласа F(X, Y)=10х1/3у2/3, где Х – количество труда, У – количество капитала. На приобретение ресурсов выделено 30 у. ед., цена труда составляет 5 у. ед., капитала – 10 у. ед. Зададимся вопросом: какой наибольший выпуск можно получить в данных условиях? Здесь под «данными условиями» имеются в виду заданные технологии, цены на ресурсы, вид производственной функции. Как уже отмечалось, функция Кобба-Дугласа является монотонно возрастающей по каждой переменной, т. е. увеличение каждого вида ресурса ведет к росту выпуска. В данных условиях ясно, что увеличивать приобретение ресурсов можно до тех пор, пока хватает денег. Наборы ресурсов, стоимость которых составляет 30 у. ед., удовлетворяют условию:
Т. е. определяют линию уровня функции:
С другой стороны, с помощью линий уровня Функции Кобба-Дугласа (рис. 36) можно показать возрастание функции: в любой точке линии уровня направление градиента – это направление наибольшего возрастания, а для построения градиента в точке достаточно провести касательную к линии уровня в этой точке, построить перпендикуляр к касательной и указать направление градиента. Из рис. 36 видно, что движение линии уровня функции Кобба-Дугласа вдоль градиента следует производить до тех пор, пока она не станет касательной к линии уровня 5х + 10у = 30. Таким образом, с помощью понятий линии уровня, градиента, свойств градиента можно выработать подходы к наилучшему использованию ресурсов с точки зрения увеличения объемов выпускаемой продукции.