Что показывает коэффициент б в квадратичной функции

Как определить a, b и c по графику параболы

Предположим, вам попался график функции \(y=ax^2+bx+c\) и нужно по этому графику определить коэффициенты \(a\), \(b\) и \(c\). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью \(y\) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент \(a\) можно найти с помощью следующих фактов:

— Если \(a>0\), то ветви параболы направленных вверх, если \(a 1\), то график вытянут вверх в \(a\) раз по сравнению с «базовым» графиком (у которого \(a=1\)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: \(y=ax^2+bx+c\). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим \(9a\) вместо \(b\):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки \(A\) и \(B\) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение \(a\):

Получается квадратичная функция: \(y=-x^2-9x-15\).

Сразу заметим, что по графику можно сразу определить, что \(c=4\). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: \(C(-1;8)\), \(D(1;2)\) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Сам способ базируется на следующих идеях:

График \(y=-x^2\) симметричен относительно оси \(x\) графику \(y=x^2\).

– Если \(a>1\) график \(y=ax^2\) получается растяжением графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.
– Если \(a∈(0;1)\) график \(y=ax^2\) получается сжатием графика \(y=x^2\) вдоль оси \(y\) в \(a\) раз.

– График \(y=a(x+d)^2\) получается сдвигом графика \(y=ax^2\) влево на \(d\) единиц.
— График \(y=a(x-d)^2\) получается сдвигом графика \(y=ax^2\) вправо на \(d\) единиц.

График \(y=a(x+d)^2+e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вверх.
График \(y=a(x+d)^2-e\) получается переносом графика \(y=a(x+d)^2\) на \(e\) единиц вниз.

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому \(a=1\). То есть она получена перемещениями графика базовой параболы \(y=x^2\).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на \(4\).

То есть наша функция выглядит так: \(y=(x-5)^2-4\).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти \(f(6)\), надо сначала узнать формулу функции \(f(x)\). Найдем её:

Парабола растянута на \(2\) и ветви направлены вниз, поэтому \(a=-2\). Иными словами, первоначальной, перемещаемой функцией является функция \(y=-2x^2\).

Парабола смещена на 2 клеточки вправо, поэтому \(y=-2(x-2)^2\).

Парабола поднята на 4 клеточки вверх, поэтому \(y=-2(x-2)^2+4\).

Источник

Что показывает коэффициент б в квадратичной функции

Задания на свойства и графики квадратичной функции вызывают, как показывает практика, серьезные затруднения. Это довольно странно, ибо квадратичную функцию проходят в 8 классе, а потом всю первую четверть 9-го класса «вымучивают» свойства параболы и строят ее графики для различных параметров.

Это связано с тем, что заставляя учащихся строить параболы, практически не уделяют времени на «чтение» графиков, то есть не практикуют осмысление информации, полученной с картинки. Видимо, предполагается, что, построив десятка два графиков, сообразительный школьник сам обнаружит и сформулирует связь коэффициентов в формуле и внешний вид графика. На практике так не получается. Для подобного обобщения необходим серьезный опыт математических мини исследований, которым большинство девятиклассников, конечно, не обладает. А между тем, в ГИА предлагают именно по графику определить знаки коэффициентов.

Не будем требовать от школьников невозможного и просто предложим один из алгоритмов решения подобных задач.

Посмотрим, как влияют на внешний вид параболы знаки ее коэффициентов.

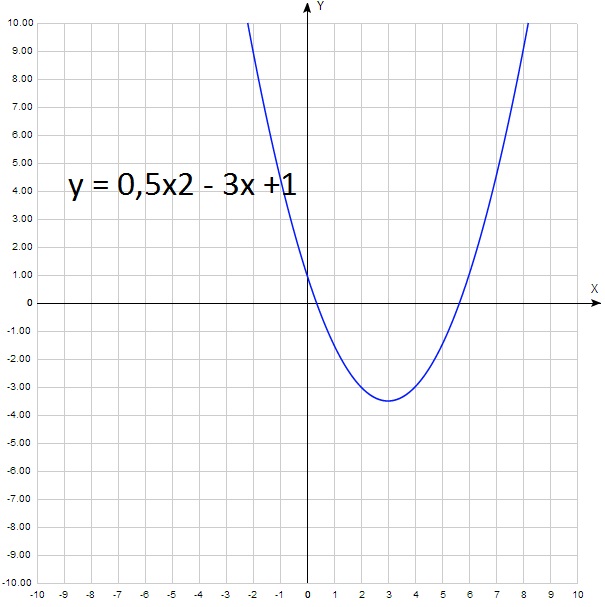
Самая простая зависимость для коэффициента а. Большинство школьников уверенно отвечает: » если а > 0, то ветви параболы направлены вверх, а если а 0.

В данном случае а = 0,5

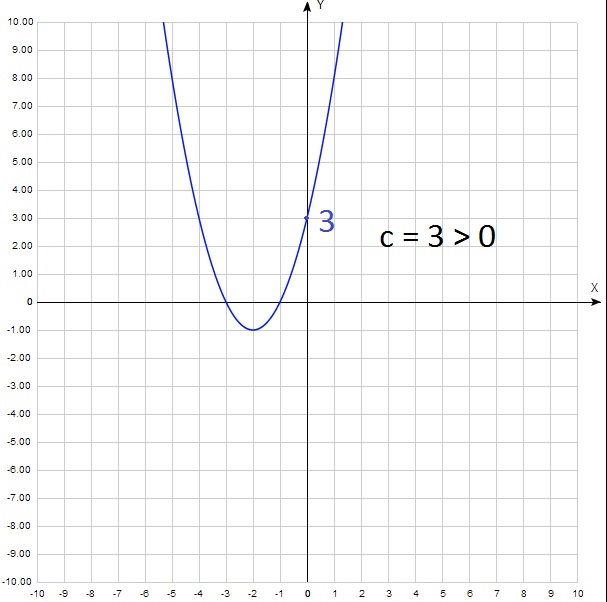
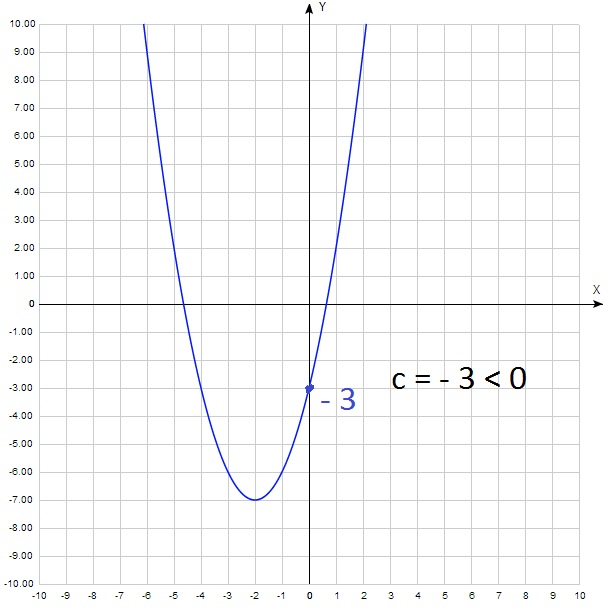
А теперь для а 2 + b 0 + c = c. Получается, что у = с. То есть с – это ордината точки пересечения параболы с осью у. Как правило, эту точку легко найти на графике. И определить выше нуля она лежит или ниже. То есть с > 0 или с 0:

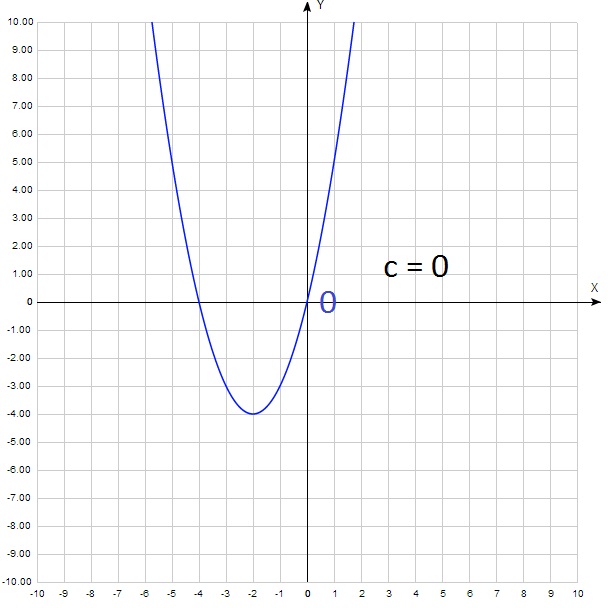
Соответственно, если с = 0, то парабола обязательно будет проходить через начало координат:

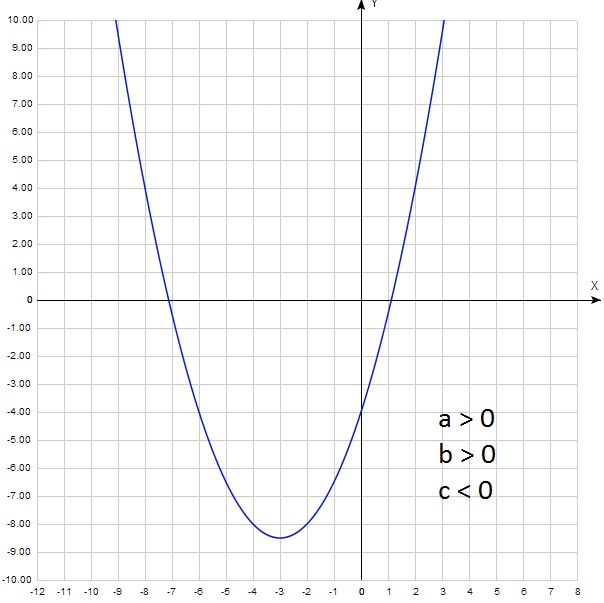
Ветви направлены вверх, значит а > 0, парабола пересекает ось у ниже нуля, значит с 0. Окончательно имеем: а > 0, b > 0, с 0)

тел. моб. (495) 642 42 50. Звонить можно до 23:00.

тел. моб. 8 (499) 723 68 84. Звонить можно до 23:00.

тел. дом. 8 (925) 642 42 50. Звонить можно до 23:00.

Источник

Парабола, график, вершина, нули.

теория по математике 📈 функции

Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.

Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax 2 +bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х 2 +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

D=b 2 – 4ac=4 2 — 4 ∙ 1 ∙ ( − 5 ) = 36

Значит, нули функции равны –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

А) a>0, с >0 Б) а 0 В) а>0, с

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 — это график №1

Б) а 0 — это график №3

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

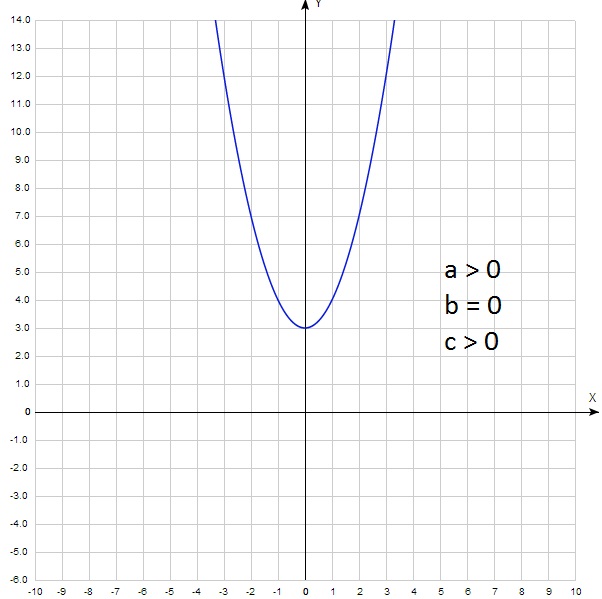
Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

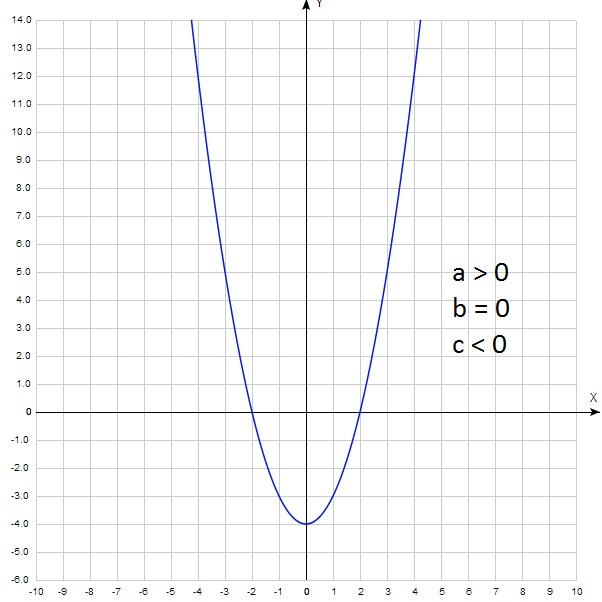
Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3

pазбирался: Даниил Романович | обсудить разбор | оценить

На рисунках изображены графики функций вида

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

Из всего вышеперечисленного можно найти ответ:

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

У р о к 15.
Влияние коэффициентов а, b и с на расположение
графика квадратичной функции

Цели: продолжить формирование умения строить график квадратичной функции и перечислять ее свойства; выявить влияние коэффициентов а, b и с на расположение графика квадратичной функции.

I. Организационный момент.

Определите, график какой функции изображен на рисунке:

б)

у = х 2 – 2х;

у = – х 2 + 4х + 1;

у = – х 2 + 2х – 1.

III. Формирование умений и навыков.

Прямая у = 6х + b касается параболы у = х 2 + 8, то есть имеет с ней только одну общую точку в том случае, когда уравнение 6х + b = х 2 + 8 будет иметь единственное решение.

Это уравнение является квадратным, найдем его дискриминант:

3. Выявить влияние коэффициентов а, b и с на расположение графика функции у = ах 2 + bх + с.

Учащиеся обладают достаточными знаниями, чтобы выполнить это задание самостоятельно. Следует предложить им все полученные выводы занести в тетрадь, при этом выделив «основную» роль каждого из коэффициентов.

1) Коэффициент а влияет на направление ветвей параболы: при а > 0 – ветви направлены вверх, при а , так как а 0.

4. Определите, график какой функции изображен на рисунке, опираясь на значение коэффициентов а, b и с.

у = х 2 + 2х + 2;

По изображенному графику делаем следующие выводы о коэффициентах а, b и с:

а > 0, так как ветви параболы направлены вверх;

b ≠ 0, так как вершина параболы не лежит на оси ОУ;

с = –2, так как парабола пересекает ось ординат в точке (0; –2).

Всем этим условиям удовлетворяет только функция у = 2х 2 – 3х – 2.

По изображенному графику делаем следующие выводы о коэффициентах а, b и с:

5. По графику функции у = ах 2 + bх + с определите знаки коэффициентов а, b и с:

а) б)

а) Ветви параболы направлены вверх, поэтому а > 0.

Парабола пересекает ось ординат в нижней полуплоскости, поэтому с . По графику видно, что т 0. Поэтому b > 0.

б) Аналогично определяем знаки коэффициентов а, b и с:

а) По теореме Виета, известно, что если х₁ и х₂ – корни уравнения х 2 +
+ рх + q = 0 (то есть нули данной функции), то х₁ · х₂ = q и х₁ + х₂ = –р. Получаем, что q = 3 · 4 = 12 и р = –(3 + 4) = –7.

б) Точка пересечения параболы с осью ОУ даст значение параметра q, то есть q = 6. Если график функции пересекает ось ОХ в точке (2; 0), то число 2 является корнем уравнения х 2 + рх + q = 0. Подставляя значение х = 2 в это уравнение, получим, что р = –5.

в) Своего наименьшего значения данная квадратичная функция достигает в вершине параболы, поэтому , откуда р = –12. По условию значение функции у = х 2 – 12х + q в точке x = 6 равно 24. Подставляя x = 6 и у = 24 в данную функцию, находим, что q = 60.

IV. Проверочная работа.

1. Постройте график функции у = 2х 2 + 4х – 6 и найдите, используя график:

б) промежутки, в которых у > 0 и y 2 + 4х, найдите:

б) промежутки возрастания и убывания функции;

в) область значения функции.

3. По графику функции у = ах 2 + bх + с определите знаки коэффициентов а, b и с:

1. Постройте график функции у = –х 2 + 2х + 3 и найдите, используя график:

б) промежутки, в которых у > 0 и y 2 + 8х, найдите:

б) промежутки возрастания и убывания функции;

в) область значения функции.

3. По графику функции у = ах 2 + bх + с определите знаки коэффициентов а, b и с:

В о п р о с ы у ч а щ и м с я:

– Опишите алгоритм построения квадратичной функции.

– Перечислите свойства функции у = ах 2 + bх + с при а > 0 и при а

Источник

Квадратичная функция. Построение параболы

8 класс, 9 класс, ЕГЭ/ОГЭ

Основные понятия

Функция — это зависимость «y» от «x», при которой «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.

Задать функцию означает определить правило в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

График функции — это объединение всех точек, когда вместо «x» можно подставить в функцию произвольные значения и найти координаты этих точек.

Еще быстрее разобраться в теме и научиться строить график квадратичной функции можно на курсах по математике в онлайн-школе Skysmart.

Построение квадратичной функции

Квадратичная функция задается формулой y = ax 2 + bx + c, где x и y — переменные, a, b, c — заданные числа, обязательное условие — a ≠ 0. В уравнении существует следующее распределение:

График квадратичной функции — парабола, которая имеет следующий вид для y = x 2 :

Если в уравнении квадратичной функции старший коэффициент равен единице, то график имеет ту же форму, как y = x 2 при любых значениях остальных коэффициентов.

График функции y = –x 2 выглядит, как перевернутая парабола:

Зафиксируем координаты базовых точек в таблице:

Посмотрев на оба графика можно заметить их симметричность относительно оси ОХ. Отметим важные выводы:

Рассмотрим три случая:

Если a > 0, то график выглядит как-то так:

0″ height=»671″ src=»https://lh6.googleusercontent.com/8ryBuyxmK9S2EbnsNc4AE5PEl_NpIg0RAM_Y_V8wUP-zREEHNgi9QoQTl8FXxoujjWRAvf3s-MPRsXsoepaLLSTHDX-ReGtrsnLQp4dW3WaEyPF2ywjVpYFXlDIpAEHoIiwlxiB7″ width=»602″>

На основе вышеизложенного ясно, что зная направление ветвей параболы и знак дискриминанта, у нас есть понимание, как будет выглядеть график конкретной функции.

Координаты вершины параболы также являются важным параметром графика квадратичной функции и находятся следующим способом:

Ось симметрии параболы — прямая, которая проходит через вершину параболы параллельно оси OY.

Чтобы построить график, нам нужна точка пересечения параболы с осью OY. Так как абсцисса каждой точки оси OY равна нулю, чтобы найти точку пересечения параболы y = ax 2 + bx + c с осью OY, нужно в уравнение вместо х подставить ноль: y(0) = c. То есть координаты этой точки будут соответствовать: (0; c).

На изображении отмечены основные параметры графика квадратичной функции:

Алгоритм построения параболы

Рассмотрим несколько способов построения квадратичной параболы. Наиболее удобный способ можно выбрать в соответствии с тем, как задана квадратичная функция.

Уравнение квадратичной функции имеет вид y = ax 2 + bx + c.

Как строим:

В данном случае дискриминант больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ. Чтобы найти их координаты, решим уравнение:

Как строим:

Уравнение квадратичной функции имеет вид y = (x + a) × (x + b)

Рассмотрим следующий пример: y = (x − 2) × (x + 1).

Как строим:

Данный вид уравнения позволяет быстро найти нули функции:

(x − 2) × (x + 1) = 0, отсюда х₁ = 2, х₂ = −1.

Определим координаты вершины параболы:

Найти точку пересечения с осью OY:

с = ab = (−2) × (1) = −2 и ей симметричная.

Отметим эти точки на координатной плоскости и соединим плавной прямой.

Источник