Что показывает модуль вектора ускорения кратко

Ускорение в кинематике формула. Ускорение в кинематике определение

Ускорение в кинематике формула. Ускорение в кинематике определение.

Что такое ускорение?

Скорость может изменяться во время движения.

Скорость является векторной величиной.

Вектор скорости может изменяться по направлению и по модулю, т.е. по величине. Для учёта таких изменений скорости используют ускорение.

Ускорение определение

Ускорение, его ещё называют полным ускорением, является вектором.

Вектор ускорения

Вектор ускорения есть сумма двух других векторов. Один из этих других векторов называется тангенциальным ускорением, а другой называется нормальным ускорением.

Тангенциальное ускорение описывает изменение модуля вектора скорости.

Нормальное ускорение описывает изменение направления вектора скорости.

При прямолинейном движении направление скорости не меняется. В этом случае нормальное ускорение равно нулю, а полное и тангенциальное ускорения совпадают.

При равномерном движении модуль скорости не меняется. В этом случае тангенциальное ускорение равно нулю, а полное и нормальное ускорения совпадают.

Если тело совершает прямолинейное равномерное движение, то его ускорение равно нулю. А это значит, что и составляющие полного ускорения, т.е. нормальное ускорение и тангенциальное ускорение, тоже равны нулю.

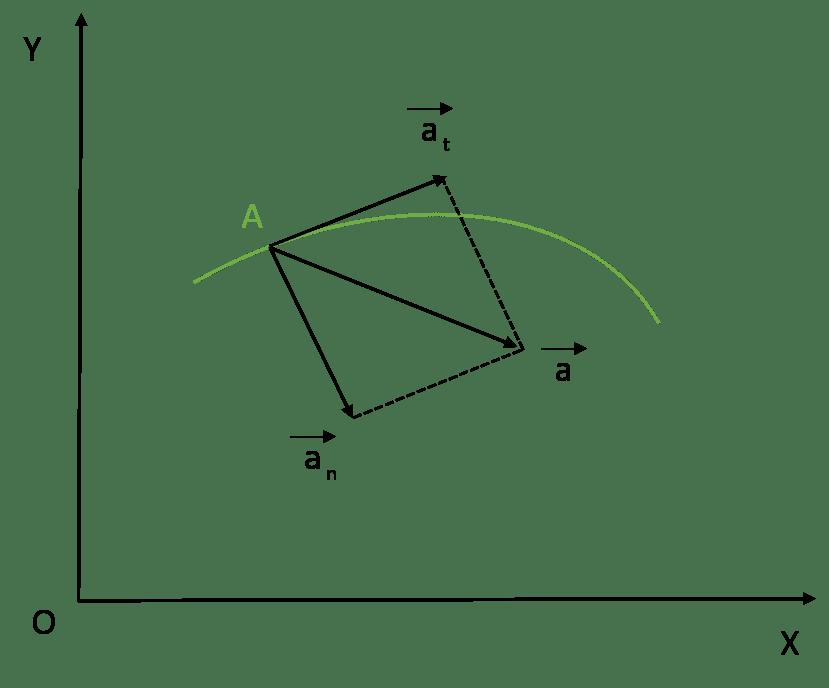
Вектор полного ускорения

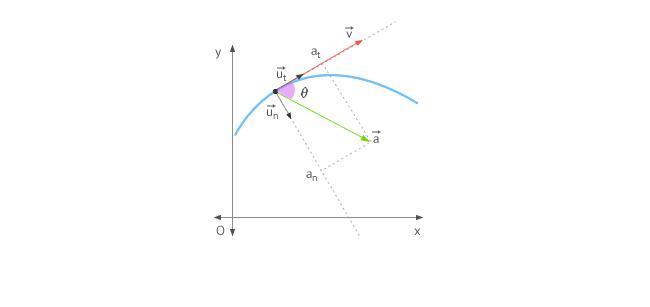
Вектор полного ускорения равен геометрической сумме нормального и тангенциального ускорений, как показано на рисунке:

Модуль полного ускорения

Модуль полного ускорения:

Угол альфа между вектором полного ускорения и нормальным ускорением (он же угол между вектором полного ускорения и радиус-вектором):

Обратите внимание, что вектор полного ускорения не направлен по касательной к траектории.

По касательной направлен вектор тангенциального ускорения.

Направление вектора полного ускорения определяется векторной суммой векторов нормального и тангенциального ускорений.

Источник

Векторы ускорения и скорости. Ускорение и сила. Направления тангенциального и нормального ускорений

Как известно, любая физическая величина относится к одному из двух типов, она является либо скалярной, либо векторной. В данной статье рассмотрим такие кинематические характеристики как скорость и ускорение, а также покажем, куда направлены векторы ускорения и скорости.

Что такое скорость и ускорение?

Обе величины, названные в этом пункте, являются важными характеристиками любого вида движения, будь то перемещение тела по прямой линии или по криволинейной траектории.

Вам будет интересно: Дистанционное образование в России: история, статистика и преимущества

Скоростью называется быстрота изменения координат во времени. Математически эта величина равна производной по времени пройденного пути, то есть:

Здесь вектор l¯ направлен от начальной точки пути к конечной.

В свою очередь ускорение – это скорость, с которой изменяется во времени сама скорость. В виде формулы оно может быть записано так:

Очевидно, что взяв вторую производную от вектора перемещения l¯ по времени, мы также получим значение ускорения.

Поскольку скорость измеряется в метрах в секунду, то ускорение, согласно записанному выражению, измеряется в метрах в секунду в квадрате.

Куда направлены векторы ускорения и скорости?

Вектор скорости тела направлен в сторону движения всегда, независимо от того, замедляется или ускоряется тело, движется оно по прямой или по кривой. Если говорить геометрическими терминами, то вектор скорости направлен по касательной к точке траектории, в которой в данный момент находится тело.

Вектор ускорения точки материальной или тела не имеет ничего общего со скоростью. Этот вектор направлен в сторону изменения скорости. Например, для прямолинейного движения величина a¯ может как совпадать по направлению с v¯, так и быть противоположной v¯.

Действующая на тело сила и ускорение

Мы выяснили, что вектор ускорения тела направлен в сторону изменения вектора скорости. Тем не менее не всегда можно легко определить, как меняется скорость в данной точке траектории. Более того, для определения изменения скорости необходимо выполнить операцию разности векторов. Чтобы избежать этих трудностей в определении направления вектора a¯, существует еще один способ быстро его узнать.

Ниже записан знаменитый и хорошо известный каждому школьнику закон Ньютона:

Формула показывает, что причиной возникновения ускорения у тел является действующая на них сила. Поскольку масса m является скаляром, то вектор силы F¯ и вектор ускорения a¯ направлены одинаково. Этот факт следует запомнить и применять на практике всегда, когда возникает необходимость в определении направления величины a¯.

Если на тело действуют несколько разных сил, тогда направление вектора ускорения будет равно результирующему вектору всех сил.

Движение по окружности и ускорение

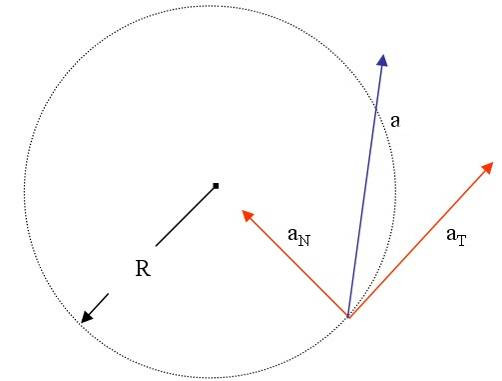
Когда тело перемещается по прямой линии, то ускорение направлено либо вперед, либо назад. В случае же движения по окружности ситуация усложняется тем, что вектор скорости постоянно меняет свое направление. В виду сказанного, полное ускорение определяется двумя его составляющими: тангенциальным и нормальным ускорениями.

Тангенциальное ускорение направлено точно так же, как вектор скорости, или против него. Иными словами, эта компонента ускорения направлена вдоль касательной к траектории. Ускорение тангенциальное описывает изменение модуля самой скорости.

Ускорение нормальное направлено вдоль нормали к данной точке траектории с учетом ее кривизны. В случае движения по окружности вектор этой компоненты указывает на центр, то есть нормальное ускорение направлено вдоль радиуса вращения. Эту компоненту часто называют центростремительной.

Полное ускорение представляет собой сумму названных компонент, поэтому его вектор может быть направлен произвольным образом по отношению к линии окружности.

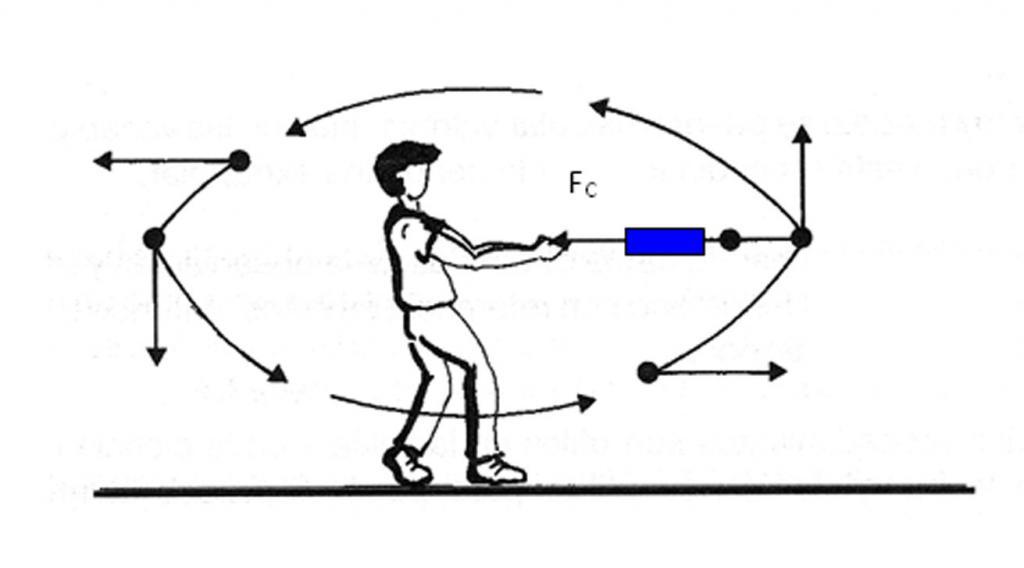
Если тело совершает вращение без изменения линейной скорости, то существует отличная от нуля только нормальная компонента, поэтому вектор полного ускорения направлен к центру окружности. Заметим, что к этому центру также действует сила, удерживающая тело на его траектории. Например, сила гравитации Солнца удерживает нашу Землю и другие планеты на своих орбитах.

Источник

Формулы модуля ускорения для прямолинейного и криволинейного движения. Пример решения задачи

В физике существует несколько видов ускорения, которые используются для описания того или иного типа механического перемещения тел в пространстве. Все эти виды являются векторными величинами. В данной статье не будем рассматривать вопрос, куда направлено ускорение, а сосредоточим свое внимание на формулах модуля ускорения.

Что такое ускорение?

Вам будет интересно: Смоленский государственный институт искусств: факультеты, специальности, сроки обучения, документы для поступления

Оно называется мгновенным, то есть справедливым для конкретного момента времени t. Чтобы найти среднее значение модуля ускорения, формулу такую необходимо использовать:

Единицами измерения изучаемой физической величины являются метры в квадратную секунду (м/с2). Многих может смутить возведение во вторую степень единиц времени, тем не менее, понять смысл единицы м/с2 несложно, если ее представить в виде [м/с]/с. Последняя запись означает изменение скорости на одну единицу за одну единицу времени.

Движение по прямой и ускорение

Самой простой траекторией для перемещения тел в пространстве является прямая линия. Если скорость при движении по такой траектории не изменяется, то говорить об ускорении не приходится, поскольку оно будет равно нулю.

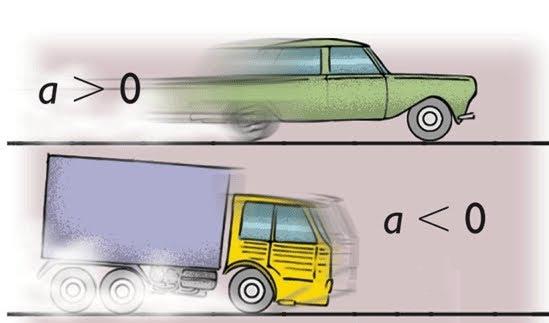
В технике широко распространено прямолинейное равноускоренное (равнозамедленное) движение. Например, при старте автомобиля или при его торможении мы имеем именно этот вид движения. Для его математического описания пользуются следующими равенствами:

Как правило, если тело ускоряется, то говорят о положительном ускорении, если же оно замедляет свое движение, то говорят об отрицательной величине a. Нетрудно проверить, что обе формулы приводят к одной и той же единице измерения ускорения (м/с2).

Полное ускорение и его компоненты при движении тела по кривой

В случае перемещения тела по криволинейной траектории, величину a удобно представить в виде двух взаимно перпендикулярных составляющих. Они называются тангенциальным at и нормальным an ускорениями. Для такого случая формула модуля ускорения точки принимает вид:

Тангенциальную компоненту следует рассчитывать через производную функции v(t) по времени. Нормальная же компонента определяется не изменением модуля скорости, а самой ее величиной. Для ее расчета пользуются таким выражением:

Для полноты информации отметим, что криволинейность траектории перемещения тела является достаточным признаком присутствия ненулевой нормальной составляющей ускорения. При этом величина at может быть равна нулю, что является справедливым для равномерного вращения тел.

Угловое ускорение

Как было отмечено во введении, существуют несколько видов ускорения. Одним из них является угловая кинематическая величина. Обозначим ее α. По аналогии с линейным ускорением, формула модуля ускорения углового имеет вид:

Где греческой буквой ω (омега) обозначена скорость угловая, единицами измерения которой являются радианы в секунду. Величина α показывает, как быстро тело увеличивает или замедляет скорость своего вращения.

Ускорение угловое можно связать с линейной величиной. Делается это с помощью такой формулы:

Важно понимать, что угловое ускорение является удобным способом представления тангенциальной составляющей полного ускорения в случае вращательного движения. Удобство здесь заключается в независимости величины α от расстояния до оси вращения r. В свою очередь, компонента at линейно возрастает при увеличении радиуса кривизны r.

Пример решения задачи

Известно, что тело вращается по окружности, радиус которой составляет 0,2 метра. Вращение является ускоренным, при этом скорость изменяется во времени по следующему закону:

Необходимо определить тангенциальное, нормальное, полное и угловое ускорения в момент времени 3 секунды.

Начнем решать эту задачу по порядку. Тангенциальная компонента определяется через производную скорости. Имеем:

at = dv/dt = 6*t + 6*t2 = 6*3 + 6*9 = 76 м/с2.

Отметим, что это очень большое ускорение по сравнению с ускорением свободного падения (9,81 м/с2).

Нормальная компонента вычисляется так:

an = v2/r = 1/r*(2 + 3*t2 + 2*t3)2 = 1/0,2*(2+27+54)2 = 34445 м/c2.

Теперь можно рассчитать полное ускорение. Оно будет равно:

a = √(at2 + an2) = √(76 2 + 34445 2) = 34445,1 м/с2.

То есть, полное ускорение практически полностью образовано нормальной компонентой.

Наконец, ускорение угловое определяется по формуле:

α = at/r = 76/0,2 = 380 рад/с2.

Полученное значение соответствует увеличению скорости угловой приблизительно на 60 оборотов за каждую секунду.

Источник

9 класс

§ 5. Прямолинейное равноускоренное движение. Ускорение

В 7 классе вы изучали механическое движение тел, происходящее с постоянной скоростью, т. е. равномерное движение.

Теперь мы переходим к рассмотрению неравномерного движения. Из всех видов неравномерного движения мы будем изучать самое простое — прямолинейное равноускоренное, при котором тело движется вдоль прямой линии, а проекция вектора скорости тела за любые равные промежутки времени меняется одинаково (при этом модуль вектора скорости может как увеличиваться, так и уменьшаться).

Например, если скорость движущегося по взлётной полосе самолёта за любые 10 c увеличивается на 15 м/с, за любые 5 с — на 7,5 м/с, в каждую секунду — на 1,5 м/с и т. д., то самолёт движется равноускоренно.

В данном случае под скоростью движения самолёта подразумевается его так называемая мгновенная скорость, т. е. скорость в каждой конкретной точке траектории в соответствующий момент времени (более строгое определение мгновенной скорости будет дано в курсе физики старших классов).

Мгновенная скорость тел, движущихся равноускоренно, может меняться по-разному: в одних случаях быстрее, в других — медленнее. Например, скорость обычного пассажирского лифта средней мощности за каждую секунду разгона увеличивается на 0,4 м/с, а скоростного — на 1,2 м/с. В таких случаях говорят, что тела движутся с разным ускорением.

Рассмотрим, какая физическая величина называется ускорением.

Пусть скорость некоторого тела, движущегося равноускоренно, за промежуток времени t изменилась от ν₀ до ν. Под ν₀ подразумевается начальная скорость тела, т. е. скорость в момент t₀ = 0, принятый за начало отсчёта времени. A ν — это скорость, которую тело имело к концу промежутка времени t, отсчитываемого от t₀ = 0. Тогда за каждую единицу времени скорость менялась на величину, равную .

Это отношение обозначается символом и называется ускорением:

Ускорением тела при прямолинейном равноускоренном движении называется векторная физическая величина, равная отношению изменения скорости к промежутку времени, за который это изменение произошло.

Равноускоренное движение — это движение с постоянным ускорением.

Ускорение — векторная величина, которая характеризуется не только модулем, но и направлением.

Модуль вектора ускорения показывает, на сколько меняется модуль вектора скорости в каждую единицу времени. Чем больше ускорение, тем быстрее меняется скорость тела.

За единицу ускорения в СИ принимается ускорение такого равноускоренного движения, при котором за 1 с скорость тела изменяется на 1 м/с:

Таким образом, в СИ единицей ускорения является метр на секунду в квадрате (м/с 2 ).

Вычислить ускорение тела, движущегося прямолинейно и равноускоренно, можно с помощью следующего уравнения, в которое входят проекции векторов ускорения и скорости:

Покажем на конкретных примерах, как находится ускорение.

На рисунке 8, а изображены санки, которые равноускоренно скатываются с горы.

Известно, что участок пути AB санки прошли за 4 с. При этом в точке А они имели скорость, равную 0,4 м/с, а в точке В — скорость, равную 2 м/с (санки приняты за материальную точку).

Определим, с каким ускорением двигались санки на участке АВ.

В данном случае за начало отсчёта времени следует принять момент прохождения санками точки А, поскольку согласно условию именно от этого момента отсчитывается промежуток времени, за который модуль вектора скорости изменился от 0,4 до 2 м/с.

Теперь проведём ось X, параллельную вектору скорости движения санок и направленную в ту же сторону. Спроецируем на неё начала и концы векторов ₀ и . Образовавшиеся при этом отрезки v_0x и v_x являются проекциями векторов ₀ и на ось X. Обе эти проекции положительны и равны модулям соответствующих векторов: v_0x = 0,4 м/с, v_x = 2 м/с.

Запишем условие задачи и решим её.

Проекция вектора ускорения на ось X получилась положительной, значит, вектор ускорения сонаправлен с осью X и со скоростью движения санок.

Если векторы скорости и ускорения направлены в одну сторону, то скорость растёт.

Теперь рассмотрим другой пример, в котором санки, скатившись с горы, движутся по горизонтальному участку CD (рис. 8, б).

В результате действия на санки силы трения их скорость непрерывно уменьшается, и в точке D санки останавливаются, т. е. их скорость равна нулю. Известно, что в точке C санки имели скорость 1,2 м/с, а участок CD был пройден ими за 6 с.

Рассчитаем ускорение санок в этом случае, т. е. определим, на сколько менялась скорость санок за каждую единицу времени.

Началом отсчёта времени будем считать момент, когда санки проходят точку С. Тогда модуль вектора начальной скорости равен 1,2 м/с, а конечной — нулю.

Проведём ось X параллельно отрезку CD и сонаправим её со скоростью движения санок, как показано на рисунке. При этом проекция вектора скорости санок на ось X в любой момент их движения будет положительна и равна модулю вектора скорости. В частности, при t₀ = 0 υ_0x = 1,2 м/с, а при t = 6 с υ_x = 0.

Запишем данные и вычислим ускорение.

Проекция ускорения на ось X отрицательна. Это значит, что вектор ускорения а направлен противоположно оси X и соответственно противоположно скорости движения. При этом скорость санок уменьшалась.

Таким образом, если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости тела увеличивается, а если в противоположные — уменьшается.

Вопросы:

1. К какому виду движения — равномерному или неравномерному — относится прямолинейное равноускоренное движение?

2. Что понимают под мгновенной скоростью неравномерного движения?

3. Дайте определение ускорения равноускоренного движения. Какова единица ускорения?

4. Что такое равноускоренное движение?

5. Что показывает модуль вектора ускорения?

6. При каком условии модуль вектора скорости движущегося тела увеличивается; уменьшается?

Упражнения:

Упражнение № 5

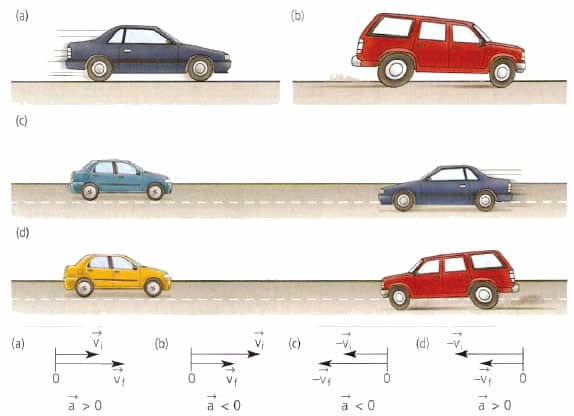
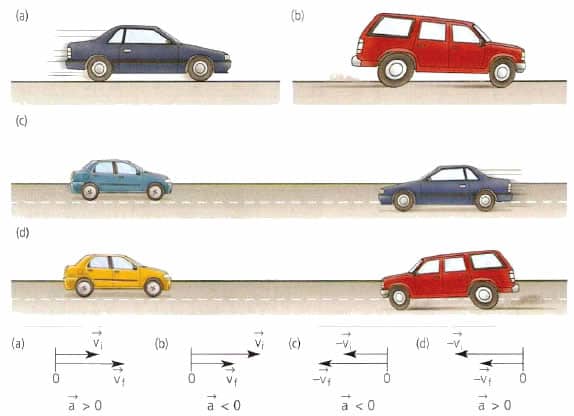
1. За один и тот же промежуток времени t модуль вектора скорости первого автомобиля изменился от υ₁ до υ’, а второго — от υ₂ до υ’ (векторы скорости изображены в одинаковом масштабе на рисунке 9). Какой из автомобилей двигался в указанный промежуток с большим ускорением? Скорость какого из них возрастала быстрее?

2. Самолёт, разгоняясь перед взлётом, в течение некоторого промежутка времени двигался равноускоренно. Каково было при этом ускорение самолёта, если за 30 с его скорость возросла от 10 до 55 м/с?

3. C каким ускорением двигался поезд на некотором участке пути, если за 12 с его скорость возросла на 6 м/с?

Источник

Основы механики для чайников. Часть 1: Кинематика

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник