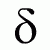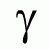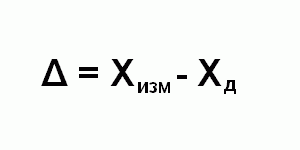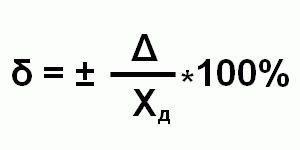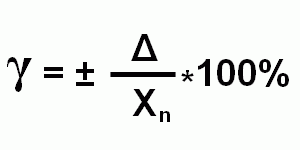Что показывает полученная в работе относительная погрешность
Относительная погрешность
Погре́шность измере́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения.
Поскольку выяснить с абсолютной точностью истинное значение любой величины невозможно, то невозможно и указать величину отклонения измеренного значения от истинного. (Это отклонение принято называть ошибкой измерения. В ряде источников, например, в БСЭ, термины ошибка измерения и погрешность измерения используются как синонимы.) Возможно лишь оценить величину этого отклонения, например, при помощи статистических методов. При этом за истинное значение принимается среднестатистическое значение, полученное при статистической обработке результатов серии измерений. Это полученное значение не является точным, а лишь наиболее вероятным. Поэтому в измерениях необходимо указывать, какова их точность. Для этого вместе с полученным результатом указывается погрешность измерений. Например, запись T=2.8±0.1 c. означает, что истинное значение величины T лежит в интервале от 2.7 с. до 2.9 с. некоторой оговоренной вероятностью (см. доверительный интервал, доверительная вероятность, стандартная ошибка).
В 2006 году на международном уровне был принят новый документ, диктующий условия проведения измерений и установивший новые правила сличения государственных эталонов. Понятие «погрешность» стало устаревать, вместо него было введено понятие «неопределенность измерений».
Содержание
Определение погрешности
В зависимости от характеристик измеряемой величины для определения погрешности измерений используют различные методы.
Классификация погрешностей
По форме представления
где Xtrue — истинное значение, а Xmeas — измеренное значение, должно выполняться с некоторой вероятностью близкой к 1. Если случайная величина Xmeas распределена по нормальному закону, то, обычно, за абсолютную погрешность принимают её среднеквадратичное отклонение. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина.

Относительная погрешность является безразмерной величиной, либо измеряется в процентах.
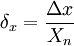
— если шкала прибора односторонняя, т.е. нижний предел измерений равен нулю, то Xn определяется равным верхнему пределу измерений;
— если шкала прибора двухсторонняя, то нормирующее значение равно ширине диапазона измерений прибора.
По причине возникновения
В технике применяют приборы для измерения лишь с определенной заранее заданной точностью – основной погрешностью, допускаемой нормали в нормальных условиях эксплуатации для данного прибора.
Если прибор работает в условиях, отличных от нормальных, то возникает дополнительная погрешность, увеличивающая общую погрешность прибора. К дополнительным погрешностям относятся: температурная, вызванная отклонением температуры окружающей среды от нормальной, установочная, обусловленная отклонением положения прибора от нормального рабочего положения, и т.п. За нормальную температуру окружающего воздуха принимают 20°С, за нормальное атмосферное давление 01,325 кПа.
Погрешности измерений, представление результатов эксперимента
п.1. Шкала измерительного прибора
Примеры шкал различных приборов:
 Манометр – прибор для измерения давления, круговая шкала |  Вольтметр – прибор для измерения напряжения, дуговая шкала |  Индикатор громкости звука, линейная шкала |
п.2. Цена деления
Пример определения цены деления:
 | Определим цену деления основной шкалы секундомера. Два ближайших пронумерованных деления на основной шкале: a = 5 c b = 10 c Между ними находится 4 средних деления, а между каждыми средними делениями еще 4 мелких. Итого: 4+4·5=24 деления. |
Цена деления: \begin Физическую величину измеряют с помощью прибора Измерение длины бруска линейкой Физическую величину рассчитывают по формуле, куда подставляют значения величин, полученных с помощью прямых измерений Определение площади столешницы при измеренной длине и ширине Определяется погрешностью инструментов и приборов, используемых для измерений (принципом действия, точностью шкалы и т.п.) Определяется несовершенством методов и допущениями в методике. Погрешность теории (модели) Определяется теоретическими упрощениями, степенью соответствия теоретической модели и реальности. Определяется субъективным фактором, ошибками экспериментатора. Примеры значащих цифр: В простейших измерениях инструментальная погрешность прибора является основной. Пример получения результатов прямых измерений с помощью линейки: Второе измерение точнее, т.к. его относительная погрешность меньше. Измерение длины с помощью линейки (или объема с помощью мензурки) являются теми редкими случаями, когда для определения истинного значения достаточно одного измерения, а абсолютная погрешность сразу берется равной инструментальной погрешности, т.е. половине цены деления линейки (или мензурки). Гораздо чаще погрешность метода или погрешность оператора оказываются заметно больше инструментальной погрешности. В таких случаях значение измеренной физической величины каждый раз немного меняется, и для оценки истинного значения и абсолютной погрешности нужна серия измерений и вычисление средних значений. Пример расчета истинного значения и погрешности для серии прямых измерений: Составим расчетную таблицу: Сначала находим среднее значение всех измерений: \begin Как найти результат прямого измерения, мы рассмотрели выше. Вывод этих формул достаточно сложен, но если интересно, его можно найти в Главе 7 справочника по алгебре для 8 класса. Задача 1. Определите цену деления и объем налитой жидкости для каждой из мензурок. В каком случае измерение наиболее точно; наименее точно? Составим таблицу для расчета цены деления: Инструментальная точность мензурки равна половине цены деления. Наиболее точное измерение в 1-й мензурке, наименее точное – в 3-й мензурке. Ответ: Мерой точности является относительная погрешность измерений. Получаем: \begin Задача 3. Две машины движутся навстречу друг другу со скоростями 54 км/ч и 72 км/ч. Задача 4. Измеренная длина столешницы равна 90,2 см, ширина 60,1 см. Измерения проводились с помощью линейки с ценой деления 0,1 см. Найдите площадь столешницы, абсолютную и относительную погрешность этой величины. Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную. Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения: где а – приближенное значение числа х. Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа: Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность Рассмотрим различные причины возникновения погрешностей. Погрешность возникает из-за того, что сам численный метод или математическая модель является лишь приближением к точному методу (например, дифференцирование). Кроме того, любая математическая модель или метод могут внести существенные погрешности, если в ней не учтены какие-то особенности рассматриваемой задачи. Модель может прекрасно работать в одних условиях и быть совершенно неприемлемой в других. Такую погрешность называют также методической. Она всегда имеет место, даже при абсолютно точных данных и абсолютно точных вычислениях. В большинстве случаев погрешность численного метода можно уменьшить до требуемого значения за счет изменения параметров метода (например, уменьшением шага дискретизации, или увеличением количества итераций). Исходные данные задачи часто являются основным источником погрешностей. Ошибки такого типа неизбежны и проявляются в любых реальных задачах, поскольку любое измерение может быть проведено с только какой-то предельной точностью. Вместе с погрешностями, вносимыми математической моделью, их называют неустранимыми погрешностями, поскольку они не могут быть уменьшены ни до начала решения задачи, ни в процессе ее решения. Следует стремиться к тому, чтобы все исходные данные были примерно одинаковой точности. Сильное уточнение одних исходных данных при наличии больших погрешностей в других не приводит к повышению точности конечных результатов. Если какие-то отдельные точки данных (измерения) явно ошибочные, их можно исключить из вычислений. Ошибки этого типа проявляются из-за дискретной (а не непрерывной) формы представления величин в компьютере. Вычислительные ошибки можно свести к минимуму продуманно организовывая алгоритмы. Рассмотрим подробнее вычислительные ошибки. Допустим, исходные данные не имеют погрешности, но поскольку место в памяти компьютера, отведенное на хранение чисел, ограничено, и соответственно ограничена точность представления чисел, возникновение вычислительных ошибок неизбежно. Для хранения целых чисел (int, long, unsigned int и т.д.) обычно отводится 4 байта памяти, что позволяет представлять целые числа, находящиеся примерно в диапазоне от В вычислениях чаще используются вещественные числа (float, double). Такие числа представляются в компьютере в форме с плавающей точкой, и хранятся в логарифмическом виде – мантисса и порядок: где m – мантисса, p – порядок, а – основание степени. Например, число 273.9 можно В таблице А.1 приводится диапазон допустимых значений и другие параметры для чисел с плавающей точкой одинарной (float) и двойной (double) точности. Таблица A.1. Диапазон чисел, представимых в формате с плавающей точкой Для чисел с плавающей точкой существует понятие машинного эпсилон – наименьшего положительного число ε такого, что При вычислениях с помощью компьютера неизбежны погрешности округлений, связанные с ограниченностью хранимых разрядов мантиссы. Для приближенного числа, полученного в результате округления, абсолютная погрешность Перевод чисел из одной системы счисления в другую также может быть источником погрешности из-за того, что основание одной системы счисления не является степенью основания другой (например, 10 и 2). Это может привести к тому, что в новой системе счисления число невозможно представить абсолютно точно, например: При выполнении операций над приближенными числами можно оценить предельную погрешность результата в зависимости от выполняемой операции. При умножении или делении чисел друг на друга их относительные погрешности складываются: При возведении в степень приближенного числа его относительная погрешность умножается на показатель степени: При сложении или вычитании чисел их абсолютные погрешности складываются: Относительная погрешность суммы положительных слагаемых вычисляется как: Отсюда следует, что относительная погрешность суммы нескольких чисел одного и того же знака, заключена между наименьшей и наибольшей из относительных погрешностей слагаемых: На практике для оценки погрешности при сложении чисел обычно используют максимальную погрешность При сложении погрешность будет сильно завесить от абсолютных величин складываемых чисел. Рассмотрим пример сложения двух чисел с одинаковым количеством значащих цифр, но разных по абсолютному значению: 1234 + 0.005678 = 1234.00005678 или в компьютерном представлении: 1.234Е+03 + 5.678Е-03 = 1.234005678Е+03 После сложения количество значащих цифр равно 10. Число с одинарной точностью (float) позволяет хранить только 8 значащих цифр, то есть на самом деле число будет равно 1.2340056Е+03. Две значащие цифры потерялись в процессе сложения. Потеря точности здесь возникает из-за того, что при прибавлении к большому числу малых чисел результат сложения выходит за пределы точности при округлении. Для того чтобы уменьшить погрешность вычислений, нужно складывать числа в порядке возрастания их абсолютной величины. Таким образом можно минимизировать абсолютную величину промежуточной погрешности при каждом сложении. Рассмотрим теперь вычитание чисел (сложение чисел разного знака, или вычитание чисел одного знака). В соответствии с выражением (А.7) относительная погрешность может быть очень большой в случае, если числа близки между собой, так как даже при малых погрешностях Таким образом, можно сделать вывод, что сложение и вычисление являются плохо обусловленными (неустойчивыми) операторами, так как при некоторых данных даже небольшая погрешность в исходных данных может привести к большой погрешности результата. Уменьшить погрешность можно за счет правильной последовательности операций. Из-за погрешности округления в машинной арифметике важен порядок выполнения операций, и известные из алгебры законы коммутативности (и дистрибутивности) здесь не всегда выполняются. Основной качественной характеристикой любого датчика КИП является погрешность измерения контролируемого параметра. Погрешность измерения прибора это величина расхождения между тем, что показал (измерил) датчик КИП и тем, что есть на самом деле. Погрешность измерения для каждого конкретного типа датчика указывается в сопроводительной документации (паспорт, инструкция по эксплуатации, методика поверки), которая поставляется вместе с данным датчиком. По форме представления погрешности делятся на абсолютную, относительную и приведенную погрешности. Абсолютная погрешность – это разница между измеренной датчиком величиной Хизм и действительным значением Хд этой величины. Действительное значение Хд измеряемой величины это найденное экспериментально значение измеряемой величины максимально близкое к ее истинному значению. Говоря простым языком действительное значение Хд это значение, измеренное эталонным прибором, или сгенерированное калибратором или задатчиком высокого класса точности. Абсолютная погрешность выражается в тех же единицах измерения, что и измеряемая величина (например, в м3/ч, мА, МПа и т.п.). Так как измеренная величина может оказаться как больше, так и меньше ее действительного значения, то погрешность измерения может быть как со знаком плюс (показания прибора завышены), так и со знаком минус (прибор занижает). Относительная погрешность – это отношение абсолютной погрешности измерения Δ к действительному значению Хд измеряемой величины. Относительная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения. Приведенная погрешность – это отношение абсолютной погрешности измерения Δ к нормирующему значению Хn, постоянному во всем диапазоне измерения или его части. Нормирующее значение Хn зависит от типа шкалы датчика КИП: Приведенная погрешность выражается в процентах, либо является безразмерной величиной, а также может принимать как положительные, так и отрицательные значения. Довольно часто в описании на тот или иной датчик указывается не только диапазон измерения, например, от 0 до 50 мг/м3, но и диапазон показаний, например, от 0 до 100 мг/м3. Приведенная погрешность в этом случае нормируется к концу диапазона измерения, то есть к 50 мг/м3, а в диапазоне показаний от 50 до 100 мг/м3 погрешность измерения датчика не определена вовсе – фактически датчик может показать все что угодно и иметь любую погрешность измерения. Диапазон измерения датчика может быть разбит на несколько измерительных поддиапазонов, для каждого из которых может быть определена своя погрешность как по величине, так и по форме представления. При этом при поверке таких датчиков для каждого поддиапазона могут применяться свои образцовые средства измерения, перечень которых указан в методике поверки на данный прибор. У некоторых приборов в паспортах вместо погрешности измерения указывают класс точности. К таким приборам относятся механические манометры, показывающие биметаллические термометры, термостаты, указатели расхода, стрелочные амперметры и вольтметры для щитового монтажа и т.п. Класс точности – это обобщенная характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений. При этом класс точности не является непосредственной характеристикой точности измерений, выполняемых этим прибором, он лишь указывает на возможную инструментальную составляющую погрешности измерения. Класс точности прибора наноситься на его шкалу или корпус по ГОСТ 8.401-80. Определение погрешности измерения датчиков выполняют, например, при их периодической поверке и калибровке. С помощью различных задатчиков и калибраторов с высокой точностью генерируют определенные значения той или иной физической величины и сличают показания поверяемого датчика с показаниями образцового средства измерения, на которое подается то же самое значение физической величины. Причем погрешность измерения датчика контролируется как при прямом ходе (увеличение измеряемой физической величины от минимума до максимума шкалы), так и при обратном ходе (уменьшение измеряемой величины от максимума до минимума шкалы). Это связано с тем, что из-за упругих свойств чувствительного элемента датчика (мембрана датчика давления), различной интенсивности протекания химических реакций (электрохимический сенсор), тепловой инерции и т.п. показания датчика будут различны в зависимости от того, как меняется воздействующая на датчик физическая величина: уменьшается или увеличивается. Довольно часто в соответствии с методикой поверки отсчет показаний датчика при поверке нужно выполнять не по его дисплею или шкале, а по величине выходного сигнала, например, по величине выходного тока токового выхода 4…20 мА. У поверяемого датчика давления со шкалой измерения от 0 до 250 mbar основная относительная погрешность измерения во всем диапазоне измерений равна 5%. Датчик имеет токовый выход 4…20 мА. На датчик калибратором подано давление 125 mbar, при этом его выходной сигнал равен 12,62 мА. Необходимо определить укладываются ли показания датчика в допустимые пределы. Во-первых, необходимо вычислить каким должен быть выходной ток датчика Iвых.т при давлении Рт = 125 mbar. Iвых.т = Iш.вых.мин + ((Iш.вых.макс – Iш.вых.мин)/(Рш.макс – Рш.мин))*Рт где Iвых.т – выходной ток датчика при заданном давлении 125 mbar, мА. Iш.вых.мин – минимальный выходной ток датчика, мА. Для датчика с выходом 4…20 мА Iш.вых.мин = 4 мА, для датчика с выходом 0…5 или 0…20 мА Iш.вых.мин = 0. Рш.макс – максимум шкалы датчика давления, mbar. Рш.макс = 250 mbar. Рш.мин – минимум шкалы датчика давления, mbar. Рш.мин = 0 mbar. Рт – поданное с калибратора на датчик давление, mbar. Рт = 125 mbar. Подставив известные значения получим: То есть при поданном на датчик давлении равном 125 mbar на его токовом выходе должно быть 12 мА. Считаем, в каких пределах может изменяться расчетное значение выходного тока, учитывая, что основная относительная погрешность измерения равна ± 5%. То есть при поданном на датчик давлении равном 125 mbar на его токовом выходе выходной сигнал должен быть в пределах от 11,40 до 12,60 мА. По условию задачи мы имеем выходной сигнал 12,62 мА, значит наш датчик не уложился в определенную производителем погрешность измерения и требует настройки. Основная относительная погрешность измерения нашего датчика равна: Поверка и калибровка приборов КИП должна выполнятся при нормальных условиях окружающей среды по атмосферному давлению, влажности и температуре и при номинальном напряжении питания датчика, так как более высокие или низкие температура и напряжение питания могут привезти к появлению дополнительной погрешности измерения. Условия проведения поверки указываются в методике поверки. Приборы, погрешность измерения которых не уложилась в установленные методикой поверки рамки либо заново регулируют и настраивают, после чего они повторно проходят поверку, либо, если настройка не принесла результатов, например, из-за старения или чрезмерной деформации сенсора, ремонтируются. Если ремонт невозможен то приборы бракуются и выводятся из эксплуатации. Если все же приборы удалось отремонтировать то они подвергаются уже не периодической, а первичной поверке с выполнением всех изложенных в методике поверки пунктов для данного вида поверки. В некоторых случаях прибор специально подвергают незначительному ремонту (с отметкой в паспорте) так как по методике поверки выполнить первичную поверку оказывается существенно легче и дешевле чем периодическую, из-за различий в наборе образцовых средств измерения, которые используются при периодической и первичной поверках. Для закрепления и проверки полученных знаний рекомендую выполнить тестовое задание.п.3. Виды измерений
п.4. Погрешность измерений, абсолютная и относительная погрешность
0,403 – три значащих цифры, величина определена с точностью до тысячных.
40,3 – три значащих цифры, величина определена с точностью до десятых.
40,300 – пять значащих цифр, величина определена с точностью до тысячных.
В таких случаях физическую величину измеряют один раз, полученное значение берут в качестве истинного, а абсолютную погрешность считают равной инструментальной погрешности прибора.
Примеры измерений с абсолютной погрешностью равной инструментальной:п.5. Абсолютная погрешность серии измерений
Пусть при измерении массы шарика с помощью рычажных весов мы получили в трех опытах следующие значения: 99,8 г; 101,2 г; 100,3 г.
Инструментальная погрешность весов d = 0,05 г.
Найдем истинное значение массы и абсолютную погрешность.№ опыта 1 2 3 Сумма Масса, г 99,8 101,2 100,3 301,3 Абсолютное отклонение, г 0,6 0,8 0,1 1,5
Затем считаем абсолютное отклонение каждого опыта как модуль разности \(m_0\) и измерения. \begin
Поэтому абсолютная погрешность измерения массы: \begin п.6. Представление результатов эксперимента
Результат косвенного измерения зависит от действий, которые производятся при подстановке в формулу величин, полученных с помощью прямых измерений.п.7. Задачи
№ мензурки a, мл b, мл n \(\triangle=\frac 1 20 40 4 \(\frac<40-20><4+1>=4\) 2 100 200 4 \(\frac<200-100><4+1>=20\) 3 15 30 4 \(\frac<30-15><4+1>=3\) 4 200 400 4 \(\frac<400-200><4+1>=40\)
Принимаем инструментальную точность за абсолютную погрешность и измеренное значение объема за истинное.
Составим таблицу для расчета относительной погрешности (оставляем две значащих цифры и округляем с избытком):№ мензурки Объем \(V_0\), мл Абсолютная погрешность
\(\triangle V=\frac<\triangle><2>\), млОтносительная погрешность
\(\delta_V=\frac<\triangle V>1 68 2 3,0% 2 280 10 3,6% 3 27 1,5 5,6% 4 480 20 4,2%
Цена деления 4; 20; 3; 40 мл
Объем 68; 280; 27; 480 мл
Самое точное – 1-я мензурка; самое неточное – 3-я мензурка
Ответ: \(\delta_2\lt \delta_1\), второе измерение точней.
Цена деления спидометра первой машины 10 км/ч, второй машины – 1 км/ч.
Найдите скорость их сближения, абсолютную и относительную погрешность этой величины.Приложение А. Погрешности вычислений
Абсолютная и относительная погрешности
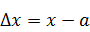
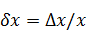


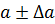
Источники погрешностей
Математическая модель задачи является неточной
Ошибки в исходных данных
Вычислительные ошибки (ошибки округления)
Вычислительные ошибки
Представление чисел с плавающей точкой
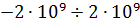
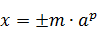
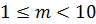
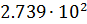
Точность Одинарная Двойная Размер (байты) 4 8 Наименьшее значение 1.2·10 −38 2.3·10 −308 Наибольшее значение 3.4×10 +38 1.7×10 +308 Размеры степени и мантиссы (биты) 8-23 11-52 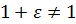
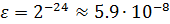
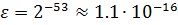
Погрешность округления

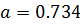
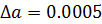
Погрешность арифметических действий над приближенными числами
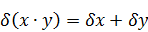
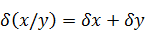
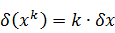
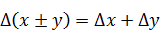
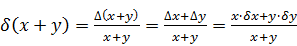
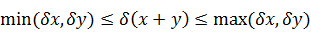
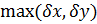
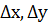
Погрешности измерения датчиков КИП. Классы точности
ООП основная относительная погрешность ОПП основная приведенная погрешность ОАП основная абсолютная погрешность