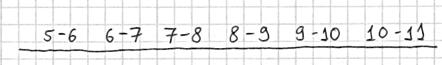Что показывают частоты в вариационном ряду

3. Интервальный вариационный ряд.
Гистограмма относительных частот

На предыдущем уроке по математической статистике (Занятие 1) мы разобрали дискретный вариационный ряд (Занятие 2), и сейчас на очереди интервальный. Его понятие, графическое представление (гистограмма и эмпирическая функция распределения), а также рациональные методы вычислений, как ручные, так и программные. В том числе будут рассмотрены задачи с достаточно большим количеством (100-200) вариант – что делать в таких случаях, как обработать большой массив данных.

Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений. Зачастую ИВР появляется в результате измерения непрерывной характеристики изучаемых объектов. Типично – это время, масса, размеры и другие физические характеристики. Подходящие примеры встретились в первой же статье по матстату, вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.

Для изучения интервального вариационного ряда затруднительно либо невозможно применить тот же подход, что и для дискретного ряда. Это связано с тем, что ВСЕ варианты многих ИВР различны. И даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, ибо полученные значения всё равно отличаются хоть какими-то микрограммами.

Поэтому для исследования ИВР используется другой подход, а именно, определяется интервал, в пределах которого варьируются значения, затем данный интервал делится на частичные интервалы, и по каждому интервалу подсчитываются частоты – количество вариант, которые в него попали.

Разберём всю кухню на конкретной задаче, и чтобы как-то разнообразить физику, я приведу пример с экономическим содержанием, кои десятками предлагают студентам экономических отделений. Деньги, строго говоря, дискретны, но если надо, непрерывны :), и по причине слишком большого разброса цен, для них целесообразно строить интервальный ряд:

По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в некоторых денежных единицах):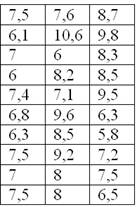

Требуется составить вариационный ряд распределения, построить гистограмму и полигон относительных частот + бонус – эмпирическую функцию распределения.

Такое обывательское исследование проводит каждый из нас, начиная с анализа цены на пакет молока вот это дожил в нескольких магазинах, и заканчивая ценами на недвижимость по гораздо бОльшей выборке. Что называется, не какие-то там унылые сантиметры.

Поэтому представьте свой любимый товар / услугу и наслаждайтесь решением🙂

Очевидно, что перед нами выборочная совокупность объемом 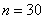наблюдений (таблица 10*3), и вопрос номер один: какой ряд составлять – дискретный или интервальный? Смотрим на таблицу: среди предложенных цен есть одинаковые, но их разброс довольно велик, и поэтому здесь целесообразно провести интервальное разбиение. К тому же цены могут быть округлёнными.

Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только ручка, карандаш, тетрадь и калькулятор.

Тактика действий похожа на исследование дискретного вариационного ряда. Сначала окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае напрашиваются промежутки единичной длины. Записываем их на черновик:

Теперь начинаем вычёркивать числа из исходного списка и записывать их в соответствующие колонки нашей импровизированной таблицы: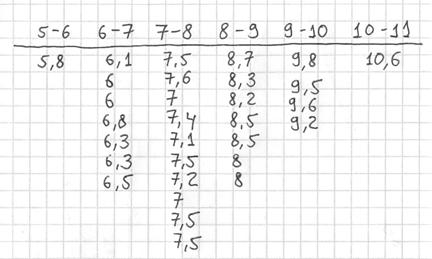

После этого находим самое маленькое число в левой колонке и самое большое значение – в правой. Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – хорошим тоном считается указывать размерность.

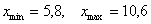
Вычислим размах вариации:
ден. ед. – длина общего интервала, в пределах которого варьируется цена.

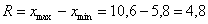
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт существует формула Стерджеса:

, где – десятичный логарифм* от объёма выборки и – оптимальное количество интервалов, при этом результат округляют до ближайшего левого целого значения.

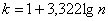
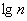
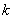
* есть на любом более или менее приличном калькуляторе

В нашем случае получаем:
интервалов.

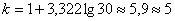
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии задачи прямо сказано, на какое количество интервалов нужно проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует придерживаться именно этого указания.

Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную группировку:
– длина частичного интервала. В принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.

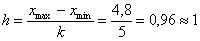
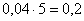
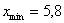
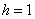
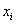
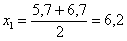
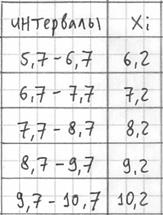
И коль скоро мы прибавили 0,04, то по 5 частичным интервалам у нас получается «перебор»: . Посему от самой малой варианты отмеряем влево 0,1 влево (половину «перебора») и к значению 5,7 начинаем прибавлять по , получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например, ) – они требуются почти во всех тематических задачах:

– убеждаемся в том, что самая большая варианта 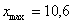вписалась в последний частичный интервал и отстоит от его правого конца на 0,1.

Далее подсчитываем частоты по каждому интервалу. Для этого в черновой «таблице» обводим значения, попавшие в тот или иной интервал, подсчитываем их количество и вычёркиваем: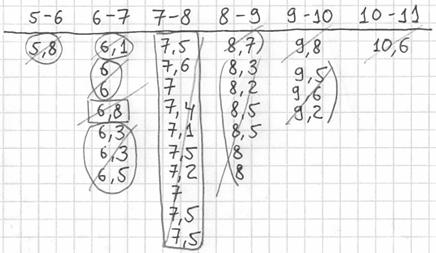

Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11 штук) и вычеркнул и так далее.

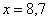
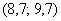
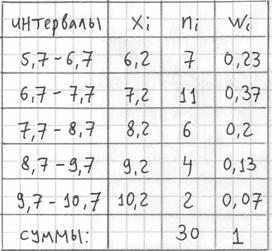
Правило: если варианта попадает на «стык» интервалов, то её следует относить в правый интервал. У нас такая варианта встретилась одна: – и её нужно причислить к интервалу .

В результате получаем интервальный вариационный ряд, при этом обязательно убеждаемся в том, что ничего не потеряно: , и, кроме того, рассчитываем относительные частоты по каждому интервалу, которые уместно округлить до двух знаков после запятой:

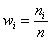
Дело за чертежами. Для ИВР чаще всего требуется построить гистограмму.

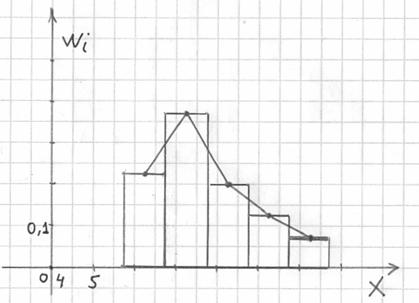
Гистограмма относительных частот – это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота – соответствующим относительным частотам: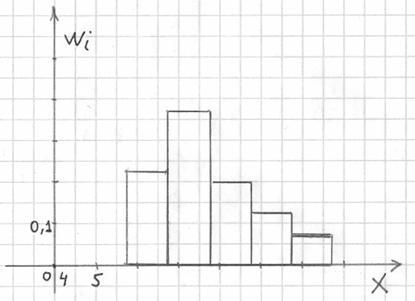

При этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх.

Площадь гистограммы равна единице, и это статистический аналог функции плотности распределения непрерывной случайной величины. Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной совокупности. Но это при условии, что выборка представительна.

Вместе с гистограммой нередко требуют построить полигон. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки , где – середины интервалов:

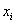
Автоматизируем решение в Экселе:

Как составить ИВР и представить его графически? (Ютуб)

И бонус – эмпирическая функция распределения. Она определяется точно так же, как в дискретном случае:

, где – количество вариант СТРОГО МЕНЬШИХ, чем «икс», который «пробегает» все значения от «минус» до «плюс» бесконечности.

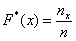
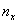
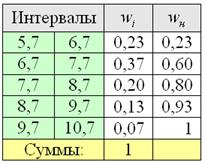
Но вот построить её для интервального ряда намного проще. Находим накопленные относительные частоты:

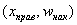
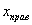
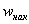
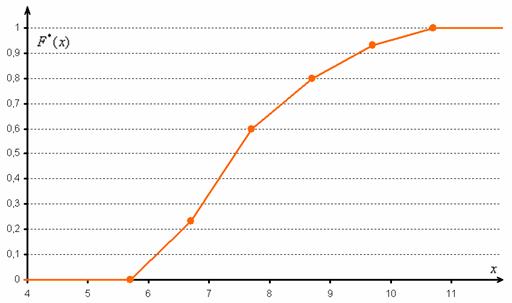
И строим кусочно-ломаную линию, с промежуточными точками , где – правые концы интервалов, а – относительная частота, которая успела накопиться на всех «пройденных» интервалах:

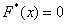
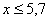
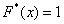
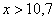
При этом если и если .

Напоминаю, что данная функция не убывает, принимает значения из промежутка 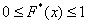и, кроме того, для ИВР она ещё и непрерывна.

Эмпирическая функция распределения является аналогом функции распределения НСВ и приближает теоретическую функцию 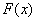, которую теоретически, а иногда и практически можно построить по всей генеральной совокупности.

Помимо перечисленных графиков, вариационные ряды также можно представить с помощью кумуляты и огивы частот либо относительных частот, но в классическом учебном курсе эта дичь редкая, и поэтому о ней буквально пару абзацев:

Кумулята – это ломаная, соединяющая точки:

* либо – для дискретного вариационного ряда;
либо – для интервального вариационного ряда.

* – накопленные «обычные» частоты

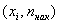
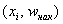
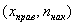
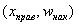
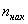
В последнем случае кумулята относительных частот 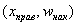представляет собой «главный кусок» недавно построенной эмпирической функции распределения.

Огива – это обратная функция по отношению к кумуляте – здесь варианты откладываются по оси ординат, а накопленные частоты либо относительные частоты – по оси абсцисс.

С построением данных линий, думаю, проблем быть не должно, чего не скажешь о другой проблеме. Хорошо, если в вашей задаче всего лишь 20-30-50 вариант, но что делать, если их 100-200 и больше? В моей практике встречались десятки таких задач, и ручной подсчёт здесь уже не торт. Считаю нужным снять небольшое видео:

Как быстро составить ИВР при большом объёме выборки? (Ютуб)

Ну, теперь вы монстры 8-го уровня 🙂

Но не всё так сурово. В большинстве задач вам предложат готовый вариационный ряд, и на счёт молока, то, конечно, была шутка:

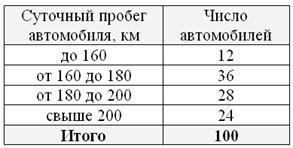
Выборочная проверка партии чая, поступившего в торговую сеть, дала следующие результаты:

Требуется построить гистограмму и полигон относительных частот, эмпирическую функцию распределения

Проверяем свои навыки работы в Экселе! (исходные числа и краткая инструкция прилагается) И на всякий случай краткое решение для сверки в конце урока.

Что ещё важного по теме? Время от времени встречаются ИВР с открытыми крайними интервалами, например:

В таких случаях, что убийственно логично, интервалы «закрывают». Обычно поступают так: сначала смотрим на средние интервалы и выясняем длину частичного интервала: 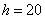км. И для дальнейшего решения можно считать, что крайние интервалы имеют такую же длину: от 140 до 160 и от 200 до 220 км. Тоже логично. Но уже не убийственно:)

Ну вот, пожалуй, и вся практически важная информация по ИВР.

На очереди числовые характеристики вариационных рядов и начнём мы с их центральных характеристик, а именно – Моды, медианы и средней.

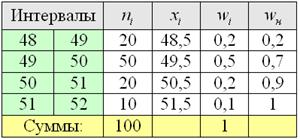
Пример 7. Решение: заполним расчётную таблицу

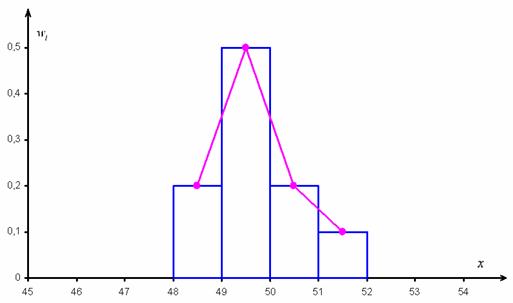
Построим гистограмму и полигон относительных частот:

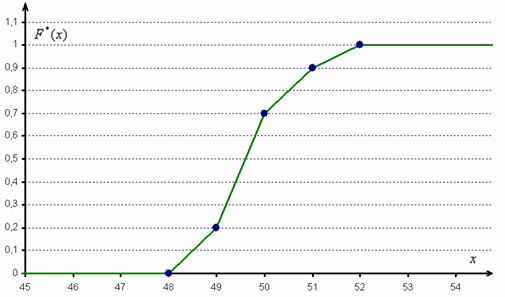
Построим эмпирическую функцию распределения:

Автор: Емелин Александр

(Переход на главную страницу)

Zaochnik.com – профессиональная помощь студентам

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5

Tutoronline.ru – онлайн репетиторы по математике и другим предметам

Источник

Вариация. Виды вариационных рядов. Показатели вариации.

Причины вариации могут быть самыми разными.

Вариация присуща практически всем явлениям природы и общества, за исключением неких закрепленных нормативных значений неких социальных признаков.

Измерение вариации, причин, факторов очень важно, так как это дает базу для принятия управленческих решений.

1) Размах вариации. Абсолютная величина разности между максимальными и минимальными значениями некого признака. Зависит от колебания крайних величин.

2) Среднее линейное отклонение. Характеризует среднюю арифметическую абсолютного значения.

3) Среднее квадратичное отклонение.

Вариационный ряд – упорядоченное распределение единиц совокупности (чаще по возрастающей или реже по убывающей) значения признака, и подсчет числа единиц с тем или иным значением признака.

1) Ранжированный ряд – перечень отдельных единиц совокупности в порядке возрастания или убывания изучаемого признака.

2) Дискретный вариационный ряд. Формируется в виде таблицы, которая состоит из двух строк, в которых будут конкретные значения варьирующего признака, а во второй строке будет число единиц совокупности в данной строке признака.

3) Интервальный ряд. Интервальный вариационный ряд строится и для изучения признаков, которые могут принимать любые, как целые, так и дробные значения в области своего существования. Таковы, например, рентабельность реализованной продукции

Показатели вариации:

1) Показатели центра распределения и структурные характеристики вариационного ряда:

· Средняя величина признака: по формуле средней арифметической взвешенной

2) Показатели размера и интенсивности вариации

· Размах вариации: разность между максимальным и минимальным значениями признака в совокупности.

· Среднее линейное отклонение

· Среднее квадратическое отклонение (его квадрат – это дисперсия)

· Коэффициент вариации: среднее квадратическое отклонение/среднюю арифметическую величину

Абсолютные показатели вариации включают:

· Размах вариации — это разность между максимальным и минимальным значениями признака

· Среднее линейное отклонение — это средняя арифметическая из абсолютных отклонений отдельных значений признака от средней.

· Дисперсия — представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины.

· Среднее квадратическое отклонение ( ) равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Относительные показатели вариации включают:

Ряды распределения.

Статистические ряды распределения –систематизируемая последовательность статистических единиц, сгруппированных по определенному признаку.

Ряд распределения состоит из 2 элементов: вариантов – значений признака и частот. Именно при соотношении их и проявляется закономерность распределения.

Атрибутивный – это ряд распределения, построенный по качественным признакам(по описательному признаку,т.е не имеющих числового выражения).

Пр: по полу, виду занятости, предприятие – сфера деятельности/ форма собственности

Вариационный – это ряд распределения, построенный по количественному признаку.

Пр: население по возрасту, работник-год стажа, з.п, объем выработки.

Вариационные ряды:

4) Дискретный— основаны на дискретных/прерывных признаках, имеющих только целые значения (пр: число детей в семье).

· равноинтервальные – постоянная ширина интервала

· неравноинтервальные – ширина интервала различна для разных групп

Построение вар ряда – упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака и подсчет числа единиц с тем или иным значением.

3 главных элемента:

1. варианты – значения исследуемого признака

· если ряд дискретный, то значение признака – число

· если интервальный, то выбираем интервал, куда попадает значение признака

2. частоты – число единиц совокупности, обладающих данным значением признака, т.е сколько раз значение признака встречается в данной совокупности)

3. частость – удельный вес или доля единиц совокупности, имеющих определенное значение признака.

Полученный вариационный ряд оформляют в виде таблицы, где в первой графе указывают варианты(интервалы) значений признака, в следующих – частоту.

Способы построения вариационного ряда для дискретных и непрерывных признаков различны:

Если дискретная вариация проявляется в широких пределах, то, как и при непрерывной вариации, строятся интервальные вариац. ряды. При группировке единиц однокачественной совокупности можно использовать равные интервалы.

Если вар ряд представлен неравными интервалами, то частоты в отдельных интервалах непосредственно несопоставимы, т.к. они зависят от ширины интервала. Для сравнения частот в разных интервалах рассчитывают показатели абсолютной и относительной плотности распределения.

· абсолютная – показывает число единиц совокупности, приходящихся на единицу ширины интервала в значениях признака(соотношение частоты к величине интервала).

· относительная – показывает удельный вес единиц сов-ти, приход на единицу ширины интервала(соотношение частности к величине интервала).

Для описания распределения совокупности могут использоваться и кумулятивные ряды(-ряд значений числа единиц совокупности с меньшим или равным верхней границе соответствующими интервала значениями признака), т.е. ряды накопленных частот. Накопленная частота – число единиц совокупности, у которых значение признака не превышает некоего данного значения(считается нарастающим итогом)

+? Графическое изображение ВР(для ознакомления):

При построении полигона на горизонтальной оси (ось абсцисс) откладывают значения варьирующего признака, а на вертикальной оси (ось ординат) — частоты или частости.

Гистограмма

Для построения гистограммы по оси абсцисс указывают значения границ интервалов и на их основании строят прямоугольники, высота которых пропорциональна частотам (или частостям).

Кумулята

Распределение признака в вариационном ряду по накопленным частотам (частостям) изображается с помощью кумуляты.

Кумулята или кумулятивная кривая в отличие от полигона строится по накопленным частотам или частостям. При этом на оси абсцисс помещают значения признака, а на оси ординат — накопленные частоты или частости

Правила построения вариационных рядов:

Правила построения рядов распределения аналогичны правилам построения группировки.

Группировки, построенные за один и тот же период времени, но для разных объектов или, наоборот, для одного объекта, но за два разных периода времени могут оказаться несопоставимыми из-за различного числа выделенных групп или неодинаковости границ интервалов.

При построении интервального ряда большое значение имеет также принцип его

Существуют следующие принципы построения интервальных рядов:

1. Арифметический (равенства интервалов);

Выбор того или иного принципа зависит от степени однородности совокупности.

1. Если совокупность вполне однородна по составу и последний член ранжированного ряда в небольшое число раз превышает начальный ñ применяют принцип равенства интервалов (арифметический). Т.е. образуют группы с равными интервалами, в которых ряд нижних границ, например, образует арифметическую прогрессию. В качестве примера можно привести распределение рабочих по затратам времени

2. Если же значения изучаемого признака варьируют в больших пределах, то целесообразно применить принцип кратных интервалов (геометрический). В этом случае (в этой шкале) интервалы не равны друг другу, а непрерывно увеличиваются по законам геометрической прогрессии.

3. В случае, если статистическая совокупность разнородна по составу, в основу построения интервального ряда закладывается экономический критерий. Он позволяет сгруппировать совокупность в группы, однородные в социально-экономическом отношении по типам. Поэтому этот принцип и называется типологическим. В качестве примера можно взять распределение городов региона по количеству жителей

Источник