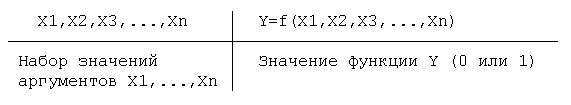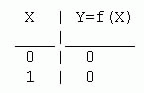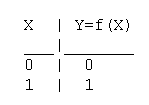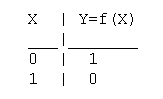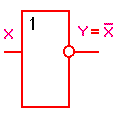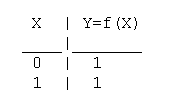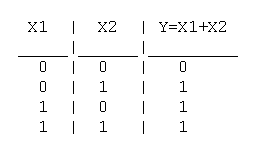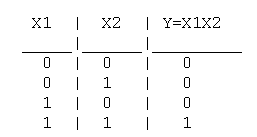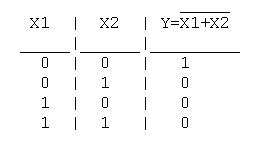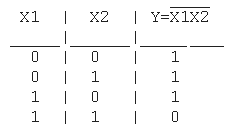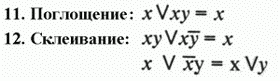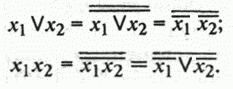Что понимается под логической функцией какие значение может принимать логическая функция
Логическая функция: что такое, способы представления, значение
Содержание:
Логическая функция — это такая функция, которая может принимать только одно из 2-х значений: 0 («ложь», «false») или 1 («истина», «true»). Логическую функцию можно обозначить как F (A), где А — это логический аргумент, чье количество в функции никак не ограничено.
Любая современная компьютерная система состоит из множества логических схем, где присутствуют логические функции и логические переменные. Для того чтобы описать эти взаимоотношения, есть таблицы истинности, в которых расписаны значения логической функции для разных наборов аргументов функции.
Логическая функция, что это
Логическая функция: отрицание
Логическая функция: конъюнкция
Логическая функция: дизъюнкция
Эта логическая функция, как и предыдущая, должна быть представлена несколькими аргументами. Ее значение буде «false» только в том случае, когда значения всех аргументов будет «false», во всех остальных случаях она будет «true».
Например нам даны два аргумента «А и В», тогда их таблица дизъюнкции будет выглядеть следующим образом:
Логическая функция: импликация
Логическая функция «импликация» — это такое выражение, которое показывает зависимость одного аргумента от другого. Его еще можно «прочитать» как «если А, то В». Обозначается как «А→В» и оно будет считаться «false» только тогда, когда А будет «true», а «В» будет «false».
Логическая функция: эквиваленция
Логическая функция «эквиваленция» простыми словами может читаться как «для А нужно и достаточно В». Его значение будет «true», только тогда, когда А и В вместе, либо «false», либо «true». Такая функция обозначается как «А↔В».
Вот как выглядит таблица истинности эквиваленции:
Что понимается под логической функцией какие значение может принимать логическая функция
Логические элементы и логические функции.
Элементы математической логики.
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.
таблицей, которая называется таблицей истинности.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
Таблица истинности функции повторения имеет вид:
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Таблица истинности логического ИЛИ имеет вид:
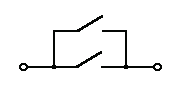
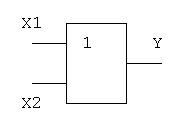
Логический элемент ИЛИ обозначается на схемах следующим образом:
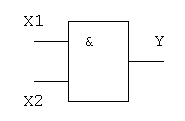
2. Логическое И (логическое умножение, конъюнкция, схема совпаде-
Таблица истинности логического И имеет вид:
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
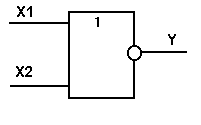
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом :
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)
Таблица истинности функции И-НЕ имеет вид:
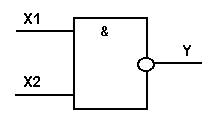
Логический элемент И-НЕ обозначается на схемах следующим образом:
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2). Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
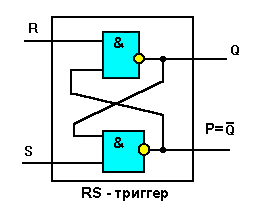
формации. К триггерам относятся устойства, имеющие два устойчивых
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
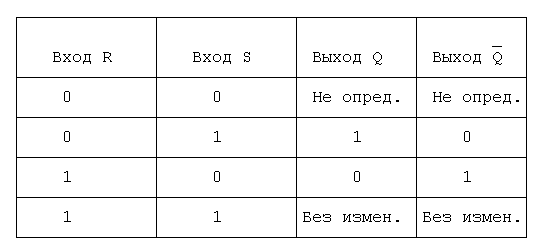
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
В обычном (исходном) состоянии на входы триггера поданы 1. Для
записи информации на вход R подан 0. Для сброса информации и под-
готовки к приёму новой информации на вход S подается 0 и триггер
вернётся в исходное состояние.
Поскольку один триггер запоминает 1 бит информации, то для запо-
минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб
(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо-
собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
формальные математические методы.
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):
Кроме того, применяются ещё три соотношения:
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи
на свойства умножения, поэтому её часто называют логическим умно-
жением. Из законов 6 и 8 следует, что используя отрицание, дизъ-
юнкцию можно выразить через конъюнкцию, и наоборот:
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио-
нально полными или базисными.
1. Что такое логическая функция и логический элемент?
2. Что такое таблица истинности и сколько в ней строк?
3. Какие функции одной переменной Вы знаете? Какая из них являет-
4. Как зависит число функций от числа переменных?
5. Что такое конъюнкция и дизъюнкция? Как они реализуются?
6. Что такое функция стрелка Пирса? Какова её таблица истинности?
7. Что такое функция штрих Шеффера? Какова её таблица истинности?
8. Что такое базисная функция и какие базисы Вы знаете?
9. Что такое логика? Какие два подхода существуют в логике?
10. Как доказывается истинность или ложность высказываний? Приве-
дите примеры из практики.
11. Что такое булева алгебра?
12. Какие законы булевой алгебры Вы знаете? Где они применяются?
13. Что такое триггер? Как работает RS-триггер?
14. Сколько надо триггеров, чтобы запомнить 1 Мб информации?
Логические функции, способы их задания
Определение. Функция f(x0, x1, …, xn) называется логической (булевой), если ее аргументы x0, x1, …, xn и значения функции могут принимать только два значения: логического 0 и логической 1.
Способы задания логических функций
1. Словесный. Взаимосвязь значений функции и ее аргументов описывается словесной формулировкой.
2. Табличный. При табличном способе строится таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов. В отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов.
3. Цифровой. Функцию алгебры логики определяют в виде последовательности десятичных чисел. При этом последовательно расписывают эквиваленты двоичных кодов, которые соответствуют единичным либо нулевым значениям функции.
4. Аналитический. Функция алгебры логики записывается в виде аналитического выражения, где показаны логические операции, выполняемые над аргументами функции.
Логические функции одной переменной
Существует 4 функции одной переменной.
Таблица истинности для функций одной переменной
| Аргумент х | Функции | ||
| f0 | f1 | f2 | f3 |
Функции одного аргумента имеют следующие аналитические записи и названия:
f2(х) =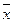 
отрицание х, НЕ, инверсия, читается «не х»;
f3(х) = 1 — константа единицы.
Функции одной переменной f0, f1, f3 не представляют интереса с точки зрения технической реализации. Практически применяется только функция
f2(х) = 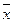— инверсия.
Логические функции двух переменных
Существует 16 функций двух переменных (табл. 3.3).
Таблица истинности для функций двух переменных
| Аргументы | Функции | ||||||||||||||||
| х1 | х2 | f0 | f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 | f10 | f11 | f12 | f13 | f14 | f15 |
Функции двух переменных имеют следующие записи и названия:
f8(х1, x2) =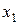 
Úх2=х1¯х2 — стрелка Пирса, отрицание ИЛИ; ИЛИ-НЕ;
f10(х1, x2)=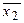 
—отрицание х2;
f12(х1, x2) =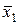 
— отрицание х1;
f14(х1, x2) = х1½х2 =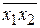 
— штрих Шеффера, отрицание И; И-НЕ;
Из функций двух переменных не имеют практического интереса f0 (константа 0), f3 (повторение x1), f5 (повторение х2), f15 (константа 1).
Приведем словесное описание некоторых функций.
Логическое сложение (дизъюнкция). Функция ИЛИ принимает единичное значение, когда хотя бы один из аргументов ИЛИ х1, ИЛИ х2 равен единице.
Логическое умножение (конъюнкция). Функция И принимает единичное значение, когда одновременно обе переменные И x1, И х2 равны единице.
Инверсия. Функция НЕ принимает значения, противоположные аргументу х.
Цифровую форму представления логической функции рассмотрим на примере функции f6, которая принимает единичные значения на наборах входных переменных (х1х2) в двоичном коде 01, 10, что соответствует десятичному эквиваленту 1; 2:
Функция f6 принимает нулевые значения на наборах входных переменных (х1х2) в двоичном коде 00,11. Это соответствует в десятичном коде 0; 3:
Логические функции одной и двух переменных называются элементарными. Они предполагают проведение только одной логической операции.
Логические функции и способы их записи
В устройствах цифровой электроники используются элементы, входные и выходные сигналы которых могут принимать только два значения, соответствующие логической 1 («1») и логическому 0 («0»). Такие элементы называют логическими. С их помощью реализуют простейшие операции с двоичными числами (то есть с числами двоичной системы счисления).
Для описания алгоритмов работы и структуры цифровых схем используют аппарат алгебры логики (или булевой алгебры – по имени разработавшего ее в середине XIX века ирландского математика Д. Буля). В ее основе лежат три логические операции над логическими переменными:
— логическое отрицание (операция НЕ, инверсия), обозначаемое надчеркиванием над логической переменной или логическим выражением, например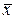 
, 
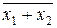
и т. д.;
— логическое сложение (операция ИЛИ, дизъюнкция), обозначаемое знаком «+» или «Ú»;
— логическое умножение (операция И, конъюнкция), обозначаемое одним из знаков: «´», «×», «&», «Ù» или отсутствием какого-либо знака между переменными, например х1х2.
Логическими переменными (булевыми переменными) называются переменные х1, х2, …, хп, которые могут принимать только два значения – 0 и 1, то есть хi Î <0, 1>.
Совокупность п логических переменных называется набором переменных и обозначается х1, х2, …, хп. В общем случае может быть 2 п наборов логических переменных.
Каждая логическая операция задает соответствующую логическую функцию своих переменных. Следовательно, можно говорить о трех логических функциях: конъюнкции(y=х1×х2×…×хп), дизъюнкции(y=х1+x2+…+хп), инверсии (y= 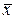). Число аргументов (переменных) функций дизъюнкции и конъюнкции в общем случае может быть произвольным (больше двух).
Система логических функций называется функционально полной, если при помощи функций, входящих в систему, можно выразить любую сколь угодно сложную булеву функцию.
В математической логике доказывается, что если система булевых функций содержит функции конъюнкцию, дизъюнкцию и инверсию, то она является функционально полной.
Функциональной полнотой обладают и некоторые другие системы, например, система, состоящая из одной логической функции И – НЕ («штрих Шеффера»,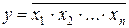 
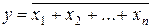
) и система, содержащая единственную логическую функцию ИЛИ – НЕ («стрелка Пирса», 
).
Логическую функцию можно описать несколькими способами:
-с помощью алгебраического выражения (в аналитическом виде);
-с помощью последовательности десятичных чисел и др.
Рисунок 5.4 – Таблица истинности логической функции у = f(х1, х2)
В первом столбце таблицы истинности записаны номера наборов логических переменных, численно равные десятичному эквиваленту двоичного числа xпxп-1 … x2x1, составленного из значений логических переменных (второй и третий столбцы). В последнем столбце записаны значения логической функции на соответствующих наборах логических переменных.
В общем случае логическая функция может быть определена не на всех наборах логических переменных (то есть может быть недоопределенной). Некоторых сочетаний значений логических переменных на входе цифрового устройства, описываемого логической функцией, может просто не существовать. В этом случае набор переменных называется запрещенным, а в таблице истинности напротив запрещенного набора вместо значения функции обычно записывают знак «*» (рисунок 5.5). В приведенном примере запрещенными являются наборы логических переменных с номерами 2, 5 и 6.
Логические функции от одной и двух переменных принято называть элементарными. Эти функции имеют специальные названия и обозначения и используются при воспроизведении более сложных логических функций. В таблице 5.1 приведены все возможные логические функции двух переменных.
Для аналитической записи логических функций используются вспомогательные функции, называемые конституентой единицы и конституентой нуля.
| №№ наборов | х3 | х2 | х1 | у |
| * | ||||
| * | ||||
| * |
Рисунок 5.5 – Пример таблицы истинности недоопределенной
| fi | х2 | Название функции | Вид функции |
| х1 | |||
| f0 | Константа 0 | f0(x1, x2) = 0 | |
| f1 | Конъюнкция | f0(x1, x2) = x1×x2 | |
| f2 | Функция запрета по x2 | f0(x1, x2) =  | |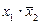
| f3 | Переменная x1 | f0(x1, x2) = x1 | |
| f4 | Функция запрета по x1 | f0(x1, x2) =  | |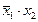
| f5 | Переменная x2 | f0(x1, x2) = x2 | |
| f6 | Cложение по модулю два | f0(x1, x2) =  | |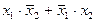
| f7 | Дизъюнкция | f0(x1, x2) = x1+x2 | |
| f8 | Стрелка Пирса | f0(x1, x2) =  | |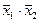
| f9 | Функция равнозначности | f0(x1, x2) =  | |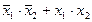
| f10 | Инверсия x2 | f0(x1, x2) =  | |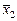
| f11 | Импликация от x1к x2 | f0(x1, x2) =  | |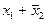
| f12 | Инверсия x1 | f0(x1, x2) =  | |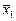
| f13 | Импликация от x2 к x1 | f0(x1, x2) =  | |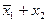
| f14 | Штрих Шеффера | f0(x1, x2) =  | |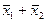
| f15 | Константа 1 | f0(x1, x2) = 1 |
Конституентой единицы называется такое логическое произведение (конъюнкция) п переменных одного набора, в которое каждая переменная входит только один раз в прямой или инверсной форме. Переменная, принимающая на данном наборе значение «1», записывается в конституенте единицы в прямом виде, а значение «0» – в инверсном виде.
Отличительной особенностью конституенты единицы является то, что она равна «1» только на одном вполне определенном наборе значений переменных. Будем обозначать конституенту единицы символом тi, где индекс i указывает на номер набора, на котором конституента единицы равна «1».
Например, для нулевого набора логических переменных (рисунок 5.4) конституента единицы имеет вид
,
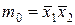
а для второго набора – соответственно вид
.
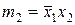
В общем случае можно записать 2 п конституент единицы, где п – число логических переменных в наборах.
Конституентой нуля п переменных одного набора называется логическое сложение (дизъюнкция) этих переменных, которое обращается в «0» лишь при одном наборе логических переменных. При этом в прямом виде в конституенте нуля записывают переменные, принимающие на данном наборе значение «0», а в инверсном – значение «1». Будем обозначать конституенту нуля символом рi, где индекс i указывает на номер набора, на котором конституента нуля равна «0». Например, для нулевого набора логических переменных (рисунок 5.4) конституента нуля имеет вид
,
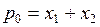
а для первого набора – соответственно вид
.
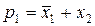
Аналитическая запись логической функции может быть выполнена в виде совершенной дизъюнктивной или совершенной конъюнктивной нормальной формы.
Совершенной дизъюнктивной нормальной формой(СДНФ) логической функции называется дизъюнкция всех конституент единицы для тех наборов логических переменных, на которых логическая функция принимает значение «1».
Запись СДНФ логической функции осуществляется непосредственно по данным, внесенным в таблицу истинности. Например, воспользовавшись рисунком 5.4, запишем СДНФ логической функции у:
. (5.1)
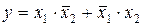
Совершенной конъюнктивной нормальной формой(СКНФ) логической функции называется конъюнкция всех конституент нуля для тех наборов логических переменных, на которых логическая функция принимает значение «0». Следовательно, для функции у (рисунок 5.4) СКНФ будет иметь вид
. (5.2)
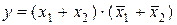
Тождественные преобразования логических функций для получения их оптимального вида осуществляют на основе законов и тождеств алгебры логики.