Что понимают под измерением метрология

Измерение

Измерение — совокупность операций для определения отношения одной (измеряемой) величины к другой однородной величине, принятой за единицу, хранящуюся в техническом средстве (средстве измерений). Получившееся значение называется числовым значением измеряемой величины, числовое значение совместно с обозначением используемой единицы называется значением физической величины. Измерение физической величины опытным путём проводится с помощью различных средств измерений — мер, измерительных приборов, измерительных преобразователей, систем, установок и т. д. Измерение физической величины включает в себя несколько этапов: 1) сравнение измеряемой величины с единицей; 2) преобразование в форму, удобную для использования (различные способы индикации).

Характеристикой точности измерения является его погрешность или неопределённость. Примеры измерений:

В тех случаях, когда невозможно выполнить измерение (не выделена величина как физическая, или не определена единица измерений этой величины) практикуется оценивание таких величин по условным шкалам, например, Шкала Рихтера интенсивности землетрясений, Шкала Мооса — шкала твёрдости минералов.

Наука, предметом изучения которой являются все аспекты измерений, называется метрологией.

Содержание

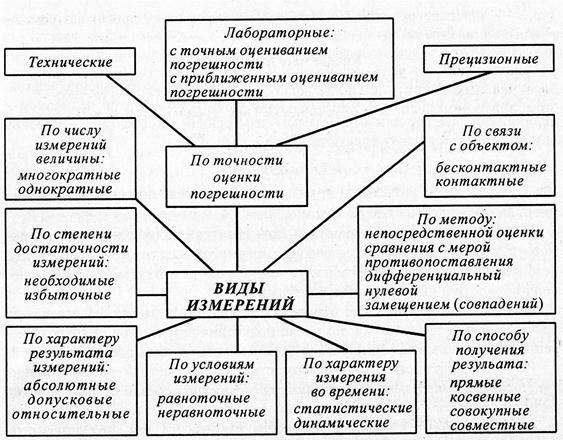
Классификация измерений

По видам измерений

Согласно РМГ 29-99 «Метрология. Основыне термины и определения» выделяют следующие виды измерений:

Также стоит отметить, что в различных источниках дополнительно выделяют таки виды измерений: метрологически и технические, необходимые и избыточные и др.

По методам измерений

По условиям, определяющим точность результата

По отношению к изменению измеряемой величины

Статические и динамические.

По результатам измерений

Классификация рядов измерений

По точности

По числу измерений

Классификация измеряемых величин

По точности

По результатам измерений

История

Единицы и системы измерения

См. также

Примечания

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

Полезное

Смотреть что такое «Измерение» в других словарях:

ИЗМЕРЕНИЕ — представление свойств реальных объектов в виде числовой величины, один из важнейших методов эмпирического познания. В самом общем случае величиной называют все то, что может быть больше или меньше, что может быть присуще объекту в большей или… … Философская энциклопедия

Измерение X — Измерение Икс … Википедия

измерение — замер, обмер; вымеривание, установление, фиксирование, замеривание, распознавание, промер, диагностирование, смеривание, нахождение, обмеривание, определение Словарь русских синонимов. измерение см. установление 2 Словарь синонимов … Словарь синонимов

измерение — (в психологии) научный метод представления числами интересующего психического свойства или параметров психического процесса на основе нек рых процедурных правил. Совокупность теоретико математических представлений и процедурных правил,… … Большая психологическая энциклопедия

ИЗМЕРЕНИЕ — ИЗМЕРЕНИЕ, измерения, ср. 1. Действие по гл. измерить измерять. Измерение роста. 2. Измеряемая величина, протяжение (мат.). Куб имеет три измерения: длину, высоту и ширину. ❖ Четвертое измерение (ирон.) перен. сверхъестественная и бесплодно… … Толковый словарь Ушакова

ИЗМЕРЕНИЕ — последовательность эксперим. и вычислит. операций, осуществляемая с целью нахождения значения физ. величины, характеризующей нек рый объект или явление. И. завершается определением степени приближения найденного значения к истинному значению… … Физическая энциклопедия

ИЗМЕРЕНИЕ — ИЗМЕРЕНИЕ, действия, производимые с целью нахождения числовых значений какой либо величины в принятых единицах измерения. Измерение выполняют с помощью соответствующих средств измерения (линейка, часы, весы и т.д.). Различают прямые… … Современная энциклопедия

ИЗМЕРЕНИЕ — совокупность действий, выполняемых при помощи средств измерений с целью нахождения числового значения измеряемой величины в принятых единицах измерения. Различают прямые измерения (напр., измерение длины проградуированной линейкой) и косвенные… … Большой Энциклопедический словарь

измерение — Сравнение конкретного проявления измеряемого свойства (измеряемой величины) со шкалой (частью шкалы) измерений этого свойства (величины) с целью получения результата измерения (значения величины или оценки свойства). [МИ 2365 96] измерение… … Справочник технического переводчика

Измерение — ИЗМЕРЕНИЕ, действия, производимые с целью нахождения числовых значений какой либо величины в принятых единицах измерения. Измерение выполняют с помощью соответствующих средств измерения (линейка, часы, весы и т.д.). Различают прямые… … Иллюстрированный энциклопедический словарь

Источник

Метрология: основные понятия и определения

Обновлено: 22 Мая 2021

Качество продукции всегда является основным критерием при выборе того или иного товара. Его обеспечивают три фундаментальных направления — метрология, стандартизация и сертификация.

Что такое метрология

Метрология присутствует во всех сферах жизни. Рождаясь, человек сразу сталкивается с измерениями — в роддоме отмечаются длина, масса и температура. В повседневной жизни от количественных оценок (температура воздуха, время суток) зависит деятельность, поведение человека. Метрология является базой для многих технических отраслей. Она вырабатывает показатели, на которые ориентируются при проведении технологических экспериментов, на производстве. Метрологическая отрасль выступает регулятором социально-экономических отношений в обществе.

Метрология (от греч. «метро» — мера и «логос» — учение) — наука, изучающая комплекс измерений, методику и способы обеспечения их точности.

Главным критерием результатов измерений является их единство. Под этим термином понимают установленные единицы величин измерений и заданные допустимые погрешности. Благодаря этому есть возможность сопоставлять результаты замеров, производимых в разных местах, в разное время и различными способами.

Предметом метрологии выступают:

Единство измерений регулируется законом РФ «Об обеспечении единства измерений». Он определяет метрологические службы, разграничивает сферы государственного контроля, указывает меру ответственности за нарушение метрологических требований.

Терминология в метрологии устанавливается правовым актом РМГ 29-2013.

Одним из основных в метрологической науке является понятие физической величины. Это свойство, общее для многих объектов в качественном отношении, но индивидуальное для каждого объекта по количественным показателям.

Размер физической величины — количественный показатель свойства физической величины.

Средство измерений — техническое средство, которое имеет соответствующие нормам характеристики и применяется для снятия замеров.

Результат измерения — количественное значение физической величины, полученное в результате практических опытов.

Точность средства измерения — качественная характеристика, которая отражает близость погрешности измерения по отношению к нулю.

Разделы метрологии

Структура метрологии состоит из трех разделов:

Виды и методы измерений

Цель измерения состоит в извлечении значения в той форме, которая наиболее удобна для использования.

Виды измерений классифицируют по различным признакам:

1. По показателю точности:

2. По численности замеров:

3. В зависимости от изменений величины, которая измеряется:

4. В зависимости от выражения результата измерений:

5. В зависимости от способов получения замеров:

Метод измерений — комплекс сравнительных приемов измеряемой величины с ее единицей соответственно с используемым принципом измерения.

Классификация методов зависит от признаков:

1. По приемам достижения результата замеров:

3. По способу сопоставления измеряемой величины с её единицей:

Метод сравнения с мерой, в свою очередь, делится на виды:

Классификация средств измерений

Средства измерения (СИ) классифицируются в зависимости от:

По способам конструктивной реализации СИ разделяют на:

Меры величины — это фиксированные СИ, которые неоднократно используются. Они делятся на:

До начала использования каждый стандартный образец проходит метрологическую аттестацию. В зависимости от уровня использования выделяют государственные, отраслевые, межгосударственные СО и СО предприятий.

Среди измерительных преобразователей выделяют:

Измерительные приборы являются СИ с фиксированным диапазоном. Различают:

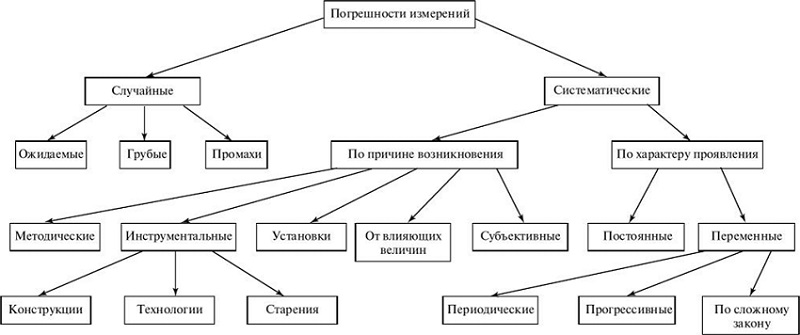
Классификация погрешностей

Погрешность измерения — несоответствие результата измерения Х истинному значению Хи:

Классификация погрешностей формируется на основе:

1. Способа выражения:

2. Источника выражения:

3. Закономерностей возникновения или проявления:

Согласно соотношению положительных отзывов, специалисты сервиса Феникс.Хелп не допускают погрешностей в выполнении курсовых и контрольных работ для студентов.

Источник

Лекция 2. Виды и методы измерений

Описание

1. Основные понятия и определения. Виды измерений.

2. Методы измерений.

3. Понятие о точности измерений.

4. Основы обеспечения единства измерений

Оглавление

1. Основные понятия и определения. Виды измерений

Измерение — совокупность операций по применению системы измерений для получения значения измеряемой физической величины.

Измерения могут быть классифицированы по метрологическому назначению на три категории:

Ненормированные – измерения при ненормированных метрологических характеристиках.

Технические – измерения при помощи рабочих средств измерений.

Метрологические – измерения при помощи эталонов и образцовых средств измерений.

Ненормированные измерения наиболее простые. В них не нормируются точность и достоверность результата. Поэтому область их применения ограничена. Они не могут быть применены в области, на которую распространяется требование единства измерений. Каждый из нас выполнял ненормированные измерения длины, массы, времени, температуры не задумываясь о точности и достоверности результата. Как правило, результаты ненормированных измерений применяются индивидуально, т.е. используются субъектом в собственных целях.

Технические измерения удовлетворяют требованиям единства измерений, т.е. результат бывает получен с известной погрешностью и вероятностью, записывается в установленных единицах физических величин, с определённым количеством значащих цифр. Выполняются при помощи средств измерений с назначенным классом точности, прошедших поверку или калибровку в метрологической службе. В зависимости от того, предназначены измерения для внутрипроизводственных целей или их результаты будут доступны для всеобщего применения, необходимо выполнение калибровки или поверки средств измерений. Средство измерений, прошедшее калибровку или поверку, называют рабочим средством измерений. Примером технических измерений является большинство производственных измерений, измерение квартирными счётчиками потреблённой электроэнергии, измерения при взвешивании в торговых центрах, финансовые измерения в банковских терминалах. Средство измерений, применяемое для калибровки других средств измерений, называют образцовым средством измерений. Образцовое средство измерений имеет повышенный класс точности и хранится отдельно, для технических измерений не применяется.

Метрологические измерения не просто удовлетворяют требованиям единства измерений, а являются одним из средств обеспечения единства измерений. Выполняются с целью воспроизведения единиц физических величин для передачи их размера образцовым и рабочим средствам измерений. Метрологические измерения выполняет метрологическая служба в стандартных условиях, сертифицированным персоналом.

В дисциплине «Метрология, стандартизация и сертификация» рассматриваются технические измерения.

Можно выделить следующие виды измерений.

1) По характеру зависимости измеряемой величины от времени методы измерений подразделяются на:

2) По способу получения результатов измерений (виду уравнений измерений) методы измерений разделяют на прямые, косвенные, совокупные и совместные.

При прямом измерении искомое значение величины находят непо­средственно из опытных данных (например, измерение диаметра штан­генциркулем).

При косвенном измерении искомое значение величины определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям.

Совместными называют измерения двух или нескольких не одноимённых величин, производимые одновременно с целью нахождения функциональной зависимости между величинами (например, зависимости длины тела от температуры).

Совокупные – это такие измерения, в которых значения измеряемых величин находят по данным повторных измерений одной или нескольких одноименных величин (при различных сочетаниях мер или этих величин) путем решения системы уравнений.

3) По условиям, определяющим точность результата измерения, мето­ды делятся на три класса.

Измерении максимально возможной точности (например, эталонные измерения), достижимой при существующем уровне техники.

Контрольно-поверочные измерения, погрешность которых с определенной вероятностью не должна превышать некоторое заданное значение.

Технические измерения, в которых погрешность результата определяется характеристиками средств измерения.

4) По способу выражения результатов измерений различают абсолютные и относительные измерения.

Абсолютное измерение основано на прямых измерениях величины и (или) использования значений физических констант.

При относительных измерениях величину сравнивают с одноименной, играющей роль единицы или принятой за исходную (например, измерение диаметра вращающейся детали по числу оборотов соприкасающегося с ней аттестованного ролика).

5) В зависимости от совокупности измеряемых параметров изделия различают поэлементный и комплексный методы измерения.

Поэлементный метод характеризуется измерением каждого параметра изделия в отдельности (например, эксцентриситета, овальности, огранки цилиндрического вала).

Комплексный метод характеризуется измерением суммарного пока­зателя качества (а не физической величины), на который оказывают влияние отдельные его составляющие (например, измерение радиального биения цилиндрической детали, на которое влияют эксцентриситет, овальность и др.).

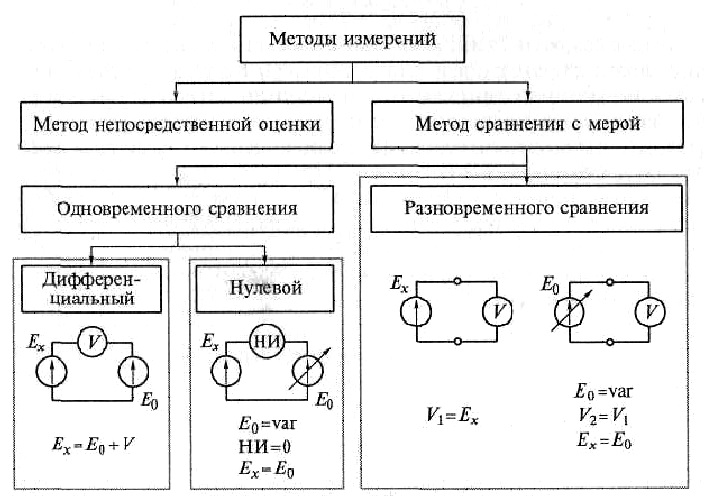
2. Методы измерений

Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализо­ванным принципом измерений. Можно выделить следующие методы из­мерений.

По способу получения значения измеряемых величин различают два основных метода измерений.

Метод непосредственной оценки – метод измерения, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора прямого действия.

Метод сравнения с мерой – метод измерения, при котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.

Разновидности метода сравнения:

При измерении линейных величин независимо от рассмотренных методов различают контактный и бесконтактный методы измерений.

В зависимости от измерительных средств, используемых в процессе измерения, различают:

3. Понятие о точности измерений

Точность результата измерения – характеристика качества измерения, отражающая близость к нулю погрешности его результата.

Эти погрешности являются следствием многих причин: несовершенства средств измерений, метода измерений, опыта оператора; недостаточной тщательности проведения измерения; воздействия внешних условий и т.д. Для оценки степени приближения результатов измерения к истинному значению измеряемой величины используются методы теории вероятности и математической статистики, что позволяет с определенной достоверностью оценить границы погрешностей, за пределы которых они не выходят. Это дает возможность для каждого конкретного случая выбрать средства и методы измерения, обеспечивающие измерение результата, погрешности которого не превышают заданных границ с требуемой степенью доверия к результатам измерений (достоверностью).

Класс точности – обобщённая метрологическая характеристика средства измерения.

Класс точности определяется и обозначается по-разному. Наибольшее распространение получили три варианта, каждый представляет собой выраженное в процентах значение относительной погрешности:

– относительно измеренного значения (относительная погрешность),

– относительно максимального значения шкалы (приведённая погрешность),

– относительно участка шкалы (приведённая к участку шкалы погрешность).

Рассмотрим эти три варианта.

Вариант 1. Относительная погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, результат измерения умножают на класс точности и делят на сто, чтобы избавиться от процентов. Например, вольтметром класса точности 0,1 получено значение 10,000 В.

Абсолютная погрешность составит: (10,000 В ∙ 0,1 %) / 100 % = 0,010 В. Запись результата: (10,000 ± 0,010) В, с вероятностью 95 % (эта вероятность по умолчанию назначается для технических измерений, исходя из этой вероятности определяется и класс точности). При нормировании по относительной погрешности, значение класса точности заключают в кружок. Как правило, обозначение класса точности размещают в правом нижнем углу на шкале средства измерений.

Вариант 2. Приведённая погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, максимальное значение шкалы умножают на класс точности и делят на сто, чтобы избавиться от процентов. Например, вольтметром класса точности 0,1 получено значение 10,000 В. Максимальное значение шкалы составляет 20,000 В.

Абсолютная погрешность составит: (20,000 В ∙ 0,1 %) / 100 % = 0,020 В. Запись результата: (10,000 ± 0,020) В, с вероятностью 95 %. При нормировании по приведённой погрешности, значение класса точности не сопровождают никакими знаками.

Вариант 3. Приведённая к участку шкалы погрешность.

Чтобы по классу точности определить значение абсолютной погрешности, размер участка шкалы умножают на класс точности и делят на сто, чтобы избавиться от процентов. Рассмотрим два примера, для случая, когда вся шкала поделена на два участка.

Пример 1. Участок шкалы от 0,000 В до 12,000 В, отмечен галочкой. Вольтметром класса точности 0,1 получено значение 10,000 В.

Абсолютная погрешность составит: (12,000 В ∙ 0,1 %) / 100 % = 0,012 В. Запись результата: (10,000 ± 0,012) В, с вероятностью 95 %.

Пример 2. Участок шкалы от 12,000 В до 20,000 В, также отмечен галочкой. Вольтметром класса точности 0,1 получено значение 15,000 В.

Абсолютная погрешность составит: (8,000 В ∙ 0,1 %) / 100 % = 0,008 В. Запись результата: (15,000 ± 0,008) В, с вероятностью 95 %. При нормировании по приведённой к участку шкалы погрешности, значение класса точности помещают над галочкой. Участки шкалы, относительно которых нормируется погрешность, обозначают галочками.

Варианты классов точности обусловлены отличием конструктивных, системных и схемотехнических решений средств измерений.

Корректная запись результатов

Запись результатов измерений производится по следующим правилам.

1) Погрешность указывается двумя значащими цифрами, если первая равна 1 или 2. Погрешность указывается одной значащей цифрой, если первая равна 3 или более. Все остальные цифры должны быть не значащими.

Значащей цифрой называется любая цифра числа, записанного в виде десятичной дроби, начиная слева с первой отличной от нуля цифры, независимо от того, где она находится – до запятой или после запятой.

2) Результат измерения округляется в соответствии с его погрешностью, т.е. записывается с той же точностью, что и погрешность.

Рассмотрим пример. Результат измерения: 10,645701, погрешность 0,012908.

1) Рассматриваем погрешность. Первая значащая цифра 1, поэтому оставляем две значащие цифры, округляя, записываем: 0,013.

2) Рассматриваем результат измерения. Погрешность записана с точностью до третьего знака после запятой, поэтому в результате также оставим три знака. Округляя, записываем: 10,646.

Корректная запись: 10,646 ± 0,013.

Корректная запись обеспечивает адекватность и сопоставимость результатов различных измерений и является одним из элементов единства измерений. Как правило, отбрасывание избыточных цифр не приводит к дополнительной погрешности, поскольку избыточные цифры обусловлены точностью вычислений, а не точностью измерений.

4. Основы обеспечения единства измерений

Специализация и кооперирование производства в масштабах страны, основанные на принципах взаимозаменяемости, требуют обеспечения и сохранения единства измерений.

Обеспечение единства измерений – деятельность метрологических служб, направленная на достижение и поддержание единства измерений в соответствии с правилами, требованиями и нормами, установленными государственными стандартами и другими нормативно-техническими документами в области метрологии.

В 1993 г. был принят Закон Российской Федерации «Об обеспечении единства измерений», который устанавливает правовые основы обеспечения единства измерений в нашей стране. Он состоит из семи разделов: общие положения; единицы величин, средства и методики выполнения измерений; метрологические службы; государственный метрологический контроль и надзор; калибровка и сертификация средств измерений; ответственность за нарушение закона и финансирование работ по обеспечению единства измерений. В Законе дано следующее определение понятия «единство измерения»:

«Единство измерения – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерений не выходят за установленные границы с заданной вероятностью».

Обеспечение единства измерений является задачей метрологических служб.

Метрологическая служба – совокупность субъектов, деятельности и видов работ, направленных на обеспечение единства измерений.

Закон определяет, что Государственная метрологическая служба находится в ведении Госстандарта России и включает: государственные научные метрологические центры; органы Государственной метрологической службы регионов страны, а также городов Москва и Санкт-Петербург.

Источник

Основные понятия и термины метрологии. Измерения. Принципы и методы измерений

Различают теоретическую метрологию, законодательную метрологию и практическую метрологию.

Таким образом, чтобы понять, чем собственно занимается метрология, нам, прежде всего, необходимо разобраться с тем, что же будем называть измерением и что такое точность измерений.

Вопрос о точности измерений мы рассмотрим в следующей лекции, а сейчас попробуем понять, что такое измерение.

Любой человек в процессе своей жизни непрерывно сравнивает различные объекты между собой или с некоторыми моделями этих объектов, которые хранятся в его памяти. Мы «узнаём» человека сравнив его с образом этого человека в нашей памяти. Сравнив объекты между собой, мы, например, можем сказать, что данные предметы одинаковы или что один объект больше другого. Измерение, а при изучении метрологии мы будем заниматься именно измерениями, это также прежде всего сравнение. Например, измеряя длину, мы сравниваем объект с некоторой мерой длины.

Давайте попробуем разобраться в том, как мы сравниваем объекты между собой, а заодно и договоримся при каких условиях такое сравнение мы будем считать измерением.

Если мы видим перед собой два автомобиля одной и той же марки и одного и того же цвета, мы уверенно говорим, что они одинаковы. Запомнив лицо человека мы, встретив его на улице, «узнаём» его.

Как происходит сравнение? Оказывается мы иногда осознанно, а иногда на интуитивном уровне определяем множество свойств, присущих данным объектам, выделяем те из них, которые по нашему мнению являются наиболее важными, сравниваем эти свойства между собой и, если при сравнении они признаются одинаковыми, делаем вывод об «одинаковости» сравниваемых объектов.

Если при этом вероятность наличия «одинаковых» по свойствам, но различных объектов меньше некоторого уровня (условно его можно назвать уровнем достоверности), мы «узнаём» объект.

Например, сравнивая два камня, мы проверяем одинакового ли они цвета, размера, веса, формы, твёрдости и т.п. Если все эти свойства одинаковы, мы говорим, что перед нами два одинаковых камня. Если мы сравниваем камень не с другим камнем, а с описанием его свойств, мы можем также сделать вывод о том, что перед нами именно тот, исходный камень. Мы его «узнаём».

Примечание:Если сравнивать алмаз в 198 карат с описанием алмаза «Орлов», венчающего скипетр Российских императоров, и некоторый не очень большой перечень свойств сравниваемого алмаза совпадает с соответствующими свойствами алмаза «Орлов», то, поскольку наличие второго такого алмаза крайне мало вероятно, постольку можно признать, что это и есть алмаз «Орлов». Если же перед нами кусок гранита, то для признания его именно тем самым куском гранита потребуется сравнение гораздо большего числа свойств, т.к. вероятность наличия «похожих» кусков гранита существенно больше.

Итак мы, сравнивая объекты между собой или с их «моделями» в нашей памяти, на самом деле сравниваем свойства этих объектов.

Но у объекта, вообще говоря, может быть бесконечно много свойств. Мы просто физически не сможем все их сравнить между собой (запомнить в памяти).

Поэтому некоторые свойства мы относим к атрибутам объекта (необходимое, существенное, неотъемлемое свойство предмета или явления), а некоторые к второстепенным.

Чаще всего, мы и ограничиваемся сравнением только атрибутов объектов. В частности, наличие одинаковых атрибутов марки и цвета позволяет нам сделать вывод об одинаковости двух разных автомобилей, но на самом деле значение имеет и год их выпуска, и степень изношенности двигателя, и кто и когда занимался их сборкой, кто и сколько их эксплуатировал и т.п.

Платон

Диоген

Рассмотрим теперь такое широко используемое в метрологии понятие как «Шкала измерений». В РМГ 83-2007[3] понятие шкалы измерений определено следующим образом:

Шкала (измерений): Отображение множества различных проявлений количественного или качественного свойства на принятое по соглашению упорядоченное множество чисел или другую систему логически связанных знаков (обозначений).

Примечание: Шкала от лат. scala — лестница.

Другими словами, вводя понятие шкалы мы утверждаем, что в большинстве случаев мы сравниваем не непосредственно свойства интересующих нас объектов, а отображения их свойств на некоторое множество возможных значений этого свойства, на шкалу измерений. Затем мы сравниваем уже эти отображения между собой и, если они одинаковы, считаем одинаковыми свойства объектов.

Примечание: Если мы определяем цвет объектов по шкале цветов, имеющей, например, всего семь цветов радуги, то вероятность того, что цвета сравниваемых объектов мы посчитаем одинаковыми гораздо выше такой же вероятности при наличии в шкале цветов 16777216 (режим TRUE COLOR экрана монитора) цветов и оттенков, т.е. признание одинаковости объектов зависит от детальности принятой шкалы наименований.

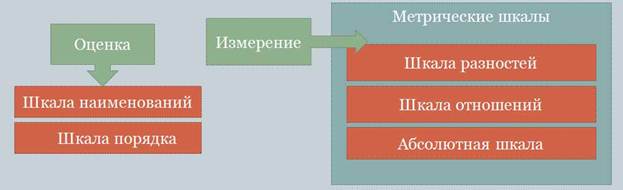
Различают пять основных типов шкал: наименований, порядка, разностей (интервалов), отношений и абсолютные (Далее термины, касающиеся шкал измерений по РМГ 83-2007).

Шкала наименований: Шкала измерений качественного свойства, характеризующаяся только соотношениями эквивалентности или отличиями проявлений этого свойства.

Цветовая гамма RAL

Другими словами, используя шкалу наименований мы можем классифицировать объекты по эквивалентности их свойств.

Примером такой шкалы наименований является шкала цветов RAL[6]. По этой шкале мы определяем цвета сравниваемых объектов сравнивая их с некоторой палитрой цветов и, если результаты сравнения совпали, утверждаем, что объекты имеют одинаковый цвет.

С математической точки зрения вводя шкалу наименований мы всё множество объектов разбиваем на непересекающиеся подмножества и присваиваем каждому такому подмножеству некоторое наименование.

В шкалах наименований отсутствует понятия нуля, «меньше», «больше» и единицы измерения.

Шкала порядка: Шкала измерений количественного свойства (величины), характеризующаяся соотношениями эквивалентности и порядка по возрастанию (убыванию) различных проявлений свойства.

Другими словами, кроме разбивания множества объектов на подмножества и присвоения каждому подмножеству наименования мы определяем отношения больше или меньше среди этих подмножеств. Но мы с помощью такой шкалы не можем определить насколько больше или меньше рассматриваемое свойство у разных объектов.

В шкалах порядка не обязательно наличие понятия нуля, существует понятия «меньше», «больше», но нет понятия единицы измерения.

Шкала разностей [интервалов]: Шкала измерений количественного свойства (величины), характеризующаяся соотношениями эквивалентности, порядка, суммирования интервалов различных проявлений свойства.

Шкала разности состоит из одинаковых интервалов и произвольно выбранной нулевой точки.

Например, к такой шкале относится система летосчисления. В качестве интервала в такой шкале используется год, а за нулевую точку принимают или сотворение мира[8], или рождение Христа или, например, момент хиджры (переезда) Пророка Мухаммада из Мекки в Ясриб (Медину)[9].

Ещё одним примером шкал разности могут быть температурные шкалы Цельсия и Фаренгейта[10].

Главным отличием шкалы интервалов от шкалы разностей можно считать аддитивность её интервалов. Например, зная сколько лет прошло от начала летоисчисления до начала Северной войны и сколько лет прошло с начала Северной войны до основания Санкт-Петербурга можно сложить два этих интервала и узнать сколько лет прошло от начала летоисчисления до основания Санкт-Петербурга.

Шкала отношений: Шкала измерений количественного свойства(величины), характеризующаяся соотношениями эквивалентности, порядка, пропорциональности (допускающими в ряде случаев операцию суммирования) различных проявлений свойства.

В шкалах отношений, помимо свойств имеющихся у шкал разностей добавляется наличие естественного нуля и устанавливаемой по соглашению единицы измерений.

Примером шкалы отношений может быть, например, шкала массы.

Фактически шкала отношений это шкала интервалов с естественным нулём. При использовании шкалы отношений измерение это определение отношения измеряемой величины к другой подобной, принятой за единицу.

Абсолютная шкала: Шкала отношений (пропорциональная или аддитивная) безразмерной величины.

Примером абсолютной шкалы может быть шкала учёта количества единиц произведённой продукции, количество проведённых экспериментов и т.п. При таких измерениях на измерительной шкале отмечаются абсолютные количественные значения измеряемого.

Пример: Количество подсчитанных баранов в штуках

Шкалы разностей, отношений, а иногда и абсолютная шкала обычно объединяют термином «метрические шкалы».

Понятие«единица измерений» не имеет смысла для свойств, описываемых шкалами наименований и порядка.

Размер единиц измерений величин, описываемых абсолютными шкалами, однозначно определяется безразмерным характером измеряемых величин.

Как мы уже отмечали, любое измерение это сравнение. В тоже время даже на интуитивном уровне мы понимаем, что не всякое сравнение можно считать измерением. Например, глядя на двух стоящих рядом человек, мы как правило достаточно уверено отвечаем на вопрос о том, кто из них красивее. Но совершенно очевидно, что мы при этом не измеряем «красоту» человека.

Будем считать, что сравнение является измерением, если при сравнении используются метрические шкалы. В остальных случаях будем говорить об оценке свойств объектов.

Примечание:Оценка свойства: Выражение местоположения качественного свойства конкретного объекта измерений на соответствующей шкале наименований[3]. (Иногда и шкале порядка).

Теперь у нас есть критерий, с помощью которого можно понять является ли данное сравнение измерением или это только оценка свойства объекта. Однако строгое определение понятия «измерение» дать не так просто.

Ниже, в частности, приводятся различные определения понятия «измерение», взятые из литературы и нормативных документов разных лет.

— Измерением называется познавательный процесс, заключающийся в сравнении путем физического эксперимента данной величины с некоторым ее значением, принятым за единицу сравнения ([9].).

— Измерение— совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины[2].

— Измерение— совокупность операций, имеющих целью определить значение величины[11].

Не претендуя на исключительную истину, будем, тем не менее, в дальнейшем пользоваться определением, данным в [2].

Измерение— совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.

Приведенные выше определения измерения могут быть выражены уравнением, которое мы уже приводили при рассмотрении первого вопроса и которое в метрологии называется основным уравнением измерений:

Объект, свойства которого мы собираемся измерять будем называть объектом измерения.

Например, объектом измерения может быть: коленчатый вал, у которого измеряют диаметр; технологический процесс, во время которого измеряют температуру; спутник Земли, координаты которого измеряются. Это все объекты измерения.

Для описания порядка проведения измерений в метрологии используются понятия принципа измерения, метода и методики измерения. Рассмотрим их подробнее.

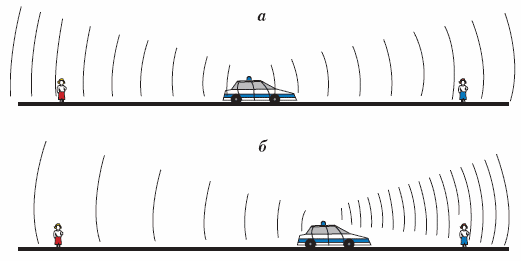
Например, для измерения скорости объекта можно использовать «Эффект Доплера», заключающийся в том, что при движении объекта изменяется частота и длина волны, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Измеряя эти изменения можно определить скорость движущегося предмета. Это принцип измерения скорости.

Для метода измерения, который чаще всего, рассматривается как уточнение, детализация и конкретизация принципа измерения, существует несколько в общем-то отличающихся друг от друга определений. Например:

Если в «Международном словаре по метрологии: основные и общие понятия и соответствующие термины»[4] это в каком-то смысле алгоритм реализации принципа измерения, то в «РМГ 29-99 РЕКОМЕНДАЦИИ ПО МЕЖГОСУДАРСТВЕННОЙ СТАНДАРТИЗАЦИИ. Государственная система обеспечения единства измерений. МЕТРОЛОГИЯ. Основные термины и определения»[8] метод это «приём или совокупность приёмов», что в общем случае не совсем одно и тоже.

Однако, как правило, это не приводит к непониманию, так как и там и там метод это, прежде всего, описание того, как с использованием выбранного принципа можно провести желаемое измерение.

Рис.1. Эффект Доплера: а – два наблюдателя слышат звук сирены неподвижной машины одинаково; б – наблюдатель, к которому приближается машина, слышит звук более высокой частоты, а наблюдатель, от которого удаляется машина, – звук более низкой частоты

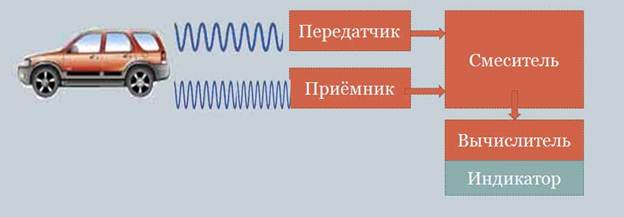
Например, для реализации принципа измерения с помощью эффекта Доплера может, в частности, использоваться Доплеровский измеритель скорости, который содержит передатчик (источник излучаемых радиоволн), антенну с направленным излучением радиоволн, приёмник отражённых от объекта волн, смеситель – устройство для выделения доплеровской частоты – вычислитель и индикаторное устройство (собственно измеритель).

Рис.2. Метод измерения скорости транспортных средств с помощью Эффекта Доплера

Передатчик излучает радиоволны определённой частоты. Отражённые от объекта радиоволны принимает приёмник. В зависимости от скорости и направления движения транспортного средства их частота изменяется. На выход смесителя поступает сигнал с частотой, равной разности излучаемого и принимаемого сигнала. По этой разности вычислитель определяет скорость объекта, значение которой индицируется на индикаторе.

Таким образом, методика измерений это дальнейшая конкретизация метода. Методика измерений обычно описывается в инструкции по использованию конкретного измерительного прибора.

Рис.3. Измерение скорости с помощью доплеровского радара

Примечание:

Кристиан Доплер 29 ноября 1803, Зальцбург — 17 марта 1853, Венеция) — австрийский физик. В 1825 году окончил Политехнический институт в Вене, с 1835 по 1847 год работал в Чешском техническом университете, с 1847 года — профессор Горной и Лесной академий в Хемнице, с 1848 года — член Венской Академии Наук, с 1850 — профессор Венского университета и директор первого в мире Физического института, созданного при Венском университете по его инициативе. В 1842 Доплер теоретически обосновал зависимость частоты колебаний, воспринимаемых наблюдателем, от скорости и направления движения источника волн и наблюдателя относительно друг друга. Это явление впоследствии было названо его именем (эффект Доплера).

За время существования метрологии или, если точнее, за всё время с того момента, когда первые люди стали что-то измерять и до наших дней, были разработаны сотни, а может быть даже тысячи различных принципов измерения и десятки тысяч различных методов измерения.

Естественно возникает желание как-то упорядочить эти известные методы, классифицировать их, найти в них что-то общее, вычленить информацию, которую можно было бы использовать при разработке новых методов.

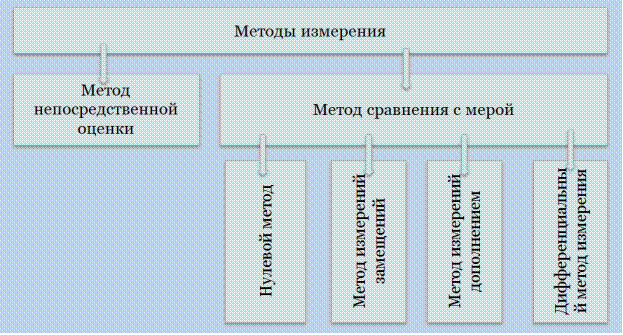
Классификация методов измерений[2] показана на рис.4. Прежде всего все методы измерений делятся на методы непосредственной оценки и методы сравнения с мерой.

Например, взвешивание на циферблатных весах или измерение давления пружинным манометром.

Метод сравнения с мерой— метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой[8].

Группа методов сравнения с мерой включает в себя следующие методы: нулевой, замещения, дополнением и дифференциальный.

Рис.4. Классификация методов измерения

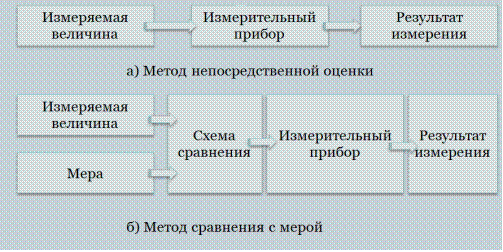
Фактически разница между методом непосредственной оценки и методами сравнения с мерой не такая уж и большая. Как и при методе сравнения с мерой при использовании метода непосредственной оценки измеряемая величина фактически сравнивается с мерой[11]. Просто при использовании метода непосредственной оценки эта мера «хранится» в измерительном приборе, с помощью которого проводится измерение, а при использовании метода сравнения с мерой используется внешняя по отношению к этому устройству мера. Именно за счёт использования внешней меры методы сравнения с мерой по сравнению с методами непосредственной оценки более точны, но несколько более сложны.

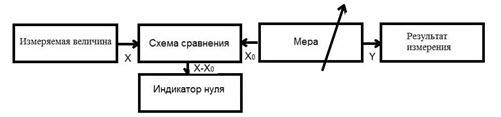
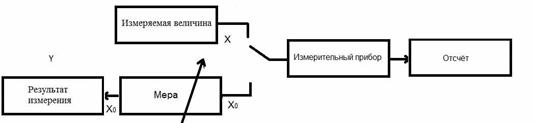
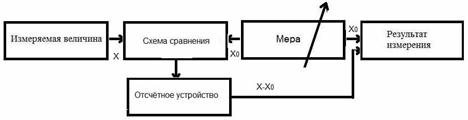
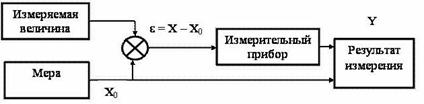
Рис.5. а) Схема измерения при использовании метода непосредственной оценки; б) Схема измерения при использовании метода сравнения с мерой.

Нулевой, дифференциальный и метод замещения реализуют различные способы сравнения с мерой.

Рис.6. Нулевой метод измерений

С помощью регулировки меры величина, поступающая от меры, и измеряемая величина уравниваются. Величина установленная мерой считается результатом измерения.

Примером использования нулевого метода измерений может быть измерение массы на равноплечных весах при помощи гирь.

Рис.7. Метод измерений замещением

Например, при взвешивании поочередным помещением массы и гирь на одну и ту же чашку весов.

Рис.8. Метод измерений дополнением

Метод измерений дополнением— метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению[8]

Рис.9. Дифференциальный метод измерений

В настоящее время не существует общепризнанной классификации видов измерений (термин виды, также не имеет строгого формального определения).

Например, в [12] разные виды измерений соответствуют измерению величин различного рода: измерения геометрических величин; измерения механических величин; измерения параметров потока, расхода, уровня, объема веществ; измерения давления, вакуумные измерения; измерения физико-химического состава и свойств веществ; теплофизические и температурные измерения; измерения времени и частоты». Один из вариантов такой классификации приведён, в частности, в учебнике «Метрология и радиоизмерения» под редакцией В.И. Нефедова, который мы рекомендуем Вам в качестве основного учебника по данной дисциплине[13].

Рис.4. Классификация видов измерений

Поэтому мы не будем здесь заниматься тонкостями такой классификации. Однако некоторые понятия, определяющие особенности измерений при решении различных практических задач и понимание которых необходимо при изучении данной дисциплины мы сейчас рассмотрим.

Во-первых, измерения подразделяются на прямые и косвенные.

Например, измерение силы тока амперметром или измерение массы на весах это прямые измерения.

Например, косвенным является измерение плотности D тела цилиндрической формы по результатам прямых измерений массы т, высоты h и диаметра цилиндра d. Для того, чтобы получить результат измерения необходимо вычислить объем цилиндра и разделить на полученное значение массу цилиндра.

Измерения бывают статическими и динамическими.

Примером статического измерения может быть измерение длины детали при нормальной температуре, измерение размеров земельного участка и т.п.

Строго говоря, все физические величины подвержены тем или иным изменениям во времени. В этом убеждает применение все более и более чувствительных средств измерений, которые дают возможность обнаруживать изменение величин, ранее считавшихся постоянными, поэтому разделение измерений на динамические и статические является условным

Кроме того в метрологии часто используются следующие понятия:

Совокупные измерения –проводимые одновременно измерения нескольких одноименных величин, при котором искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. При этом для определения значений искомых величин число уравнений должно быть не меньше числа величин. Примером совокупных измерений являются измерения, когда значение массы отдельных гирь из набора определяют по известному значению массы одной из гирь и по результатам измерений масс различных сочетаний гирь[14].

Совместные измерения – проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними[14].

Кроме того различают абсолютные и относительные измерения.

Абсолютное измерение– измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Например, измерение силы F = mg основано на измерении основной величины – массы m и использовании физической постоянной g[14].

Относительное измерение– измерение отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную. Например, измерение активности радионуклида в источнике по отношению к активности радионуклида в однотипном источнике, аттестованной в качестве эталонной меры активности. Существуют и другие классификации измерений, например, по связи с объектом (контактные и бесконтактные), по условиям измерений (равноточные и неравноточные)[14].

Следует также различать понятия измерение и наблюдение.

Источник