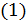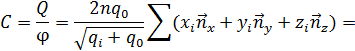Что принимается за электрическую постоянную
Электрическая постоянная
Электри́ческая постоя́нная (ранее также носила название диэлектрической постоянной) — физическая константа, скалярная величина,
Иногда, используя устаревшую терминологию, называют диэлектрической проницаемостью вакуума. Измеряется в фарадах на метр. Электрическая постоянная равна:
Ф/м.
Через электрическую постоянную осуществляется связь между относительной и абсолютной диэлектрической проницаемостью. Она также входит в запись закона Кулона:
См. также
Примечания
Полезное
Смотреть что такое «Электрическая постоянная» в других словарях:
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (e0) (по старой терминологии диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур ний в рационализованной форме, в соответствии с к рой образованы электрич. и магн. ед … Физическая энциклопедия
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
Полезное
Смотреть что такое «ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ» в других словарях:
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (см.) … Большая политехническая энциклопедия
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — постоянная электрическая (см.).
Смотреть что такое «ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ» в других словарях:
ЭЛЕКТРИЧЕСКАЯ ПОСТОЯННАЯ — (e0) (по старой терминологии диэлектрич. проницаемость вакуума), физ. постоянная, входящая в ур ния законов электрич. поля (см. КУЛОНА ЗАКОН) при записи этих ур ний в рационализованной форме, в соответствии с к рой образованы электрич. и магн. ед … Физическая энциклопедия
электрическая постоянная — Коэффициент, применяемый при записи ряда соотношений в СИ, равный величине, обратной произведению магнитной постоянной на квадрат скорости света в пустоте. Примечание — Электрическая постоянная приблизительно равна 8,85419 • 10 12 Ф/м … Справочник технического переводчика
электрическая постоянная — электрическая постоянная; отрасл. диэлектрическая проницаемость пустоты Скалярная величина, характеризующая электрическое поле в пустоте, равная отношению суммарного электрического заряда, заключенного внутри некоторой замкнутой поверхности, к… … Политехнический терминологический толковый словарь
Электрическая постоянная — (ранее также носила название диэлектрической постоянной) физическая константа, скалярная величина, определяющая напряжённость электрического поля в вакууме; входящая в выражения некоторых законов электромагнетизма, в том числе закона Кулона … Википедия
электрическая постоянная — elektrinė konstanta statusas T sritis automatika atitikmenys: angl. electric constant; permittivity constant; permittivity of free space; permittivity of vacuum vok. dielektrische konstante, f; Dielektrizitätskonstante, f; elektrische… … Automatikos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. electric constant; permittivity of vacuum vok. absolute Dielektrizitätskonstante, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
электрическая постоянная — elektrinė konstanta statusas T sritis fizika atitikmenys: angl. permittivity constant; permittivity of free space; permittivity of vacuum vok. Dielektrizitätskonstante, f; elektrische Feldkonstante, f; Verschiebungskonstante, f rus. абсолютная… … Fizikos terminų žodynas
Основные электрические величины
Рассмотрим основные электрические величины, которые мы изучаем сначала в школе, затем в средних и высших учебных заведениях. Все данные для удобства сведем в небольшую таблицу. После таблицы будут приведены определения отдельных величин, на случай возникновения каких-либо непониманий.
Существуют десятичные приставки, которые используются в названии величины и служат для упрощения описания. Самые распространенные из них: мега, мили, кило, нано, пико. В таблице приведены и остальные приставки, кроме названных.
Сила электрического тока в 1А – это величина, равная отношению заряда в 1 Кл, прошедшего за 1с времени через поверхность (проводник), к времени прохождения заряда через поверхность. Для протекания тока необходимо, чтобы цепь была замкнутой.
Сила тока измеряется в амперах. 1А=1Кл/1c
В практике встречаются
Электрическое напряжение – разность потенциалов между двумя точками электрического поля. Величина электрического потенциала измеряется в вольтах, следовательно, и напряжение измеряется в вольтах (В).
1Вольт – напряжение, которое необходимо для выделения в проводнике энергии в 1Ватт при протекании по нему тока силой в 1Ампер.
Единица измерения напряжения электрического тока представляет собой следующее отношение 1В=1Вт/1А.
В практике встречаются следующие варианты единиц измерения электрического потенциала, а точнее разности потенциалов:
Электрическое сопротивление – характеристика проводника препятствовать протеканию по нему электрического тока. Определяется как отношение напряжения на концах проводника к силе тока в нем. Измеряется в омах (Ом). В некоторых пределах величина постоянная.
1Ом – сопротивление проводника при протекании по нему постоянного тока силой 1А и возникающем при этом на концах напряжении в 1В.
Из школьного курса физики все мы помним формулу для однородного проводника постоянного сечения:
R=ρlS – сопротивление такого проводника зависит от сечения S и длины l
где ρ – удельное сопротивление материала проводника, табличная величина.
Между тремя вышеописанными величинами существует закон Ома для цепи постоянного тока.
Ток в цепи прямо пропорционален величине напряжения в цепи и обратно пропорционален величине сопротивления цепи – закон Ома.
Электрической емкостью называется способность проводника накапливать электрический заряд.
Емкость измеряется в фарадах (1Ф).
1Ф – это емкость конденсатора между обкладками которого возникает напряжение 1В при заряде в 1Кл.
В практике встречаются
Индуктивность – это величина, характеризующая способность контура, по которому протекает электрический ток, создавать и накапливать магнитное поле.
Индуктивность измеряется в генри.
1Гн – величина, равная ЭДС самоиндукции, возникающей при изменении величины тока в контуре на 1А в течение 1секунды.
В практике встречаются
Электрическая проводимость – величина, показывающая способность тела проводить электрический ток. Обратная величина сопротивлению.
Что принимается за электрическую постоянную
Фёдоров В.В., Пономарёв Д.А., Бондаренко Т.В.
Прежде чем обсуждать вопрос о роли электрической постоянной в классической электростатике, следует сначала отметить, что в принятой 11-й Генеральной конференцией по мерам и весам (1960) международной системе физических единиц (СИ) среди основных (базисных) нет Кулона [1] – единицы измерения количества электрических зарядов. Выглядит это по меньшей мере как-то странно, так как кулоновское взаимодействие является одним из двух первичных природных стационарных и установлены носители элементарного заряда (установлена его величина (речь не идёт о достоверности)), а вот уже количество зарядов почему-то стали считать производной физической величиной, привлекая к истолкованию ньютоновскую абстракцию. 1 Кл = 1 А × 1 сек, а “ ампер – сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2∙10 –7 Н на каждый метр длины” [2]. Такое определение количественной меры зарядов (посредством абстракции) – это пример из СИ, который явно подчёркивает её “достоинства”. Тот факт, что время отождествляется с длительностью какого-либо процесса [2]: “ Секунда – единица времени, равная 9102631770 периодов излучения, соответствующего между двумя сверхтонкими уровнями основного состояния атома цезия-133”, и возводится в СИ в ранг базисного понятия – это трагедия теоретического естествознания всей ньютоновской эпохи. С абстрактным временем в классике сформированы многие производные понятия (величины), которым даже придумывают какой-то физический смысл, забывая, что абстракция всегда остаётся абстракцией.
Поскольку закон Кулона записан по аналогии с ошибочного закона всемирного тяготения Ньютона, то электрическая постоянная – это всего лишь подгоночный БЕЗРАЗМЕРНЫЙ коэффициент в законе Кулона, который в КТЕ в принципе не мог иметь ни теоретического обоснования, ни соответствующего экспериментального подтверждения.
Несомненно, для начала сама размерность этой постоянной ( фарада/ метр [1, 2]), пожалуй, уже заявляет о том, что её истолкование требует специального уточнения, так как распределение зарядов по проводнику принципиально отличается от распределения массы в этом однородном проводнике. Можно сказать, что заряд подвижен, а на распределение элементарных зарядов по поверхности проводника оказывает непосредственное влияние даже геометрия его поверхности. Этот экспериментальный факт известен каждому исследователю ещё со школьной скамьи, а учитывать его в классике предлагают понятием электроёмкости. Это с одной стороны, а с другой, в классической электростатике фарада – это единица измерения электроёмкости уединённого проводника в вакууме, потенциал φ которого изменяется на 1 вольт при сообщении ему заряда q в 1 кулон [3, стр. 65]:
1 ф = 1 к/1 в. (1) 
Если в классике потенциал поля точечного заряда q в произвольной точке пространства равен (здесь и далее ε = 1)
где ε 0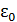 
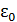
– электрическая постоянная, а r – расстояние (скаляр) от точечного заряда q до точки с пробным единичным зарядом в окружающем пространстве, то в этом случае к величине потенциала, вычисляемой таким образом, пожалуй, сразу возникает возражение: “что конкретного скрывается за безразмерной постоянной ε 0 , когда заряды являются точечными?”. Ответ очевиден и прост – изменение единицы измерения потенциала, и всё. А если заряд q распределён дискретно по поверхности проводника, то?
где k – некоторая функция координат рассматриваемой точки поверхности”.
Несомненно, цитирование классического повествования на этом следовало бы и закончить, так как уже из этого абзаца видно, что при изложении в классике об электроёмкости уединённого проводника используют даже не строгий математический формализм, а набор математических ляпсусов, создавая видимость физико-математического обоснования этому понятию.
Следовательно, k в принципе не может быть функцией координат точки поверхности.
Интегрируя это выражение по всей замкнутой поверхности S заряженного проводника, находим потенциал в произвольной точке его электрического поля:
Заменяя σ по формуле (3) и вынося q за знак интеграла, получаем
2. Из формулы (7) видно, что потенциал уединённого проводника прямо пропорционален его заряду. Отношение q к φ для данного проводника называется электрической ёмкостью (электроёмкостью, или просто ёмкостью) С, т. е.
Авторские возражения на это классическое повествование таковы:
1. Потенциал поля вокруг уединённого точечного заряда – это абстракция, существующая только у теоретиков, которые или не способны осознать, что о характеристике взаимодействия можно говорить только в системе зарядов (не менее двух, разделённых в пространстве), или принципиально не желают устранять очевидные ошибки в теориях (законах) своих предшественников;
где r 0 i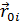 
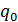
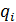
– вектор с началом в пробном точечном заряде q 0 
и концом в точечном одноимённом заряде q i 
.
Совмещая начала декартовой прямоугольной системы координат с единичным точечным зарядом q 0 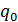, имеем
Если величины q i = q 0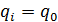 
, то суммарный потенциал в системе “заряженный проводник – пробный заряд в начале координат”, в котором находится пробный заряд, будет определяться следующим выражением:
Различие между классическими определениями (6) и (15) одной и той же характеристики в системе точечных зарядов очевидно, а главное: потенциал – векторная величина. Именно это и должно учитываться при определении потенциала в случае распределения заряда q >> q 0 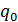по поверхности проводника с произвольной геометрией;
5. Потенциал – векторная величина, а поэтому, руководствуясь только формализмом векторного анализа и принимая во внимание (15), имеем
Здесь очень важно отметить, что три последних выражения формально определяют характеристики электростатического взаимодействия в системе “заряженный проводник – пробный единичный заряд”, причём только (15) и (17) являются векторными, а (16) является скалярной функцией векторного аргумента. (В классике векторную функцию r / r 2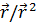 
, где r 
– вектор трёхмерного пространства, ошибочно отождествляют со скалярной функцией 1/ r (где r – расстояние, то есть понятие одномерного пространства), к которой операция дивергенции неприменима по определению!)
Поскольку экспериментально измерять (или компенсировать) можно только интенсивные (векторные) величины, то очевиден вопрос – какой же закон был установлен Кулоном с использованием крутильных весов? Ответ на этот вопрос очевиден и заведомо отрицательный, так как скаляр ( div φ i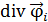 
) не поддаётся экспериментальному определению. Ответ на вопрос об измеряемой величине с использованием крутильных весов при отсутствии обоснованной методики определения величины заряда шара во времена Кулона (да и в настоящее время не блещем достоверностью) вообще следовало считать преждевременным.
Руководствуясь авторским решением проблемы времени, принципом суперпозиции, учитывая симметрию размещения зарядов на сферической поверхности и считая, что точечный заряд q 0 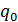(“прибор”) находится в начале системы координат, выражение, определяющее величину ПЕРВОГО векторного электростатического потенциала на поверхности шара, запишем в таком виде:
Подчеркнём, что в определении величины первого потенциала (18) нет места электрической постоянной, как и должно быть. Этим и подчёркивается её надуманная роль в классической электростатике. Это с одной стороны, а с другой, результат (18) соответствует примеру наипростейшей поверхности и возможности сведения задачи по определению величины первого векторного потенциала n одинаковых точечных зарядов, размещённых на поверхности шара, к задаче двух точечных зарядов одинаковой величины, но с иной величиной его радиуса, то есть R = r /( n – 1). Если проводящее тело не является шаром, а представляет собой тело со сложной поверхностью, то задача теоретического определения величины первого векторного потенциала сразу становится практически неразрешимой.
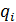
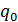
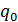
Действительно, для заряженного тела со сложной поверхностью и с неизвестным распределением точечных зарядов ( q i = q 0 ) по поверхности проводника первый потенциал на поверхности его в произвольной точке P(0, 0, 0), в которой и находится заряд q 0 , определяем следующим функциональным выражением:
где i = 1, 2, 3, …, ( n – 1).
Руководствуясь классическим определением электроёмкости тел (8) (вообще-то без зарядов и электростатического взаимодействия) и используя (19), имеем
C = Q φ = 2 n q 0 q i + q 0 ( x i n x + y i n y + z i n z ) = 
Если классическое физико-математическое обоснование понятия электроёмкости в классике (9) – недоразумение, то (20) уже по физическому истолкованию отличается от классического, так как определение величины первого векторного потенциала в авторской электростатике отличается от общепризнанного. Но и это, на взгляд авторов, ещё не решение проблемы электроёмкости в науке. Можно сказать, что никто до сих пор из корифеев классической физики и их единомышленников не замечал отсутствия всестороннего физико-математического обоснования понятия электроёмкости уединённого проводника, а поэтому этот факт уже однозначно заявляет о замшелости всей теоретической электростатики. Творцы классической физики в решении этой проблемы (как и во многих других) плетутся за экспериментаторами, безнадёжно отставая, пожалуй, минимум на столетие.
Это во-первых, а во-вторых, точечные заряды, распределённые по поверхности, например, проводящего уединённого шара находятся в покое относительно друг друга, а поэтому, на взгляд авторов, использование математического аппарата векторного анализа (теории поля) вряд ли приведёт к результату, способному коренным образом изменить ошибочное классическое определение величины электроёмкости рассматриваемого тела.
Из (24) очевидно, что величины понятий поверхностной плотности заряда на шаре и квадрата электростатического потенциала на его поверхности принципиально отличаются друг от друга, то есть
Здесь очень важно подчеркнуть, что только при n = 2 σ > φ 2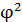 
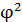
(исключение), а при всех n > 2 σ φ 2 . Поскольку равенство исключено, то все классические рассуждения о возможности использования понятия поверхностной плотности заряда при определении электроёмкости уединённого шара автоматически превращаются, образно выражаясь, в мыльные пузыри.
Несомненно, если электроёмкость проводника является количественной мерой его способности удерживать электрический заряд на своей поверхности [1], то это значит, что величина электроёмкости, например, уединённого шара определяется отношением Q к φ 2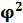 
.
Действительно, если из (22) следует
то величина электроёмкости уединённого шара
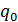
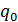
где n – количество элементарных зарядов q 0 на поверхности шара, Q = n q 0 , а r – величина радиуса шара.
Поскольку в классике ёмкость уединённого шара радиуса r [3, стр. 65]
где ε 0 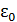= 8,85∙10 –12 ф / м, а r – величина радиуса шара, то возможно сравнение с авторским определением (27) для того же шара в виде отношения, то есть
Подчеркнём, если авторское определение электроёмкости уединённого шара (27) и результат (29) не требуют каких-либо дополнительных пояснений, то утверждение, отражающее классические взгляды на понятие электроёмкости [3, стр. 65]: “ Ни от материала проводника, ни от его агрегатного состояния, ни от формы и размеров возможных полостей внутри проводника его электроёмкость не зависит. Это связано с тем, что избыточные заряды распределены только на внешней поверхности проводника. Следует заметить, что С также не зависит ни от заряда проводника, ни от его потенциала. Это совершенно не противоречит соотношению (8), которое лишь показывает, что потенциал уединённого проводника прямо пропорционален его заряду и обратно пропорционален ёмкости”, – требует принципиальных изменений и они таковы:
Итак, электрическая постоянная с размерностью в классике фарад на метр [1] – безразмерная величина, которая только по недоразумению в классической физике отнесена к перечню фундаментальных физических постоянных. Её роль в теоретической электростатике заведомо негативна, а появление её связано всего лишь с записью закона электростатического взаимодействия зарядов по образу и подобию закону всемирного тяготения Ньютона.
Закон Кулона – это умозаключение по аналогии с ошибочного закона Ньютона, для которого теоретическое обоснование методики эксперимента вообще не рассматривалось одним из решающих критериев для проверки достоверности гипотезы. Аналогия вообще не является доказательством, а если ещё исходный “закон” ошибочен, то и его аналог от него не может отличаться. Цена такой аналогии зависит от роли исходного и его аналога в теоретическом естествознании. В данном случае речь идёт не о каких-то второстепенных законах физики, а о фундаментальных законах первичных природных взаимодействий, которые своей достоверностью олицетворяют путь развития всего теоретического естествознания. Опираясь только на аналогию, Кулон повторил ошибку Ньютона. В экспериментах с заряженными шарами Кулон в принципе не мог получить даже результатов, позволяющих сформулировать гипотезу о взаимодействии зарядов, поскольку величину заряда шаров он мог делить только пополам, но не определять её количественно. Заметим, между шарами существует ещё и гравитационное взаимодействие, которое необходимо учитывать, причём руководствуясь не ошибочным законом Ньютона.
Не будет излишним обратить внимание теоретиков естествознания на то, что Международная система единиц измерения (СИ) является, пожалуй, одним из последних документов, в котором мировое научное сообщество ещё пытается оградить от конструктивной критики бесплодное наследие Ньютона в теоретическом естествознании. Это подтверждается тем, что в перечне основных (базисных) единиц измерения сохранено абстрактное время ( ньютоновская длительность), а базисное понятие заряда (количество элементарных зарядов) включено в перечень производных единиц измерения. Этого уже вполне достаточно для того чтобы признать, что создание СИ вообще вряд ли способствует фактическому прогрессу теоретического естествознания, а лишь имитирует его. В такой системе единиц физических величин теоретическое естествознание (физика реальных тел) не нуждается, а утверждение [1]: “ Первые три основные единицы ( метр, килограмм, секунда) позволяют образовывать согласованные производные единицы для всех величин, имеющих механическую природу”, – лишь автоматически повторяет ошибки своих предшественников. Вряд ли имеет смысл в теоретическом естествознании заниматься согласованием между собой производных единиц, если они сформированы с использованием абстрактного базиса! К базисным понятиям в теоретическом естествознании относятся масса, заряд и расстояние, а производные для соответствующих разделов физики реальных тел (частиц) формируются с использованием этого перечня или его части.
Несомненно, что до тех пор пока в теоретическом естествознании время будут считать базисным понятием, а не производной физической величиной, такое естествознание было и будет спекулятивным. С использованием “ впечатления” (Лаплас о времени) производных единиц измерений не формируют и физических теорий не разрабатывают.
1. Физический энциклопедический словарь. М., “Советская энциклопедия”, 1983.
2. Яворский Б.М. и Детлаф А.А., Справочник по физике. М., Наука, Главная редакция физико-математической литературы, 1981.
3. Яворский Б.М., Детлаф А.А., Милковская Л. Б., Курс физики, том 2. М., изд-во “Высшая школа”, 1966.
С уважением, авторы.
С реакцией на данное сообщение можно познакомиться на следующих научных форумах: