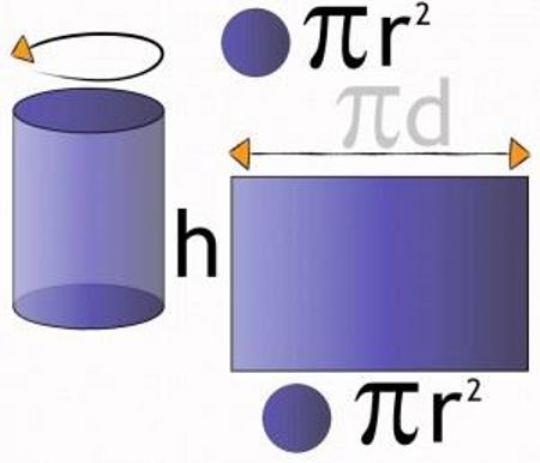
Что принимается за площадь боковой поверхности цилиндра

Нахождение площади поверхности цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.

Формула вычисления площади цилиндра

1. Боковая поверхность

Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.

Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:

S = 2 π R h

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:

S = π R 2

Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:

3. Полная площадь

Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:

S = 2 π R h + 2 π R 2 или S = 2 π R (h + R)

Примеры задач

Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.

Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.

Источник

Площадь поверхности цилиндра – формула полной и боковой площади поверхности

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь цилиндра и, применив формулу, решим для примера несколько задач.

У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

Вершина и основание цилиндра являются окружностями, их легко определить.

Известно, что площадь окружности равна πr2. Поэтому, формула площади двух окружностей (вершины и основания цилиндра) будет иметь вид πr2 + πr2 = 2πr2.

Боковая поверхность цилиндра

Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Вершина исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Формула площади боковой поверхности цилиндра
Sбок. = 2πrh
r – радиус цилиндра, h – высота цилиндра

Площадь полной поверхности цилиндра

Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площади поверхности цилиндра равна площадь вершины цилиндра + площадь основания цилиндра + площадь боковой поверхности цилиндра или S = πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).

Формула площади полной поверхности цилиндра
S = 2πr2 + 2πrh = 2πr(r + h)
r – радиус цилиндра, h – высота цилиндра

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

Площадь полной поверхности рассчитывается по формуле: Sбок. = 2πrh

Sбок. = 2 * 3,14 * 2 * 3

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

Площадь полной поверхности рассчитывается по формуле: S = 2πr2 + 2πrh

S = 2 * 3,14 * 62 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

Источник

Площадь поверхности цилиндра

Всего получено оценок: 9335.

Всего получено оценок: 9335.

Цилиндр представляет собой геометрическое тело, ограниченное двумя параллельными плоскостями и цилиндрической поверхностью. В статье поговорим о том, как найти площадь поверхности цилиндра и, применив формулу, решим для примера несколько задач.

У цилиндра есть три поверхности: вершина, основание, и боковая поверхность.

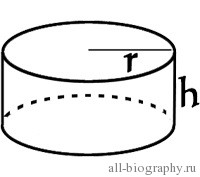
Основаниями цилиндра (их два: верхние и нижнее) являются окружности, их легко определить.

Боковая поверхность цилиндра

Третья, боковая поверхность цилиндра, является изогнутой стенкой цилиндра. Для того чтобы лучше представить эту поверхность попробуем преобразовать её, чтобы получить узнаваемую форму. Представьте себе, что цилиндр, это обычная консервная банка, у которой нет верхней крышки и дна. Сделаем вертикальный надрез на боковой стенке от вершины до основания банки (Шаг 1 на рисунке) и попробуем максимально раскрыть (выпрямить) полученную фигуру (Шаг 2).

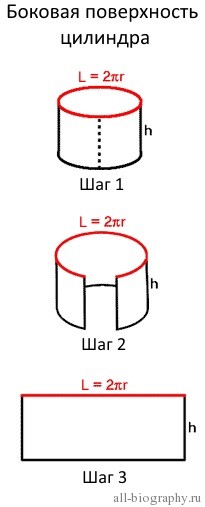
После полного раскрытия полученной банки мы увидим уже знакомую фигуру (Шаг 3), это прямоугольник. Площадь прямоугольника вычислить легко. Но перед этим вернемся на мгновение к первоначальному цилиндру. Верхнее основание исходного цилиндра является окружностью, а мы знаем, что длина окружности вычисляется по формуле: L = 2πr. На рисунке она отмечена красным цветом.

Когда боковая стенка цилиндра полностью раскрыта, мы видим, что длина окружности становится длиной полученного прямоугольника. Сторонами этого прямоугольника будут длина окружности(L = 2πr) и высота цилиндра(h). Площадь прямоугольника равна произведению его сторон – S = длина х ширина = L x h = 2πr x h = 2πrh. В результате мы получили формулу для расчета площади боковой поверхности цилиндра.

Площадь полной поверхности цилиндра

Наконец, если мы сложим площадь всех трёх поверхностей, мы получим формулу площади полной поверхности цилиндра. Площадь полной поверхности цилиндра равна площадь верхнего основания цилиндра + площадь нижнего основания цилиндра + площадь боковой поверхности цилиндра или S = πr 2 + πr 2 + 2πrh = 2πr 2 + 2πrh. Иногда это выражение записывается идентичной формулой 2πr (r + h).

Примеры расчета площади поверхности цилиндра

Для понимания приведенных формул, попробуем посчитать площадь поверхности цилиндра на примерах.

1. Радиус ос­но­ва­ния цилиндра равен 2, высота равна 3. Определите площадь боковой поверхности цилиндра.

S_бок. = 2 * 3,14 * 2 * 3

Площадь боковой поверхности цилиндра равна 37,68.

2. Как найти площадь поверхности цилиндра, если высота равна 4, а радиус 6?

S = 2 * 3,14 * 6 2 + 2 * 3,14 * 6 * 4

S = 2 * 3,14 * 36 + 2 * 3,14 * 24

Площадь поверхности цилиндра равна 376,8.

3. Площадь боковой поверхности прямого кругового цилиндра равна 24π, а диаметр основания — 3. Найдите высоту цилиндра.

Из формулы расчета площади боковой поверхности цилиндра Sбок. = 2πrh следует, что высота равна:

Значение радиуса получаем из формулы: d = 2r

Источник

Цилиндр: площадь боковой поверхности. Формула площади боковой поверхности цилиндра

При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.

Понятие цилиндра

Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.

Вам будет интересно: Возможность оценить себя, или Что значит потупить взгляд

Существуют разновидности данной объемной фигуры:

Условные обозначения

Традиционно основные «компоненты» цилиндра принято называть следующим образом:

«Компоненты» стереометрической фигуры

Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.

Основными составляющими фигуры являются:

Основные формулы для работы с цилиндром

Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.

Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем – для прямого.

Примеры с разобранным решением

Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается

Решение. Поскольку известны величины диагонали и угла, то в таком случае:

Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.

Аналогично, можно найти и значение AD:

Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.

Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?

Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.

Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.

Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.

Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.

Ответ: Smin будет достигнута при h = 1/32 см, R = 64 см.

Дана стереометрическая фигура – цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.

Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.

Отсюда можно сделать вывод, что МК = ВС = 8 см.

Следующий шаг – проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.

AD – диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.

BC – прямая, расположенная на плоскости имеющегося прямоугольника.

ABCD – трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.

Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.

Для этого необходимо найти величины AD и ОС.

Ответ: сечение располагается 3 см от оси.

Задачи на закрепление материала

Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания – Q, площадь осевого сечения – М. Необходимо найти S. Иными словами, полную площадь цилиндра.

Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.

Источник

Урок на тему: «Площадь боковой поверхности цилиндра»

Тема урока: Площадь боковой поверхности цилиндра.

образовательная: сформировать системность знаний учащихся по теме «Цилиндр. Площадь поверхности цилиндра»; включить знания и способы действий учащихся по данной теме в уже имеющуюся у них систему знаний и способов действий; выявить уровень усвоения знаний учащихся по данной теме;

развивающая: развитие умений использовать знания, умения и навыки в учебной деятельности; развитие логического мышления (на основе усвоения учащимися причинно-следственных связей, сравнительного анализа), способности четко формулировать свои мысли; совершенствование навыков письменной и устной речи;

воспитательная: воспитывать у учащихся средствами урока уверенность в своих силах, уважительное отношение к своим товарищам, аккуратность, инициативность.

Оборудование урока: набор геометрических тел, тест.

Этап актуализации субъективного опыта учащихся

Дать определение цилиндра

Укажите в природе, технике, архитектуре, среди окружающих вас предметов объекты, имеющие цилиндрическую форму

Дать определение боковой поверхности цилиндра

4) Назовите основные элементы цилиндра, дайте им определение

5) Что такое осевое сечение цилиндра? Что представляет собой осевое сечение цилиндра?

6) Может ли осевое сечение цилиндра быть (ответ обоснуйте): а) трапецией; б) квадратом?

7) Радиус основания цилиндра 2м, высота 3м. Найдите диагональ осевого сечения.

8) Что такое поперечное сечение цилиндра? Что представляет собой такое сечение?

9) Вычислите площадь сечения цилиндра, если радиус его основания равен 5см

10) Что представляет собой развертка цилиндра?

Этап изучения новых знаний и способов деятельности (параллельно проходит этап первичной проверки понимания изученного материала)

а) Задача (проблемная ситуация)

Из куска ткани необходимо сшить головной убор для повара. Хватит ли нам для изготовления изделия куска прямоугольной формы, если его длина 80см, а ширина – 30см (размер головы – 54, а высота изделия – 25см)?

б) Уч-ся самостоятельно изучают по плану материал учебника.

Площадь боковой поверхности цилиндра

Формула для вычисления площади боковой поверхности цилиндра

Площадь полной поверхности цилиндра

Формула для вычисления площади полной поверхности цилиндра

Этап первичного понимания изученного

Учащиеся отвечают на вопросы учителя:

а) Что принимается за площадь боковой поверхности цилиндра?

— За площадь боковой поверхности цилиндра принимается площадь её боковой развертки

б) Формула для вычисления площади боковой поверхности цилиндра

в) Что принимается за площадь полной поверхности цилиндра?

— Площадь полной поверхности цилиндра равна сумме площадей боковой поверхности и двух оснований

г) Формула для вычисления площади полной поверхности цилиндра.

Итак, на нашем уроке основными формулами являются формулы для вычисления площади боковой и полной поверхности цилиндра

Этап закрепления изученного

У доски № Выполнение теста.

Этап обобщения и систематизации

Этап информации о Д/З №

Этап подведения итогов учебного занятия

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1690711

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

В Липецкой области начинающие педагоги получат 120 тысяч рублей

Время чтения: 0 минут

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Рособрнадзор не намерен упрощать ЕГЭ в 2022 году из-за пандемии

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Думу внесли законопроект об обязательном образовании для находящихся в СИЗО подростков

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник