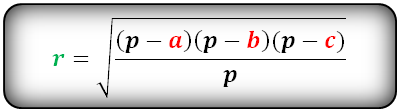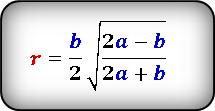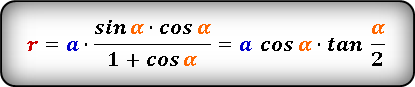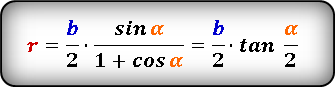Как вписать круги в круг
Круги в круге
Задача
Чему равен наименьший радиус круга, в котором можно разместить без наложений 7 единичных кругов? Обоснуйте ваш ответ.
Примечание. Единичный круг — круг радиуса 1. «Без наложений» означает, что круги могут касаться, но не должны иметь общих внутренних точек.
Подсказка 1
Радиус равен 3, а «оптимальная картинка» выглядит именно так, как вы ее себе, скорее всего, и представили (рис. 1).
Подсказка 2
Удобно избавиться от понятия «наложение», перейдя от этой задачи к такой:
Рассмотрим вместо кругов только их центры. В круг какого наименьшего радиуса можно их все уместить?
В «оптимальной картинке» все центры являются вершинами и центром правильного шестиугольника со стороной 2 (рис. 2). При этом расстояние между любыми двумя вершинами и центром такого шестиугольника тоже равно 2, поэтому все точки лежат в круге радиуса 2. Нужно обосновать, что все эти точки нельзя уместить в круг меньшего радиуса. Для этого попробуйте рассмотреть случаи, сколько именно (из шести отличных от центра) точек образуют выпуклый многоугольник.
Решение
Будем действовать методом «от противного». Предположим, что шесть точек с попарным расстоянием 2 (или большим двух), удалось поместить в круг радиуса R BA и CH > CA. То есть при сдвиге A в H расстояния до точек B и C увеличились.
Наконец, если все точки лежат на единичной окружности, то они делят ее на 6 дуг, поэтому длина наименьшей из дуг не больше, чем 1/6 длины окружности, то есть не больше 2π/6. Это значит, что величина центрального угла этой дуги также не превышает 2π/6, а значит, расстояние между двумя точками, являющимися концами этой дуги, не больше 2sin(π/6) = 1.
Послесловие
Эта задача является примером огромного класса так называемых «минимаксных» задач вычислительной геометрии. В минимаксных задачах ищется наибольшее возможное значение какой-то величины, которая сама определена как наименьшее значение другой величины. В нашем случае минимаксная задача (к которой мы свели исходную) была такой: сначала среди всех 15 попарных расстояний между шестью точками в единичном круге выбирается наименьшее, а затем ищется такая конфигурация шести точек, для которой это расстояние будет максимальным из возможных.
Приведенное нами утверждение и его доказательство принадлежат замечательному американскому математику Рональду Грэхему (Ronald Graham), они опубликованы в 1968 году. Грэхем доказал даже более общую оценку для наименьшего расстояния d между какими-то из k точек, лежащих в единичном круге. Эта оценка имеет вид
(то есть d не превышает наибольшего из двух чисел — единицы и удвоенного синуса). Оценка Грэхема является оптимальной для 2 ≤ k ≤ 7, то есть существуют картинки, для которых достигаются значения из правой части этого неравенства. Для больших значений k указанная оценка неточна, поскольку она дает d ≤ 1, а на самом деле наибольшее из возможных значений минимального расстояния между точками строго меньше 1.
Естественное обобщение нашей задачи — поиск кругов наименьшего радиуса, в которые можно поместить N единичных кругов (или, что то же самое, поиск решения минимаксной задачи об N точках в единичном круге). В этом поиске усилия математиков сконцентрировались на двух направлениях — компьютерном моделировании и доказательствах оптимальности. Ниже на рис. 5 показаны несколько очевидных оптимальных картинок.
Оптимальность первых трех из них следует из приведенного выше результата Р. Грэхема. Оптимальность последней (для 8 кругов) была доказана в 1963 году голландцем Boele L. J. Braaksma в его диссертации под труднопроизносимым названием «Асимптотические расширения и аналитические продолжения для одного класса интегралов Барнса». Следующее продвижение, а также оптимальность вот такой вот картинки (рис. 6) с двумя внутренними кругами (для 10 кругов)
было получено немцем U. Pirl в 1969 году. Оптимальность аналогичной картинки для 11 кругов доказана еще на 25 лет позже, а для 12, 13 и 19 кругов — еще позже (последний из результатов — в 2003 году).
И. всё. Остальные результаты об упаковке кругов в круг на сегодняшний день находятся в состоянии «оптимальность предполагается, но не доказана». Так что просто полюбуйтесь на картинки (рис. 7) с доказанной оптимальностью (N = 12 и N = 19) и оцените: всего каких-то 15 лет назад это была терра инкогнита, обе задачи еще ждали своего решателя.
А следующие две картинки (для N = 14 и N = 15 соответственно) являются этой самой «инкогнитой» и сейчас (рис. 8). Дерзайте.
См. также:
1) Circle packing in a circle («Упаковка кругов в круг»). Достаточно детальная статья английской Википедии.
2) Circles in Circles. Страничка Эрика Фридмана, откуда мы позаимствовали большую часть иллюстраций. Там же на соседних страницах packing center рассказано о других задачах упаковки.
3) K. A. Dowsland, M. Gilbert, G. Kendall. A local search approach to a circle cutting problem arising in the motor cycle industry (PDF, 346 Кб). Статья в научном журнале Operational Research Society — международного сообщества, занимающегося исследованием операций, то есть научной дисциплиной, чья основная задача — обоснование оптимальности применения каких-либо научных достижений на практике.
В статье объясняется, как можно оптимизировать изготовление «звездочек» и других профилированных колёс (для зубчатых передач и др.) при производстве велосипедов и мотоциклов. С точки зрения математики — абсолютно ничего нового, но связь с практикой очень забавна. Интересно, появится ли когда-нибудь подобная статья для домохозяек — об оптимизации раскладывания котлет на сковородке?
Вписанная окружность
Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.
Окружность, точно можно вписать в такие геометрические фигуры, как:
В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.
Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.
Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.
Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.
Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.
Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.
Свойства вписанной окружности
В треугольник
\[ S = \frac<1><2>(a+b+c) \cdot r = pr \]
с — расстояние между центрами вписанной и описанной окружностей треугольника.
R — радиус описанной около треугольника.
r — радиус вписанной окружности треугольника.
В четырехугольник
\[ S = \frac<1><2>(a+b+c+d)\cdot r = pr \]
Примеры вписанной окружности
Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.
Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.
Верные и неверные утверждения
Окружность вписанная в угол
Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.
Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.
К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.
Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.
Вписанная окружность (ЕГЭ 2022)
Ну что, юнга, уверен, что знаешь все про окружности?
Пров вписанную точно знаешь. А про вневписанную слышал?
Ничего страшного, сейчас ты во всём разберешься!
Вписанная окружность — коротко о главном
Вписанная в треугольник окружность — окружность, которая касается всех (трёх) сторон треугольника.
В любой треугольник можно вписать окружность, причём единственным образом.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Отрезки от вершин треугольника до точек касания выражаются по формулам:
Площадь треугольника через радиус вписанной окружности:
\( \displaystyle S=p\cdot r\), где \( \displaystyle p=\frac
Вневписанная окружность – окружность, которая касается одной стороны треугольника и продолжений двух других сторон.
Центр вневписанной окружности лежит на пересечении биссектрисы внутреннего угла треугольника (\( \displaystyle \angle A\)) и биссектрис двух внешних углов (\( \displaystyle \angle B\) и \( \displaystyle \angle C\)).
Площадь треугольника через радиус вневписанной окружности:
\( \displaystyle <_<\Delta ABC>>=(p-a)\cdot r\), где \( \displaystyle p=\frac
Вписанная окружность — подробнее
Здесь мы будем говорить об окружностях, связанных с треугольником. Оставим пока в стороне страшное слово «вневписанная» и поговорим об окружности, вписанной в треугольник.
Итак, что же это такое?
Окружность называется вписанной в треугольник, если она касается всех(трёх) его сторон.
Для всякого ли треугольника можно подобрать такую окружность? И как найти ее центр?
На эти вопросы отвечает следующая теорема:
Во всякий треугольник можно вписать окружность, причём единственным образом.
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
И повторим ещё раз то, что очень нужно запомнить:
Центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Если тебя заинтересовал вопрос о том, почему это все три биссектрисы обязаны пересечься, и какое отношение имеют биссектрисы к тому, что окружность касается сторон треугольника, то добро пожаловать к теме «Биссектриса».
Но для начала хватит просто запомнить то, что центр вписанной окружности лежит на пересечении биссектрис углов треугольника.
Теперь немножко о радиусе.
Радиус вписанной окружности
Посмотри, пусть у нас в \( \displaystyle \Delta ABC\) вписана окружность с центром \( \displaystyle O\).
Тогда отрезки \( \displaystyle OK\), \( \displaystyle OL\), и \( \displaystyle OM\) – радиусы этой окружности.
Поэтому они, конечно же, равны, но ещё – они все перпендикулярны сторонам. Это происходит оттого, что радиус, проведенный в точку касания, перпендикулярен касательной.
Итак, запомни и используй:
Вписанная окружность и отрезки сторон треугольника
Давай представим, что мы откуда-то узнали все три стороны треугольника.
Можно ли найти как-то отрезочки \( \displaystyle AK\), \( \displaystyle KC\), \( \displaystyle BL\) и.д. —отрезки, на которые точки касания разбивают стороны треугольника?
Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).
Посмотри внимательно: из точки \( \displaystyle A\) проведено две касательных, значит их отрезки \( \displaystyle AK\) и \( \displaystyle AM\) равны.
Мы обозначим их «\( \displaystyle x\)».
Далее, точно так же:
\( \displaystyle BM=BL=y\) (обозначили).
\( \displaystyle CK=CL=z\) (обозначили).
Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины «\( \displaystyle a\)», «\( \displaystyle b\)», «\( \displaystyle c\)» — смотри на рисунок. Что же теперь получилось?
А вот, например, отрезок «\( \displaystyle a\)» состоит из двух отрезков «\( \displaystyle y\)» и «\( \displaystyle z\)», да и отрезки «\( \displaystyle b\)» и «\( \displaystyle c\)» тоже из чего-то состоят. Запишем это всё сразу:
Ух ты! Выход в алгебру! Три уравнения и три неизвестных! Сейчас решим!
Сложим первые два уравнения и вычтем третье:
\( \displaystyle \left\< \begin
А теперь сложим первое и третье уравнение и вычтем второе:
\( \displaystyle \left\< \begin
И последний шаг: сложим второе и третье, а потом вычтем первое.
Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.
Секрет вот в чём: те стороны, на которых есть «\( \displaystyle x\)» («\( \displaystyle b\)» и «\( \displaystyle c\)») будут с плюсом, а та сторона, где нет «\( \displaystyle x\)» (это «\( \displaystyle a\)»), будет с минусом.
Ну, а пополам поделить всё хозяйство. С другими буквами точно так же
На «\( \displaystyle a\)» и «\( \displaystyle c\)» есть «\( \displaystyle y\)» — они с плюсом, на «\( \displaystyle b\)» нет «\( \displaystyle y\)» — она с минусом
На «\( \displaystyle a\)» и «\( \displaystyle b\)» есть «\( \displaystyle z\)» — они с плюсом, на «\( \displaystyle c\)» нет «\( \displaystyle z\)» — она с минусом.
Вписанная окружность и площадь
Здесь скажем совсем коротко:
Есть такая формула:
\( \huge\displaystyle S=p\cdot r\),
где \( \displaystyle p\) — это полупериметр треугольника, то есть \( \displaystyle p=\frac
Вневписанная окружность
Ну вот, пора приступать к самому непонятному. Что же это за зверь такой: «вневписанная окружность»? Сначала посмотри на картинку:
Видишь, окружность тоже чего-то касается, но «сидит» как-то снаружи, вне треугольника? Вот поэтому и называется вневписанной.
Окружность называется вневписанной для треугольника, если она касается ОДНОЙ стороны треугольника и продолжений двух других сторон.
А как ты думаешь, сколько у одного треугольника может быть вневписанных окружностей? Вот, представь себе, аж три!
Захватывает дух? Насладись впечатлением.
А еще подумай над тем…
А сейчас вернёмся к одной какой-нибудь вневписанной окружности и узнаем всего один, но очень важный факт:
До дальней точки касания вневписанной окружности ровно полупериметр
или что то же самое: \( \displaystyle AK=AM=p\), где \( \displaystyle p\) — полупериметр.
Доказывать не будем, но ещё раз посмотри и запомни:
До «дальней» точки касания вневписанной окружности – ровно полупериметр треугольника.
Наши курсы по подготовке к ЕГЭ по математике, информатике и физике
Курсы для тех, кому нужно получить 90+ и поступить в топовый ВУЗ страны.
Слово лучшему ученику — тебе! 🙂
Навыки работы с окружностями показывают, насколько ты хорош в планиметрии. Это действительно сложная тема.
А сегодня ты с ней разобрался. Ты большой молодец!
Мы будем очень рады узнать твое мнение об этой статье. Для нас оно очень важно.
Напиши внизу в комментариях, что думаешь об этой статье. Помогла ли она тебе?
Нравится ли тебе работать с окружностями? И стало ли это делать легче после прочтения этой статьи? 🙂
Остались вопросы? Задай их! Там же, в комментариях.
Мы обязательно ответим тебе!
Добавить комментарий Отменить ответ
Один комментарий
Некоторые комментарии прошлых лет к этой статье:
Андрей
11 июля 2018
Прекрасное обьяснение, спасибо большое!
Александр (админ)
12 июля 2018
И тебе спасибо, Андрей. За теплые слова.
Юлия
09 сентября 2018
все просто и понятно, спасибо большое!
Александр (админ)
09 сентября 2018
И тебе спасибо, Юлия! Очень приятно слышать!
Миша
28 сентября 2018
не подскажите, почему отрезок о3б перпендикулярен отрезку о1о2?
Александр
21 августа 2019
Это биссектрисы смежных углов.
Денис
24 февраля 2019
Божественные рисунки!) Мне в школе для урока по геометрии надо подготовить несколько рисунков. Подскажите, пожалуйста, какой программой вы пользуетесь для построения рисунков?
Александр (админ)
07 марта 2019
Денис, прошу прощения, пост твой пропустил. Только сейчас отвечаю. Но врядли чем-то помогу. Рисунки делались так: сначала их от руки делала Елена Евгеньевна (наш математик), а потом профессиональный дизайнер Настя их перерисовывала. По-моему в фотошопе.
Все формулы для радиуса вписанной окружности
Радиус вписанной окружности в треугольник
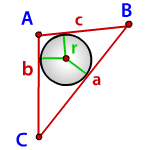
Формула радиуса вписанной окружности в треугольник ( r ):
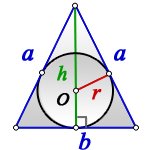
Радиус вписанной окружности в равносторонний треугольник
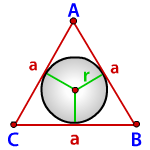
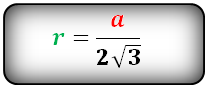
Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):
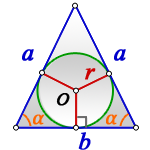
Радиус вписанной окружности равнобедренный треугольник
1. Формулы радиуса вписанной окружности если известны: стороны и угол
Формула радиуса вписанной окружности в равнобедренный треугольник через стороны ( r ) :
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол ( r ) :
2. Формулы радиуса вписанной окружности если известны: сторона и высота
Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту ( r ) :
Как вписать круги в круг
Ключевые слова: окружность, описанная окружность, центр окружности, вписанная окружность, треугольник, четырехугольник, вневписанная окружность
Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.
Окружность называется вписанной в выпуклый многоугольник, если она лежит внутри данного многоугольника и касается всех прямых, проходящих через его стороны.
Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.
Сам многоугольник в таком случае называется описанным около данной окружности.
Таким образом, в выпуклый многоугольник можно вписать не более одной окружности.
Для произвольного многоугольника невозможно вписать в него и описать около него окружность.
Для треуголь ника это всегда возможно.
Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а её центр находится внутри окружности
Серединным перпендикуляром называют прямую перпендикулярную отрезку и проходящую через его середину.
Окружность называется описанной около треугольника, если она проходит через три его вершины.
Окружность, вписанная в прямоугольный треугольник
Окружность, описанная около прямоугольного треугольника
Четырехугольник, вписанный в окружность
Окружность, вписанная в ромб