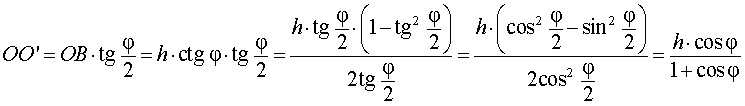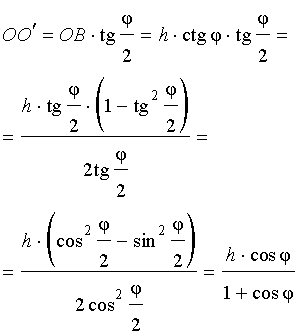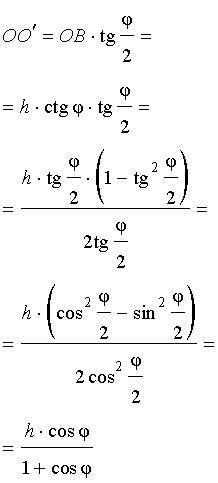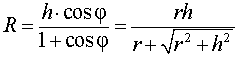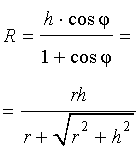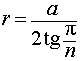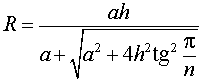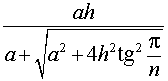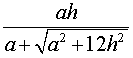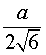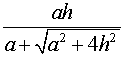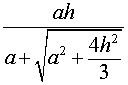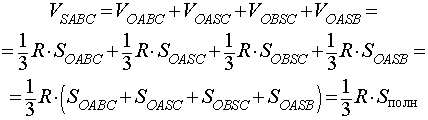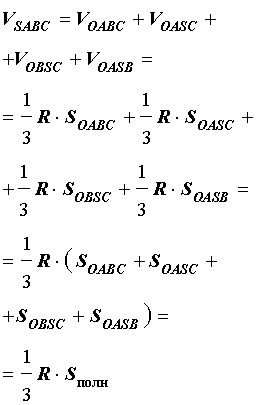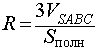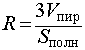Как вписать сферу в тетраэдр

Сфера, вписанная в многогранник

Определение. Сфера называется вписанной в многогранник, если плоскости всех граней многогранника касаются сферы в тачках, расположенных внутри этих граней. При этом многогранник называется описанным около сферы.

Теорема 1.В произвольный тетраэдр можно вписать сферу (шар).

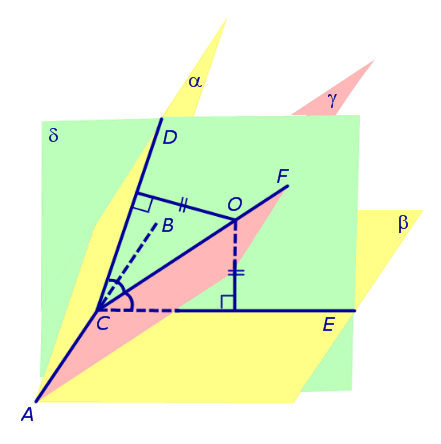
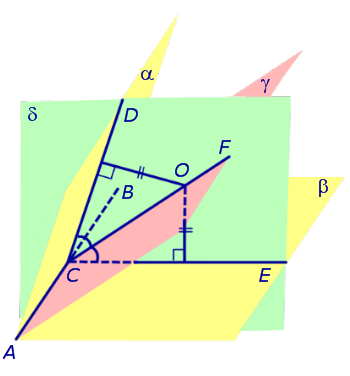
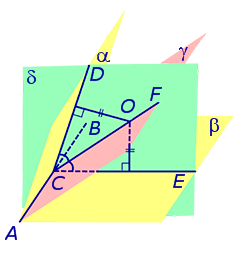
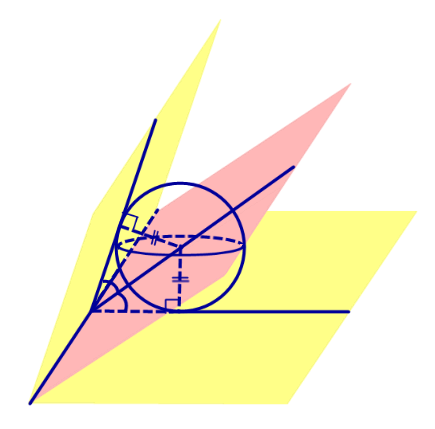
Множество точек, равноудаленных от боковых граней тетраэдра есть прямая пересечения двух биссекторных плоскостей двугранных углов при двух боковых ребрах. Эту прямую пересечет биссекторная плоскость двугранного угла при основании. Полученная точка равноудалена от всех граней тетраэдра.

В тетраэдре ABCD плоскости CDN и ADM являются биссекторными плоскостями двугранных углов при боковых ребрах CD и AD. Они пересекаются по прямой OD. Плоскость AKC является бисссекторной плоскостью двугранного угла при основании (ребро AC). Эта плоскость пересечет прямую OD в точке S (P – точка пересечения прямых DM и KC, принадлежащая плоскостям AKC и ADM одновременно, следовательно точка S – точка пересечения AP и OD), которая будет являться точкой, равноудаленной от всех граней тетраэдра и, следовательно, будет являться центром сферы, вписанной в тетраэдр ABCD.

Пример 1. Найти радиус сферы, вписанной в правильный тетраэдр.

Рассмотрим подобные треугольники DPS и DOK (по двум углам: угол D – общий, углы DPS и DOK – прямые).

если учесть, что PS=r=SO и DS=DO-SO=DO-r,

, , то .

Ответ: радиус сферы, вписанной в правильный тетраэдр равен

Теорема 2. В правильную пирамиду можно вписать сферу.

Теорема 3. В правильную усеченную пирамиду можно вписать сферу тогда и только тогда, когда ее апофема равна сумме радиусов окружностей, вписанных в ее основания.

Теорема 4. В любую призму можно вписать сферу, если в ее перпендикулярное сечение можно вписать окружность, радиус которой равен половине высоты призмы.

Теорема 5. В правильную призму можно вписать сферу тогда и только тогда, когда высота призмы равна диаметру окружности, вписанной в ее основание.

Сферы, описанные около цилиндра, конуса и

Усеченного конуса.

Определение. Сфера называется описанной около цилиндра или усеченного конуса, если все точки окружностей оснований принадлежат сфере; Сфера называется описанной около конуса, если все точки окружности основания, а также вершина конуса принадлежат сфере.

В этих случаях говорят, что цилиндр, усеченный конус или конус вписан в сферу.

Теорема 1.Около произвольного цилиндра можно описать сферу.

О₁ и О₂ – центры нижнего и верхнего основания соответственно. Прямая О₁О₂ перпендикулярна плоскостям основания. Проведем плоскость, проходящую через середину образующей цилиндра, перпендикулярно этой образующей. Эта плоскость будет параллельна плоскостям основания и пересекать прямую О₁О₂ в точке О, которая и будет являться центром сферы, описанной около цилиндра. Расстояние от точки О до всех точек основания будет равным, так как О₁О₂ является ГМТ, равноудаленных от окружности (прямая, проходящая через центр окружности и перпендикулярна плоскости окружности). Значит точка О является центром сферы с радиусом ОА, описанной около цилиндра.

Теорема 2. Около усеченного конуса можно описать сферу.

О₁ и О₂ – центры нижнего и верхнего основания соответственно. Прямая О₁О₂ перпендикулярна плоскостям основания. Рассмотрим образующую усеченного конуса АВ. Найдем ГМТ, равноудаленных от тачек А и В. Им будет являть плоскость, проходящая через точку Р – середину АВ и перпендикулярная этой прямой. Эта плоскость пересечет О₁О₂ в точке О, которая будет равноудалена от точек А и В. Также очевидно, что точка О будет равноудалена от все точек оснований усеченного конуса. Следовательно эта точка О будет являться центром сферы с радиусом ОА, описанной около усеченного конуса.

Теорема 3. Около конуса можно описать сферу.

Аналогично прошлой теореме ОА – высота конуса, которая является ГМТ, равноудаленных от окружности. Рассмотрим образующую АВ и найдем ГМТ, равноудаленных от А и В. Полученная плоскость (по предыдущей задаче) пересечет ОА в точке О₁, которая будет равноудалена от точек А и В, как и от любых точек основания конуса. Таким образом мы получили, что точка О₁ является центром сферы с радиусом О₁А, описанной около конуса.

Источник

Нахождение радиуса шара (сферы), вписанного в правильную пирамиду

В данной публикации представлены формулы, с помощью которых можно найти радиус шара (сферы), вписанного в правильную пирамиду: треугольную, четырехугольную, шестиугольную и тетраэдр.

Формулы расчета радиуса шара (сферы)

Приведенная ниже информация применима только к правильным пирамидам. Формула для нахождения радиуса зависит от вида фигуры, рассмотрим самые распространенные варианты.

Правильная треугольная пирамида

Если известны значения этих величин, то найти радиус (r) вписанного шара/сферы можно по формуле:

Частный случай правильной треугольной пирамиды – это правильный тетраэдр. Для него формула нахождения радиуса выглядит следующим образом:

Правильная четырехугольная пирамида

Радиус (r) вписанного шара/сферы рассчитывается так:

Правильная шестиугольная пирамида

Радиус (r) вписанного шара/сферы вычисляется по формуле:

Источник

638. Докажите, что: а) около любого тетраэдра можно описать сферу; б) в любой тетраэдр можно вписать сферу.

а) Докажем, что через любые 4 точки, не лежащие в одной плоскости, можно провести сферу и притом только одну. (см.ниже).

Геометрическим местом точек пространства, равноудаленных от концов отрезка, является плоскость, перпендикулярная этому отрезку и проведенная через его середину. Следовательно, центр сферы, описанной около тетраэдра, принадлежит каждой из плоскостей, проведенных через середины ребрер тетраэдра перпендикулярно к этим ребрам.

Пусть О — центр окружности, описанной около грани АВС тетраэдра, d— прямая, которая проходит через точку О, d ⊥ плоскости АВС. Все точки прямой d равноудалены от точек А, В и С. (ОА=ОВ=ОС=r — радиус описанной окружности). Если точка S ∈ d, то прямоугольные треугольники SOA, SOB, SOC равны двум катетам. Следовательно, SA=SB=SC.

Пусть плоскость α проходит через середину ребра DA и плоскость α ⊥ DA. Докажем, что d и α пересекаются. Предположим, что α || d.

Если α ⊥ AD и d ||α, то AD ⊥ d. Кроме того, d ⊥ АВ (поскольку d ⊥ плоскости АВС), и, значит d ⊥ ABD — по признаку перпендикулярности прямой плоскости.

Таким образом, через точку А проведены две различные плоскости АВС и АВD, перпендикулярные к одной прямой, что невозможно. Значит предположение, что d || α неверно.

Значит, пусть точка S точка пересечения d и α. Тогда SD=SA, т.к. S принадлежит каждой плоскости, проходящей через середину ребра тетраэдра и перпендикуляра к этому ребру.

Пусть точка О равноудаленна от всех вершин тетраэдра.

Расстояние от точки О до одной из вершин тетраэдра обозначим R. Сфера с центром О и радиусом R проходит через все данные точки. Из этого доказательства следует, что такая сфера может быть только одна.

Что и требовалось доказать. б) Рассмотрим двугранный угол. Геометрическое место точек, равноудаленных от обеих граней двугранного угла, это плоскость, которая делит двугранный угол пополам. Значит центр сферы, вписанной в тетраэдр, равноудален от всех граней пирамиды, и он должен принадлежать каждой из биссекторных плоскостей, то есть это точка пересечения биссекторных плоскостей всех двугранных углов тетраэдра. Т.к. все точки биссекторной плоскости лежат между гранями двугранного угла, то центр сферы, вписанной в тетраэдр, всегда находится внутри тетраэдра.

Центр у вписанной сферы может быть только один. Сфера с радиусом, равным расстоянию от этой точки до плоскости какой-либо грани тетраэдра, касается всех граней тетраэдра. Следовательно, в любой тетраэдр можно вписать сферу и притом только одну.

Теперь докажем 2 факта, которые использовались в доказательстве.

1) В любой трехгранный угол можно вписать сферу.

2) Биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.

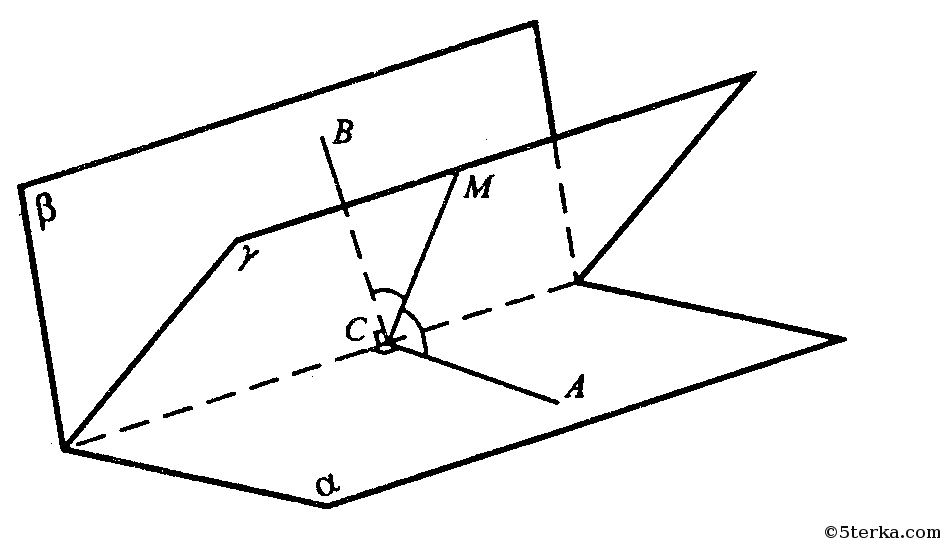
∠AСB — линейный угол двугранного угла между плоскостями α и β.

Пусть γ делит этот двугранный угол так, что ∠BСМ=∠АСМ. Таким образом, γ биссекторная плоскость данного двугранного угла.

Докажем, что биссекторные плоскости двугранных углов трехгранного угла пересекаются по одному лучу.

β₁ и β₂ — биссекторные плоскости, их пересечение — луч, с началом в точке S — вершине тетраэдра. Луч обозначим 1. Пусть точка А ∈ l, A — произвольная точка луча. Проведем перпендикуляры АА₁, АА₂, АА₃ на грани трехгранного угла. А ∈ β₁ таким образом,

Тогда, АА₁=АА₂=АА₃, то есть точка А равноудалена от плоскостей граней NSB и MSB. Значит, точка А находится на биссек-торной плоскости двугранного угла с ребром SP. А т.к. точка А произвольная точка, то и весь луч находится в биссекторной плоскости.

Значит, все три биссекторные плоскости пересекаются по одному лучу, любая точка которых равноудалена.

2. Пусть l — луч, по которому пересекаются биссекторные плоскости трехгранного угла при вершине А, М — точка пересечения луча l и грани BDC.

отрезка АМ принадлежат разным граням двугранного угла при ребре ВС, поэтому биссекторная плоскость этого двугранного угла пересечет отрезок АМ в точке О ∈ l, поэтому она равноудалена от плоскостей АВС и ABD и AСD. Расстояние от точки О до плоскостей АВС и BСD равны, т.к. точка О принадлежит биссекторной плоскости двугранного угла при ребре ВС. Таким образом, точка О равноудалена от всех граней тетраэдра, то есть принадлежит всем биссекторным плоскостям двугранных углов тетраэдра. Таким образом, биссекторные плоскости двугранных углов тетраэдра пересекаются в одной точке.

Оба утверждения доказаны.

Источник

Сфера, вписанная в пирамиду

Биссекторная плоскость. Основное свойство биссекторной плоскости

Определение 1. Биссекторной плоскостью двугранного угла называют такую плоскость, которая проходит через ребро двугранного угла и делит этот угол на два равных двугранных угла (рис. 1).

Утверждение 1. Точка, расположенная внутри двугранного угла, находится на одном и том же расстоянии от граней этого угла тогда и только тогда, когда она лежит на биссекторной плоскости.

Таким образом, справедливость утверждения вытекает из соответствующих теорем о свойствах биссектрисы угла. Доказано.

Следствие 1. Если сфера, расположенная внутри двугранного угла, касается каждой из плоскостей граней этого угла, то центр сферы находится на биссекторной плоскости двугранного угла (рис. 3).

Сфера, вписанная в пирамиду. Свойства пирамиды, описанной около сферы

Определение 2. Сферой, вписанной в пирамиду, называют такую сферу, которая касается плоскостей всех граней пирамиды, причем точки касания лежат на гранях пирамиды (рис. 4).

Определение 3. Если сфера вписана в пирамиду, то пирамиду называют описанной около сферы.

Если сфера вписана в пирамиду, то она касается граней каждого внутреннего двугранного угла, образованного соседними гранями пирамиды. В соответствии со следствием 1 центр вписанной в пирамиду сферы должен находиться в точке пересечения биссекторных плоскостей всех внутренних двугранных углов, образованных соседними гранями пирамиды.

Если у пирамиды нет точки, в которой пересекаются биссекторные плоскости всех внутренних двугранных углов, образованных соседними гранями пирамиды, то в такую пирамиду нельзя вписать сферу.

Замечание 1. Для того, чтобы проверить, можно ли в пирамиду вписать сферу, достаточно проверить, существует ли точка пересения биссекторных плоскостей всех внутренних двугранных углов при основании пирамиды. Если такая точка существует, то она будет равноудалена как от основания пирамиды, так и от каждой из боковых граней.

Рассмотрим несколько типов пирамид, в которые можно вписать сферу.

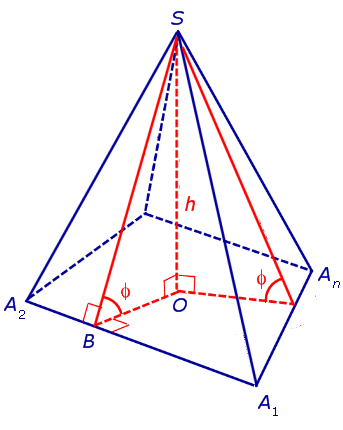
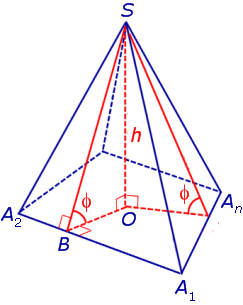
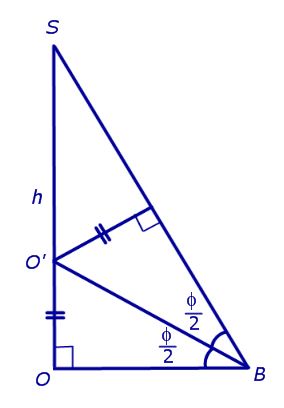
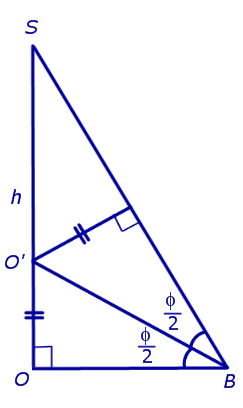
Катет OB прямоугольного треугольника SOB выражается через высоту пирамиды h и угол φ по формуле

Катет OO’ прямоугольного треугольника OO’B выражается через высоту пирамиды h и угол φ по формуле

Поскольку длина отрезка OO’ не зависит от выбора боковой грани пирамиды, то биссекторные плоскости всех внутренних двугранных углов при основании пирамиды пересекаются в точке O’, которая и является центром вписанной в пирамиду сферы.

Доказательство утверждения 2 завершено.

Поскольку у любой правильной пирамиды все внутренние двугранные углы при основании равны, то справедливо

Следствие 2. В любую правильную пирамиду можно вписать сферу, причем ее радиус R выражается через высоту пирамиды h и внутренний двугранный угол при основании пирамиды φ по формуле

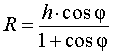(1)

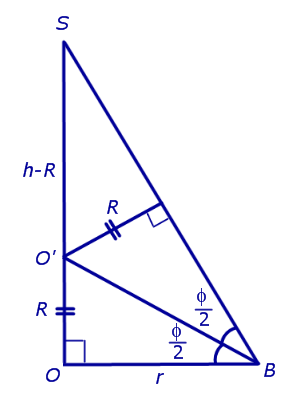
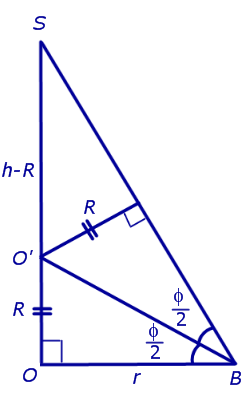
Буквой R на рисунке 7 обозначен радиус вписанной в пирамиду сферы, буквой r – радиус вписанной в основание пирамиды окружности, а буквой φ – внутренний двугранный угол при основании пирамиды. Из прямоугольного треугольника OSB получаем

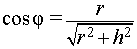(2)

В силу следствия 2 из формул (1) и (2) получаем

из формулы (3) получаем соотношение

Ответ.

Следствие 3. Радиус сферы, вписанной в правильную треугольную пирамиду с высотой h и ребром основания a, равен

Следствие 4. Радиус сферы, вписанной в правильный тетраэдр с ребром a, равен

Следствие 5. Радиус сферы, вписанной в правильную четырехугольную пирамиду с высотой h и ребром основания a, равен

Следствие 6. Радиус сферы, вписанной в правильную шестиугольную пирамиду с высотой h и ребром основания a, равен

Сфера, вписанная в треугольную пирамиду.
Формула для радиуса вписанной сферы

Утверждение 3. В любую треугольную пирамиду можно вписать сферу.

Доказательство. Доказательство этого утверждения напоминает планиметрическое доказательство возможности вписать окружность в произвольный треугольник.

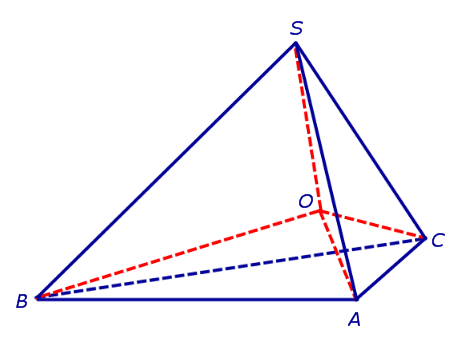
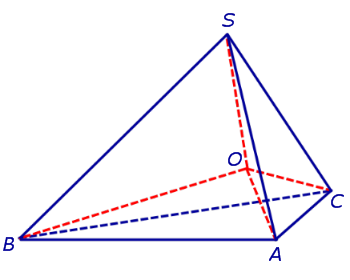
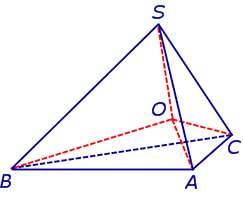
Получим формулу, позволяющую вычислить радиус вписанной в тетраэдр SABC сферы. Для этого заметим, что объем пирамиды SABC равен сумме объемов пирамид OABC, OSCA, OSAB, OSCB, причем высота каждой из пирамид OABC, OSCA, OSAB, OSCB равна радиусу R вписанной в пирамиду SABC сферы. Если обозначить площади граней тетраэдра SABC символами

а объемы пирамид SABC, OABC, OSCA, OSAB, OSCB – символами

то справедливы следующие равенства:

где символом S_полн обозначена площадь полной поверхности пирамиды SABC.

Замечание 2. Если в пирамиду (необязательно треугольную) можно вписать сферу, то, рассуждая аналогично, можно получить следующую формулу для радиуса вписанной в пирамиду сферы

где символами V_пир и S_полн обозначены объем и площадь полной поверхности пирамиды соответственно.

Источник

Как вписать сферу в тетраэдр

ТЕТРАЭДР. ВИДЫ ТЕТРАЭДРОВ

Тетраэдр является одним из простейших многогранников, гранями которого являются четыре треугольника. Его можно считать пространственным аналогом треугольника. Рассмотрим свойства треугольников и аналогичные им свойства тетраэдров.
Теорема 1. Биссектрисы треугольника пересекаются в одной точке – центре вписанной окружности.
Теорема 1′. Биссектральные плоскости двугранных углов тетраэдра пересекаются в одной точке – центре вписанной сферы.
Доказательство. Пусть ABCD – тетраэдр. Пересечением биссектральных плоскостей двугранных углов с ребрами AB, AC,и BC (рис. 1) является точка O, равноудаленная от всех граней тетраэдра. Следовательно, эта точка принадлежит биссектральным плоскостям остальных двугранных углов тетраэдра и является центром вписанной сферы.

Теорема 9′ (Чевы). Пусть на ребрах AB, BC, CD и AD тетраэдра ABCD взяты соответственно точки A ₁ , B ₁ , C ₁ и D ₁. Плоскости ABC ₁ , BCD ₁ , CDA ₁ и DAB ₁ пересекаются в одной точке тогда и только тогда, когда

Рассмотрим теперь некоторые специальные тетраэдры.
Равногранным тетраэдром называется тетраэдр, у которого все грани равны.
Теорема 10. Для любого остроугольного треугольника существует равногранный тетраэдр, грани которого равны данному треугольнику.
Доказательство. Пусть ABC – произвольный остроугольный треугольник. Через его вершины проведем прямые, параллельные противоположным сторонам (рис. 5).

Покажем обратное, пусть ABCD – равногранный тетраэдр, O – цетр описанной сферы. Тогда плоскости граней пересекают описанную сферу по окружностям одинакового радиуса. Следовательно, расстояния от точки O до граней тетраэдра равны и, значит O – центр вписанной сферы.
Прямоугольным тетраэдром называется тетраэдр, у которого все плоские углы при какой-нибудь вершине прямые.
Теорема 12. Основанием высоты прямоугольного тетраэдра, проведенной из вершины с прямыми плоскими углами, является точка пересечения высот противоположной грани.
Теорема 13. (Пифагора) Квадрат площади грани прямоугольного тетраэдра, лежащей против вершины с прямыми плоскими углами, равен сумме квадратов площадей остальных граней этого тетраэдра.
Доказательство. Пусть ABCD – прямоугольный тетраэдр (рис. 7). Плоские углы при вершине D прямые. Можно было бы обозначить ребра, выходящие из вершины D через a, b, c, а затем воспользоваться формулой Герона для нахождения площади треугольника ABC .

Тогда A ₁ B ₁ D ₁ C ₁ – параллелограмм. Его диагонали равны тогда и только тогда, когда он – прямоугольник, т.е. AC BD .
Теорема 2. Тетраэдр является ортогональным тогда и только тогда, когда он является ортоцентрическим.
Доказательство. Пусть ABCD – ортогональный тетраэдр (рис. 9). DD ₂ – высота, опущенная из вершины D. Плоскость CDD ₂ перпендикулярна AB и, следовательно, DC ₁ и CC ₁ – высоты треугольников ABC и ABD. Высоты DD ₂ и CC ₂ треугольника C ₁ CD пересекаются.

Литература
1. Адамар Ж. Элементарная геометрия. Часть II. Стереометрия. – М.: Учпедгиз, 1938.
2. Перепелкин Д.И. Курс элементарной геометрии. Часть II. Геометрия в пространстве. – М.-Л.: Гостехиздат, 1949.
3. В.В.Прасолов, И.Ф.Шарыгин. Задачи по стереометрии. – М.: Наука, 1989.
4. Д.О.Шклярский, Н.Н.Ченцов, И.М.Яглом. Избранные задачи и теоремы элементарной математики. Часть 3. – М.: Государственное издательство технико-теоретической литературы, 1954.

Источник