Как врезать пирамиду в куб

Врезка пирамиды и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку пи­рамиды и цилиндра.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Изобразите пирамиду и цилиндр (рис. 5.152). Пред­ставьте линию врезки. Наклонные грани пирамиды рассекают цилиндр по эллипсам. Сечение цилинд­ра основанием пирамиды — окружность. Сечение пирамиды верхним основанием цилиндра — квадрат, подобный квадрату основания пирамиды. Из всех этих сечений, пожалуй, наиболее сложные — сече­ния цилиндра наклонными плоскостями.
Для построения таких сечений необходимы две вспомогательные вертикальные секущие плоско­сти, проходящие через ось цилиндра. Эти плоско­сти перпендикулярны друг другу и наклонным гра­ням пирамиды (рис. 5.153 и 5.154).

Постройте сначала линию пересечения цилин­дра и наклонной грани пирамиды, выделенной на рис. 5.155.

Найдите такое ее положение, которое даст гармоничные соотношения поверхностей гео­метрических тел. Зафиксируйте нижнюю точку се­кущего эллипса — точку А на пересечении верти­кальной вспомогательной плоскости и наклонной грани пирамиды (рис. 5.156), постройте сечение (рис. 5.157).

После построения первой линии сечения взаим­ное положение геометрических тел стало опреде­ленным, что дает возможность построить остальные
линии сечения.
Вариантов дальнейшего построения может быть несколько. Например, если достроить сечение пи­рамиды вспомогательной плоскостью, которую мы уже использовали в построении наклонного сече­ния, то можно получить несколько опорных точек (рис. 5.158). Точки В и С определяют положение ли­нии сечения пирамиды верхним основанием цилин­дра, точка О — центр окружности сечения цилиндра горизонтальной плоскостью основания пирамиды, а точки D и Е — раскрытие эллипса этого сечения на вашем рисунке.

Постройте горизонтальное сечение цилиндра (рис. 5.159), а затем по опорным точкам на пере­сечении пирамиды и второй вспомогательной се­кущей плоскости (рис. 5.160) постройте сечение цилиндра второй наклонной гранью пирамиды (рис. 5.161). В этом задании мы ограничимся пост­роением только видимых линий сечения. Однако, при необходимости, вы можете построить все ли­нии. Затем усильте основные линии рисунка (рис. 5.162) и тонируйте связку (рис. 5.163).

Можно предложить и другую последователь­ность построения. Она уместна тогда, когда положе­ние геометрических тел заранее определено, на­пример, в ортогональных проекциях (рис. 5.164). В этом случае лучше начать построение с вертикаль­ного цилиндра. Задайте перспективные направле­ния при помощи двух вертикальных секущих плос­костей (рис. 5.165) — эти плоскости впоследствии пригодятся нам в построении наклонных сечений.
Чтобы изобразить пирамиду, определите, где плос­кость ее основания пересекает вертикальную ось цилиндра, и постройте секущий эллипс (рис. 5.166).

Определите положение точки центра основания пи­рамиды относительно центра окружности сечения (рис. 5.167), для чего сначала опишите вокруг секу­щего эллипса квадрат. Центр основания пирамиды смещен относительно центра окружности сечения по диагонали этого квадрата примерно на треть ра­диуса (это следует из плана). Нарисуйте квадрат ос­нования пирамиды. Из точки пересечения диагона­лей квадрата поднимите вертикаль, отложите на ней высоту пирамиды и достройте наклонные ребра (рис. 5.168). Таким образом мы получили связку с точным положением геометрических тел в про­странстве.

Теперь достройте линию сечения. Чтобы пост­роить сечение цилиндра наклонными гранями пира­миды, воспользуйтесь вспомогательными вертикальными секущими плоскостями, проходящими че­рез вертикальную ось цилиндра (мы изобразили их в самом начале построения). Выберите любую вспомогательную плоскость. Линия сечения этой плоскостью цилиндра — вертикальный прямоуголь­ник. Линия сечения пирамиды этой же вспомога­тельной плоскостью — трапеция. На рис. 5.169 пря­моугольник и трапеция графически выделены тоном и толстой линией. На пересечении прямоугольника и трапеции получите опорные точки, необходимые для дальнейшего построения. Изобразите наклон­ное сечение цилиндра. Затем проделайте эти же действия с другой вспомогательной секущей плос­костью (рис. 5.170).

Закончите построение (рис. 5.171) и тонируйте связку (рис. 5.172).

Источник

Врезка куба и пирамиды

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и пирамиды. Оценить многообразие возможных связок куба и пирамиды, отработать приемы построения их врезок, научиться создавать на листе связки с гармоничными пропорциями.

ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и пирамиды сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее красивые, гармоничные пропорции связок, изменяя положение линии пересечения геометрических тел.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

Рассмотрите ортогональные проекции двух геометрических тел – куба и пирамиды – на рис. 5.20. Представьте взаимное положение тел. Изобразите в перспективе заданную связку куба и пирамиды с различным положением относительно линии горизонта (выше линии горизонта на рис. 5.21 и ниже линии горизонта на рис. 5.22).

Изобразите куб и пирамиду в положении, представленном на рис. 5.23. Предложите несколько вариантов врезок, например, как на рис. 5.24; 5.25 и
5.26.

Теперь попробуйте сделать подобное упражнение, увеличив количество геометрических тел. Связка тел – куба и трех пирамид – предлагается на рис. 5.27. Когда на рисунке взаимодействуют не два, а четыре геометрических тела, сложнее найти гармонию их объемов и линий пересечения. Постройте врезки, например, как это сделано на рис. 5.28. Легко тонируйте композицию (рис. 5.29 и 5.30).

Другой вариант этого задания представлен на рис. 5.31; 5.32 и 5.33.

Источник

Врезки шара и куба, когда секущие плоскости куба не проходят через центр шара

ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Чтобы научиться изображать врезки шара и куба, когда секущие плоскости куба не проходят через центр шара, сначала нарисуйте сложную врезку шара и куба в произвольном положении, а затем по заданным ортогональным проекциям.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

Рассмотрите рис. 5.80-5.87. Шар последовательно перемещается относительно куба, образуя связки различной сложности, причем каждая следующая связка имеет более сложную в построении линию врезки по сравнению с предыдущей. Для лучшего понимания перемещений шара и геометрии связок рядом с перспективными изображениями представлены ортогональные проекции.

На рис. 5.80 и 5.81 изображена самая простая связка, когда центр шара совпадает с вершиной куба. Построение линии врезки в этом случае сводится к построению трех центральных секущих плоскостей взаимно перпендикулярных направлений, соответствующих граням куба. Такое построение уже было разобрано нами ранее, теперь эта связка для нас – исходное положение для дальнейших построений.

На рис. 5.82 и 5.83 шар смещен вверх. При этом горизонтальная секущая шар плоскость – верхняя грань куба – переместилась вниз. Теперь для пересечения шара с горизонтальной гранью куба необходимо построить дополнительный горизонтальный эллипс, параллельный горизонтальному эллипсу, проходящему через центр шара. Раскрытие этого нового эллипса будет несколько больше раскрытия центрального горизонтального эллипса, так как он расположен дальше от линии горизонта. Полученная линия врезки (как и в исходном положении) замкнута и состоит из сегментов трех различных эллипсов. Точки, в которых один эллипс сменяет другой, лежат на ребрах куба.

На рис. 5.84 и 5.85 шар смещен влево относительно предыдущего положения. Линия врезки теперь пройдет по дополнительному вертикальному эллипсу, соответствующему по своему раскрытию центральному вертикальному эллипсу сечения.

На рис. 5.86 и 5.87 шар смещен назад от зрителя. При этом смещении появляется еще один дополнительный вертикальный эллипс.

Для лучшего освоения материала изобразите рассмотренные связки куба и шара. Причем все четыре изображения могут быть соединены в одном рисунке. Только в этом случае перемещаться будет не шар, а куб. Сначала нарисуйте первую связку, когда центр шара совпадает с вершиной куба. Куб и секущие эллипсы изобразите легкими линиями. Затем на этом же рисунке опустите куб, нарисуйте новый куб и новую линию врезки. Продолжайте перемещать куб. С каждым новым перемещением на вашем рисунке будет появляться новый куб и новый секущий эллипс. Всякий раз незначительно усиливайте линии нового куба по сравнению с предыдущим. Последней связке придайте законченный характер: усильте основные линии и введите в рисунок легкий тон. При построении подобных сложных связок иногда можно и не изображать некоторые секущие эллипсы. Например, на связке, представленной на линейном рис. 5.88, в ортогональных проекциях на рис. 5.89 и в тональном рис. 5.90 сознательно не нарисован один из вертикальных эллипсов сечения, так как он не видим зрителю с данной точки.

Теперь изобразите сложную связку куба и шара, заданную в ортогональных проекциях на рис. 5.91. Нарисуйте куб и найдите точку центра шара, для этого последовательно откладывайте координаты точки от ближайшей к центру шара вершины (рис. 5.92). Опишите окружность заданного диаметра вокруг центра шара.

Постройте три взаимно перпендикулярных сечения шара, проходящих через его центр параллельно граням куба (рис. 5.93).

Изобразите линии пересечения шара и куба. Грани куба рассекают шар по трем окружностям. Чтобы изобразить эти окружности, необходимо сначала найти их центры. Обратитесь к ортогональным проекциям. Центры окружностей сечения – точки А, В и С – проекции центра шара на секущие плоскости (грани куба). Постройте проекции центра шара на секущие плоскости. Искомые точки лежат на пересечении граней куба с прямыми а, в и с, проходящими через центр шара параллельно его ребрам. Последовательно нарисуйте все три эллипса сечения, определяя оси каждого эллипса и точки, через которые он проходит. Проследите за тем, чтобы линия врезки была замкнута, а точки, в которых секущие эллипсы сменяют друг друга, лежали на ребрах куба (рис. 5.94).

Тонируйте связку (рис. 5.95).

Теперь выполните упражнение на создание гармоничных связок куба и шара. Нарисуйте куб и шар в произвольном положении, например, как на рис. 5.96. Предложите несколько вариантов врезок, например, как на рис. 5.97; 5.98 и 5.99. Тонируйте любую связку (рис. 5.100). Для закрепления материала изобразите еще одну связку куба и шара (рис. 5.101) и тонируйте ее (рис. 5.102).

Источник

Математика пирамиды. Строительство садовой пирамиды.

С учётом практической готовности главы №6 «Исторические гипотезы», скоро выходим на финишную прямую. Сегодня публикуется статья «Строительство садовой пирамиды» из 5 главы.

Описываемый тип пирамиды не только видел лично но и некоторое время в ней обитал. Человек в Латвии построил отдыхательный комплекс из 4х таких пирамид и зарабатывал на этом «скромные средства на шпильки и булавки».

Строительство садовой пирамиды.

Поскольку пирамида привязывается к геомагнитной сетке, размер её, при правильной планировке, как правило, кратен ячейкам геомагнитной сети и может быть равен одной ячейке, 3 на 3, 5 на 5, 7 на 7 и так далее. Для больших пирамид, как и для больших букетов цветов, нечётная кратность уже неактуальна.

Повторимся, что центр установки такой пирамиды должен быть на восходящей точке геомагнитной сети. Иначе пирамида или будет неэффективна, или вообще не будет работать. Поэтому, нужно определить при помощи встроенного в качественный смартфон магнитометра и бесплатного приложения «Water detector» геомагнитную сеть, оттеститовать четыре прямоугольником лежащие ближайшие точки и выбрать ту точку, у которой проявляется максимальный эффект по утрам. Методику мы уже описывали ранее.

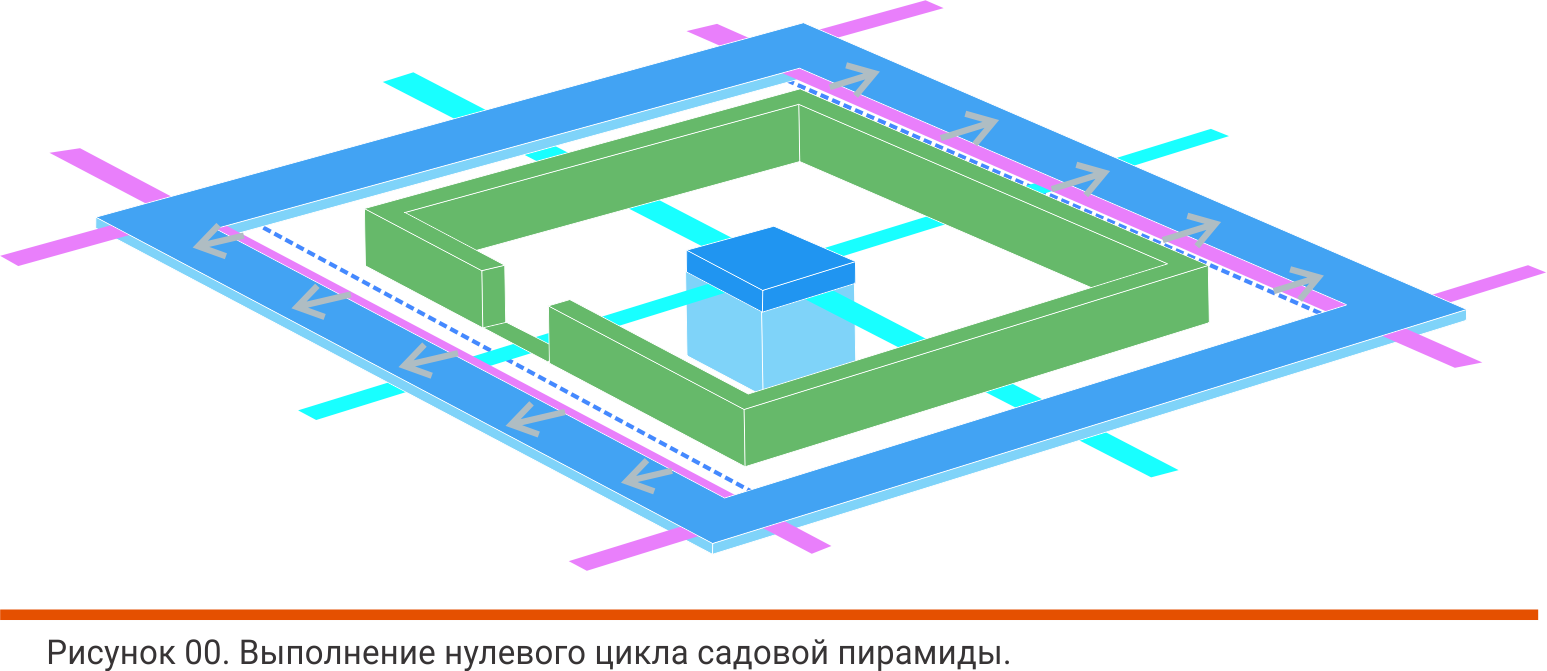
Для этого подручными средствами выкапываем на оси будущей пирамиды куб около 50х50х50 см, бросаем туда достаточное количество (не менее 15% объёма) мелкого лома чёрных металлов и заливаем его бетоном под нулевой уровень. У кого есть возможность, вместо лома металлов можно добавлять железосодержащие породы, металлургический шлак, магнетит или пирит в тех же пропорциях по содержанию железа и его окислов.

Скорее всего, над отверстием делается опалубка высотой в одну доску, чтобы этот бетонный куб был чуть выше уровня земли. Почва под пирамидой в этом случае не будет получать достаточно света, плодородный слой земли лучше предварительно удалить для использование в другом месте.

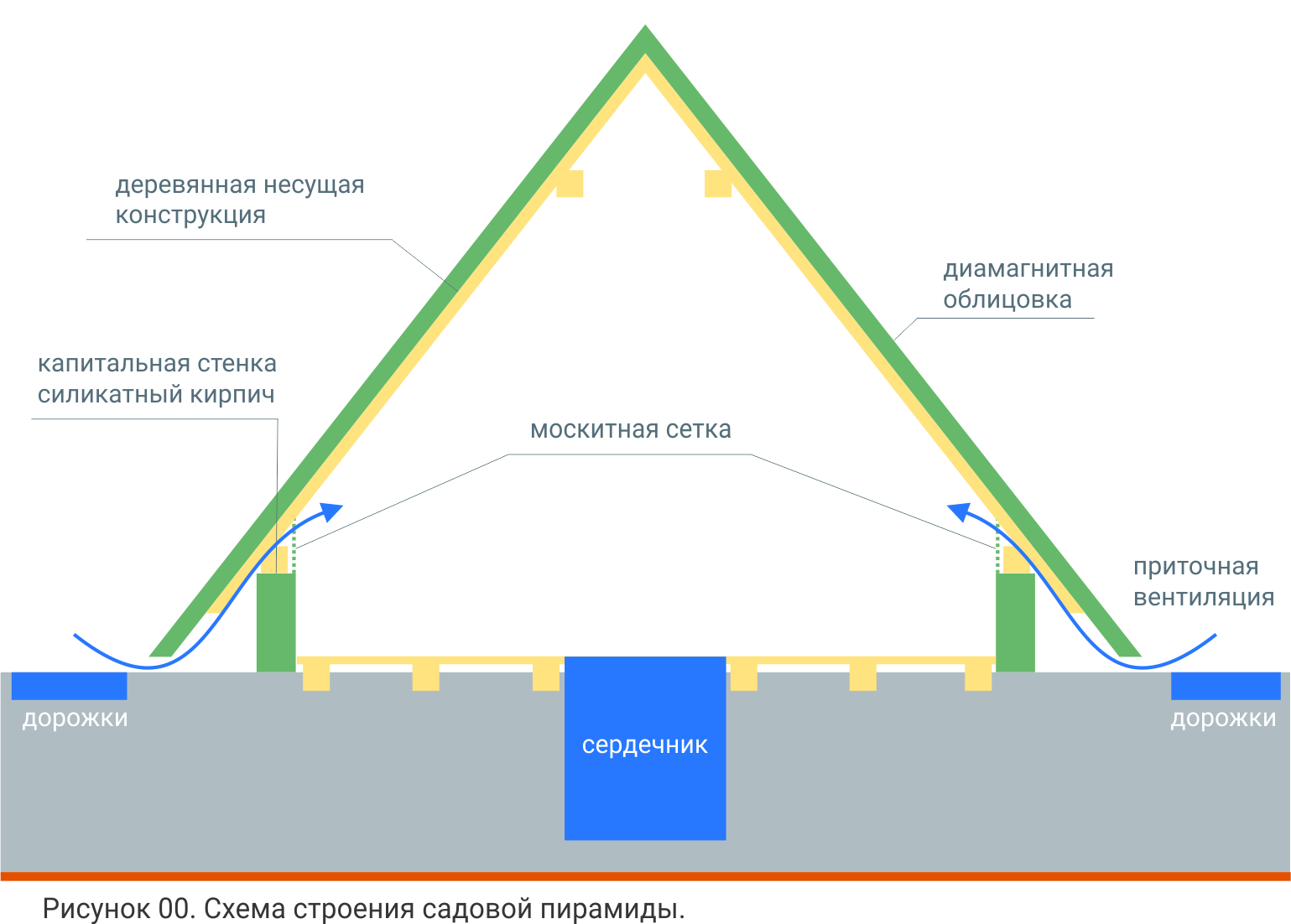
Поскольку у пирамиды парамагнитным носителем заряда является кислород, необходимо предусмотреть также вентиляцию такой пирамиды. Поэтому, пирамида, образно говоря, будет представлять собой одну большую крышу на очень небольших стенках, между которыми и «крышей» будет устроен вентиляционный зазор. При этом внешний периметр пирамиды также не будет соединён с землёй для образования притока воздуха.

Поскольку мы установили посреди пирамиды парамагнитную «аномальную зону», она будет удерживать на месте «крест» восходящих потоков. В то же время, она вполне вероятно может сместить к себе сетку нисходящих потоков, образовав «подушкообразное» искривление геомагнитной сетки. Тогда эти потоки могут оказаться под куполом пирамиды и значительно снизить её эффективность в дневное время.

Чтобы этого не произошло, по периметру пирамиды, как раз по разметке геомагнитной сети, которую мы делали ещё до строительства пирамиды, делается парамагнитная дорожка из бетона с добавлением магнетита или ферритовой стружки или других железосодержащих материалов. Дорожка может быть также выполнена из самостоятельно изготовленной тротуарной плитки с тем же железосодержащим парамагнитным составом. Выполняется она с тем расчётом, чтобы по ней можно было ходить босиком. Эта дорожка входит в комплекс пирамиды, по ней днём будут идти положительные ионные потоки, и хождение днём по такой дорожке также будет полезным для человека. При этом, общем случае, эта дорожка будет не квадратной, а прямоугольной, поскольку частота сетки с севера на юг и с запада на восток, в общем случае, различна. В средней полосе такая дорожка будет иметь размеры около 4 на 5 метров. Поэтому с северной и южной сторон, чтобы она не заходила под крышу пирамиды, её можно сместить на 30 см к югу и северу от пирамиды

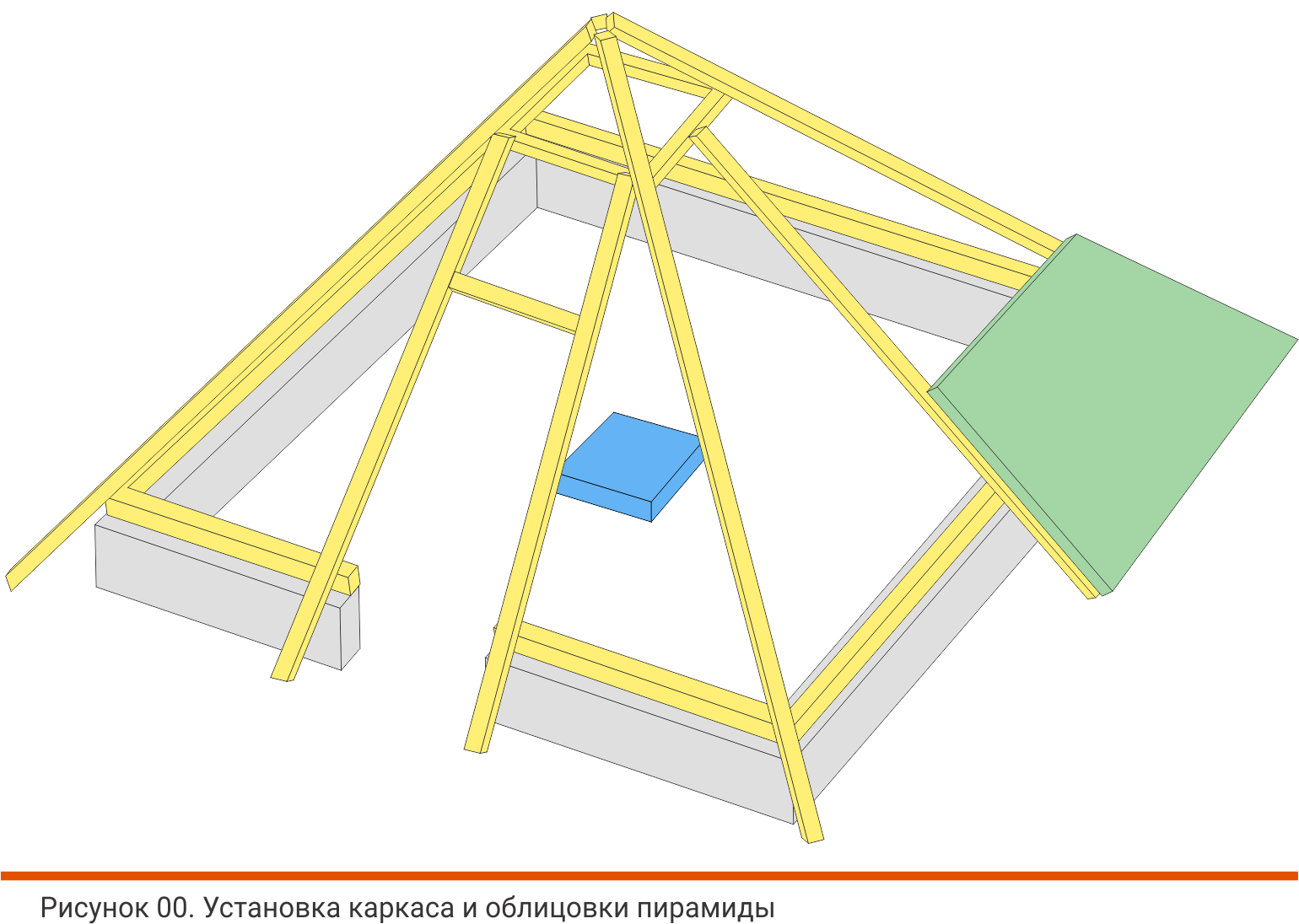
То же относится и к несущему каркасу самой пирамиды. Начинается он с кольцевого бруса по всему торцу несущей стенки, а дальше выполняется обычный кровельный деревянный каркас. Если диамагнитный материал облицовки имеет небольшие физические размеры, не позволяющие его крепить непосредственно на каркас пирамиды, то на каркас пирамиды крепятся листы влагостойкой фанеры или ОСП. Крепёж также должен осуществляться без применения металлических элементов, или они могут использоваться временно для закрепления склеиваемых деталей. После склеивания они должны быть удалены. Вполне можно использовать нейлоновый крепёж. Его можно потом не удалять.

Поэтому, оставляя поликарбонат, как возможный материал, можно рассмотреть другие варианты. Интересным вариантом является экструдированный пенополистирол. Обладая достаточной жёсткостью, теплоизоляционными качествами и прекрасной диамагнитной характеристикой, экструдированный пенополистирол подходит для сооружения трёхсезонной (весна-лето-осень) пирамиды.

Так как проводить сетевое электричество в пирамиду можно, но не рекомендуется, для освещения можно остановиться на автономных уличных солнечных светильниках со встроенным аккумулятором в пластиковом корпусе, немного их модифицировав. Расположив их основной корпус с электрогенерирующей частью на южной или западной внешних гранях пирамиды нужно демонтировать из этих корпусов световые панели и завести их в саму пирамиду. Образовавшиеся проёмы в корпусах светильников можно закрыть куском пластика на клею или силиконе для герметичности. Так мы будем иметь автоматическое автономное освещение в пирамиде в течении нескольких часов после заката.

Источник

Как врезать цилиндр в пирамиду

Начертательная геометрия

Пересечение прямого кругового цилиндра с поверхностью пирамиды.

На рис 17 показано пересечение цилиндра и правильной шестиугольной пирамиды. Сначала определяется на каких проекциях нужно строить линию пересечения. Затем определяют характерные точки. Дополнительные точки строятся с помощью вспомогательных горизонтальных плоскостей.

Раздел 5 Взаимное пересечение поверхностей двух тел вращения.

5.1 Пересечение поверхностей цилиндров.

Построение линии пересечения цилиндров начинают со сравнения их оснований. На рис. 18 изображены три вертикальных цилиндра (А,Б,В) разных диаметров, которые пересекаются с половиной горизонтального цилиндра.

Рассмотрим, какая получается линия пересечения в зависимости от соотношения диаметров цилиндров. Если пересекаются два цилиндра разных диаметров, то линия их пересечения представляет собой кривую, кривизна которой зависит от разности диаметров. Чем больше разность, тем меньше кривизна, и наоборот. При этом изгиб кривой всегда идет в сторону большего диаметра, так как цилиндр с меньшим диаметром как бы проходит через цилиндр с большим диаметром. Если же диаметры одинаковые, то линия пересечения изображается прямыми линиями, имея форму эллипсов.

5.2 Построение пересечения поверхностей тел вращения с помощью вспомогательных секущих плоскостей.

Линии пересечения тел вращения обычно строят с помощью вспомогательных секущих плоскостей Р (рис. 19). Каждая плоскость пересекает одновременно оба тела вращения по соответствующим линиям. Эти линии пересекаются между собой в точках, определяющих линию пересечения заданных поверхностей. Количество вспомогательных плоскостей берется в зависимости от требуемой точности построения.

Еще один пример на рис. 20. Здесь рассматривается построение линии пересечения конуса и шара. Вспомогательные плоскости — фронтально-прецирующие плоскости N, R, Т, М.

Вписанный в пирамиду цилиндр. Цилиндр и пирамида: варианты комбинаций

Одними из интересных задач, которые позволяют сравнить различные объемные фигуры, являются задачи на описание одной из них около другой. В данной статье рассмотрим различные варианты описанного около пирамиды и вписанного в пирамиду цилиндра.

Пирамида в геометрии

Прежде чем изучать комбинации вписанного в пирамиду цилиндра и вписанной пирамиды в цилиндр, следует рассмотреть эти фигуры с точки зрения геометрии. Начнем с пирамиды.

Фигура пирамида представляет собой тело в пространстве, которое получается, если соединить все вершины произвольного плоского n-угольника с некоторой точкой в пространстве. При этом n-угольник может быть совершенно произвольным (выпуклым, вогнутым, правильным, с различным количеством сторон n). На положение отмеченной точки накладывается одно единственное условие: она не должна лежать в той плоскости, в которой n-угольник находится.

На рисунке выше показана, пожалуй, самая известная пирамида — четырехугольная. Видно, что вершины четырехугольника, который называется основанием фигуры, соединены с точкой, лежащей над ним. Эта точка называется вершиной пирамиды.

Приведенное определение и также представленный рисунок свидетельствуют, что любая пирамида, независимо от типа ее основания, будет включать в себя n треугольников. Все они соединяются в вершине фигуры.

Перпендикулярный отрезок, проведенный из вершины фигуры к ее основанию, называется высотой. Если высота пересекает в геометрическом центре n-угольник, то такая пирамида будет прямой. В противном случае имеет место наклонная фигура.

Если все стороны n-угольника равны между собой, и фигура является прямой, то ее называют правильной. Именно с правильными пирамидами удобно работать при изучении их взаимного расположения с другими объемными телами в геометрии.

Цилиндр в геометрии

Цилиндр в общем случае можно получить, если вдоль замкнутой кривой перемещать отрезок параллельно самому себе таким образом, чтобы отрезок не лежал в плоскости этой кривой. Этот отрезок называется образующей цилиндра, а кривая, вдоль которой он перемещается, носит название направляющей.

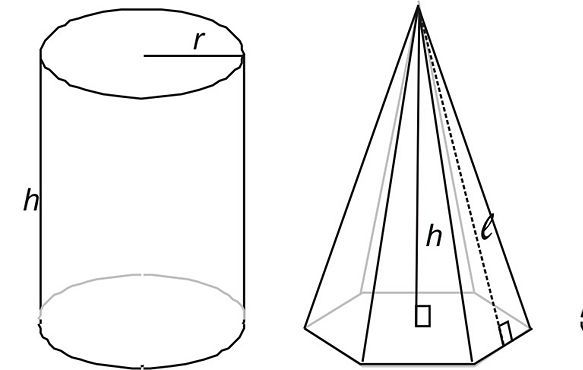
Если направляющая является окружностью, а образующая ей перпендикулярна, то полученный цилиндр будет называться прямым с круглым основанием. Эта фигура известна каждому. Она представлена на рисунке ниже.

Далее будем рассматривать только прямой круглый цилиндр.

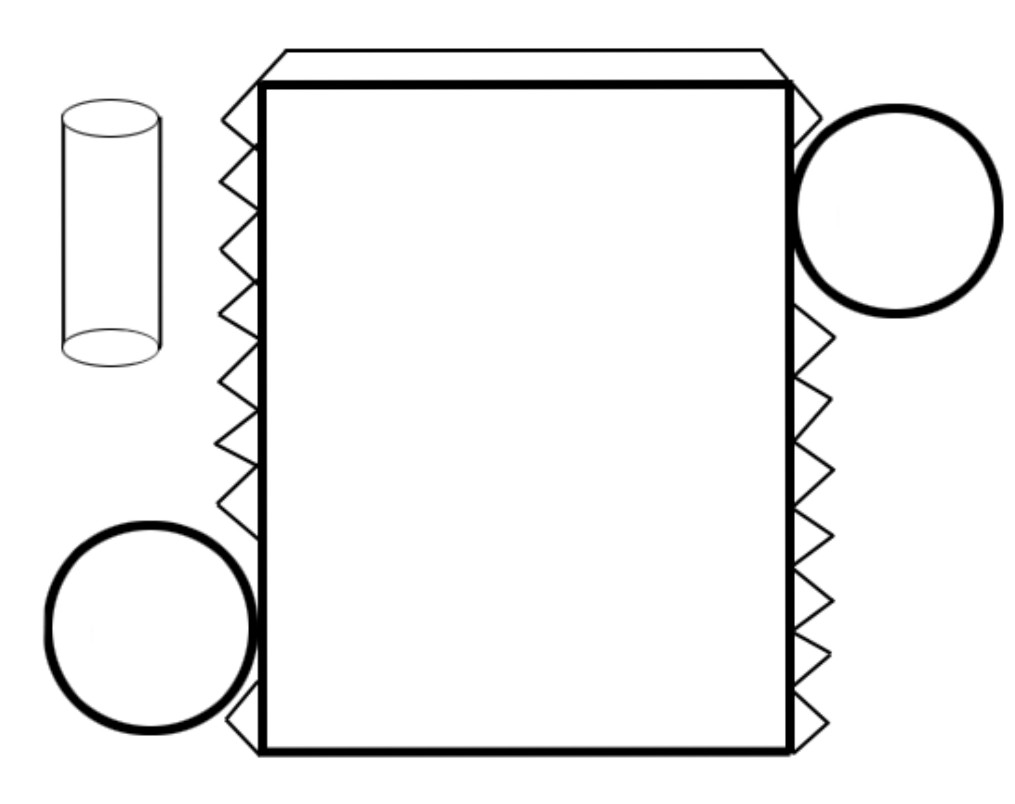
В отличие от пирамиды, цилиндр не имеет вершин и ребер. Однако он образован двумя основаниями (два одинаковых круга, находящихся в параллельных плоскостях) и боковой цилиндрической поверхностью. Если посмотреть на развертку этой фигуры, то можно увидеть, что она состоит из двух кругов и одного прямоугольника (см. рис. ниже).

Основными характеристиками цилиндра являются следующие:

Многоугольник и окружность

Последний вопрос, который следует изучить перед тем, как рассматривать вписанный в пирамиду цилиндр и описанный около нее, связан с взаимным расположением правильного многоугольника и окружности.

Существуют всего два варианта расположения этих плоских фигур:

Приведем формулы, позволяющие вычислить длину стороны многоугольника через радиус окружности. Рассмотрим для примера только два первых многоугольника, то есть равносторонний треугольник и квадрат.

Если окружность проходит через все вершины n-угольника, то говорят, что она его описывает. При известном радиусе R длина стороны вычисляется по формуле:

То есть сторона квадрата, вписанного в окружность с радиусом R, будет немного меньше таковой для равностороннего треугольника, описанного той же окружностью.

Если окружность касается каждой из сторон n-угольника, то говорят, что она вписана в него. В случае правильных многоугольников точка касания фигур находится точно посередине каждой стороны n-угольника. Если известен радиус r окружности вписанной, тогда сторона n-угольника определится по формуле:

То есть вокруг окружности фиксированного радиуса можно описать треугольник с большей длиной стороны, чем квадрат.

Треугольная пирамида, вписанная в цилиндр

Сначала рассмотрим более простой вариант, то есть когда пирамида находится внутри цилиндра. Разберем конкретный пример с правильной треугольной пирамидой. Предположим, что известен радиус R цилиндра и его высота h. Необходимо найти характеристики правильной треугольной пирамиды, вписанной в цилиндр.

Выше уже была приведена формула для стороны равностороннего треугольника, находящегося внутри окружности. Длина его стороны является длиной основания пирамиды. Она равна:

Вершина пирамиды вписанной лежит точно в центре верхнего основания цилиндра, поэтому высоты обеих фигур равны.

Зная длину стороны основания и высоту правильной пирамиды треугольной, можно рассчитать другие ее характеристики. Например, объем вычисляется по формуле:

Длину бокового ребра a_b можно рассчитать так:

Пирамида четырехугольная, вписанная в цилиндр

Как и в предыдущем случае, пирамида находится внутри цилиндра. Только теперь ее основание представляет собой квадрат, сторона которого через радиус R цилиндра вычисляется так:

Высота пирамиды равна таковой для цилиндра, то есть h.

Длина бокового ребра a_b составляет:

Заметим, что формула для длины бокового ребра получилась точно такой же, как в случае треугольной пирамиды.

Цилиндр вписан в фигуру

Цилиндр, вписанный в пирамиду, представляет более сложный случай расположения этих фигур. Чтобы рассчитать размеры пирамиды по известному радиусу и высоте цилиндра, следует разобраться, как этот цилиндр будет расположен внутри нее.

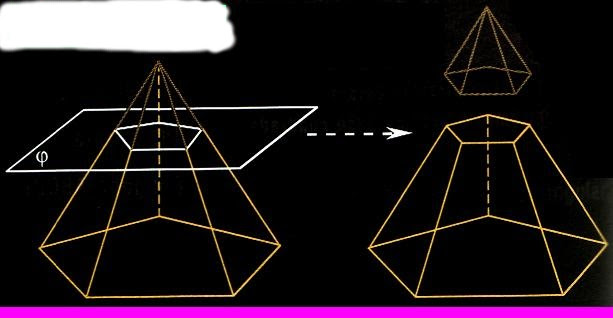
Предположим, что имеется плоскость, параллельная основанию пирамиды. Пересечем этой плоскостью боковую поверхность фигуры. Образованное сечение будет представлять точно такой же многоугольник, что лежит в основании, но меньшего размера. Этот многоугольник будет описывать верхнее основание цилиндра. Нижнее основание будет лежать в основании пирамиды.

Чтобы найти длину стороны многоугольника сечения, следует воспользоваться функцией зависимости площади сечения от вертикальной координаты z. Эта функция имеет вид:

Здесь z — расстояние от основания пирамиды вдоль ее высоты, h_p — высота пирамиды.

Как пользоваться этой формулой для определения параметров описанной около цилиндра пирамиды, покажем на примере решения задачи.

Задача с четырехугольной пирамидой и цилиндром

Известно, что цилиндр имеет радиус r = 5 см и высоту h = 6 см. Найти высоту и сторону правильной четырехугольной пирамиды, описывающей его.

Верхнее основание цилиндра должно вписываться в квадратный срез на высоте h = 6 см от основания пирамиды. Тогда площадь сечения равна:

Здесь a — сторона основания пирамиды. Если взять квадратный корень из S(6), то получим длину стороны квадрата сечения. Она должна быть равна 2*r, чтобы основание цилиндра могло вписаться в это сечение, тогда получаем:

Отсюда получаем выражение:

Таким образом, вписать цилиндр, заданный условием задачи, можно не в одну единственную правильную четырехугольную пирамиду, а в бесконечное их число. Однако параметры каждой из них должны удовлетворять выражению выше, которое связывает высоту фигуры с длиной стороны ее основания.

Врезка куба и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку куба и цилиндра. Оценить многообразие возможных свя­зок куба и цилиндра, отработать приемы построе­ния их врезок, научиться создавать на листе связки с гармоничными пропорциями.

ПОСТАНОВКА ЗАДАНИЯ. Нарисуйте связки куба и цилиндра сначала по заданным ортогональным проекциям, а затем в произвольном положении по отношению друг к другу. Найдите наиболее краси­вые, гармоничные пропорции связок, изменяя поло­жение линии пересечения геометрических тел.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Рассмотрите ортогональные проекции двух геомет­рических тел — куба и цилиндра — на рис. 5.46. Пред­ставьте взаимное положение тел. Изобразите в пер­спективе заданную связку куба и цилиндра с раз­личным положением относительно линии горизонта (выше линии горизонта на рис. 5.47 и ниже линии горизонта на рис. 5.48).

Изобразите куб и вертикальный цилиндр в поло­жении, представленном на рис. 5.49. Предложите несколько вариантов врезок, например, как на рис. 5.50 и 5.51. Тонируйте любую связку (рис. 5.52).

Изобразите куб и горизонтальный цилиндр (рис. 5.53). Предложите гармоничные врезки, например, как на рис. 5.54 и 5.55 (тон на рис. 5.56).
Теперь попробуйте сделать подобное упражне­ние, увеличив количество геометрических тел. Связка тел — куба и трех цилиндров — предлагается на рис. 5.57. Постройте врезки, например, как это сделано на рис. 5.58. Легко тонируйте композицию (рис. 5.59).

Врезка пирамиды и цилиндра

ЦЕЛЬ ЗАДАНИЯ. Научиться строить врезку тела вращения и тела с наклонными гранями.

ПОСТАНОВКА ЗАДАНИЯ. Постройте врезку пи­рамиды и цилиндра.

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ.

Изобразите пирамиду и цилиндр (рис. 5.152). Пред­ставьте линию врезки. Наклонные грани пирамиды рассекают цилиндр по эллипсам. Сечение цилинд­ра основанием пирамиды — окружность. Сечение пирамиды верхним основанием цилиндра — квадрат, подобный квадрату основания пирамиды. Из всех этих сечений, пожалуй, наиболее сложные — сече­ния цилиндра наклонными плоскостями.
Для построения таких сечений необходимы две вспомогательные вертикальные секущие плоско­сти, проходящие через ось цилиндра. Эти плоско­сти перпендикулярны друг другу и наклонным гра­ням пирамиды (рис. 5.153 и 5.154).

Постройте сначала линию пересечения цилин­дра и наклонной грани пирамиды, выделенной на рис. 5.155.

Найдите такое ее положение, которое даст гармоничные соотношения поверхностей гео­метрических тел. Зафиксируйте нижнюю точку се­кущего эллипса — точку А на пересечении верти­кальной вспомогательной плоскости и наклонной грани пирамиды (рис. 5.156), постройте сечение (рис. 5.157).

После построения первой линии сечения взаим­ное положение геометрических тел стало опреде­ленным, что дает возможность построить остальные
линии сечения.
Вариантов дальнейшего построения может быть несколько. Например, если достроить сечение пи­рамиды вспомогательной плоскостью, которую мы уже использовали в построении наклонного сече­ния, то можно получить несколько опорных точек (рис. 5.158). Точки В и С определяют положение ли­нии сечения пирамиды верхним основанием цилин­дра, точка О — центр окружности сечения цилиндра горизонтальной плоскостью основания пирамиды, а точки D и Е — раскрытие эллипса этого сечения на вашем рисунке.

Постройте горизонтальное сечение цилиндра (рис. 5.159), а затем по опорным точкам на пере­сечении пирамиды и второй вспомогательной се­кущей плоскости (рис. 5.160) постройте сечение цилиндра второй наклонной гранью пирамиды (рис. 5.161). В этом задании мы ограничимся пост­роением только видимых линий сечения. Однако, при необходимости, вы можете построить все ли­нии. Затем усильте основные линии рисунка (рис. 5.162) и тонируйте связку (рис. 5.163).

Можно предложить и другую последователь­ность построения. Она уместна тогда, когда положе­ние геометрических тел заранее определено, на­пример, в ортогональных проекциях (рис. 5.164). В этом случае лучше начать построение с вертикаль­ного цилиндра. Задайте перспективные направле­ния при помощи двух вертикальных секущих плос­костей (рис. 5.165) — эти плоскости впоследствии пригодятся нам в построении наклонных сечений.
Чтобы изобразить пирамиду, определите, где плос­кость ее основания пересекает вертикальную ось цилиндра, и постройте секущий эллипс (рис. 5.166).

Определите положение точки центра основания пи­рамиды относительно центра окружности сечения (рис. 5.167), для чего сначала опишите вокруг секу­щего эллипса квадрат. Центр основания пирамиды смещен относительно центра окружности сечения по диагонали этого квадрата примерно на треть ра­диуса (это следует из плана). Нарисуйте квадрат ос­нования пирамиды. Из точки пересечения диагона­лей квадрата поднимите вертикаль, отложите на ней высоту пирамиды и достройте наклонные ребра (рис. 5.168). Таким образом мы получили связку с точным положением геометрических тел в про­странстве.

Теперь достройте линию сечения. Чтобы пост­роить сечение цилиндра наклонными гранями пира­миды, воспользуйтесь вспомогательными вертикальными секущими плоскостями, проходящими че­рез вертикальную ось цилиндра (мы изобразили их в самом начале построения). Выберите любую вспомогательную плоскость. Линия сечения этой плоскостью цилиндра — вертикальный прямоуголь­ник. Линия сечения пирамиды этой же вспомога­тельной плоскостью — трапеция. На рис. 5.169 пря­моугольник и трапеция графически выделены тоном и толстой линией. На пересечении прямоугольника и трапеции получите опорные точки, необходимые для дальнейшего построения. Изобразите наклон­ное сечение цилиндра. Затем проделайте эти же действия с другой вспомогательной секущей плос­костью (рис. 5.170).

Закончите построение (рис. 5.171) и тонируйте связку (рис. 5.172).

Источник