Как выделяется площадь в математике

Площадь фигуры

В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.

Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией

Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.

Сравнение площадей фигур

При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.

Например, сравним площади двух фигур: треугольника и круга.

Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.

Сравнение площадей способом наложения

Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:

Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.

Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.

Сравнение площадей заданной меркой

Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:

В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.

Например, меркой может быть вот такой прямоугольник :

В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.

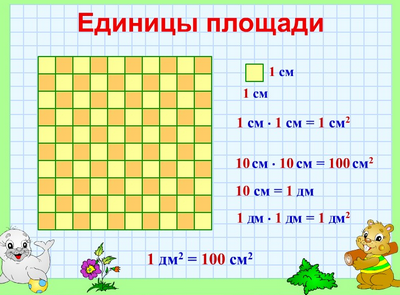
Единицы площади

В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.

Квадратный сантиметр

Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²

Определим площадь данных фигур:

В синей фигуре 8 см², а в красной фигуре – 7 см².

8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.

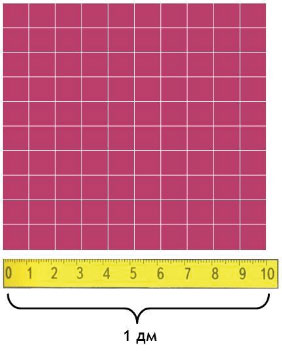
Квадратный дециметр

Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²

Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:

Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть

Значит, 1 дм² = 100 см²

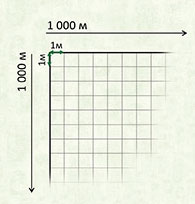
Квадратный метр

Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²

Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.

1 м² = 100 дм²

Квадратный километр

Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²

Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.

1 км² = 1000000 м²

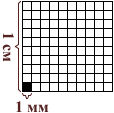
Квадратный миллиметр

Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²

Этой единицей мы пользуемся для измерения очень маленьких площадей.

1 см² = 100 мм²

Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.

Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.

Ар

Слово «ар» при числах сокращённо записывают так:

Гектар

Слово «гектар» при числах сокращённо записывают так:

Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.

Ар и гектар используются при измерении земельных участков.

Поделись с друзьями в социальных сетях:

Источник

Площадь фигур

Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.

Площади равных фигур равны. Их периметры тоже равны.

Площадь квадрата

Для вычисления площади квадрата нужно умножить его длину на саму себя.

S_EKFM = EK · EK

S_EKFM = 3 · 3 = 9 см 2

Формулу площади квадрата, зная определение степени, можно записать следующим образом:

Площадь прямоугольника

Для вычисления площади прямоугольника нужно умножить его длину на ширину.

S_ABCD = AB · BC

S_ABCD = 3 · 7 = 21 см 2

Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.

Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т.д.

Площадь сложных фигур

Площадь всей фигуры равна сумме площадей её частей.

Задача: найти площадь огородного участка.

Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.

Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.

S_ABCE = AB · BC
S_EFKL = 10 · 3 = 30 м 2
S_CDEF = FC · CD
S_CDEF = 7 · 5 = 35 м 2

Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = S_ABCE + S_EFKL
S = 30 + 35 = 65 м 2

Ответ: S = 65 м 2 — площадь огородного участка.

Свойство ниже может вам пригодиться при решении задач на площадь.

Диагональ прямоугольника делит прямоугольник на два равных треугольника.

Площадь любого из этих треугольников равна половине площади прямоугольника.

Вначале найдём площадь прямоугольника по формуле.

S_ABCD = AB · BC
S_ABCD = 5 · 4 = 20 см 2

S _ABC = S_ABCD : 2

S _ABC = 20 : 2 = 10 см 2

S _ABC = S _ACD = 10 см 2

Источник

Площадь (математика, 5 класс) – что такое, правило обозначения и понятие

В школьном курсе математики 4-5 класса рассматривается понятие площади. Это значение часто встречается как в реальной жизни, где мы постоянно интересуемся площадью квартиры, так и при решении задач.

Определение понятия

Площадь указывает на размер плоскости, которую занимает фигура. Если вырезать любую фигуру из листа бумаги, положить на поверхность, а потом обвести карандашом, мы получим визуальное воплощение характеристики площади.

Площади двух абсолютно разных фигур могут быть одинаковыми. Почему так происходит? Потому что площадь – это характеристика. Можно провести простую аналогию с деньгами: сто грамм конфет и полкилограмма крупы стоят одинаково, но это совершенно разные вещи. Так треугольник и прямоугольник могут иметь одинаковую площадь. Фигуры, имеющие одинаковую площадь, называют равновеликими.

Характеристики понятия

Площадь имеет несколько характеристик:

На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.

Площади простых фигур

Формула для определения площади зависит от фигуры. Обозначение площади, чаще всего, остается неизменным – это латинская заглавная буква “S”. Это не правило, просто одна из традиций обозначения площади. В высшей математике, теплотехнике и многих других дисциплинах площадь могут обозначать другими буквами.

Рассмотрим наиболее популярные формулы определения площадей:

Рис. 1. Высота в произвольном треугольнике.

Предварительно нужно убедиться в том, что параметры фигуры находятся в одинаковых единицах измерения. Например, когда ширина прямоугольника представлена в миллиметрах, а длина в сантиметрах, следует перевести сантиметры в миллиметры и только потом использовать формулу.

Рис. 2. Площадь прямоугольника.

Что такое площадь квадрата? Это сторона фигуры, возведенная в квадрат. Потому что квадрат это прямоугольник, длина и ширина которого равны:

Если у квадрата одна сторона равняется 100 м, то его площадь равна одному гектару. Эту единицу используют, когда необходимо оценить размеры земной поверхности при распределении сельскохозяйственных угодий:

Площадь произвольной фигуры

Площадь сложной фигуры можно определить, просуммировав площади ее частей. Для этого нужно просто разделить произвольную геометрическую фигуру на простые составляющие так, чтобы можно было легко определить их квадратуры.

Рис. 3. Площадь сложной фигуры.

Что мы узнали?

Мы познакомились с понятием площади. Узнали, что для каждой фигуры есть свой метод определения площади. Важно, чтобы основные параметры фигуры были выражены в одних и тех же единицах.

Источник

Геометрия

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Понятие площади многоугольника

Понятие площади уже знакомо нам из младших классов и повседневной жизни. Эта величина, которая, грубо говоря, характеризует размер плоских фигур. Она показывает, какую часть плоскости занимает та или иная фигура. Исторически понятие площади многоугольника считалось неопределяемым, так же как понятия точка, прямая, плоскость и т. д. Основная же задача геометров (а именно так называют математиков, специализирующихся на геометрии) сводилась к измерению площади.

Как известно, для проведения любых измерений должна существовать некоторая единица измерения. Так, массу измеряют в килограммах, длину – в метрах и т. д. При этом единицы измерения разных величин могут быть связаны друг с другом. С практической точки зрения удобно принять в качестве единицы измерения площади квадрат, сторона которого равна 1 метру. Принимается, что площадь такого квадрата равна 1 квадратному метру (обозначается символом м 2 ):

Аналогично можно определить такие величины, как квадратный сантиметр (см 2 ), квадратный километр (км 2 ), квадратный миллиметр (мм 2 ) и т.д.:

Как мы знаем, иногда в задачах единицу измерения длины не указывают вовсе. Например, говорят, что сторона квадрата равна единице. В таких случаях и площадь является безразмерной величиной. Принимается, что площадь квадрата со стороной, равной единице, также равна единице. Такой квадрат называется единичным.

Общепринято, что площадь фигуры обозначается буквой S.

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

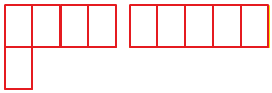
Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут. Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны. Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m 2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R 2 ):

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Соотношение между единицами измерения площадей

Существуют специальные единицы измерения площади, известные как ар (обозначается сокращением а) и гектар (сокращение га). Первый представляет собой квадрат со стороной 10 м, а второй – со стороной 100 м. Верны следующие соотношения:

В частности, если стороны квадратов отличаются в 10 раз, то их площади отличаются уже в 100 раз. Отсюда вытекает быстрый метод перевода единиц площади. Пусть надо перевести 1 квадратный километр в квадратные дециметры. Сначала мы считаем, во сколько раз километр длиннее дециметра:

Решение. Миллиметр в 10 раз меньше сантиметра, а потому 1 см 2 равен 100 мм 2 :

Площадь прямоугольника

Ещё из младшей школы известно, что площадь прямоугольника равна произведению его сторон. Докажем этот факт, используя только свойства площади и выведенную нами ранее формулу площади квадрата.

Возьмем произвольный прямоугольник со сторонами a и b. Далее достроим его до квадрата со стороной (а + b):

Итак, мы доказали следующее утверждение:

Задание. Найдите площадь прямоугольника со сторонами 5 и 8 см?

Решение. Просто перемножаем эти числа:

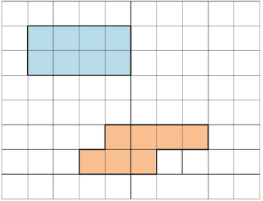
Задание. Найдите площадь фигуры, изображенной на рисунке:

Решение. Необходимо разбить фигуры на несколько прямоугольников:

Далее считаем площадь каждого отдельного прямоугольника:

Задание. Полкомнаты необходимо покрыть паркетом. Длина и ширина комнаты равны 6 и 5,5 метрам, а каждая дощечка паркета имеет габариты 30х5 см. Сколько дощечек паркета необходимо купить для ремонта?

Решение. В таких задачах прежде всего следует все длины выразить в одних единицах измерения. Перепишем габариты комнаты:

Важно убедиться, что пол можно полностью покрыть целым числом дощечек, не используя какие-либо дощечки наполовину. Для этого габариты дощечки должны быть кратны габаритам комнаты. Это условие соблюдается:

Получается, что для покрытия пола дощечки необходимо разместить их в 20 рядов, в каждом из которых будет 110 досок. Тогда общее количество досок будет равно

Задание. Площадь прямоугольника равна 64, а одна из его сторон имеет длину 16. Найдите вторую сторону прямоугольника.

Решение. Запишем формулу площади прямоугольника:

Задание. Найдите стороны прямоугольника, если площадь равна 500, а одна из сторон в 5 раз больше другой стороны.

Решение. Обозначим меньшую сторону переменной х. Тогда большая сторона будет в 5 раз больше, то есть она равна 5х. Площадь прямоугольника будет вычисляться как произведение этих чисел

Мы получили два значения х, 10 и (– 10). Естественно, длина отрезка не может выражаться отрицательным числом, поэтому нам подходит только значение 10. Это длина меньшей стороны. Большая же сторона в 5 раз длиннее, то есть ее длина равна

Решение. Снова обозначим длину меньшей стороны буквой х, тогда большая сторона будет иметь длину х + 5 см. По условию произведение этих сторон равно 150:

Это обычное квадратное уравнение, решаемое с помощью:

Снова получили два корня, из которых только один является положительным. Итак, меньшая сторона равна 10 см. Тогда большая сторона буде равна

Решение. Обозначим смежные стороны буквами a и b. Тогда и две другие стороны также будут равны а и b. Так как периметр (его обозначают буквой Р) по определению является суммой длин всех сторон, то для прямоугольника он будет равен:

Если сюда вместо S подставить 15, а вместо а выражение 8 – b, то получим такое уравнение:

Оба полученных корня являются положительными числами, то есть устраивают нас. Зная b, легко найдем и a:

В первом случае получается, что стороны равны 3 и 5 см. Во втором случае получились те же числа, только в другом порядке: 5 и 3 см. То есть эти два ответа, по сути, идентичны друг другу.

Источник

Математика

Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет

С этой картой можно накопить на мечту, жми ⇒

План урока:

Здравствуйте, друзья! Давайте познакомимся. Я — Сова — Мудрая голова.

Масса моего мозга больше, чем у других птиц. Я, как все учителя, терпелива, замечаю все вокруг, слышу шорохи, обдумываю свои шаги. У многих народов меня считают символом знаний.

Сегодня на уроке мы познакомимся с различными способами сравнения и измерения геометрических фигур, а я поделюсь с вами своей мудростью.

Будь внимателен, дружок!

Понятие площади фигур

Распределите фигуры на группы.

Какие фигуры вы видите?

Прямые и кривые линии, прямые и кривые, овалы, круг, прямоугольники, квадраты, треугольники.

Чем похожи данные фигуры?

Их можно начертить на плоскости.

Чем они отличаются?

Из бумаги можно вырезать только плоские фигуры, у которых кроме длин сторон, можно вычислить и новую величину — площадь.

Для чего это надо нам знать? Когда может пригодиться?

Величины нужны не только для решения математических задач, но и в жизни. Чтобы сделать поделку, надо определить, какое количество бумаги потребуется. При ремонте квартиры мы считаем, сколько купить рулонов обоев, чтобы оклеить стены комнаты. Величина понадобится при постройке дома, при изготовлении какой-либо продукции в промышленности. Даже в саду и огороде хозяйки считают, хватит ли места на грядке.

Как можно объяснить слово площадь? Значение понятий мы узнаем в толковых словарях.

Прочитайте, какой смысл нового термина в словаре С.И. Ожегова.

Как называется главное место столицы нашей страны?

Красная площадь в Москве.

Общую и полезную площадь имеют разные помещения:

Квартира, в которой вы живете.

Классная комната, где вы учитесь.

Спортивный зал, столовая, бассейн школы.

Разные объекты, занимающие место на земле, можно встретить в любом городе.

Интересно, что некоторые люди заводят дома ушастых сов. Но держать птиц в клетке не рекомендуется: для них требуется более просторная комната, где они могли бы летать.

Жилая площадь квартиры

Любым диким животным лучше жить на воле. Сова – это хищная птица. Она питается грызунами, мышами, полевками, насекомыми и птицами. В этом отношении колоссальная польза от совы состоит в том, что за одно лето она может уничтожить около одной тысячи полевых мышей. Каждый грызун уничтожает более килограмма зерна на посевных площадях страны.

Поле с зерновыми культурами

Понятие площади фигуры:

В математике говорят — площадь фигуры. Это величина пространства, ограниченного замкнутым контуром (периметром фигуры).

Ее можно посчитать математическими методами. С этой целью еще в далекой древности была создана целая наука под названием геометрия. Она применялась для деления поля на земельные участки, но потом ее стали использовать для измерения различных фигур. Поэтому их называют геометрическими фигурами, их место на плоскости — площадью.

Сравнение площадей фигур

Мы можем площади плоских фигур сравнить на глазок. Посмотрите на иллюстрацию.

Картина на стене занимает меньше места, потому говорят, что ее площадь меньше, чем стена. Книги, тетради меньше площади крышки стола. Их как бы наложили сверху, и еще осталось место.

Перечислите способы сравнения фигур по площади.

Можно сравнить на глазок или накладывая предметы, фигуры друг на друга.

Расставьте в порядке уменьшения:

Если получилось так: 3, 1, 2, 4, то вы отлично справились.

Теперь сравните треугольник с кругом:

Круг меньше площади треугольника.

Сравнить можно с помощью любых мерок. На рисунке прямоугольники измеряли заданной меркой — треугольником.

В левый прямоугольник их поместилось 18, а в правый — 20. Делаем вывод, что площадь левой фигуры меньше, чем правой.

Хороший способ сравнения — это подсчет клеток.

Чтобы сравнить площади клетчатых фигур, надо пересчитать количество клеток:

Фигура 3 самая маленькая по площади – 6 клеток. Фигура 2 имеют большую площадь, чем 3. В ней 7 клеток. Площади фигур 1,4,5,6 равновеликие. Они равны 8 клеткам, по площади больше фигур 2 и 3.

Разностное сравнение площадей фигур — это нахождение разницы между большей и меньшей величиной.

Сравните площади фигур 3 и 1. Запишите результаты сравнения.

Проверьте себя:

Ответ: 2 клетки

Квадратный сантиметр, дециметр, метр

Какой меркой лучше измерить площадь фигуры квадрата и прямоугольника?

В 18 веке на Руси вводилась основная мера измерения площади — десятина и четь. Но поля крестьян были неровными, поэтому часто мерками служила урожайная копна. Народ изобретал особые мерки: выть, соха, обжа, коробь, веревка, жеребья. Сейчас мы не используем этих мер.

Начертите прямоугольник со сторонами 5см и 4см. Какими мерками можно измерить фигуру?

Посмотрите на рисунок, утенок измерил прямоугольник с помощью треугольников, ежонок — квадратами, а котенок — прямоугольниками.

Посчитаем, сколько единичных мерок находится в прямоугольнике. У животных получились разные величины: 40, 20, 10.

Всегда ли удобно определять площадь фигуры произвольными мерками?

Вывод: значение величины зависит от выбранной мерки. Чтобы сравнить, нужно договориться об одинаковом способе измерения.

Всегда ли для определения площади фигуры подходит клетка?

Какого размера должна быть клетка?

Я предлагаю измерять как ежик, квадратами по 2 клеточки.

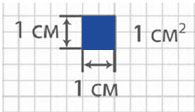
Измерьте длину и ширину этого квадратика. Что получилось?

Длина и ширина равна 1 см.

Единицей измерения площади еще 4-5 тысяч лет тому назад жители древнего города Вавилона считали квадрат, так как именно квадрат имеет превосходные признаки: четыре стороны равны межу собой, четыре прямых угла; можно провести ось и найти центр симметрии. Форма квадрата без изъянов, совершенна, поэтому его легко начертить и плотно покрыть фигуры любой формы.

Если у квадратика сторона 1см – площадь его равна квадратному сантиметру.

1 квадратный сантиметр сравним с ноготком взрослого человека.

Записывается площадь 1 квадратного сантиметра так:

S = 1 кв. см или S = 1 см 2

Латинская буква «эс» обозначает площадь, двойка в правом верхнем углу — две величины: длину и ширину.

Начертите квадрат со стороной 10 сантиметров.

Квадратный дециметр (1 дм 2 ) — это квадрат со стороной 1 дм или 10 см.

Квадратный метр (1 м 2 ) — это квадрат со стороной 1 м или 10 дм. В квадратных метрах обозначается площадь в жилых помещениях, например: в комнатах, коридорах. Эта мерка подойдет для измерения дачного участка, спортивного зала, территории сквера.

А при строительстве школ важно учитывать, сколько квадратных метров должно быть в классе, если для одного ученика по санитарным правилам нужно 4 квадратных метра.

Вы хорошо справляетесь с заданиями. Спине, голове, всему телу нужен отдых. Встаньте на физкультурную минутку.

Физкультминутка

Поднимитесь, вверх потянитесь,

Ниже, ниже тянитесь,

Достаньте мизинцем до пятки.

Получилось? Тогда все в порядке.

Выпрямитесь, грудью вздохните,

Руки шире в стороны разведите.

Соедините в замок на лопатках.

Получилось? Тогда все в порядке.

Глазки зажмурьте, спокойно постойте.

Отдохнули? Теперь посчитайте площадки.

Площадь прямоугольника

Площади простых фигур, таких как квадратов и прямоугольников рассчитывать научились быстро. Для этого измеряют стороны прямоугольника.

Площадь прямоугольника находится по формуле: S = a ∙ b, где длину надо умножить на ширину фигуры.

Задание 1.

Постройте прямоугольник, длина которого 50 мм, а ширина 30 мм.

Можно ли длину и ширину данного прямоугольника выразить в сантиметрах?

Найдите периметр прямоугольника. Р = (a + b) ∙ 2

Ответ: 16 см

Имеет ли построенная вами фигура площадь?

Да. Прямоугольник имеет длину 5 см и ширину 3 см. Найдем, чему равна площадь прямоугольника по формуле S = a ∙ b.

Ответ: площадь прямоугольника равна 15 кв.см.

Задание 2.

Чему равна площадь прямоугольника со сторонами 5 см и 4 см? Рассуждаем так. Нам известна длина и ширина прямоугольника. Площадь равна произведению этих величин.

Ответ: 20 кв.см.

Задание 3.

Рассмотрите следующий рисунок:

Как называется данная геометрическая фигура?

Как найти площадь этого многоугольника?

Найти площади отдельных прямоугольников.

Найдите площадь этого многоугольника разными способами.

Первый способ.

Решение.

Измеряем стороны большого прямоугольника.

Длина равна 3 см, а ширина 3 + 1 = 4 (см).

1) 4 · 3 = 12 (см 2 ) – площадь большого прямоугольника.

Длина маленького прямоугольника 3 см, а ширина 1 см. Перемножим эти величины.

2) 3 · 1 = 3 (см 2 ) – площадь маленького прямоугольника.

Теперь из большей фигуры вырезаем два маленьких белых прямоугольника.

3) S = 12 – 3 – 3 = 6 (см 2 ) – площадь многоугольника.

Второй способ.

Решение.

1) 3 · 1 = 3 (см 2 ) – площадь верхнего прямоугольника.

2) 3 · 1 = 3 (см 2 ) – площадь второго прямоугольника.

3) S = 3 + 3 = 6 (см 2 ) – общая площадь многоугольника.

Ответ: S = 6 см 2

Преобразование величин

По формуле S = a ∙ b квадратные сантиметры можно выразить в квадратных метрах. Давайте вспомним, что один метр равен сто сантиметрам.

Мы выполним умножение сторон, и найдем квадратную величину.

Значит: 1 м 2 = 100 ∙ 100 = 10000 см 2

Задание 4.

1 м 2 = 10 ∙ 10 = 100 дм 2

Ответ: в 1 кв. м содержится 100 кв.дм. 1 кв.м. в сто раз больше одного квадратного дециметра.

Задание 5.

Сколько кв. см в 1 кв. дм? Во сколько раз 1 кв. дм. больше 1 кв. см?

Выражаем квадратные дециметры в квадратных сантиметрах.

1 дм 2 = 10 ∙ 10 = 100 см 2

Ответ: 1 кв.дм равен 100 кв.см. 1 кв.дм в сто раз больше одного квадратного сантиметра.

Выполните упражнение:

Наш урок подходит к концу.

Продолжите фразу:

сегодня я научился

Вы хорошо потрудились, поэтому сможете справиться с самостоятельными заданиями.

Источник