Как выглядит 6 угольник картинка
Правильный шестиугольник и его свойства

Определение и построение
Правильным шестиугольником называется плоскостная фигура, имеющая шесть равных по длине сторон и столько же равных углов.
Если вспомнить формулу суммы углов многоугольника
то получается, что в этой фигуре она равна 720°. Ну а поскольку все углы фигуры равны, нетрудно посчитать, что каждый из них равен 120°.
Начертить шестиугольник очень просто, для этого достаточно циркуля и линейки.
Пошаговая инструкция будет выглядеть так:
При желании можно обойтись и без линии, начертив пять равных по радиусу окружностей.
Полученная таким образом фигура будет правильным шестиугольником, и это можно доказать ниже.
Свойства простые и интересные
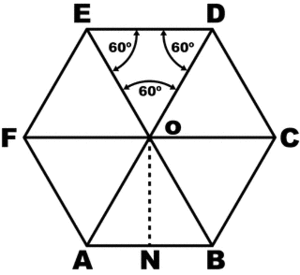
Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:
Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:
Описанная окружность и возможность построения
Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.
После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:
Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.
Ну а площадь этой окружности будет стандартная:
Вписанная окружность
Высота равностороннего треугольника вычисляется просто:
h²=а²-(а/2)²= а²3/4, h=а(√3)/2
А поскольку R=a и r=h, то получается, что
r=R(√3)/2.
Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.
Ее площадь будет составлять:
S=3πa²/4,
то есть три четверти от описанной.
Периметр и площадь
С периметром все ясно, это сумма длин сторон:
P=6а, или P=6R
А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:
S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или
S=3R²(√3)/2
Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:
Занимательные построения
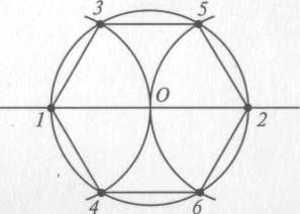
В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:
Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:
Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:
Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:
d=а(√3)/3
Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:
Площадь нового шестиугольника можно посчитать так:
Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.
От теории к практике
Нашла свое применение и гексагональная плитка. Она распространена куда меньше четырехугольной, но класть ее удобнее: в одной точке смыкаются три плитки, а не четыре. Композиции могут получаться очень интересные:
Выпускается и бетонная плитка для мощения.
Распространенность гексагона в природе объясняется просто. Таким образом, проще всего плотно уместить круги и шары на плоскости, если у них одинаковый диаметр. Из-за этого у пчелиных сот такая форма.
Шестиугольник, виды, свойства и формулы
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
2. Все углы равны между собой и составляют 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
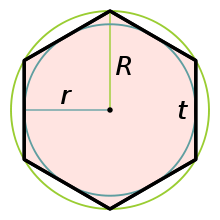
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Столбы базальтов от извержения старого вулкана. Снежинка. Пчелиные ульи. Кораллы, кристаллы и множество других структур, как биологических, так и небиологических, имеют форму шестиугольника. Почему природа, которая часто кажется такой беспорядочной и неправильной, предпочитает именно эту форму? Оказывается, все дело в геометрии и физике.
Соты строятся из пчелиного воска, вырабатываемого рабочими пчелами. Они вырабатывают воск из специальных желез в своем теле, которые затем смешивают с небольшим количеством меда и пыльцы, которую они разжевывают, чтобы получить пчелиный воск. Соты будут служить сосудами для хранения меда, а также камерами для выращивания молодых пчел.
Все это хорошо и замечательно, но почему шестиугольники?
Вымерший коралл Cyathophyllum hexagonum даже назван в честь своей шестиугольной формы, а некоторые диатомовые водоросли (основная группа водорослей) также имеют шестиугольную форму. Но, пожалуй, ни одна биологическая структура не имеет такой поразительной шестиугольной формы, как глаза стрекоз.
Глаза, состоящие примерно из 30 000 шестиугольников, переплетенных в ослепительное множество, являются одними из лучших в животном мире. Фактически, глаза стрекоз состоят из правильных шестиугольников, причем только три из этих шестиугольников встречаются в любой данной точке пересечения (или вершине).
У стрекоз два больших сложных глаза с тысячами шестиугольных линз (а также три глаза с простыми линзами, но оставим их пока в стороне). Шестиугольные линзы соединены между собой длинным тонким сетчатым каналом. На самом деле, у многих насекомых глаза имеют шестиугольную форму, и правило всегда гласит, что только три стенки клетки могут встречаться в любой вершине.
На самом деле, если мы на мгновение отойдем от биологического мира, то обнаружим, что точно такое же правило управляет чем-то совершенно другим: пеной из пузырьков.
Хотя пена пузырьков остается трудноразрешимой математической задачей, известно, что пена часто имеет тенденцию образовывать шестиугольные формы. В данном случае речь идет о поиске структуры с наименьшим общим поверхностным натяжением (что означает наименьшую площадь стены из мыльной пленки), и эта форма оказывается шестиугольником.
Конечно, структуры пены редко бывают идеально шестиугольными (а иногда они вообще не шестиугольные), потому что они также должны быть механически устойчивыми (и противостоять таким вещам, как ветер). Что еще более усложняет ситуацию, трехмерное расположение делает проблему еще более сложной. Несмотря на склонность к шестиугольникам, пена редко бывает упорядоченной.
На самом деле было удивительно много споров о том, какие формы может принимать пена, исследователи предлагали трехмерные 14-гранные многогранники и даже некоторые более безумные и беспорядочные формы. Но именно здесь становится интересно. Правила, управляющие формой ячеек в пене, похоже, также управляют некоторыми формами живых клеток. Дело не только в том, что глаза некоторых мух имеют такие же шестиугольные узоры, как и пена пузырьков, но и в том, что клетки внутри отдельных линз сгруппированы таким образом, что, похоже, повторяют геометрию пены пузырьков. Это поразительный случай, когда физика и математика направляют формы в биологическом мире.
Соединение колонн в Дороге гигантов в Северной Ирландии.
Но не вся лава остывает в одно и то же время, и некоторые участки могут все еще течь, в то время как другие уже затвердели, что может сделать формы более несовершенными. Поразительно, что часто угол удивительно близок к 120 градусам.
Если вы все еще не верите в существование шестиугольников в природе, вот еще один пример: снежинки.
Конечно, каждая снежинка уникальна, но все снежинки имеют шесть сторон или точек, и это связано с тем, как они формируются. Внешняя форма снежинок отражает их внутреннюю структуру. Гексагональная структура позволяет молекулам воды (с одним атомом кислорода и двумя атомами водорода) группироваться вместе наиболее эффективным образом.
Можете ли вы заметить шестиугольную структуру в этой снежинке?
Если мы еще больше увеличим масштаб, то обнаружим еще одну форму шестиугольника. Как быстро отметит любой студент-химик, шестиугольники являются основой органической химии. Когда шесть атомов углерода соединяются, угол составляет 120 градусов, что уже должно быть знакомо. Шесть соединенных атомов углерода образуют идеальный шестиугольник, который также называется бензольным кольцом.
Есть еще один пример, который мы должны рассмотреть, и мы перейдем от очень маленьких к очень большим. Планета Сатурн имеет один из самых необычных шестиугольников в Солнечной системе: облачный узор длиной около 14 500 км; он больше, чем весь диаметр Земли. Шестиугольник состоит из газов, движущихся со скоростью 320 км/ч, и, как полагают, имеет толщину до 300 км.
Исследователи точно не знают, почему так происходит, но уже выдвинуто несколько теорий.
Почему же шестиугольники так часто встречаются в природе? Это зависит от того, как на это посмотреть. Это может быть эффективный способ сохранения массы или энергии, или просто способ расположить атомы таким образом, чтобы они были стабильны. Это может быть просто что-то, обусловленное геометрией.
Шестиугольник
Шестиугольник — многоугольник с шестью углами. Также шестиугольником называют всякий предмет такой формы.
Сумма внутренних углов выпуклого шестиугольника равна 720°.
Правильный шестиугольник
Правильным называется шестиугольник, у которого все стороны и углы равны.
См. также
Планигон
Полезное
Смотреть что такое «Шестиугольник» в других словарях:
шестиугольник — гексагон Словарь русских синонимов. шестиугольник сущ., кол во синонимов: 3 • гекзагон (1) • … Словарь синонимов
ШЕСТИУГОЛЬНИК — ШЕСТИУГОЛЬНИК, плоская фигура, имеюшая шесть сторон, сумма внутренних углов которой равна 720°. У обычного шестиугольника все стороны и углы равны, и каждый угол равен 120° … Научно-технический энциклопедический словарь
ШЕСТИУГОЛЬНИК — ШЕСТИУГОЛЬНИК, шестиугольника, муж. (мат.). Многоугольник с шестью углами. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
шестиугольник — (6 угольник) … Орфографический словарь-справочник
шестиугольник — šešiakampis statusas T sritis fizika atitikmenys: angl. hexagon vok. Sechseck, n rus. шестиугольник, m pranc. hexagone, m … Fizikos terminų žodynas
Шестиугольник — м. 1. Геометрическая фигура, ограниченная замкнутой ломаной линией, образующей шесть внутренних углов. 2. Пространство или предмет такой формы. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
шестиугольник — шестиугольник, шестиугольники, шестиугольника, шестиугольников, шестиугольнику, шестиугольникам, шестиугольник, шестиугольники, шестиугольником, шестиугольниками, шестиугольнике, шестиугольниках (Источник: «Полная акцентуированная парадигма по А … Формы слов
шестиугольник — шестиуг ольник, а … Русский орфографический словарь
шестиугольник — (2 м); мн. шестиуго/льники, Р. шестиуго/льников … Орфографический словарь русского языка
шестиугольник — шестиуго/льник, а (6 уго/льник) … Слитно. Раздельно. Через дефис.
Пчелиная экономия: почему природа предпочитает шестиугольники?
Ксения Донская
При достаточной наблюдательности в живой природе легко обнаружить строгую геометрию. В особом почете оказываются гексагоны — правильные шестиугольники. Почему их так любят пчелы и архитекторы и какие у них преимущества с точки зрения физики, рассказал английский ученый и научный журналист Филип Болл. «Теории и практики» перевели отрывок из книги «Закономерности в природе: Почему живой мир выглядит так, как выглядит», опубликованный на сайте Nautilus.
Как пчелам это удается? Соты, в которых они хранят золотистый нектар, — это чудеса инженерного искусства, набор ячеек в форме призмы с правильным шестиугольником в основании. Толщина восковых стенок строго определена, ячейки немного отклоняются от горизонтали, чтобы вязкий мед не вытекал, и соты находятся в равновесии с учетом влияния магнитного поля Земли. А ведь эту конструкцию без чертежей и прогнозов строят множество пчел, которые одновременно работают и координируют свои попытки сделать соты одинаковыми.
Древнегреческий философ Папп Александрийский думал, что пчелы, должно быть, наделены «геометрическим предвидением». И кто, если не Господь, мог одарить их такой мудростью? Как писал английский энтомолог Уильям Керби в середине XIX века, пчелы — «математики от Бога». Чарльз Дарвин не был в этом уверен и проводил эксперименты, чтобы установить, могут ли пчелы строить идеальные соты, используя лишь приобретенные и врожденные способности, как предполагалось в его теории эволюции. Но все же почему шестиугольник? Это чисто геометрический вопрос. Если вы хотите сложить вместе несколько одинаковых по форме и размерам ячеек таким образом, чтобы они заполняли всю плоскость, подойдут только три правильные фигуры (с равными сторонами и углами): равносторонние треугольники, квадраты и гексагоны. Если выбирать из этих вариантов, то шестиугольные соты потребуют наименьшей общей длины перегородок, в отличие от треугольников и квадратов той же площади. Поэтому в пчелиной любви к гексагонам есть смысл: на изготовление воска тратится энергия, и они стараются минимизировать расходы — точно так же, как строители пытаются сэкономить на стоимости кирпичей. К такому выводу пришли в XVIII веке, и Дарвин объявил, что соты из правильных шестиугольников «идеальны для экономии труда и воска».
Дарвин думал, что естественный отбор наделил пчел инстинктами для строительства восковых ячеек, у которых есть весомое преимущество: на них нужно тратить меньше времени и энергии, чем на соты других форм. И хотя кажется, что пчелы действительно обладают особыми способностями в том, что касается измерения углов и толщины стен, мнения ученых по поводу того, насколько активно насекомые их используют, расходятся, поскольку скопления шестиугольников встречаются в природе довольно часто.
Если вы подуете на пузырьки на поверхности воды, чтобы согнать их вместе, то они приобретут форму шестиугольников — или, по крайней мере, приблизятся к ней. Вы никогда не увидите скопище квадратных пузырей: если даже четыре стенки соприкоснутся, они немедленно перестроятся в конструкцию с тремя сторонами, между которыми будут примерно равные углы в 120 градусов — что-то вроде центра эмблемы «Мерседеса».
Очевидно, нет никаких организмов, которые работали бы над этими склеенными пузырями, как пчелы над сотами. Рисунок образуется исключительно благодаря законам физики. Так же очевидно, что у этих законов есть определенные предпочтения: например, склонность к трехстороннему соединению стенок пузырей. Аналогичная вещь происходит и с пеной, которая сложнее по строению. Если вы дуете через соломинку в мыльную воду и создаете «гору» пузырей в трехмерном пространстве, вы видите, что их стенки при соприкосновении всегда создают четырехсторонний союз и пересекающиеся мембраны находятся под углом около 109 градусов — это угол, который имеет непосредственное отношение к тетраэдру.
Что определяет форму пузырей и закономерности образования «развилок» мыльных стенок? Природа еще более озабочена экономией, чем пчелы. Пузыри и мыльная пленка состоят из воды (и слоя мыльных молекул), и поверхностное натяжение сжимает поверхность жидкости таким образом, чтобы она занимала наименьшую площадь. Поэтому капли дождя при падении принимают форму, близкую к сферической: у сферы наименьшая площадь поверхности по сравнению с другими фигурами того же объема. На восковом листке капли воды сжимаются в маленькие бусинки по той же причине.
Поверхностное натяжение объясняет и тот узор, который образуют пузыри или пена. Пена стремится к такой конструкции, при которой общее поверхностное натяжение будет минимальным, а значит, минимальной должна быть и площадь мыльной мембраны. Но конфигурация стенок пузырей должна быть прочной и с точки зрения механики: натяжение в разных направлениях на «перекрестке» должно быть идеально сбалансировано (по тому же принципу нужен баланс при строительстве стен собора). Трехстороннее соединение в пленке из пузырьков и четырехстороннее — в пене — комбинации, которые достигают этого баланса.
Но тем, кто думает (а такие имеются), что соты — это просто застывшее обилие пузырей из теплого воска, трудно будет объяснить, как такие же множества шестиугольных ячеек получаются у бумажных ос, которые при строительстве используют не воск, а комки жеваных волокон древесины и стеблей, из которых они изготавливают подобие бумаги. Мало того, что поверхностное натяжение тут не играет особой роли, но к тому же ясно, что у разных видов ос разные врожденные инстинкты с точки зрения архитектурных решений: они могут значительно различаться.
Хотя геометрия стыков стенок пузырей диктуется взаимодействием механических сил, в ней бессмысленно искать намек на то, какую форму должна принять пена. Обычная пена содержит многогранные элементы различной формы и размера. Присмотритесь — и вы увидите, что их стенки не идеально прямые: они немного изогнуты. Поскольку чем меньше пузырь, тем выше в нем давление газа, стенка маленького пузыря рядом с большим будет слегка выпирать вперед. Более того, у некоторых элементов пять граней, у других — шесть, а у только четыре или всего три. При небольшой гибкости стенок все эти формы могут образовать четырехстороннее соединение, близкое по композиции к тетраэдру, что необходимо для механической устойчивости. Так что форма пузырей может изменяться. И хотя пену можно изучать с помощью правил геометрии, по своей сути она довольно хаотична.
Предположим, что вы могли бы сделать «идеальную» пену, в которой все пузыри одного размера. Какой тогда должна быть их идеальная форма, чтобы общая площадь стенок была наименьшей, но требование для углов на стыке выполнялось? Этот вопрос обсуждался много лет, и долгое время считалось, что идеальной формой будет четырнадцатигранник c квадратными и шестиугольными гранями. Но в 1993 году была открыта немного более экономичная, хотя и менее упорядоченная структура, состоящая из повторяющейся группы из восьми разных форм. Этот более сложный рисунок был использован в качестве вдохновения для пеноподобного дизайна водного стадиона для Олимпиады 2008 года в Пекине.
Здание Национального плавательного комплекса в Пекине © Ben McMillan
Правила, работающие для пузырей в пене, также можно отнести и к другим узорам, которые обнаруживаются в живых организмах. Не только фасеточные глаза мухи состоят из групп шестиугольных ячеек, которые напоминают группы пузырей; еще и светочувствительные клетки в каждой из этих ячеек собираются в гроздья по четыре, что опять же напоминает мыльные пузыри. Даже в случае мух-мутантов, у которых таких клеток больше, можно говорить о том, что их организация более-менее идентична поведению пузырей.
Из-за поверхностного натяжения мыльная пленка, охватывающая проволочную петлю, натянута ровно, как упругая сетка батута. Но если проволочный каркас погнут, то пленка также будет выгибаться элегантным контуром, который автоматически подсказывает вам наиболее экономичный с точки зрения использования материала способ покрытия пространства, огороженного каркасом. Таким образом, архитектор может увидеть, как построить крышу для здания со сложной архитектурой и потратить минимум стройматериалов. Как бы то ни было, дело не только в экономичности этих так называемых минимальных поверхностей, но и в их красоте и элегантности; вот почему такие архитекторы, как Фрай Отто, использовали их в качестве вдохновения для своих работ.
Эти поверхности минимизируют не только площадь, но и кривизну. Чем круче изгиб, тем больше кривизна. Она может быть положительной (выпуклости) или отрицательной (углубление, впадина или прогиб). Средняя кривизна изогнутой поверхности будет нулевой, если положительная и отрицательная кривизна друг друга уравновешивают. Поэтому лист может быть весь покрыт искривлениями, а средняя кривизна окажется наименьшей. Такая минимально искривленная поверхность разрезает пространство аккуратным лабиринтом коридоров и каналов — сетью.
Фрай Отто, Олимпийский стадион в Мюнхене © Atelier Frei Otto Warmbronn
Это явление называют периодической минимальной поверхностью («периодическая» лишь означает, что эта структура повторяется вновь и вновь; другими словами, это постоянная последовательность). Когда такие последовательности были обнаружены в XIX веке, они казались просто математическим курьезом. Но теперь мы знаем, что природа извлекает из них пользу.
Клетки организмов различных видов, от растений до миног или крыс, обладают мембранами с подобными микроскопическими структурами. Никто не знает, зачем они нужны, но они встречаются настолько часто, что логично предположить, что они выполняют какую-то полезную функцию. Может быть, они отделяют один биохимический процесс от другого, упраздняя их взаимное влияние друг на друга. Или, возможно, они просто эффективны в качестве «рабочей поверхности», поскольку многие биохимические процессы протекают на мембранах, где могут находиться ферменты и другие активные молекулы. Каковы бы ни были функции таких лабиринтов, вам не понадобятся сложные генетические инструкции для их строительства: законы физики сделают все за вас.
У некоторых бабочек, таких как голубянка малинная, на крыльях есть чешуйки, в которых располагается аккуратный лабиринт из жесткого материала — хитина, — сформированный в виде определенной периодической минимальной поверхности под названием гироид. Взаимодействие между неровностями на чешуйчатой поверхности крыльев приводит к тому, что волны определенной длины — то есть определенные цвета — исчезают, в то время как другие усиливают друг друга. Этот механизм влияет на окраску насекомого.
Скелет морского ежа Cidaris rugosa — пористая совокупность ячеек в форме другого вида периодической минимальной поверхности. Это экзоскелет, который расположен снаружи мягких тканей организма, защитная раковина, на которой растут кажущиеся опасными колючки из того же минерала, который входит в состав мела и мрамора. Открытая решетчатая структура указывает на то, что материал прочный, но при этом нетяжелый, — как пенометалл, который используется в авиастроительстве.
Чтобы создать упорядоченную конструкцию из твердого неподатливого минерала, эти организмы, по всей видимости, делают макет из мягкой гнущейся мембраны и затем кристаллизуют твердое вещество внутри одной из взаимопроникающих сетей. Другие существа могут использовать минеральную пену для более сложных задач. Из нее они выстраивают конструкции-«трельяжи», которые, как зеркала, могут направлять свет за счет особенностей его отражения от рельефа. Сеть полых микроскопических каналов, напоминающих соты, в хитиновых щетинках необыкновенного морского червя (морской мыши) превращает эти волосоподобные структуры в природное оптическое волокно, которое может преломлять свет, благодаря чему цвет существа может измениться от красного до в зависимости от направления освещения. Изменение окраски помогает отпугивать хищников.
Этот принцип использования мягких тканей и мембран в качестве макета для формирования упорядоченного минерального экзоскелета широко распространен среди морских обитателей. Некоторые морские губки имеют экзоскелеты, сделанные из минеральных стержней, соединенных по принципу «паутинки» на детских площадках, и они невероятно напоминают формы, которые складываются при столкновении мыльных пузырей в пене, — и тут не может быть никаких разговоров о совпадениях, поскольку архитектуру диктует поверхностное натяжение.
Подобные процессы, известные как биоминерализация, дают впечатляющий результат в таких морских организмах, как лучевики и диатомеи. У некоторых из них встречаются аккуратно выстроенные экзоскелеты, состоящие из минеральных ячеек в виде гексагонов и пентагонов: их можно назвать морскими сотами. Когда немецкий естествоиспытатель (и талантливый художник) Эрнст Геккель впервые увидел эти формы в микроскоп в конце XIX века, он сделал их главным украшением своего собрания рисунков под названием «Красота форм в природе», которое сильно повлияло на художников начала XX века и до сих пор вызывает восхищение. Для Геккеля эти конструкции были доказательством фундаментальной креативности природы — предпочтение порядка и узоров, встроенное в сами законы естества. Даже если сегодня мы не разделяем эту теорию, что-то есть в этой убежденности Геккеля в том, что упорядоченность — это неудержимый импульс живого мира, и мы по праву можем считать его прекрасным.