Как выглядит координатный луч в математике
Шкалы. Координатный луч
Содержание
Для измерения длины отрезка используется линейка. Измерение возможно за счет того, что на линейку нанесена шкала — это штрихи через одинаковые промежутки.
На школьный линейках, как правило, расстояние между штрихами равно 1 мм, оно называется делением.
Дополнительно на линейках обозначены и сантиметровые интервалы — под удлиненными штрихами стоят цифры. Один сантиметровый отрезок содержит в себе 10 делений по 1 мм.
Шкалу также можно увидеть в термометре. Там одно деление соответствует одному градусу, цифрами обозначены величины, равные 10, 20, 30 градусам и т.д.
Еще шкала бывает на весах. Обычно одно деление весов равно 100 гр. Цифрами обозначены величины в 1, 2, 3 кг и т. д.
Но если нужно взвешивать большие предметы, то применяются весы, деление шкалы в которых больше чем 100 гр. В этом случае используются такие единицы измерения массы, как тонна и центнер.
1 тонна обозначается как 1 т, 1 т = 1000 кг.
1 центнер обозначается как 1 ц, 1 ц = 100 кг.
Шкала также есть на таком приборе, как динамометр
Координатный луч
В математике шкалу можно встретить на координатном луче. Разберем подробнее, что это за луч и как его построить.
Начертим луч ОХ, как показано на рисунке 1.
Рисунок 1
Точка О является его началом. Она соответствует числу 0. От точки О вправо отложим отрезок, равный 1 см, а полученную точку обозначим Е (рисунок 2).
Рисунок 2
Точка Е будет соответствовать числу 1. Отрезок ОЕ называется единичным.
Таким образом, луч ОХ стал координатным лучом, где О — это начало координат, а ОЕ — единичный отрезок. (Единичный отрезок в нашем примере равен 1 см, но он может быть любой длины, именно это длина будет приниматься на координатном луче за единицу измерения.)
Числа, соответствующие точкам на координатном луче, называются координатами этих точек. Говорят так: точка О имеет координату 0, точка Е имеет координату 1. Записывается это следующим образом: О(0), Е(1).
Рисунок 3
Отметим на координатной луче точки А(2), В(3), С(4) — рисунок 3. Так мы получили на координатном луче шкалу, которую можно продолжать бесконечно.
5.4.4. Изображение чисел на координатном луче
Примеры.
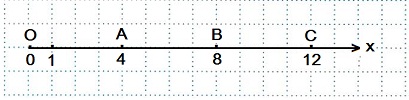
1) Отметить на координатном луче точки А(4), В(8), С(12).
Выбираем единичный отрезок — одну клетку.
Читают: точка А с координатой 4. Точка В с координатой 8. Точка С с координатой 12.
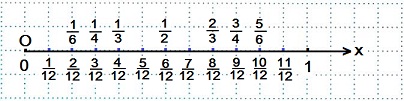
2) Изобразить на координатном луче все правильные дроби со знаменателем, равным 12.
Выбираем единичный отрезок — 12 клеток. Тогда одна клетка будет равна одной двенадцатой доли единичного отрезка, равного 12 клеткам.
Любому числу координатного луча соответствует единственная точка. И если под и над точкой стоят два числа, то это означает, что эти два числа равны между собой (смотрите тему: «Сокращение обыкновенных дробей»).
3) Начертить координатный луч, выбрать единичный отрезок, равный 6 клеткам и отметить точки: А( 1/6), В(2/3), С(1½), D (2 1 /3).
За единичный отрезок мы взяли 6 клеток.
Число 1½ означает, что ½ единичного отрезка (3 клетки) следует откладывать не от нуля, а от 1 целой.
Число 2 1 /3 изображаем так: отсчитываем 2 целые единицы (2·6=12 клеток) и еще 2 клетки.
4) На координатном луче отметить точки: А(5/8), В(1¾), С(2½).
Презентация по математике на тему «Координатный (числовой) луч».(5 класс)
Описание презентации по отдельным слайдам:
От начала луча будем откладывать один за другим равные отрезки.
У начала луча, точки А, поставим число нуль и перенумеруем один за другим концы отрезков.
Началу числового луча соответствует число 0. На числовом луче любое число можно изобразить точкой, каким бы большим оно не было
С помощью числового луча легко сравнивать: чем правее точка от начала луча, тем большее число она изображает.
С помощью числового луча назови все числа, которые меньше числа 8, и те числа, которые больше, чем 8.
Запиши, каким числам на числовом луче соответствуют точки А, В, С, К.
Координатный луч Чтобы начертить координатный луч необходимо: отметить точку О – начало луча на пересечении клеток; провести луч так, чтобы он шел слева направо О Точка О имеет координату 0 0 Координатный луч не построен, если нет единичного отрезка. Чтобы построить единичный отрезок: отметим спава на луче точку А дадим точке А координату 1 А 1 Расстояние от точки О до точки А, т.е. расстояние от 0 до 1 и есть единичный отрезок.
Единичный отрезок Единичный отрезок может иметь разную длину Например, нам надо построить координатный луч с единичным отрезком равным две клетки О Для этого необходимо: построить луч (по правилам, которые рассматривались выше) отсчитать от точки О две клетки отметить точку и дать ей координату 1 расстояние от 0 до 1, равное двум клеткам и есть единичный отрезок 0 1 Ниже координатный луч с единичным отрезком равным пяти клеткам О 0 1
Координаты В качестве примера координатного луча можно взять обыкновенную линейку. единичный отрезок Пусть дан координатный луч, единичный отрезок которого равен 3 клетки. О 0 1 Чтобы отметить точку В надо: от точки О отложить три отрезка, один за другим. эти отрезки должны быть одинаковой длины и равны единичному отрезку. в конце третьего отрезка отметить точку В и дать ей координату 3 3 В Единичный отрезок у линейки равен 1 см Отметим на нем точку В с координатой 3. 4 5
Задание 1 а)Начертите координатный луч с единичным отрезком, равным 4 клеткам Отметьте на данном луче точки: А (2), С (1), L (5) 5 1 2 3 б)Начертите координатный луч с единичным отрезком, равным 7 клеткам Отметьте на данном луче точки: А (2), С (1), D (5)
Задание 2 О 0 1 В С Р Дан координатный луч Напишите чему равен его единичный отрезок Напишите координаты точек: О В С Р Чтобы записать чему равна координата точки надо: написать букву, которой обозначена точка в скобка записать число соответствующее координате Например: точка А имеет координату 1 запишется как А(1) 4 1 2 3
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Данная презентация предназначена для учащихся 5 классов. Работа состоит из 12 слайдов. В ходе урока по данной теме ученики знакомятся с понятием координатного (числового) луча. Учащиеся изучают пошаговый алгоритм построения координатного луча,изучают понятие единичного отрезка,понятие координаты точки. Дается правило сравнения чисел с помощью координатного луча. После теоретического материала следуют задания на закрепление: учащимся предлагается построить координатный луч с различными значениями единичных отрезков; по данному рисунку уметь определять координаты точек.
Номер материала: 478985
Не нашли то что искали?
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Большинство родителей в России удовлетворены качеством образования в детсадах
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%
Время чтения: 2 минуты
Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах
Время чтения: 0 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Что такое луч в математике (5 класс)
Всего получено оценок: 339.
Всего получено оценок: 339.
Луч – это одно из основных базовых построений наравне с точкой и прямой. Изучение луча в курсе математики 5 класса дает начало другим важным темам: системам координат и углам на плоскости.
Определение
Луч это прямая, ограниченная с одной стороны. Это определение лучше усвоится, если выучить свойства луча:
Правильное обозначение луча спорный вопрос. Наиболее правильный вариант это две точки, например ОА. Причем первой точкой обозначают начало луча. Но также обозначают отрезки и прямые, поэтому чаще пишут луч с началом в точке О.
Углы – это единственные фигуры, состоящие из лучей. Что такое угол? Это геометрическая фигура, состоящая из двух лучей, начало которых лежит в одной точке. В фигурах углы состоят из отрезков, а не из лучей.
Может случиться ситуация, когда оде стороны угла будут совпадать, тогда говорят, что величина угла равна 0 градусов. Может получиться и так, что обе стороны угла образуют прямую, тогда говорят, что угол равен 180 градусам. Такой угол называют развернутым, а лучи основным и дополнительным.
Величина угла отражает поворот одного луча относительно другого.
Координатные лучи
Еще одно применение лучей это различные системы координат. В математике 5 класса первой темой идет изучение координатной прямой. Это два луча с углом поворота в 180 градусов. Начало лучей обозначается за нулевую точку или начало отчета. Влево от начала отчета откладываются отрицательные координаты, в право-положительные. Другое название координатной прямой: числовой луч.
Рис. 2. Координатный луч.
С помощью координатного луча удобно сравнивать дроби и таким образом решать неравенство.
С помощью координатных лучей создается и координатная плоскость. Так называемая декартова система координат состоит из двух координатных прямых или 4 лучей. Подобная система позволяет определять положение точки на плоскости, вычерчивать графики функций и графически решать разного рода уравнения.
Помимо декартовой системы существует полярная система координат. В полярной системе используются понятия угла и координатной прямой. Координатная прямая определяет положение точки, а угол степень ее подъема над осью.
Полярная система координат одна из самых древних в истории человечества. Так сложилось, что именно пользуясь этой системой, древние мореплаватели покоряли неизвестные просторы нашего мира. Декартова система появилась гораздо позднее. Но она более удобна для ориентации на местности. Декартову систему проще использовать как в разделах математики, так и других дисциплинах: физике, теплотехнике, гидравлике и программировании.
Декартовая система четырьмя лучами делиться на 4 четверти, положение точки в каждой из которых определяется знаком координат. Координаты подразделяют на абсциссы и ординаты. Проще говоря на х и у. Например точка (3, 4) имеет две положительные координаты, а значит она будет находиться в первой четверти. Обе отрицательные координаты соответствуют третьей четверти, положительный у при отрицательном х это вторая четверть, а отрицательный у при положительном х – четвертая.
Чтобы построить точку в декартовых системах координат необходимо от деления числового луча, соответствующего координате, поднять перпендикуляр. Координаты две, значит и перпендикуляров будет два. Точка их пересечения и будет искомой точкой.
Числовая прямая
Числовая прямая – это луч, с нанесенными на него числами или интервалами чисел. Числовую прямую используют для сравнения дробей, рисунков к задаче и нахождения ОДЗ функции. Последнее встречается чаще всего.
Фигурной скобкой на прямой обозначается область, в которую не могут попадать корни. После решения уравнения, найденные корни наносятся на числовую прямую. Попавшие в фигурную скобку недопустимых значений корни исключаются из решения.
Рис. 3. Числовая прямая.
Что мы узнали?
Мы узнали, что такое луч и числовая прямая. Поговорили о фигурах, составленных из лучей и системах координат, где применяются числовые прямые. Проработали вопрос наглядности изображения нужных точек и разобрались с тем, как правильно проставлять координаты на координатном луче.
Координатный луч
Прямая линия бесконечна в оба конца. И на ней очень удобно изображать числа. Давай разберемся как это делать.
Начертим на листе бумаги в клетку прямую линию.
Отметим на ней точку, которую назовем начальной и обозначим буквой О.
Эта точка разделит нашу прямую на две части. Такие две части прямой называются лучами. И они тоже бесконечны, как и прямая. Один идет до бесконечности вправо, другой до бесконечности влево. Мы с тобой будем сейчас работать только с тем лучом, который идет вправо.
На нем располагаются положительные числа, то есть числа больше нуля (есть еще и отрицательные, но о них мы будем говорить немного позже, поэтому луч на котором отрицательные числа расположены, мы сделаем невидимым).
И начнем работать с правым лучом.
Теперь отступим от точки О вправо на одну клетку, поставим точку и напишем под ней 1 (ведь мы сделали только один шаг).
Потом отступим еще на одну клетку, опять поставим точку и напишем цифру 2 (теперь мы сделали два шага) и так далее. Конечно же, мы не можем написать все числа, которые можно уместить на координатном луче, ведь он бесконечен, значит, и количество шагов, которое мы можем сделать, тоже бесконечно. Но мы можем написать их столько, сколько их поместиться на тетрадном листе (пишем постепенно, то есть делаем шаг и под новой точкой записываем, сколько же шагов мы уже сделали).
Дальше я буду писать букву O красным. То есть красным будем писать название буквы O, а синим под ней количество шагов, то есть ноль. Можно было бы выбрать другую букву, так как O похожа на ноль, но для того, чтобы обозначить начало отсчета шагов по лучу чаще всего во всех учебниках используют именно букву О, поэтому давай будем придерживаться общего правила. Эту точку также называют «начало координат».
Получается, что у каждой точки на луче есть свой номер, свой адрес? Да. Это количество шагов, которое мы сделали по лучу вправо, чтобы достичь этой точки. Это количество шагов называется координатой точки. А сам луч именно потому и называется координатным, потому что на нём записаны координаты точек. Еще раз повторим – буквы (большие латинские, например, A,B,C,F,G, H и другие) – это имена (названия) точек. А цифры под ними – это координаты точек. Не путай. Обычно точку записывают так: сначала пишут ее имя (название), а потом в скобках указывают координату. Посмотри на рисунок. Давай запишем, какие точки у нас изображены.
И наоборот. Предположим, нам написали точки с координатами и просят их отметить на координатном луче. Например, F(4), E(7), G(12)
Чертим луч с точкой О в начале (это начало отсчета или начало координат).
Выбираем единичный отрезок. Пусть он будет 2 клетки. И делим на такие отрезки наш луч.
Теперь смотрим на координаты точек.
F(4). Делаем 4 шага от ноля (то есть отсчитываем 4 единичных отрезка) и отмечаем точку F(пишем ее название над точкой). Под точкой пишем ее координату.
E(7) Делаем 7 шагов от ноля (то есть отсчитываем 7 единичных отрезков) и отмечаем точку E (пишем ее название над точкой). Под точкой пишем ее координату.
G(12) Делаем 12 шагов от ноля (то есть отсчитываем 12 единичных отрезков) и отмечаем точку G(пишем ее название над точкой). Под точкой пишем ее координату.
Какую еще важную вещь мы можем отметить? Мы всегда делали шаг длиной в одну клетку. То есть наши шаги по координатному лучу всегда были одинаковыми. И это очень важно. Предположим, тебя попросили измерить шагами длину тротуара. Если ты сначала пойдешь мелкими шажками, а потом будешь идти широкими шагами и скажешь, что насчитал 25 шагов, твои измерения не будут верными, ведь шаги были разными.
Важно, чтобы шаги всегда были одинаковыми. Поэтому, если уж мы выбрали шаг длиной в одну клетку, то мы так и будем шагать 1 клетку. Такие одинаковые шаги называются единичными отрезками. Почему единичными? Потому что мы каждый такой отрезок принимаем за какое-то количество единиц.Сейчас мы с тобой решили, что у нас 1 единичный отрезок обозначает одну единицу (но как мы увидим дальше, 1 единичный отрезок может обозначать и большее количество единиц).
Всегда ли мы должны рисовать единичный отрезок размером в одну клетку? Не самый удобный размер, особенно в тетради, не очень удобно писать большие числа рядом, ведь иногда координатой точки может быть не только однозначное, но и двузначное и трехзначное число, тяжело, уместить такой «адрес» под точкой, если у тебя для этого всего одна клетка, попробуй и сам увидишь. Но мы же можем взять отрезок равный двум клеткам, трем клеткам, четырем клеткам и так далее. И скажем себе: «Я беру отрезок равный двум клеткам, пусть он обозначает единицу». Но как ты можем увидеть на рисунке, чем длиннее единичный отрезок, тем меньше чисел мы можем записать на нашем координатном луче. Посмотри, когда единичный отрезок был равен 1 клетке, мы записали числа от 0 до 28. Когда он был равен 2 клеткам, от 0 до 15 так далее. То есть ты всегда должен подумать, сколько чисел ты должен уместить на луче.
Если же нам нужно вместить как можно больше чисел на координатный луч, мы можем брать единичный отрезок меньше 1 клетки, например, половину клетки и даже меньше.
Но ЗАПОМИНАЕМ: все единичные отрезки на одном координатном луче должны быть одной длины.
Как выбрать единичный отрезок?
Предположим, нам дали задание отметить на координатном луче точки со следующими координатами: А(100); В(200); С(500). Как нам это сделать? Посмотри на тетрадный лист. Можешь, конечно, пересчитать, но и так понятно, что клеток меньше ста. Как поступим?
Все не так сложно. Если до этого мы считали, что единичный отрезок равен 1, то почему мы не можем сказать: «А в этот раз мы будем считать, что единичный отрезок равен 100 единицам». И выберем любую длину отрезка, которая нам удобна. Пусть это опять же будет 2 клетки. Итак, один единичный отрезок длиной две клетки, мы считаем равным 100 единицам (мы еще можем сказать, что один наш шаг на координатном луче равен 100 единицам, вот шагнули мы и сразу сто единиц прошли). И тогда мы легко можем отметить точки, которые от нас требуют.
Итак, если тебя попросили отметить точки на луче, то ты должен продумать два вопроса:
И давай определимся, какая точка у нас будет правее на координатном луче?
Предположим, на координатном луче имеются две точки: А(123) и В(1123). Какая из них будет расположена правее? Конечно же, та, до которой мы сделали большее количество шагов по координатному лучу. То есть точка В(1123). То есть правее будет та точка, у которой больше координата.