Как выглядит математика 7 класса
Решение простых линейных уравнений
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в пример получилось верное числовое равенство.
Например, возьмем выражение 2 + 4 = 6. При вычислении левой части получается верное числовое равенство, то есть 6 = 6.
Уравнением можно назвать выражение 2 + x = 6, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое при подстановке на место неизвестной уравнивает выражения справа и слева.
Решить уравнение значит найти все возможные корни или убедиться, что их нет.
Решить уравнение с двумя, тремя и более переменными — это два, три и более значения переменных, которые обращают данное выражение в верное числовое равенство.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Какие бывают виды уравнений
Уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные.
Особенность преобразований алгебраических уравнений в том, что в левой части должен остаться многочлен от неизвестных, а в правой — нуль.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа. Что поможет в решении: Числовой коэффициент — число, которое стоит при неизвестной переменной. Кроме линейных и квадратных есть и другие виды уравнений, с которыми мы познакомимся в следующий раз: Онлайн-курсы по математике за 7 класс помогут закрепить новые знания на практике с талантливым преподавателем. Как решать простые уравненияЧтобы научиться решать простые линейные уравнения, нужно запомнить формулу и два основных правила. 1. Правило переноса. При переносе из одной части в другую, член уравнения меняет свой знак на противоположный. Для примера рассмотрим простейшее уравнение: x+3=5 Начнем с того, что в каждом уравнении есть левая и правая часть. Перенесем 3 из левой части в правую и меняем знак на противоположный. Можно проверить: 2 + 3 = 5. Все верно. Корень равен 2. Решим еще один пример: 6x = 5x + 10. Перенесем 5x из правой части в левую. Знак меняем на противоположный, то есть на минус. Приведем подобные и завершим решение. 2. Правило деления. В любом уравнении можно разделить левую и правую часть на одно и то же число. Это может ускорить процесс решения. Главное — быть внимательным, чтобы не допустить глупых ошибок. Применим правило при решении примера: 4x=8. При неизвестной х стоит числовой коэффициент — 4. Их объединяет действие — умножение. Чтобы решить уравнение, нужно сделать так, чтобы при неизвестной x стояла единица. Разделим каждую часть на 4. Как это выглядит: Теперь сократим дроби, которые у нас получились и завершим решение линейного уравнения: Рассмотрим пример, когда неизвестная переменная стоит со знаком минус: −4x = 12 Если знак минус стоит перед скобками, и по ходу вычислений его убрали — важно не забыть поменять знаки внутри скобок на противоположные. Этот простой факт позволит не допустить обидные ошибки, особенно в старших классах. Напомним, что не у каждого линейного уравнения есть решение — иногда корней просто нет. Изредка среди корней может оказаться ноль — ничего страшного, это не значит, что ход решения оказался неправильным. Ноль — такое же число, как и остальные. Способов решения линейных уравнений немного, нужно запомнить только один алгоритм, который будет эффективен для любой задачки. Чтобы быстрее запомнить ход решения и формулу линейного уравнения, скачайте или распечатайте алгоритм — храните его в телефоне, учебнике или на рабочем столе.
Примеры линейных уравненийТеперь мы знаем, как решать линейные уравнения. Осталось попрактиковаться на задачках, чтобы чувствовать себя увереннее на контрольных. Давайте решать вместе! Пример 1. Как правильно решить уравнение: 6х + 1 = 19. Пример 2. Как решить уравнение: 5(х − 3) + 2 = 3 (х − 4) + 2х − 1. 5х − 15 + 2 = 3х − 12 + 2х − 1 5х − 3х − 2х = −12 − 1 + 15 − 2 Ответ: х — любое число. Пример 3. Решить: 4х = 1/8. Пример 4. Решить: 4(х + 2) = 6 − 7х. Ответ: −2/11 или −(0,18). О десятичных дробях можно почитать в другой нашей статье. Пример 5. Решить: Пример 6. Как решить линейное уравнение: х + 7 = х + 4. 5х — 15 + 2 = 3х — 2 + 2х — 1 Пример 7. Решить: 2(х + 3) = 5 − 7х. Как выглядит математика 7 класса
Выражения и их преобразования☑ 1. Степенью числа а с натуральным показателем n, большим 1, называют произведение n множителей, каждый из которых равен а: ☑ 2. Свойства степеней с натуральными показателями: а m • а n = а m+nПри умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают. (а m ) n = а mnПри возведении степени в степень основание оставляют прежним, а показатели перемножают. (ab) n = а n b nПри возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают. Степенью одночлена называют сумму показателей степеней всех переменных, входящих в одночлен. Например, степень одночлена –8а 2 b 4 равна 6. ☑ 4. Многочленом называют сумму одночленов. Например, 3х 5 – 4х 2 + 1, 7a 3 b – ab 2 + ab + 6 —многочлены. Одночлены считают многочленами, состоящими из одного члена. Степенью многочлена стандартного вида называют наибольшую из степеней входящих в него одночленов. Например, степень многочлена 5х 3 у + 3х 2 у 5 + ху равна степени одночлена 3х 2 у 5 , т. е. равна 7. Степенью произвольного многочлена называют степень тождественно равного ему многочлена стандартного вида. ☑ 5. При сложении многочленов пользуются правилом раскрытия скобок : если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знак каждого слагаемого, заключённого в скобки. Например, (3аb + 5с 2 ) + (ab – с 2 ) = 3ab + 5с 2 + ab – с 2 = 4аb + 4с 2При вычитании многочленов пользуются правилом раскрытия скобок: если перед скобками стоит знак «минус», то скобки можно опустить, изменив знак каждого слагаемого, заключённого в скобки. Например, (6x 2 – у) – (2x 2 – 8у) = 6х 2 – у – 2х 2 + 8у = 4х 2 + 7уЧтобы умножить одночлен на многочлен, нужно умножить этот одночлен на каждый член многочлена и полученные произведения сложить. Например, а 2 (3аb – b 3 + 1) = 3а 3 b – а 2 b 3 + а 2Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить. Например, (5х – 1)(3х + 2) = 15x 2 – Зx + 10x – 2 = 15x 2 + 7x – 2☑ 6. Формулы сокращённого умножения: (а + b) 2 = а 2 + 2аb + b 2Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого и второго выражений, плюс квадрат второго выражения. (а – b) 2 = а 2 – 2аb + b 2Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого и второго выражений, плюс квадрат второго выражения. (а + b) 3 = а 3 + 3а 2 b + 3ab 2 + b 3Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения. (а – b) 3 = а 3 – 3а 2 b + Заb 2 – b 3Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения. (а – b)(а + b) = а 2 – b 2Произведение разности двух выражений и их суммы равно разности квадратов этих выражений. а 3 + b 3 = (а + b)(a 2 – аb + b 2 )Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности. а 3 – b 3 = (а – b)(a 2 + ab + b 2 )Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы. ☑ 7. Разложением многочлена на множители называют представление многочлена в виде произведения многочленов. Для разложения многочленов на множители применяют вынесение общего множителя за скобки, группировку, формулы сокращённого умножения. Например, многочлен 5х 3 – х 2 у можно разложить на множители, вынеся за скобки х 2 : Многочлен 3х – 3у – ах + ау можно разложить на множители, используя способ группировки: 3х – 3у – ах + ау = (3x – 3у) – (ах – ау) = 3(х – у) – а (х – у) = (х – у)(3 – а).Многочлен а 4 – 25x 2 можно разложить на множители, используя формулу разности квадратов двух выражений: а 4 – 25x 2 = (а 2 ) 2 – (5x) 2 = (а 2 – 5x)(а 2 + 5x).Иногда многочлен удаётся разложить на множители, применив последовательно несколько способов. Алгебра 7 класс Все формулы УравненияРешить уравнение с одной переменной — значит найти все его корни или доказать, что корней нет. ☑ 9. Уравнения с одной переменной, имеющие одни и те же корни, называют равносильными. Например, уравнения x 2 = 25 и (х + 5)(х – 5) = 0 равносильны. Каждое из них имеет два корня: –5 и 5. Уравнения, не имеющие корней, также считают равносильными. При решении уравнений с одной переменной используются следующие свойства: Если а = 0 и b ≠ 0, то уравнение ах = b не имеет корней. Например, уравнение 0 • х = 7 не имеет корней. Если а = 0 и b = 0, то корнем уравнения ах = b является любое число. Уравнения с двумя переменными, имеющие одни и те же решения, называют равносильными. Уравнения с двумя переменными, не имеющие решений, также считают равносильными. В уравнении с двумя переменными можно переносить слагаемые из одной части в другую, изменяя их знаки, и обе части уравнения можно умножать или делить на одно и то же число, не равное нулю. При этом получаются уравнения, равносильные исходному. ☑ 12. Линейным уравнением с двумя переменными называют уравнение вида ах + by = с, где х и у — переменные, а, b и с — числа. ☑ 13. Графиком уравнения с двумя переменными называют множество точек координатной плоскости, координаты которых являются решениями этого уравнения. Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов при переменных не равен нулю, является прямая. ☑ 14. Решением системы уравнений с двумя переменными называют пару значений переменных, обращающую каждое уравнение системы в верное равенство. Например, пара чисел х = 7, у = –1 — решение системы Решить систему уравнений — значит найти все её решения или доказать, что решений нет. Системы уравнений с двумя переменными, имеющие одни и те же решения, называют равносильными. Системы, не имеющие решений, также считают равносильными. ☑ 15. Для решения систем линейных уравнений с двумя переменными используются графический способ, способ подстановки, способ сложения. При графическом способе строят графики линейных уравнений (прямые) и анализируют их расположение: При решении системы двух линейных уравнений с двумя переменными способом подстановки поступают следующим образом: При решении системы двух линейных уравнений с двумя переменными способом сложения поступают следующим образом: Алгебра 7 класс Все формулы ФункцииНезависимую переменную иначе называют аргументом, а о зависимой переменной говорят, что она является функцией этого аргумента. Все значения, которые принимает независимая переменная, образуют область определения функции. Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. Графиком линейной функции у = kx + b является прямая. Число k называют угловым коэффициентом прямой, являющейся графиком функции у = kx + b. Графики двух линейных функций пересекаются, если их угловые коэффициенты различны, и параллельны, если их угловые коэффициенты одинаковы. Линейную функцию, задаваемую формулой у = kx при k ≠ 0, называют прямой пропорциональностью. График прямой пропорциональности есть прямая, проходящая через начало координат. При k > 0 график расположен в первой и третьей координатных четвертях, а при k у = х 2 — парабола. Этот график проходит через начало координат и расположен в первой и второй координатных четвертях. Он симметричен относительно оси у. График функции у = х 3 проходит через начало координат и расположен в первой и третьей координатных четвертях. Он симметричен относительно начала координат. Статистические характеристики☑ Средним арифметическим ряда чисел называют частное от деления суммы этих чисел на число слагаемых. Модой ряда чисел называют число, которое встречается в данном ряду чаще других. Ряд чисел может иметь более одной моды или не иметь моды совсем. Медианой упорядоченного ряда чисел с нечётным числом членов называют число, записанное посередине, а медианой упорядоченного ряда чисел с чётным числом членов называют среднее арифметическое двух чисел, записанных посередине. Например, медиана ряда чисел 17, 21, 27, 29, 32, 37, 41 равна 29, а медиана ряда чисел 28, 43, 54, 56, 58, 62 равна 55. Медианой произвольного ряда чисел называют медиану соответствующего упорядоченного ряда. Размахом ряда чисел называют разность между наибольшим и наименьшим из этих чисел. Вы смотрели Конспект «Алгебра 7 класс Все формулы и определения» — краткий курс алгебры за 7 класс. Цитаты взяты из учебника для общеобразовательных учреждений (авт. Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова под ред. С.А. Теляковского). Выберите дальнейшие действия: Учим алгебра 7 класс. Как решать уравнения алгебра 7 класс, примеры, дроби, функции, степени, модулиВ 7 классе ученикам предстоит научиться решать уравнения, дроби, строить функции, разбираться в модулях. Для этого следует познакомиться с основными понятиями в темах, рассмотреть алгоритм решения и пошагово учиться находить ответы. Главное правило — начать с простых примеров, постепенно переходя на более сложные. Большинство задач можно решать несколькими методами (это касается и примеров), следует выбрать самый простой и удобный для себя. Как решать уравнения алгебра 7 классНачнем с решения линейных уравнений (на рисунке показано, по какому принципу они устроены). Чтобы найти ответ в таких уравнениях, нужно совершать действия: раскрытие скобок, поиск подобных слагаемых, умножение/деление частей на одно и тоже число, перенос слагаемых из одной части уравнения в другую. Всё зависит от конкретного примера.
Рассмотрим несколько примеров пошагового решения линейных уравнений. Пример 1.
Можно рассуждать проще: чтобы упростить уравнение, нужно из левой части отправить в правую число 24, поменяв его знак. Равенство сохранится (на рисунке ниже).
Пример 2.
Это уравнение более сложное. Здесь важно запомнить несколько моментов: Пример 3.
В рассмотренных уравнениях корень точно определён. Так получается не всегда. Пример 4.
В этом примере корней нет, так как любое число, которое умножают на 0, будет равно 0 (21 никак не получится). Как решать систему уравнений алгебра 7 классСистемой называют несколько уравнений, в которых нужно найти такие значения неизвестных, чтобы равенство сохранилось. Разберемся на примерах, как выглядят системы и какие методы их решения существуют. метод подстановкиИз самого названия следует, что алгоритм требует что-то подставлять. Ниже представлена система, где нужно найти значения x и y.
Смотрим на систему. Видим, что удобнее будет выразить x во втором уравнении (так как он один). Выражаем путем переноса за знак «равно» 12y. Получилось: x = 11 — 12y (не забываем менять знак при переносе числа). В первое уравнение вместо «x» записываем получившееся выражение. Меняем только x, остальное сохраняется в прежнем виде.
Далее преобразуем уравнение, в которое поместили выражение. Раскрываем скобки (перемножаем 5 на каждое значение). y оставляем в левой части, числа переносим в правую, знаки меняем. Таким образом нашли значение y (y = 1).
Теперь подставляем полученную единицу во второе уравнение (x = 11 — 12y).
метод сложенияЧтобы решить систему методом сложения, нужно из двух уравнений сделать одно. Просто складываем первое и второе. Здесь «y» просто сократились, и получилось простое уравнение. Как только нашли значение «х», нужно подставить его в любой пример (здесь поставили во второе уравнение). В ответе пишется так: (4; 3) — первым всегда пишется х, затем у.
графический метод
Выбирайте самый удобный способ решения. Третий метод — графический, считают самым неточным. Как решать дроби 7 класс Дроби можно разделить на 2 основных вида: Они различаются в способе написания (смотрите рисунок ниже). В свою очередь и те, и другие делятся еще на несколько видов.
Для начала рассмотрим решение примеров с десятичными дробями.
Особое внимание при решении стоит уделить запятым. При сложении и вычитании запятые стоят строго друг под другом, при умножении это не имеет значения.
Примеры 7 класс как решатьТеперь закрепим решение дробей на примерах. Решение примера, представленного ниже: Но можно было решить проще. Первое действие всегда в скобках. Поэтому от 5,25 отнимаем 2,15. Получится 3,1. Умножаем ее на 3 — вышло 9,3. И отнимаем: 10,4 — 9,3 = 1,1. Этот способ даже проще, потому что не нужно следить за знаками при раскрытии скобок.
Чтобы верно решить следующий пример, нужно:
Как решать задачи алгебра 7 классЗадачи решаются путем составления уравнений.
Другие примеры задач с подробными решениями в видео-материалах. Как решать функции алгебра 7 клас сФункцией принято считать зависимость y от x. При этом x является переменной (или аргументом), а у — это значение функции (зависимая переменная). Чтобы найти значение у, которое бы соответствовало определенному значению х, нужно просто это значение х подставить в функцию.
Как решать степени алгебра 7 классЕсли требуется взять какое-либо число несколько раз, то проще записать его в степени. Например, нужно двойку взять три раза, т. е.: 2 * 2 * 2. Получается длинная запись. Поэтому придумали писать так: 2³ (читается: два в третьей степени). |
|---|
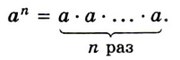Степенью числа а с показателем 1 называют само число а: а 1 = а. 
так как является верным каждое из равенств 7 + (–1) = 6 и 2 • 7 – (–1) = 15.