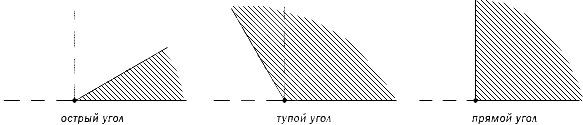
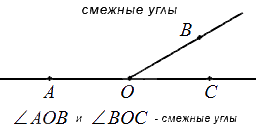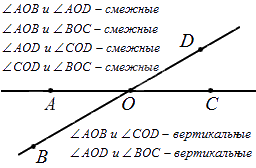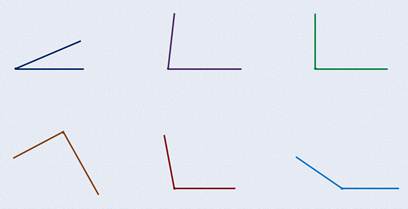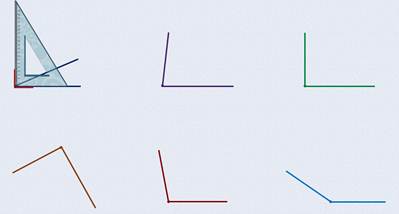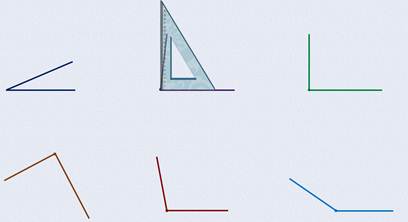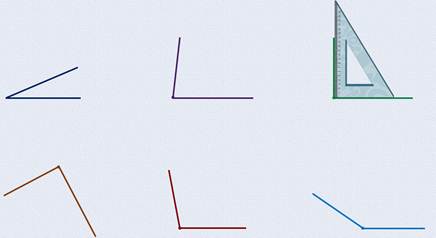Как выглядит острый угол и тупой
Геометрическая фигура угол: определение угла, измерение углов, обозначения и примеры
Угол – основная геометрическая фигура, которую разберем на протяжение всей темы. Определения, способы задания, обозначения и измерения угла. Разберем принципы выделения углов на чертежах. Вся теория проиллюстрирована и имеет большое количество наглядных чертежей.
Определение угла
Угол – простая важная фигура в геометрии. Угол напрямую зависит от определения луча, который в свою очередь состоит из базовых понятий точки, прямой и плоскости. Для досконального изучения необходимо углубиться по темам прямая на плоскости – необходимые сведения и плоскость – необходимые сведения.
Понятие угла начинается с понятий о точке, плоскости и прямой, изображенной на этой плоскости.
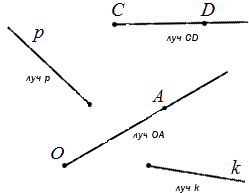
Обозначение луча допустимо в двух вариациях: одной строчной или двумя прописными буквами латинского алфавита. При обозначении двумя буквами луч имеет название, состоящее из двух букв. Рассмотрим подробнее на чертеже.
Перейдем к понятию определения угла.
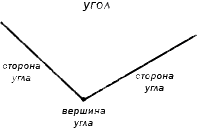
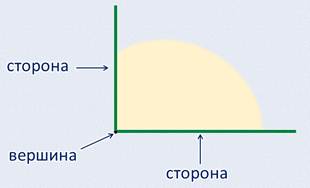
Угол – это фигура, расположенная в заданной плоскости, образованная двумя несовпадающими лучами, имеющими общее начало. Сторона угла является лучом, вершина – общее начало сторон.
Имеет место случай, когда стороны угла могут выступать в роли прямой линии.
Когда обе стороны угла расположены на одной прямой или его стороны служат как дополнительные полупрямые одной прямой, то такой угол называют развернутым.
На рисунке ниже изображен развернутый угол.
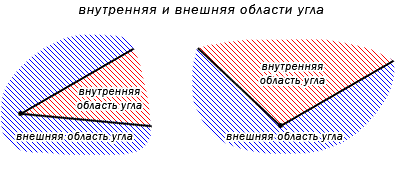
Угол делит плоскость на две части. В случае, если угол не развернутый, тогда одна часть плоскости имеет название внутренняя область угла, другая – внешняя область угла. Ниже приведено изображение, объясняющее, какие части плоскости внешние, а какие внутренние.
При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.
Внутренняя область угла – элемент, служащий для второго определения угла.
Углом называют геометрическую фигуру, состоящая из двух несовпадающих лучей, имеющих общее начало и соответствующую внутреннюю область угла.
Данное определение является более строгим, чем предыдущее, так как имеет больше условий. Оба определения не желательно рассматривать отдельно, потому как угол – это геометрическая фигура, преобразованная при помощи двух лучей, выходящих из одной точки. Когда необходимо выполнять действия с углом, то под определением понимают наличие двух лучей с общим началом и внутренней областью.
Определение смежных и вертикальных углов
Два угла называют смежными, если имеется общая сторона, а две другие являются дополнительными полупрямыми или образуют развернутый угол.
На рисунке видно, что смежные углы дополняют друг друга, так как являются продолжением один другого.
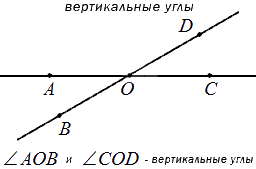
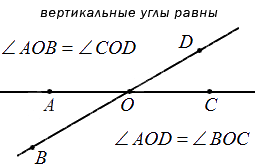
Два угла называют вертикальными, если стороны одного являются дополнительными полупрямыми другого или являются продолжениями сторон другого. На рисунке ниже показано изображение вертикальных углов.
При пересечении прямых получается 4 пары смежных и 2 пары вертикальных углов. Ниже показано на рисунке.
Сравнение углов
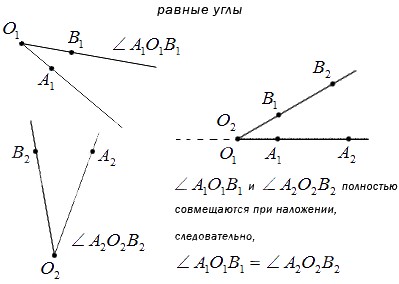
Статья показывает определения равных и неравных углов. Разберем какой угол считается большим, какой меньшим и другие свойства угла. Две фигуры считаются равными, если при наложении они полностью совпадают. Такое же свойство применимо для сравнения углов.
Даны два угла. Необходимо прийти к выводу, равные эти углы или нет.
Известно, что имеет место наложение вершин двух углов и стороны первого угла с любой другой стороной второго. То есть при полном совпадении при наложении углов стороны заданных углов совместятся полностью, углы равные.
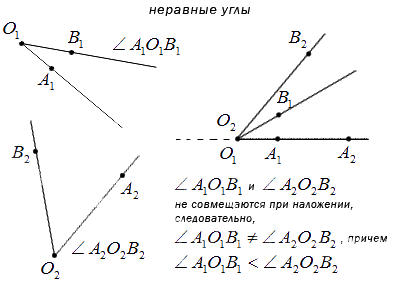
Может быть так, что при наложении стороны могут не совместиться, то углы неравные, меньший из которых состоит из другого, а больший имеет в своем составе полный другой угол. Ниже изображены неравные углы, не совмещенные при наложении.
Развернутые углы являются равными.
Измерение углов
Измерение углов начинается с измерения стороны измеряемого угла и его внутренней области, заполняя которую единичными углами, прикладывают друг к другу. Необходимо посчитать количество уложенных углов, они и предопределяют меру измеряемого угла.
Единица измерения угла может быть выражена любым измеряемым углом. Имеются общепринятые единицы измерения, которые применяют в науке и технике. Они специализируются на других названиях.
Чаще всего используют понятие градус.
Один градус называют углом, который имеет одну сто восьмидесятую часть развернутого угла.
Известно, что количество положенных градусов в угле, это и есть та самая мера угла. Развернутый угол имеет 180 уложенных углов в своем составе. Ниже на рисунке приводятся примеры, где уложение угла идет в 30 раз, то есть одна шестая развернутого, и 90 раз, то есть половина.
Минутой называют одну шестидесятую часть градуса.
Секундой называют одну шестидесятую часть минуты.
Градус содержит 3600 секунд. Минуты обозначают « ‘ », а секунды « » ». Имеет место обозначение:
Градусная мера угла –это число, показывающее количество укладываний градуса в заданном угле.
Исходя из этого, можно сделать вывод, что сумма всех смежных углов равна 180 градусам, потому что они все и составляют развернутый угол.
Кроме градусов, минут и секунд используется еще одна единица измерения. Она называется радианом. Чаще всего ее можно встретить в тригонометрии при обозначении углов многоугольников. Что же называют радианом.
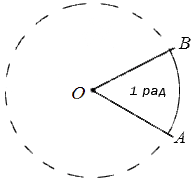
Углом в один радиан называют центральный угол, который имеет длину радиуса окружности равную длине дуги.
Обозначение угла принимается за «рад». То есть запись в 5 радиан сокращенно обозначается как 5 рад. Иногда можно встретить обозначение, имеющее название пи. Радианы не имеют зависимости от длины заданной окружности, так как фигуры имеют некое ограничение при помощи угла и его дугой с центром, находящимся в вершине заданного угла. Они считаются подобными.
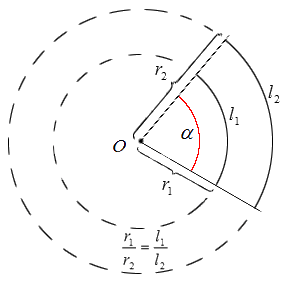
Радианы имеют такой же смысл, как и градусы, только разница в их величине. Чтобы это определить, необходимо вычисленную длину дуги центрального угла поделить на длину ее радиуса.
На практике используют перевод градусов в радианы и радианы в градусы для более удобного решения задач. Указанная статья имеет информацию о связи градусной меры с радианной, где можно подробно изучить переводы из градусной в радианную и обратно.
Обозначение углов на чертеже
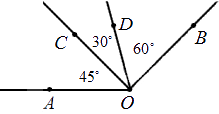
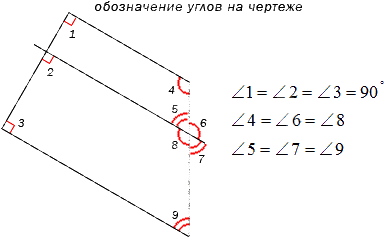
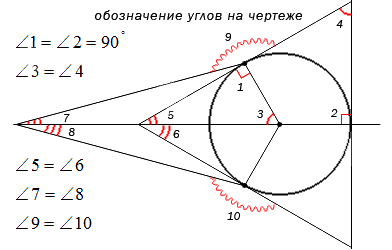
Для наглядного и удобного изображения дуг, углов используют чертежи. Не всегда можно правильно изобразить и отметить тот или иной угол, дугу или название. Равные углы имеют обозначение в виде одинакового количества дуг, а неравные в виде разного. На чертеже изображено правильное обозначение острых, равных и неравных углов.
Когда необходимо отметить более 3 углов, используются специальные обозначения дуг, например, волнистые или зубчатые. Это не имеет столь важное значение. Ниже приведен рисунок, где показано их обозначение.
Обозначение углов должны быть простыми, чтобы не мешали другим значениям. При решении задачи рекомендовано выделять только необходимые для решения углы, чтобы не загромождать весь чертеж. Это не помешает решению и доказательству, а также придаст эстетичный вид рисунку.
Урок 22. Математика 2 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Помните, как выглядит план наших парадных залов? Мы хотели поставить буфет в один из углов золотого зала. Но, сколько не пытались это сделать, у нас толком ничего не получилось. Если мы приставляли его к одной стене, то между буфетом и другой стеной оставалось пространство. Тогда мы попытались поставить буфет в зелёный зал. Там он вообще не входил ни в один из углов.
— Мы так устали. И теперь просто не представляем, что же нам делать, куда можно поставить наш волшебный буфет.
— Плюс, слышишь, наш компьютер включился. Наверное, сейчас нам по скайпу будет звонить царица Математика.
— Ах, мои дорогие Плюс и Минус! Очень обидно, что прежде чем двигать по всему замку буфет, вы не познакомились с темой «Виды углов». Придётся сегодня мне объяснить вам эту тему.
— Что же такое угол? Если мы поставим точку, а от этой точки проведём прямую, у нас получится прямая, ограниченная с одной стороны точкой. Такая линия называется луч. А если из этой же точки мы проведём ещё один луч, то у нас получится угол. При этом точка, из которой были проведены лучи, называется вершиной угла, а сами лучи в этом случае называются стороны угла.
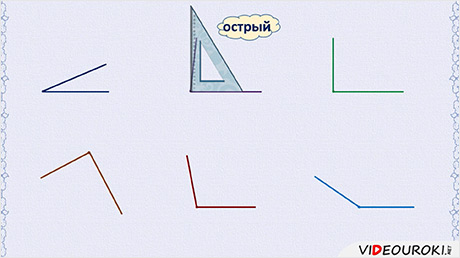
Посмотрите, какие разнообразные углы можно построить:
Среди них вы можете увидеть и острые, и прямые, и тупые углы.
— Начнём мы с прямого угла. Посмотрите на этот лист бумаги. Сейчас мы перегнём его вдвое, потом ещё раз вдвое. Только сгибать надо аккуратно. Так, чтобы линии сгиба совместились и не выглядывали одна из-под другой. Наш лист сложен в 4 раза. И вот получился угол. Такой угол, который образуется аккуратным сгибанием листа в четыре раза, называется прямым углом.
А сейчас развернём лист бумаги:
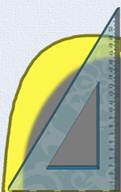
Видите, на нём видны линии сгиба. И у нас видны уже четыре угла с одной общей вершиной. А ещё есть специальная линейка—треугольник. У неё один угол прямой и два острых. Сейчас мы положим такую линейку на наш лист бумаги так, чтобы вершины прямого угла линейки и углов на бумаге совместились. А теперь попытаемся совместить стороны. Получилось?
— Да, стороны прямого угла треугольника точно легли на стороны прямого угла на бумаге.
— Теперь так же положим линейку и на остальные три угла. Как видите, и здесь совмещаются стороны. Значит точно, все эти углы одинаковые. Все они – прямые.
— Я хочу вам показать один угол. Видите, он такой острый, что его вершиной даже можно слегка уколоться.
А теперь посмотрите, угол развернулся, раскрылся. Его вершиной уже вряд ли можно уколоться. Теперь угол стал тупым:
А теперь давайте вернёмся к тем углам, которые мы нарисовали. Сейчас на первый угол кладём линейку.
Вершина линейки совмещается с вершиной угла. Одна из сторон линейки совместилась со стороной угла, а вот вторая спряталась под треугольником. Значит, угол раскрыт меньше, чем прямой угол треугольника. Такие углы, которые раскрыты меньше прямого угла, называются острыми углами.
Посмотрите на следующий угол. Он раскрыт значительно шире первого, но, когда мы прикладываем к нему линейку:
Видно, что одна из сторон опять спряталась под линейку. Значит, этот угол тоже острый.
Переходим к следующему углу:
Его вершина и стороны точно совместились с вершиной и сторонами прямого угла линейки. Как вы думаете, какой это угол?
— Совершенно верно. Этот угол прямой. А вот этот?
— Наверное, острый. Видите, как он наклонился.
— А если приложить линейку? Ну что, какой угол?
— Я ошибся… Этот угол тоже прямой………….
— Ну что же, продолжим. Рассмотрим следующий угол:
Посмотрите, между второй стороной линейки и стороной нарисованного угла как будто ещё один уголок появился. Значит, этот угол раскрыт немного шире, чем прямой. Такие углы, которые раскрыты больше прямого угла, называются тупыми углами.
— Ну, а если посмотреть на последний угол, то здесь даже без линейки-треугольника понятно, что он тупой.
— Да, это очень хорошо видно. Но мы всё-таки приложим линейку и к нему:
Ну что, Плюс и Минус, вы поняли, какие бывают углы?
— А еще прямые углы у учебников и тетрадей.
— У школьных парт и столов.
— И у нашего волшебного буфета тоже все углы прямые.
— Значит, поставить его можно только туда, где стены образуют прямой угол. Посмотрите ещё раз внимательно на план парадных залов.
Ну, где вы можете найти прямой угол?
— Мне кажется, я вижу два прямых угла в синем зале. Но, всё-таки, проверю-ка я это при помощи линейки:
Урра! Получилось! В синем зале- 2 прямых угла. Вот если бы мы сначала поработали с планом парадных залов, не пришлось бы волшебный буфет таскать по всему дворцу.
— Ну, а теперь повторите, пожалуйста, чему вы сегодня научились.
— Угол образуется двумя лучами, которые выходят из одной точки.
— Прямой угол можно получить аккуратным сгибанием листа бумаги вчетверо. Но лучше воспользоваться специальной линейкой-треугольником.
— Углы, которые раскрыты меньше прямого угла, называются острыми углами.
— Углы, которые раскрыты больше прямого угла, называются тупыми углами.
Как выглядит острый угол и тупой
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
 |
Обозначение угла
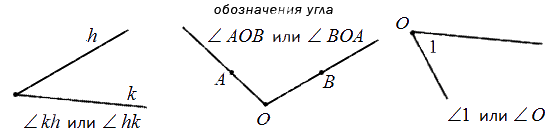
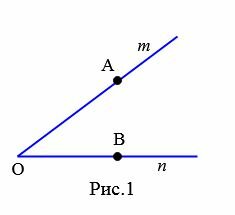
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
Развернутый угол. Внутренняя и внешняя область угла
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
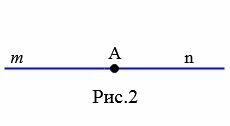 |
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
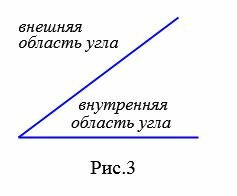 |
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
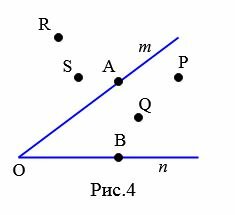 |
Типы углов
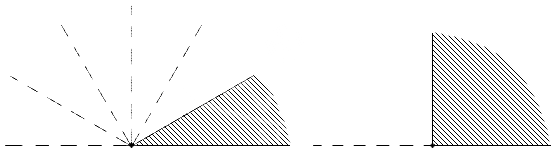
В зависимости от величин, углы бывают следующих типов (Рис.5):
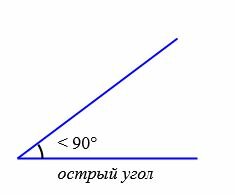 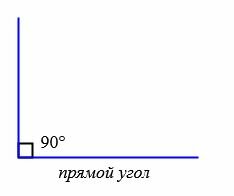 |
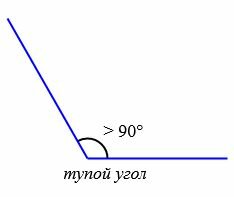  |
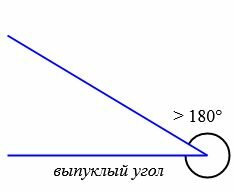 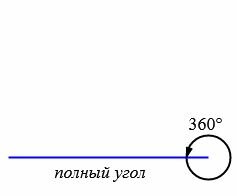 |
Сравнение углов
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
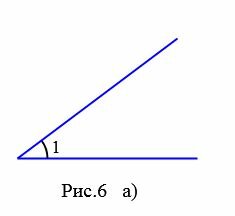 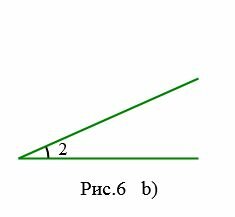 |
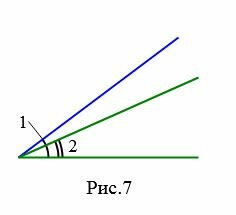
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
 |
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
 |
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Математика
Закажи карту Tinkoff Junior сейчас и получи 200 ₽ на счет
С этой картой можно накопить на мечту, жми ⇒
План урока:
Здравствуйте, дорогие ребята!
Приглашаем вас в сказочную страну Геометрию.
Жил-был король Луч. Была у короля маленькая, смешная и забавная дочка Точка. Отец очень любил и баловал принцессу и никогда не наказывал: не ставил в угол за ее шалости.
Угол. Виды углов: прямой, тупой, острый
Ребята, а вы знаете, что такое угол? Какие бывают углы?
Давайте вместе начертим угол. Сначала поставим точку. Затем проведем из этой точки 2 луча. Например, так:
Лучи – это стороны угла. А точка, из которой мы проводили лучи – вершина угла.
Углы бывают прямые, острые и тупые. Острым углом назовем тот, который меньше прямого, а тупым углом – тот, который больше прямого угла.
Изготовим модель прямого угла из кусочка бумаги.
Можно в качестве модели прямого угла использовать угольник. У него обязательно есть один прямой угол.
Ребята, помогите принцессе Точке определить, какие углы являются прямыми, а какие тупыми и острыми! Сосчитайте, сколько на этом чертеже прямых, острых, тупых углов.
Прямых – 6 углов, острых – 4 угла, тупых – 2 угла.
Король Луч решил построить для принцессы Точки игровую площадку. Он долго размышлял, чертил на песке разные фигуры. Посмотрите, после дождя остались лишь очертания. Назовите одним словом, что это?
Верно, это углы. Запишите номера углов в 3 столбика: острые, тупые, прямые.
Прямоугольник. Свойства противоположных сторон прямоугольника
Ребята, посмотрите на дворец короля и принцессы. Из каких геометрических фигур он состоит?
Давайте сосчитаем все прямоугольники, квадраты, треугольники и круги.
Найдите среди этих фигур четырехугольники, у которых все углы прямые. Воспользуйтесь моделью прямого угла, которую мы с вами изготовили.
Ребята, у принцессы Точки есть для вас вопросы о прямоугольнике. Попробуйте на них ответить.
Вопрос 1. Равны ли у прямоугольника противоположные стороны (они лежат напротив друг друга)?
На чертеже противоположные стороны обозначены одинаковым цветом.
Подумайте! Возьмите любой прямоугольник, измерьте линейкой стороны фигуры, с помощью модели прямого угла или угольника проверьте углы.
Сравните свои выводы с правильными ответами.
Молодцы! Не огорчайтесь, если не все выводы совпали с правильными ответами. Давайте еще раз повторим о прямоугольнике все, что узнали.
Квадрат
Ребята, отвечая на вопрос принцессы Точки, мы сделали вывод о том, что у прямоугольника все стороны могут быть одинаковой длины. Такой прямоугольник будет называться квадратом.
Задача на смекалку от короля. Помогите принцессе Точке ее решить.
Начерти прямоугольник со сторонами 5 см и 4 см. Сделай из него квадрат! Подсказка: «Можно сделать двумя способами: добавить, убрать».
Принцесса отлично справилась с задачей. А теперь попробуйте вы самостоятельно выполнить следующее задание.
Найдите среди этих прямоугольников квадраты. Запишите их номера.
Поиграем вместе с принцессой Точкой. Она выложила из счетных палочек такую фигуру:
Сколько квадратов вы видите? Уберите одну палочку так, чтобы осталось два квадрата. Сделать это можно разными способами. Какие еще фигуры, кроме двух квадратов, у вас получились?
Кроме двух квадратов, на каждом рисунке есть прямоугольник.
Построение прямого угла, прямоугольника, квадрата на клетчатой бумаге
Как вы заметили, король Луч и принцесса Точка любят чертить. Они приглашают нас, ребята, поучаствовать в этом увлекательном занятии. Вооружитесь тетрадью в клеточку, простым карандашом, угольником.
Задание: построить на бумаге в клеточку прямой угол, прямоугольник со сторонами 6 см и 3 см, квадрат со стороной 7 см.
Посмотрите, как получилось у принцессы. Сравните со своими чертежами.
Ставим точку. Откладываем два луча при помощи угольника или линейки.
Ставим точку. Вверх – 3 см, вправо – 6 см. Помним, что противоположные прямоугольника стороны равны. Чертим их – 6 см и 3 см.
А это тетрадь короля. Он чертил квадрат. Сравните со своим чертежом.
Ставим точку. Помним, что у квадрата все стороны равны. Откладываем вверх 7 см, вправо – 7 см. Чертим противоположные стороны по 7 см.
Молодцы, здорово получилось! Если такое занятие было для вас интересным и увлекательным, попробуйте начертить прямой угол, прямоугольник и квадрат на нелинованной бумаге. Сделать это будет гораздо сложнее. Здесь на помощь придет угольник: проверять прямой угол. Можно воспользоваться моделью прямого угла, которую мы изготовили.
Посмотрите, как это получилось у короля и Точки.
После нелегкого занятия король Луч и его дочка присели отдохнуть. Принцесса попросила рассказать интересную сказку. Давайте и мы послушаем!
Сказка
Жил-был на свете Прямоугольник. Фигура важная, спору нет! Люди ценили и уважали Прямоугольника, потому что при изготовлении многих вещей использовали эту фигуру. Всё хорошо у Прямоугольника, но одиноко как-то. Решил он найти своих родственников. Думает: «Если встречу родственников, сразу узнаю, потому что на меня должны быть похожи!».
Однажды встретил Прямоугольник Квадрата и говорит: «Как тебя зовут? Очень ты, брат, на меня похож!». Отвечает Квадрат: «Если найдем не меньше четырех общих признака, значит, родственники». Стали они друг друга рассматривать и обнаружили четыре сходства:
У каждого было по 4 угла, да все прямые, по 4 стороны, да стороны, которые одна напротив другой – одинаковой длины.
Обрадовались родственники, что нашли друг друга. Поспешили вместе отправиться дальше. Встретили однажды Четырехугольника и спрашивают: «Похож ты на нас. Уж не родня ли?».
Говорит им Четырехугольник: «Я был бы очень рад! Если найдем хотя бы два сходства, значит, родственники». Стали опять внимательно друг к другу приглядываться и увидели два общих признака:
Обрадовались фигуры и решили не терять друг друга, держаться всегда рядом.
Понравилась вам сказка? Давайте повторим о фигурах все, что узнали.
В сказочное королевство Геометрия мы вернемся еще не раз. А этот урок подошел к концу. Выберите смайлик вашего настроения.
До скорой встречи в королевстве Геометрия! А сейчас проверьте свои знания. Принцесса Точка справилась с заданиями хорошо, допустила одну небольшую ошибку. Будьте внимательны, не спешите!