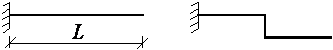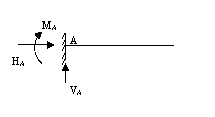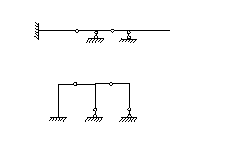Как выглядит статически определимая конструкция
Статически определимые и статически неопределимые системы
Если при рассмотрении заданной системы, находящейся в равновесном состоянии от действия заданных внешних нагрузок, все реакции в связях закрепления, а также внутренние усилия в ее элементах, можно определить только по методу сечений, без использования дополнительных условий, то такая система называется статически определимой.
В реальной практике встречаются такие конструкции при расчете которых одних лишь уравнений равновесия оказывается недостаточно, в связи с чем требуется формулирование дополнительных уравнений, связанных с условиями деформирования конструкции.
Системы, в которых количество наложенных связей больше, нежели число независимых уравнений равновесия, называются статически неопределимыми.
По сравнению со статически определимыми системами, в статически неопределимых системах имеются дополнительные связи, которые называются лишними.
Термин “лишние связи” является условным. Эти связи являются лишними с точки зрения расчетных предпосылок. В действительности эти связи создают дополнительные резервы для конструкций, как в плане обеспечения её жесткости, так и прочности.
На рис. 2.5, а изображен кронштейн, состоящий из двух стержней, шарнирно скрепленных между собой. В связи с тем, что на конструкцию действует лишь вертикальное усилие Р, а система является плоской (т.е. все элементы конструкции и вектор внешних сил лежат в одной плоскости), получается, что усилия в стержнях легко определяются из условий равновесия узла А, т.е.
Раскрывая эти уравнения, получаем замкнутую систему линейных уравнений относительно неизвестных усилий N1 и N2 в которой количество уравнений равно количеству неизвестных:
Если конструкцию кронштейна усложнить, добавив еще один стержень (рис. 2.5, б), то усилия в стержнях N1, N2 и N3 прежним способом определить уже не удастся, т.к. при тех же двух уравнениях равновесия (2.16) имеются уже три неизвестных усилия в стержнях. В таких случаях говорят, что система один раз статически неопределима. Разность между числом неизвестных усилий и количеством независимых (значащих) уравнений равновесия, связывающих эти усилия, называется степенью статической неопределимости рассматриваемой системы.
В общем случае под n-раз статически неопределимой системой понимается система, в которой число неизвестных внешних опорных реакций и внутренних усилий превышает число независимых и значащих уравнений равновесия на n единиц.
Дата добавления: 2015-12-29 ; просмотров: 1328 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Статически определимая система
Статическая система называется статически определимой, если число опорных реакций соответствует числу степеней свободы, и величины опорных реакций по принципу механического равновесия можно определить из величин внешних нагрузок.
Все другие системы называются статически неопределимыми.
Для расчёта всех статически определимых систем достаточно решать уравнения равновесия:
Для плоских задач есть три условия равновесия. Сумма всех вертикальных сил, всех горизонтальных сил и всех моментов должна быть равна нулю. Σ V=0, Σ H=0, Σ M=0.
Для пространственных задач есть шесть условий. Σ X=0, Σ Y=0, Σ Z=0, Σ Mx=0, Σ My=0, Σ Mz=0.
Осадка опор, температурные воздействия и неточности сборки в статически определимых системах не влияют на распределение и величину усилий.
Пример
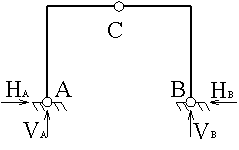
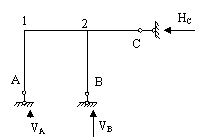
Сумма всех вертикальных сил равна 0. Σ V = 0:
Сумма всех горизонтальных сил равна 0. Σ H = 0:
Поскольку неизвестных четыре (VA, VB, VC и HA) а уравнения только три, невозможно определить величину всех опорных реакций. Система следовательно статически неопределимая.
Если убрать опору B, то реакцияVB исчезнет и система становится статически определимой.



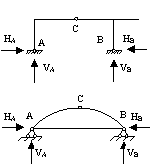
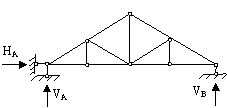
Примеры простых статически определимых систем
Примеры простых статически неопределимых систем
Полезное
Смотреть что такое «Статически определимая система» в других словарях:
СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ СИСТЕМА — (в строительной механике) геометрически неизменяемая система, в которой для определения всех реакций связей (усилий в опорных закреплениях, стержнях и т. п.) достаточно уравнений статики … Большой Энциклопедический словарь
статически определимая система — (в строительной механике), геометрически неизменяемая система, в которой для определения всех реакций связей (усилий в опорных закреплениях, стержнях и т. п.) достаточно уравнений статики. * * * СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ СИСТЕМА СТАТИЧЕСКИ… … Энциклопедический словарь
Статически определимая система — в строительной механике, система конструкций, в которой реакции всех связей (усилия в опорных закреплениях, стержнях и т.п.) при любой нагрузке могут быть определены с помощью уравнений статики (см. Строительная механика). С. о. с.… … Большая советская энциклопедия
СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ СИСТЕМА — в строительной механике геометрически неизменяемая система, в к рой для определения усилий во всех элементах, в т. ч. в опорных связях, достаточно ур ний статики … Большой энциклопедический политехнический словарь
СИСТЕМА СТАТИЧЕСКИ ОПРЕДЕЛИМАЯ — конструктивная система, количество наложенных связей в которой равно числу уравнений статического равновесия (Болгарский язык; Български) статически определима система (Чешский язык; Čeština) staticky určitá soustava (Немецкий язык; Deutsch)… … Строительный словарь
Система, статически определимая — геометрически неизменяемая система, в которой реакции всех связей при любой статической нагрузке могут быть найдены из условий статики. Источник: Справочник дорожных терминов … Строительный словарь
статически определимая механическая система — Механическая система, у которой реакции всех наложенных связей могут быть определены из условий равновесия, получаемых в статике … Политехнический терминологический толковый словарь
СИСТЕМА ОСНОВНАЯ — статически определимая система, полученная для расчёта методом сил из статически неопределимой системы путём освобождения её от дополнительных или лишних связей (Болгарский язык; Български) основна система (Чешский язык; Čeština) základní… … Строительный словарь
основная система — Положенная в основу расчета система, образуемая из заданной статически неопределимой путем отбрасывания или добавления связей или отбрасывания одних и добавления других связей. [Сборник рекомендуемых терминов. Выпуск 82. Строительная механика.… … Справочник технического переводчика
Ферма (технич.) — Ферма (франц. ferme, от лат. firmus √ крепкий, прочный), несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Ф. применяют главным образом в строительстве (покрытия… … Большая советская энциклопедия
изучаем сопротивление материалов
Статически определимые и неопределимые конструкции
Под статически определимой системой понимается такая система, для которой усилия во всех ее элементах могут быть определены с применением лишь уравнений равновесия (т.е. число неизвестных равно числу независимых уравнений равновесия). Если этого сделать нельзя, то такая система называется статически неопределимой системой. В статически неопределимой системе число неизвестных больше числа полезных уравнений равновесия.
Разность между числом неизвестных усилий (реакций опор и внутренних силовых факторов) и числом независимых уравнений равновесия, которые могут быть составлены для рассматриваемой системы, называется степенью статической неопределимости системы. Связи, наложенные на систему, бывают внешними и внутренними. Под внешними понимают ограничения, накладываемые на абсолютные перемещения точек системы, как единое целое. Внутренние же связи ограничивают взаимные (относительные) перемещения элементов системы. Статическая неопределимость системы может быть вызвана как внешними, так и внутренними связями.
Определение реакций в статически неопределимой системе называется раскрытия статической неопределимости. Методы расчета статически неопределимых систем основаны на определении перемещений в точках наложения связей. Любая наложенная связь (любое ограничение движения) позволяет составить дополнительное уравнение, называемое уравнением совместности перемещений. В результате появляется возможность сделать число уравнений равным числу неизвестных и решить полученную систему уравнений.
О независимых и бесполезных уравнениях равновесия
Для всякой пространственной системы сил можно составить систему из
6-и уравнений равновесия и, решив ее, найти 6 неизвестных сил. Однако среди этих уравнений могут быть тождества, обращающиеся в нуль при любых значениях нагрузок. Это бесполезные уравнения и, следовательно, число неизвестных сил должно быть равно числу уравнений минус число тождеств.
Для произвольной плоской системы сил можно составить 3 уравнения, не являющихся тождествами, например, сумму проекций всех сил на 2 любые оси и одну сумму моментов всех сил, относительно какой-либо точки.
Для плоской системы сходящихся сил можно составить лишь 2 независимых уравнения. Сумма моментов всех сил относительно точки их пересечения тождественно равна нулю. Из 2-х уравнений можно определить лишь 2 неизвестные силы.
Для плоской системы параллельных сил бесполезной оказывается сумма проекций на ось, перпендикулярную силам. Поэтому из 2-х уравнений равновесия можно найти лишь 2 неизвестные силы.
Для системы, где силы действуют вдоль одной прямой линии (коллинеарные силы) можно составить лишь одно независимое уравнение — сумму проекций всех сил на эту прямую, которая равна просто сумме сил.
Определение степени статической неопределимости
Рассмотрим плоскую задачу. Необходимое для равновесия число наложенных внешних связей должно быть равно количеству уравнений равновесия − ∑x = 0, ∑y = 0, ∑m = 0 (т.е трем ). Если плоская система состоит из D частей, каждую из которых можно рассматривать как жесткое тело, то количество параметров, определяющих положение этой системы будет равно 3·D. Каждый шарнир, соединяющий две части системы, позволяет лишь их взаимный поворот, устраняя возможность их взаимных смещений − следовательно он уменьшает количество возможных перемещений системы на две единицы. Кроме этого, каждый опорный стержень устраняет возможность перемещения системы в соответствующем направлении. Таким образом, подсчитать степень статической неопределимости системы W, определяемую внешними связями, можно по следующей формуле:
где
D − число частей (“дисков”) системы, каждая из которых может рассматриваться как абсолютно жесткое тело,
Ш − количество шарниров в системе, соединяющих эти “диски”,
С − число опорных стержней (шарнирно-подвижная связь).
Если W=0 – то система статически определимая. При W
iSopromat.ru
Статически определимыми системами (СОС) называют стержневые, балочные конструкции и рамы, во всех элементах которых, для определения внешних и внутренних усилий (в том числе реакций связей) достаточно только уравнений равновесия.
Если же уравнений статики окажется недостаточно, то говорят, что мы имеем дело со статически неопределимыми системами (СНС).
Обычно под расчетом систем понимают оценку их несущей способности, прочности и жесткости.
Типы статически определимых систем
Расчетные схемы статически определимых систем имеют следующий вид:
Рисунок 2.4 – Прямая и ломаная консоль
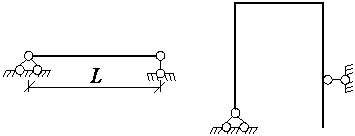
Рисунок 2.5 — Простая балка и рама
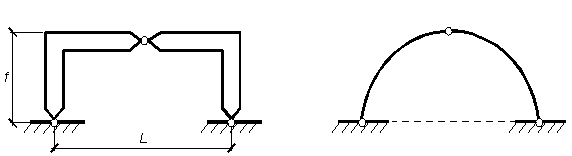
Рисунок 2.6 – Трехшарнирные рама и арка
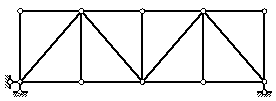
Рисунок 2.20 – Классическая ферма
Рисунок 2.29 – Многопролетная балка
Аналитические способы расчета статически определимых систем
I этап. Определение опорных реакций
Опорные реакции для статически определимых систем определяются при помощи уравнений равновесия:
Для трехшарнирных систем для определения опорных реакций необходимо составить 4 уравнения равновесия:
— для систем без затяжки
При отсутствии горизонтальной нагрузки НА = HB=H.
— для систем с затяжкой
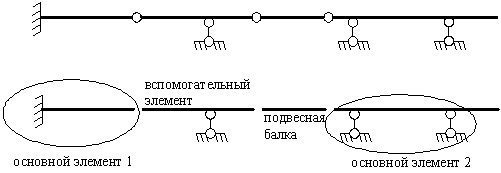
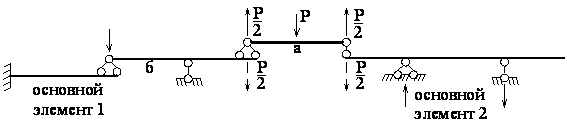
Для многопролетных систем необходимо выделить основные, вспомогательные и подвесные элементы посредством построения поэтажной схемы (согласно рисунка 2.29).
Рисунок 2.30 – Поэтажная схема для схемы рисунка 2.29
После построения поэтажной схемы расчет начинают вести с верхнего этажа.
Нижележащие этажи рассчитываются на приложенную внешнюю нагрузку и передаточное давление.
Передаточное давление равно опорным реакциям верхнего этажа взятого с обратным знаком.
Опорные реакции в фермах находятся также как и в балках.
Варианты статически определимых систем
Рассмотрим основные варианты статически определимых систем, их расчетные схемы и соответствующие уравнения для определения опорных реакций:
Для определения опорных реакций и внутренних усилий требуется построение поэтажной схемы.
II этап. Определение внутренних усилий
Отметим, что в курсе «Строительная механика» практически та же методика расчета, но используется она для более сложных систем.
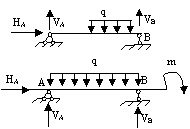
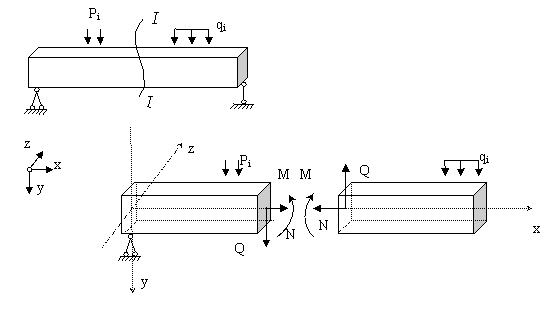
Если мы мысленно отсечем часть некоторой произвольной балки, загруженной произвольной нагрузкой, то в сечении балки в общем случае возникнет комплекс внутренних усилий (рисунок 2.31):
Рисунок 2.31 – Виды внутренних усилий, возникающих в сечении балки
Сформулируем определения внутренних усилий и правила знаков для них.
Изгибающий момент М в сечении I-I представляет собой сумму моментов всех внешних сил, приложенных к рассматриваемой части балки относительно оси OZ.
Момент считается положительным, если он вызывает растяжение нижних волокон рассматриваемой отсеченной части.
Поперечная сила Q — внутреннее усилие, равное по величине сумме проекций всех внешних сил, приложенных к рассматриваемой части балки на ось OY.
Продольная сила N — внутреннее усилие, равное по величине сумме проекций всех внешних сил, приложенных к рассматриваемой части балки на ось ОХ.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Статически определимые и статически
неопределимые системы
В сопромате система называется статически определимой, если число неизвестных в ней равно числу полезных уравнений равновесия.
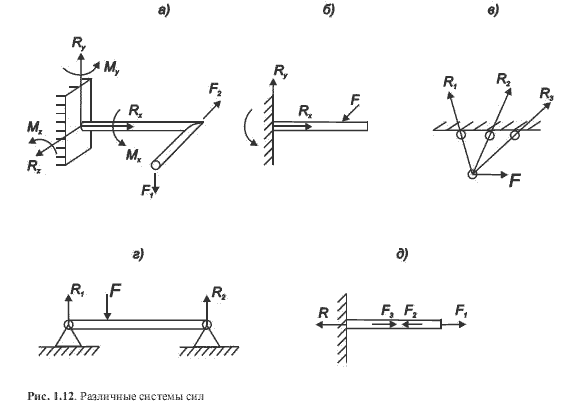
Для всякой пространственной системы сил (рис. 1.12, а) можно составить систему из 6-и уравнений равновесия и, решив ее, найти 6 неизвестных сил. Однако среди этих уравнений могут быть тождества, обращающиеся в нуль при любых значениях нагрузок. Это бесполезные уравнения и, следовательно, число неизвестных сил должно быть равно числу уравнений минус число тождеств.
Для произвольной плоской системы сил (рис. 1.12, б) можно составить 3 уравнения, не являющихся тождествами, например, сумму проекций всех сил на 2 любые оси и одну сумму моментов всех сил, относительно какой-либо точки.
Для плоской системы сходящихся сил (рис.1.12, в) можно составить лишь 2 уравнения, не являющихся тождествами. Сумма моментов всех сил относительно точки их пересечения тождественно равна нулю. Из 2-х уравнений (любых) можно определить лишь 2 неизвестные силы.
Для плоской системы параллельных сил (рис.1.12, г) бесполезной оказывается сумма проекций на ось, перпендикулярную силам. Соответственно из 2-х любых уравнений равновесия можно найти лишь 2 неизвестные силы.
Для системы коллинеарных сил (действующих вдоль одной прямой линии) (рис. 1.12, д) можно составить лишь одно полезное уравнение — сумму проекций всех сил на эту прямую, которая равна просто сумме сил.
Система называется статически неопределимой, если число неизвестных в ней больше числа полезных уравнений равновесия.
Степень статической неопределимости равна разности между числом неизвестных и числом полезных уравнений равновесия.
Для раскрытия статической неопределимости существуют разные способы, которые будут рассмотрены далее. Заметим лишь, что всякая реакция возникает в местах наложения внешних связей (ограничений движения системы). Нет ограничения — нет реакции. Есть ограничение — есть реакция. В то же время любая наложенная связь (любое ограничение движения) позволяет составить дополнительное уравнение, называемое уравнением совместности перемещений В результате появляется возможность сделать число уравнений равным числу неизвестных и решить систему уравнений.
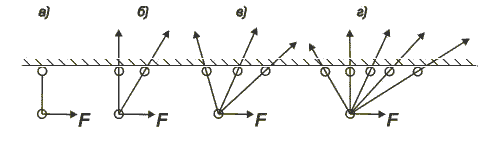
На рис. 1.13 приведены примеры различных систем.
Рис. 1.13. Статически определимые и статически неопределимые системы
Схема а) — стержень недостаточно закреплен, он может свободно вращаться под действием силы. Это механизм. Такие задачи требуют учета сил инерции и рассматриваются в курсе теории машин и механизмов.
Схема б) — система из 2-х стержней статически-определимая, два усилия в 2-х стержнях определяются из 2-х уравнений равновесия.
Схема в) — система из трех стержней 1 раз статически-неопределима: неизвестных усилий — 3, полезных уравнений равновесия—2, степень статической неопределимости 3-2=1.
Схема г) — система 3 раза статически-неопределима: неизвестных усилий — 5, полезных уравнений равновесия—2, степень статической неопределимости 5-2=3.
При большом количестве опор и шарниров определить степень статической неопределимости довольно трудно. Проще это сделать следующим образом:
Мысленно отбрасываем связи по одной до тех пор, пока система не превратится в механизм. Верните на место одну связь (любую). Система станет статически определимой. В таком виде число отброшенных связей равно степени статической неопределимости системы.