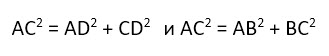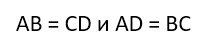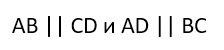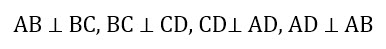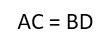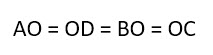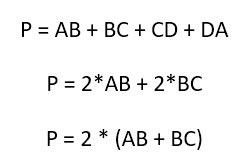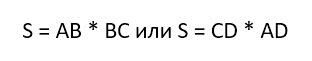Как выглядят прямоугольники 2 класс
Что такое прямоугольник: определение, свойства, признаки, формулы
В данной публикации мы рассмотрим определение, свойства и признаки одной из основных геометрических фигур – прямоугольника. Также приведем формулы, с помощью которых можно найти его площадь и периметр.
Определение прямоугольника
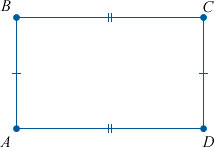
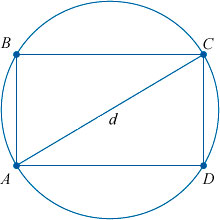
Прямоугольник – это четырехугольник, у которого все углы равны 90° (т.е. являются прямыми).
∠ABC = ∠BCD = ∠BAD = ADC = 90°
Прямоугольник состоит из:
Сам прямоугольник обычно записывается путем перечисления его вершин, например, ABCD в нашем случае.
Примечание: Прямоугольник является разновидностью параллелограмма.
Свойства прямоугольника
Свойство 1
Противоположные стороны прямоугольника попарно параллельны и равны.
Свойство 2
Длина и ширина прямоугольника одновременно являются его высотами, т.к. они взаимно перпендикулярны.
Свойство 3
Если соединить середины сторон прямоугольника, то получится ромб.
Свойство 4
Квадрат диагонали (d) прямоугольника равняется сумме квадратов его смежных сторон.
d 2 = a 2 + b 2
Это следует из теоремы Пифагора, которую можно применить к любому из прямоугольных треугольников, которые образуются в результате деления диагональю прямоугольника.
Свойство 5
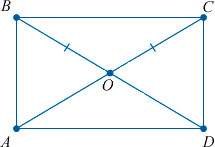
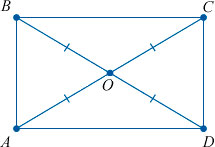
Диагонали прямоугольника равны, и в точке пересечения делятся пополам.
Свойство 6
Около любого прямоугольника можно описать окружность, радиус (R) которой равен половине диагонали этого прямоугольника.
Следовательно, диаметр окружности равен полной длине диагонали прямоугольника.
Признаки прямоугольника
Параллелограмм является прямоугольником, если верно одно из следующих утверждений:
Формулы
1. Площадь прямоугольника (S):
2. Периметр прямоугольника (P):
Прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это.
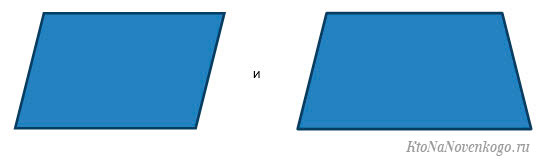
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
Диагонали прямоугольника
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
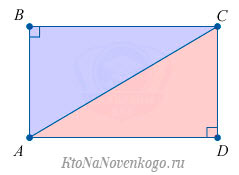
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (5)
Главная основа геометрии — это все же треугольник. Через него можно построить любую фигуру и доказать любую теорему.
Не согласен с утверждением, что раз один угол прямой, то перед нами точно прямоугольник, всё же прямоугольник — это когда все противоположные стороны параллельны друг другу, а если только один угол прямой, то там и трапеция может быть.
Я бы сказала, что прямоугольник — это основа архитектуры. Все здания так или иначе используют эту фигуру в своем дизайне.
Вот за что я люблю прямоугольники, так за то, что площадь его легко найти, да и периметр, вот с трапецией сложнее, увы, но те же земельные участки больше трапеции, отсюда и земельные споры.
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 36. Прямоугольник
Перечень вопросов, рассматриваемых в теме:
— знакомство с прямоугольником.
Прямоугольник – четырёхугольник, у которого все углы прямые.
Геометрия – раздел математики, изучающий пространственные отношения и формы.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.2. – 8-е изд. – М.: Просвещение, 2017. – с.14-15.
2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.2. – 7-е изд., дораб. – М.: Просвещение, 2017. – с.23.
Теоретический материал для самостоятельного изучения
Рассмотрите фигуры. У всех четыре угла. Можно заметить, что одна из фигур имеет только прямые углы. Это прямоугольник
Рассмотрим фигуру с одним прямым углом. Это треугольник.
Рассмотрим фигуру с прямыми углами. Это четырехугольник.
Четырехугольник относится к группе прямоугольников.
Определить, что углы прямые можно с помощью треугольника, прикладывая его в каждый угол: угол D, затем угол С, затем угол В, и угол А.
Значит, фигуры, у которых все углы прямые, можно назвать прямоугольники.
У прямоугольника четыре стороны. Вертикально расположена ширина, обычно меньшая сторона.
Но прямоугольниками можно назвать только те четырёхугольники, у которых все углы прямые.
Горизонтально расположена длина, обычно большая сторона.
Обратите внимание на написание слова: длина.
Запомните, как это слово пишется!
1. Найдите на картинке прямоугольники и определите их количество.
Прямоугольников на этой картинке 10.
2. Найдите прямоугольники и запишите их номера:

Презентация по математике на тему «Прямоугольник» (2 класс)
Описание презентации по отдельным слайдам:
40 – 6 = 34 Т 52 – 3 = 49 И 33 – 8 = 25 Е 17 + 9 = 26 О 48 – 7 = 41 Р 65 – 5 = 60 Я М 30 – 3 = 27 20 – 7 = 13 Г 26 + 4 = Е 30 13 25 26 27 30 34 41 49 60 Г Е О М Е Т Р И Я
Геометрия- это раздел математики, изучающий пространственные отношения и формы
Купили 6 кг риса и 7 кг гречки, а манки – столько, сколько гречки и риса вместе. Сколько манки купили? (13 кг) В куске ткани было 42 м. Утром продали 12 м, а вечером – 10 м. Сколько метров осталось? (20 м) В школу фигуристов принимают детей не старше 7 лет. Примут ли меня в эту школе на будущий год, если сейчас мне ровно 5.
Держи ручку правильно Минутка чистописания
Что такое прямоугольник?
Вывод: Четыре угла. Все углы прямые. Противоположные стороны равны. Четыре стороны. У прямоугольника –
. № 2 Работа по учебнику
. Работа по учебнику № 2
. Работа по учебнику № 2
Работа по учебнику № 2
Работа по учебнику № 2
Чемодан – в него вы положите знания, которые получили сегодня на уроке и повезете с собою потому, что они пригодятся вам в дальнейшем. Ксерокс – это знания, которые вы получили сегодня на уроке, и вы поделитесь ими с другими людьми (мамой, папой, бабушкой, друзьями, соседями и др.) Мясорубка – это знания, которые вы получили сегодня на уроке, переработаете, и может быть когда-нибудь используете. Корзина – это знания, которые вы получили сегодня на уроке вам не пригодятся, и вы выбросите их в мусор. РЕФЛЕКСИЯ
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-996528
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Петербургский Политех перевел студентов на дистанционку
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Минпросвещения создает цифровую психологическую службу для школьников
Время чтения: 1 минута
Минздрав включил вакцинацию подростков от ковида в календарь прививок
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Урок математики во 2-м классе по теме «Прямоугольник. Квадрат»
1) Выявить существенные свойства прямоугольника и квадрата, сформировать способность к их распознаванию на основе существенных свойств, умение изображать их, вычислять периметр прямоугольника и квадрата.
2) Развивать вычислительные навыки, закреплять правила порядка действий в выражениях со скобками, развивать речь, логическое мышление, умение применять полученные знания в реальной жизни.
3) Воспитывать внимательность, активность, чувство товарищества.
Оборудование: мультимедийная установка, карточки с примерами, числами, прямоугольники и квадраты на каждого ученика, листы формата А2, маркеры, индивидуальные доски.
I. Организационный момент.
— Ребята сейчас урок математики. На уроке мы будем как всегда думать, сотрудничать, для этого нам надо быть внимательными, организованными, сообразительными, уметь слушать друг друга.
II. Актуализация знаний.
— Сегодня ребята мы попадём в интересную страну Геометрия, населённую удивительными жителями. А как зовут этих жителей, нам помогут узнать эти выражения.
— Установите принцип соединения примеров, продолжите, найдите значения выражений.
(Ответы примеров развешаны по всему классу. Дети решают пример, находят ответ и вывешивают его на доску)
77, 63, 90, 20, 41, 7, 21
— Какое число лишнее? Почему? (7-однозначное, а остальные двузначные)
— Расставьте числа в порядке убывания. (90, 77, 63, 41, 21, 20). Теперь давайте посмотрим, какие буквы спрятались за этими числами. (Фигуры)
— Геометрические фигуры и населяют страну Геометрия, они очень дружны с другими её жителями. (Слайд 1. Презентация)
— Рассмотрите чертёж. Что на нём изображено? (Углы)
— При помощи, каких прямых линий образует прямой угол? (Перпендикулярные прямые)
— Какой инструмент помогает нам определить прямой угол? (Треугольник.)
— А где мы можем встретит углы?
III. Постановка темы и задач (2 слайд).
— Посмотрите на чертёж. Что изображено на чертеже? (Фигуры)
— Но не все эти фигуры помогут нам на уроке. Какая фигура лишняя и почему? (Круг – он без углов, треугольник – у него 3 угла, ромб – нет прямых углов)
— Какие геометрические фигуры остались? (Прямоугольник и квадрат)
— Кто догадался, какая тема урока? Кто может назвать, сформулировать её?
Тема урока: “Прямоугольник. Квадрат”.
Задачи. Вспомнить и уточнить знания о прямоугольнике и квадрате. Дать определение этим фигурам, узнать какие признаки они имеют. А так же учиться применять свои знания и умения в различных видах работ.
IV. Открытие новых знаний.
1. Прямоугольник. (Работа с раздаточным материалом – прямоугольник)
— Что же такое прямоугольник? Внимательно рассмотрите свой прямоугольник. Что вы о нём можете сказать?
— Сколько у прямоугольника углов? (4)
— Как можем назвать фигуру?
— Значит это четырёхугольник.
— Какие углы у прямоугольника? (Углы все прямые)
— Как это доказать? (Проверить с помощью прямоугольника)
— Измерьте теперь стороны прямоугольника. Что можете сказать? (Противоположные стороны равны)
— Кто знает, как называется большая сторона прямоугольника? (Длина)
— Давайте обобщим наши исследования прямоугольника. (Слайд 3)
а) Работа с карточкой (проверка слайд 4).
Задание.
1) Обведите замкнутой линией все прямоугольники на чертеже.
2) Обведите замкнутой линией все квадраты на чертеже.
— Возьмите карточку, прочитайте задание и выполните его. Проверьте, так ли у вас получилось.
— Что вы заметили? (Что квадраты находятся внутри множества прямоугольников). Почему? (Это тоже прямоугольник)
— Докажите (работа с раздаточным материалом квадрат).
— Четыре угла значит четырёхугольник, все углы прямые. Из этого следует, что квадрат прямоугольник. Но это особенный прямоугольник. Что же в нём особенного? (У квадрата все стороны равны)
— Докажите. Измерьте стороны квадрата.
Так что же такое квадрат? (Ответы детей проверяем на слайде 5)
Здравствуй, лес – необычный лес,
Полный сказок и чудес!
(Широко разводят руки в стороны. Повороты вправо и влево с вытянутыми руками)
Ты о чём шумишь листвою
Ночью тёмной, грозовою?
(Руки подняты вверх. Выполняются покачивающиеся движения вправо – влево)
Кто в глуши твоей таится?
Что за зверь? Какая птица?
(Всматриваются вдаль, держа округлённую ладонь над бровями, поворачиваясь при этом в правую и левую сторону)
Всё открой, не таи.
Ты же видишь – все свои.
(Широко разводят руки в стороны. Прижимают обе ладони к груди)
Упражнения для глаз
VI. Закрепление пройденного.
1. Работа с правилами в учебнике стр. 50-51.
2. Различие прямоугольников и квадратов. №3, стр. 51 (Проверка слайд 6)
Прямоугольников – 3 DАЕF, FEBC, DABC
— Почему квадрат включили в группу прямоугольников? (Квадрат является прямоугольником так, как у него 4 угла и все они прямые)
3. Построение прямоугольника и нахождение его периметра. № 5(а) или № 5(б), стр. 51 (по выбору).
Два ученика выполняют задание на индивидуальных досках. Коллективная проверка.
— Что нужно найти? (Периметр)
— Что такое периметр? (Периметр – это сумма длин всех сторон)
— Какой закон сложения применяли? (Сочетательный)
4. Работа в группах. №7, стр.51. (Выполняется на больших листах маркерами)
Составить выражения и вычислить их значение удобным способом (проверка у доски).
5. №10, стр.53 (если будет время).
А – 3, В – 5, С – 1, Д – 2, Е – 4
VII. Рефлексия. Итог.
— Поднимите руку те, кому понравилось наше путешествие?
— Что открыли нового для себя?
— Какие знания не являются для вас открытием, так как вы уже это знали ранее?
— Найдите прямоугольники вокруг нас.
— Как вы думаете, а зачем мы всё это учили. Где эти знания могут пригодиться?
— Королева Страны Геометрия была бы очень довольна вашей работой на уроке и поэтому прислала вам пропуск в свою страну. А как он выглядит, вы мне скажите сейчас сами. Если к четырёхугольнику прибавить ещё один угол, какая фигура получится? (Пятиугольник. Слайд 7)
VIII. Домашнее задание.
— Но и д/з она даёт каждому своё. Найти периметр своей комнаты (слайд 8).
Просьба Королевы — сделать на уроке труда снежинки с узором из геометрических фигур.