Как выкроить пройму для начинающих
15 шагов — базовая выкройка платья с рукавом пошаговая инструкция
Базовая выкройка платья с рукавом — это основной этап в конструировании. Но и самый сложный, особенно для новичка. Сегодня я вам покажу пошагово, как я строю выкройку, и как всегда постараюсь его сделать понятным и наглядным. Желаю вам, чтобы к концу этого мастер класса у каждого из вас была собственная базовая выкройка платья с рукавом!
Если вы еще не знаете сколько плюсов и возможностей открывает для портного такая выкройка, я вам сейчас расскажу.
Индивидуальное лекало повышает качество посадки изделия по фигуре, сокращает или вовсе сводит к нулю количество внесения изменений во время примерки, а так же минимизирует число примерок до одного. Сначала мои клиенты удивлялись, что я приглашаю их на примерку всего единожды, так как привыкли бегать в ателье по три — четыре раза, но мой метод — это про быстро и просто. Я по натуре человек — лентяйка, и если можно что — то упростить или автоматизировать, то обязательно это сделаю.
Почему нужна базовая выкройка
Ну что, вам тоже хочется облегчить себе шитье? Тогда давайте учится строить выкройку сами.
Какую методику конструирования я буду использовать
В конструировании я использую метод ЕМКО. Он расшифровывается как Единый метод конструирования одежды, его придумали еще в советскую эпоху, он проверен временем и до сих пор его с успехом используют в работе ведущие ателье и Дома мод.
На самом деле, в конструировании существует множество технологий — это английская система, Мюллер и сын, ЦОТШЛ и прочие. И в конечном итоге при построении по одной из них, получается лекало для той модели, которое запланировано. Но с высоты своего многолетнего опыта могу сказать, что лучшая методика — это опыт! Только пробуя и экспериментируя, постоянно работая и изучая новое можно найти ту самую систему для построения идеальных выкроек.
Метод конструирования — это инструмент в руках портного. Поэтому можно не останавливаться на одной системе, брать для себя лучшее из каждой и черпать новое.
Поэтому советую вам не грешить на методику, если ваше изделие не село на фигуру идеально, проанализируйте свою работу, возможно вы допустили ошибки в расчетах.
Для построения базовой выкройки платья мне понадобились
Прибавки на свободу облегания для базовой выкройки платья
Прежде чем приступить к построению основы нужно знать, что мерки в выкройке закладываются не «чистыми», а с прибавками. Что это за значения? Прибавки — это величина определяющая свободу облегания изделия. Здесь мы будем брать прибавки, предназначенные для максимального облегания по фигуре, то есть для платья.
Прибавки в расчетах обозначаются с приставкой — П. У меня в построении будут фигурировать такие виды прибавок, как:
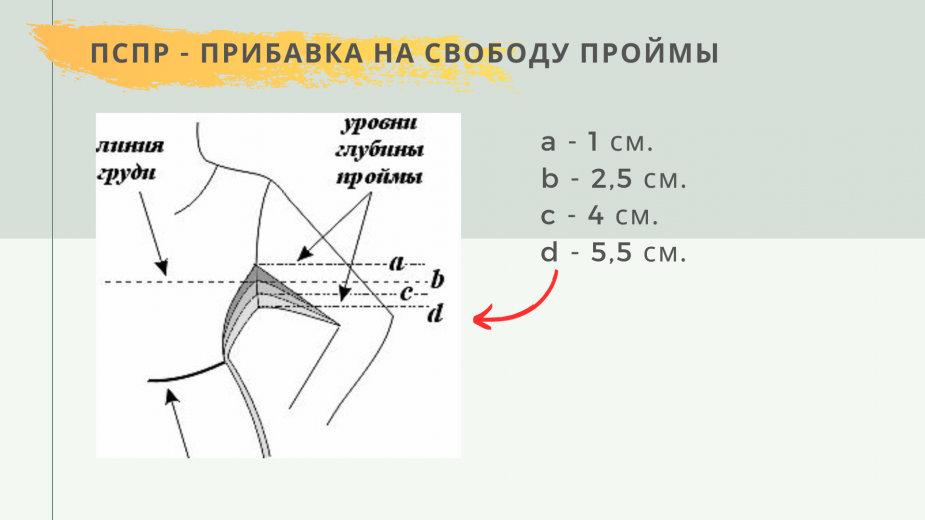
На рисунке можно наглядно увидеть как прибавка Пспр определяет уровень прилегания рукава по пройме. В зависимости от значения прибавки, которое вы выберете при построении, будет зависеть какой рукав получите в готовом изделии.
Базовая выкройка платья с рукавом пошаговая инструкция
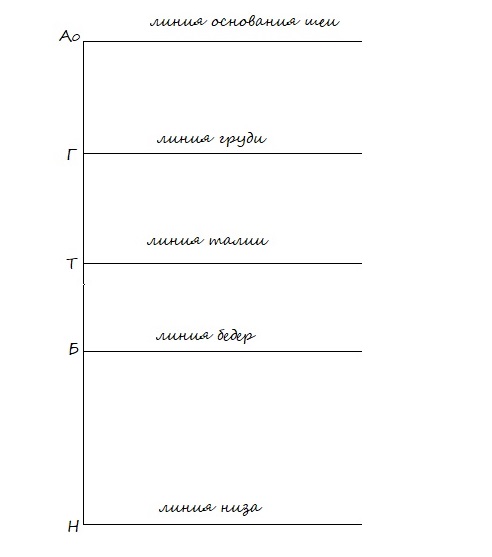
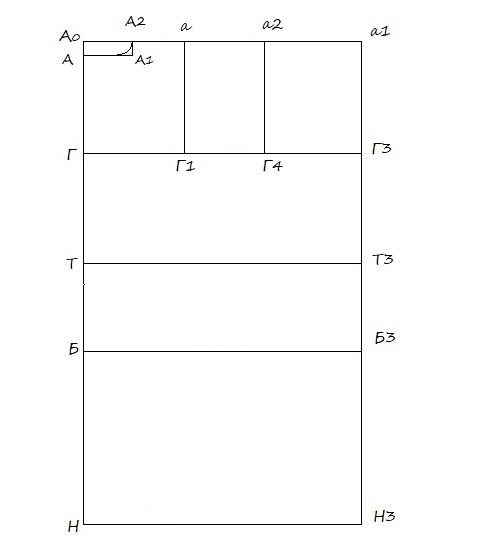
Создание конструкции основы платья начинается с построения прямоугольника или сетки и нанесения основных линий. В построении я буду использовать сокращения, принятые для мерок:
Расчет сетки
01. Строю прямой угол с вершиной в точке Н.
Н Т — от точки Н вверх мерка Дю
Линия основания шеи:
Т А0 — от точки Т вверх мерка Дтс
02. Линия проймы (груди):
Т Г — от точки Т вверх мерка Вбоч – Пспр (2,5 см.)
Т Б — от точки Т вниз 0,4 * Сб
04. Ширина сетки у меня зависит от мерки Обхват груди (Ог), поэтому:
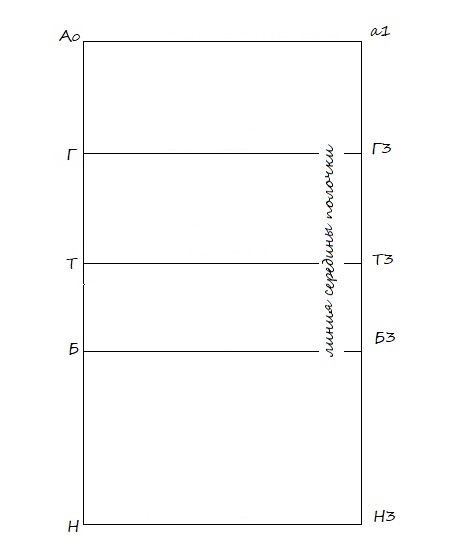
Г Г3 = от точки Г откладываю мерку Сг3 + Пг (3 см.)
Через Г3 провожу линию середины полочки. Обозначаю на чертеже получившиеся при этом точки — а1, Г3, Т3, Б3, Н3.
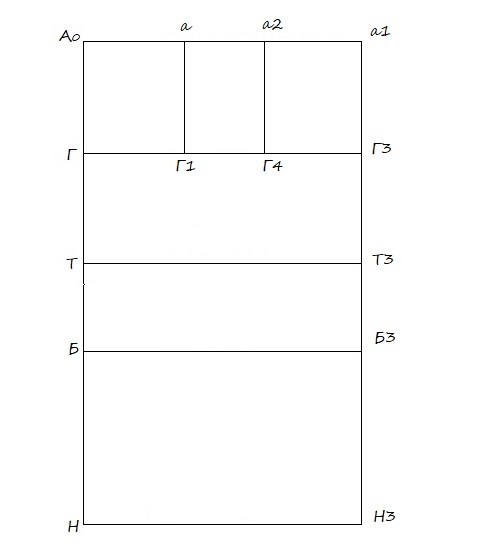
Г Г1 = откладываю мерку Шс + Пшс (1 см.), из точки Г1 провожу вверх вертикаль Г1а
Как проверить правильность расчета величины «Ширина проймы»? Для каждого размера есть свои величины, поэтому я всегда сверяюсь с таблицей:
| Вид изделия | Минимальная ширина проймы для изделий с втачным рукавом на типовые фигуры (см.) для размеров | ||||||||
| 44 | 46 | 48 | 50 | 52 | 54 | 56 | 58 | 60 | |
| Платье | 11 | 11,6 | 12,2 | 12,8 | 13,4 | 14 | 14,6 | 15,2 | 15,8 |
Оставшееся значение (Г4 Г3) — это ширина полочки. При этом ширина спины и ширина полочки не должны сильно отличаться.
Расчет спинки
07. Ширина горловины:
А0 А2 = мерка Сш/3 + Пшг (1 см.)
Строю прямоугольник и оформляю с помощью лекала округлую горловину.
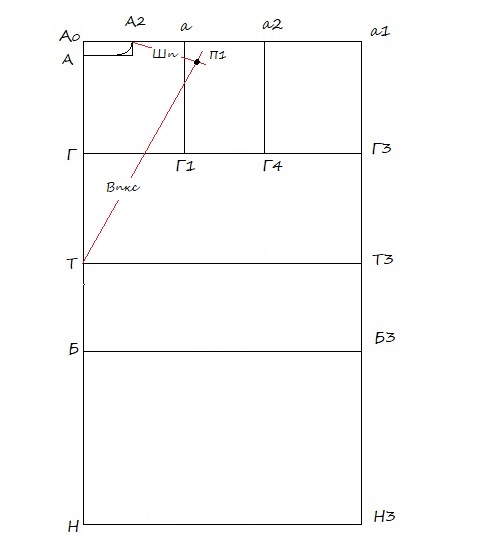
08. Построение конечной плечевой точки — П1:
Из точки А2 откладываю отрезок равный Шп, при этом из точки Т откладываю отрезок равный Впкс. На пересечении этих двух измерений: мерки Шп и мерки Впкс — получаю точку П1.
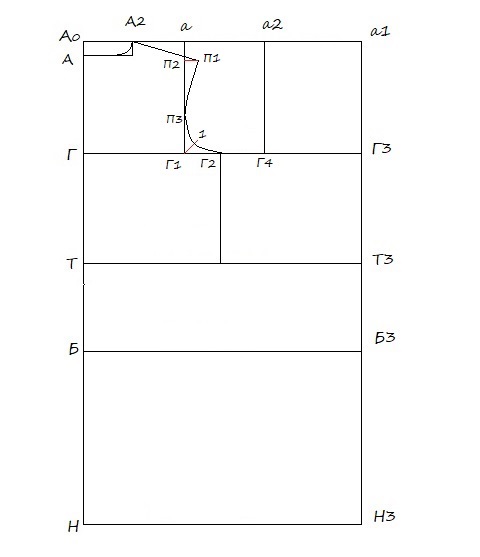
09. Построение проймы:
П1 П2 = опускаю перпендикуляр из П1 к линии Г1 а
Контрольная точка спинки (П3):
Г1 П3 = (Г1 П2 / 3) + 2
Биссектриса (Г1 1) = 0,2 * Г1 Г4 + 0,5
Соединяю точки П1, П3, 1, Г2 плавной кривой, можно с помощью лекала для проймы, при этом в точке П1 угол прямой — 90 градусов
Из точки Г2 вниз опускаю вертикаль на горизонтальную линию талии.
Расчет полочки
10. Т3 А3 — мерка Дтп вверх.
Через точку А3 провожу горизонталь:
Ширина горловины = А0 А2 (с чертежа спинки) – 0,5 см.
А3 А5 — Глубина горловины = А3 А4 + 1 см. Строю прямоугольник и оформляю с помощью лекала округлую горловину.
11. Г3 Г6 — мерка Цг, через точку Г6 провожу вертикаль до линии талии, на пересечении линий получаю точку Т6.
12. Из точки А4 меркой Вг делаю засечку дугой на линии Г6 Т6. Получаю точку Г7 — центр груди. Она может получится как выше линии груди, так и ниже, а может пересечься с ней, это зависит от типа фигуры.
13. Раствор нагрудной вытачки (точка А9):
А4 А9 = 2 (Шг2 – Шг1) +2
На пересечении этих двух измерений: отрезка (А4 А9) и отрезка (Г7 А4) — получаю точку А9.
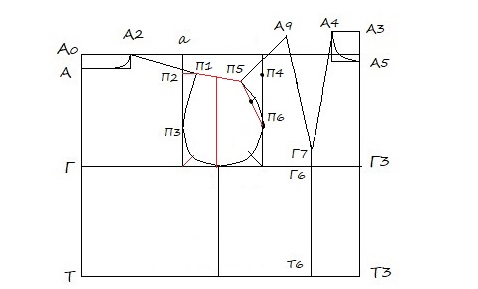
14. Плечевой срез (А9 П5):
Точку П5 получаю пересечением мерки Вппк из точки Г7 на пересечении мерки Шп из точки А9.
Соединяю точку П5 с точкой А9 получаю плечевой срез полочки.
Г4 П4 = Г4 П5 по дуге из точки Г4
Контрольная точка полочки (П6)
Биссектриса (Г4 2) = Биссектриса с чертежа спинки (Г1 1) – 0,5 см.
П6 П5 соединяю прямой и делю полученный отрезок на 2 – получаю точку 3. Из точки 3 откладываю вверх перпендикуляр 0,5 – 1 см. Соединяю точки П5, П6, 2, Г2 плавной кривой – рисую пройму полочки. Помню, что угол в точке П5 – 90
Вытачки
Расчет вытачек = (отрезок Т Т3 – (Ст + Пт) )/ 4.
Полученную разницу распределяю между деталями спинки и полочки в талиевые и боковые вытачки.
Центр талиевой вытачки на спинке проходит посередине отрезка Г Г2, спуск от линии груди Г Г3 на 4 см. вниз, спуск от линии талии Т Т1 на 10 см. вниз
Цент вытачки по полочке проходит по центру груди Г6 Т6, спуск от линии груди Г Г3 на 4 см. вниз, спуск от линии талии Т Т1 на 12 см. вниз.
Для того чтобы построить боковые вытачки по линии бедер нужно посчитать разницу по формуле: отрезок ББ3 — (Сб + Пб). Полученное значение (оно может получится как положительным так и отрицательным, это зависит от типа фигуры) делим пополам.
И отступаем при положительном значении по линии бедер спинки в право, а по полочке влево. При отрицательном значении наоборот. На рисунке ниже боковые срезы перекрещиваются, значит я получила положительную разницу.
При нулевом значении — боковые вытачки встречаются в одной точке.
При отрицательном значении — боковые вытачки находятся в отдалении друг от друга.
Построение чертежа прямого втачного рукава
Построение рукава также начинается с черчения сетки.
01. Высота оката рукава (О1 О2):
На чертеже полочки и спинки соединяю конечные плечевые точки П1 и П5, делю полученный отрезок пополам, опускаю перпендикуляр вниз к линии груди Г Г3. Измеряю длину полученного отрезка — перпендикуляра.
Высота оката рукава (О1 О2) = полученный отрезок минус Пспр (прибавка на свободу проймы) минус «Величина на развитие дельтовидной мышцы руки»:
02. Ширина рукава (О1 Р1) = О1 Р2 = Мерка Ор + Пор (прибавка на обхват рукава)/2
О1 Рп = отрезок О1 Р1 /2
О1 Рл = отрезок О1 Р2 /2
03. Длина рукава (О2 М1) = Мерка Др. Провожу влево и вправо горизонтали, получаю точки М2 и М3.
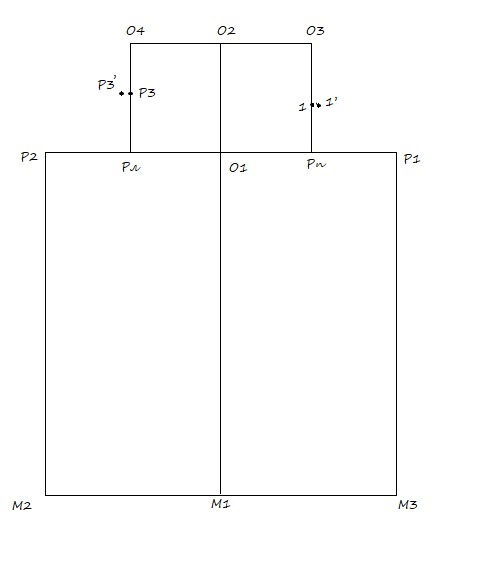
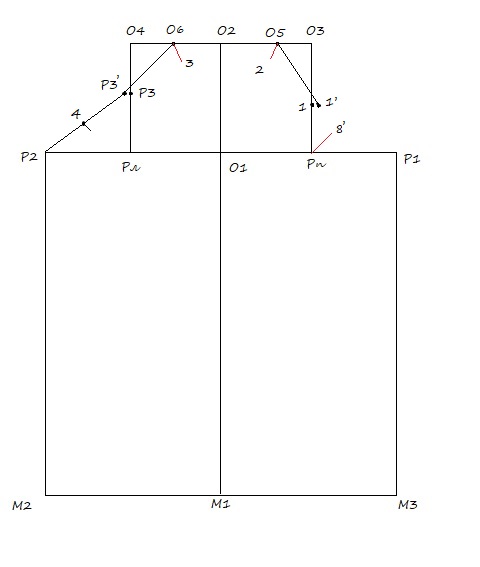
03. Рп 1 = Г4 П6 (контрольная точка с чертежа полочки). От точки 1 отхожу на 0,5 см. вправо ставлю точку 1’
04. Рл Р3 = Г1 П3 (контрольная точка с чертежа спинки). От точки Р3 отхожу на 0,5 см. влево ставлю точку Р3’
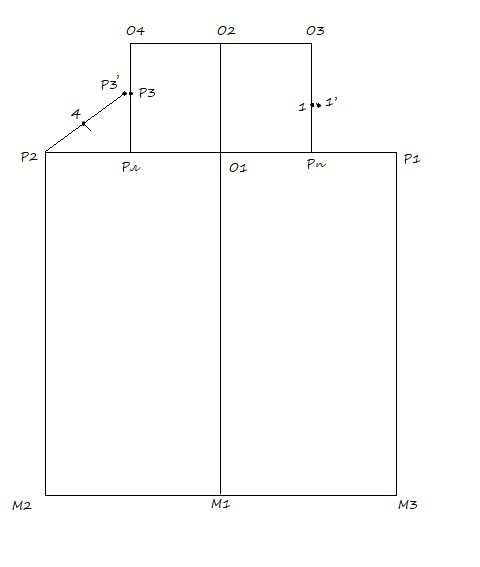
05. Р3’ и Р2 соединяю прямой и делю пополам. Получаю точку 4. От точки 4 перпендикуляр (1-2 см.)
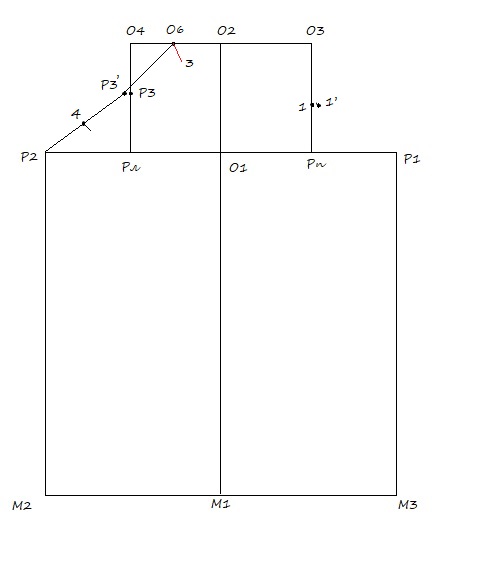
06. О2 О6 = О2 О4 / 2
О6 и О3 соединяю прямой, О6 (3) – биссектриса угла Р3’ О6 О2 = 1 – 2 см.
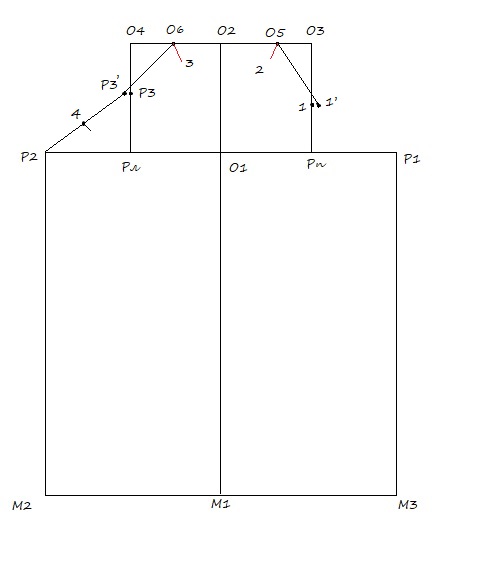
07. О2 О5 = О2 О3 / 2 + 2 см., откладываю полученное значение от О2 до О5.
О5 и 1’ соединяю прямой, О5 (2) – биссектриса угла О2 О5 1’ = 1,5 – 2,5 см.
08. Рп 8’ = биссектриса с чертежа проймы полочки (Г4 2) + 1 см.
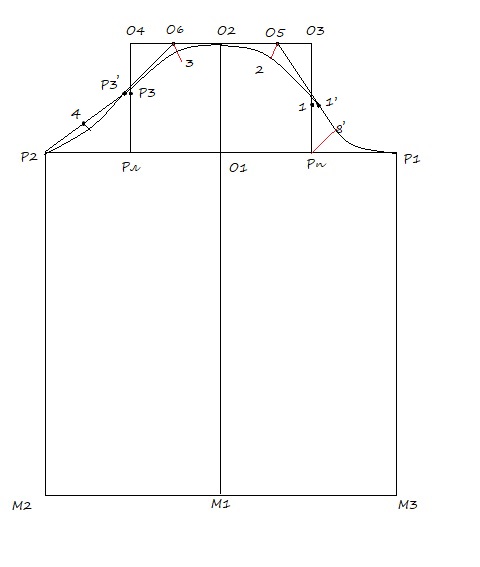
09. Линию оката оформляю плавно соединив точки: Р2, Р3’, 3, О2, 2, 1’, 8’, Р1.
Чертеж расположенный слева от точки О2 — это спинка рукава, справа — его полочка. Контрольная точка центр рукава О2 переносится на 1 см. на полочку.
После построения рукава необходимо проверить длину оката. Она должна соответствовать длине проймы с чертежа основы + (1 — 1,5 см.) на припосаживание.
На этом построение базовая выкройка платья с рукавом пошаговая инструкция закончено. Надеюсь, вы сумели разобраться со всеми расчетами, и у вас получилась собственная выкройка по которой теперь можно шить более ста моделей вещей, и они будут сидеть на фигуре безупречно!
Мои курсы кройки и шитья онлайн для начинающих
Мои основные принципы — это честность, открытость и забота о своих учениках. Я уверена на 100 % в качестве своего продукта. На сегодняшний день в моей школе шитья «Beloshveika_school» есть три направления обучения кройке и шитью для начинающих в формате онлайн:
1) Конструирование — этот курс подойдет тем, кто хочет научится строить выкройки и снимать мерки с фигуры. Для успешного прохождения здесь не нужно быть асом в черчении или иметь какие — то специальные навыки, информации преподносится легко и просто
2) Базовый курс кройки и шитья — это основа основ. Я предлагаю пройти его всем новичкам, кто находится в поиске знаний по шитью и не знает с чего начать. Этот курс был по крупицам собран из моего оффлайн (живых) курсов шитья, которые я преподаю в городе Уфа вот уже с 2014 года. Я знаю на каком этапе у учениц могут возникать трудности, поэтому смогу вам помочь
3) Курс шитья пижам и белья Этот курс родился в процессе работы над мастер классами по домашней одежде, когда я увидела что интерес к ней заслуживает отдельного обучения. На этом курсе мы шьем по готовым выкройкам, поэтому он отлично подойдет совсем начинающим, кто пока боится вникать в процессы построения лекал. Честно говоря, этот курс можно проходить даже вместе с детьми, потому что он интересный, а результат можно получить очень быстро!
Как построить базовую выкройку основы платья несколькими способами (по Мюллеру, в программе «Валентина», по системе 10 мерок)
Если вы решили освоить искусство самостоятельного пошива одежды, то рекомендуем начать с платья. Конечно, фартуки и наволочки – это нужные вещи, но, согласитесь, немного скучные. А сшив платье, вы сразу можете удивить подруг и коллег своим мастерством, похвастаться обновкой. Для пошива, в первую очередь, нужно научиться строить основу. А потом уже можно приступать и к моделированию платья на основе базовой выкройки. Существует несколько методик построения выкроек: авторские, классические, с использованием компьютерных программ и вручную на листе бумаги. Попробуем разобраться в особенностях некоторых из них.
Метод построения базовой выкройки женского платья по Мюллеру
Система кроя, созданная более 125 лет назад немецким портным Михаэлем Мюллером, учитывает индивидуальные особенности фигуры человека, позволяет выполнить точные построения выкроек одежды. Методика не самая простая, но очень точная. По методу Мюллера тело делится на сегменты, особенности фигуры учитываются в пропорциональном расчёте отклонениями от стандарта.
Рассмотрим в качестве примера как выполнить основную выкройку прямого платья.
При построении будем учитывать прибавки (= П) на свободное облегание для размеров:
Для построения основы женского платья нам нужно снять мерки (мы приводим свои данные, вы можете выполнить построение по собственным меркам):
Выполним предварительные расчёты для моделей с ОГ больше 80 см:
Величины, обозначенные **, при выполнении чертежа берём с прибавками на свободное облегание (П).
Для правильно построенного чертежа сумма ((ВПр 3 + П) + (ШС + П) + (ШПр + П) + (ШГ + П)) должна равняться (ОГ : 2 + П) = (ОГ : 2 + 5,0(7,5) см).
Далее разберёмся, как построить выкройки.
Нам потребуется лист кальки с шириной не менее чем (ОГ : 2 + 0,3) м и длиной не менее чем (ДИ + 15 см).
От правого верхнего угла отступаем вниз 10 см, затем влево 5 см, отмечаем точку (∙) О. Проводим прямую вниз. По ней откладываем ОГ = ВПр З + П = 21 см; ОТ = ДТС = 44 см; ОБ = ВБ = 63 см; ОН = ДИ = 1000 см.
Через данные (∙) проводим горизонтальные прямые: через (∙) О – линию верха, через (∙) Г – линию груди, через (∙) Т – линию талии, через (∙) Б – линию бёдер, через (∙) Н – линию низа.
От (∙) Б в левую сторону откладываем 2 см, ставим (∙) Б1. Из (∙) О через (∙) Б1 чертим прямую до пересечения с нижней линией. Обозначаем (∙) пересечения этой прямой с горизонтальными линиями, как показано на чертеже. Мы построили среднюю линию спинки.
Влево от (∙) Г1 откладываем Г1Г2 = ШС + П = 18 см. Далее последовательно отмеряем Г2Г3 = 2/3 (ШПр + П) = 8 см; Г3Г4 = 10 см + 13 см; Г4Г5 = 1/3 (ШПр + П) = 4 см; Г5Г6 = ШГ + П = 19 см.
Контролируем Г6Г4 + Г3Г1 = (ОГ : 2 + П) = 49 см.
Через отмеченные (∙) проводим вертикали – см. чертёж. Линия, проходящая через (∙) Г6 будет средней линией переда.
На пересечении вертикали через (∙) Г2 и горизонтали через (∙) О отмечаем (∙) О1.
От (∙) О в левую сторону откладываем ОО2 = Шш 3 = 6,3 см. В случае большого ОГ величину ОО2 = Шш 3- 0,5 см. Из (∙) О2 поднимаемся вверх на 2 см, это будет (∙) О3. Рисует лекальную линию выката.
Из (∙) О1 отмеряем вниз О1О4 = 1,0(1,5) см. Из (∙) О3 через М О4 проводим прямую. По ней влево отмеряем О4О5 = 1,5(2,0) см (для маленьких размеров), 1,0(1,5) см (для средних размеров), 0(1) см (для больших размеров).
В середине отрезка Г2О4 ставим (∙) П1. Через неё проводим горизонтальную прямую, откладываем влево П1П1’ = 1 см. В центре отрезка П1Г2 ставим (∙) П2. Через неё прочерчиваем горизонталь. На её пересечении с вертикалью из (∙) Г5 отмечаем (∙) П4. В левую сторону от (∙) П2 откладываем П2П3 = 1,3(1,5) см (прямо пропорционально размеру). Из (∙) О5 через П1’П3 до (∙) Г3 рисуем лекальную линию проймы так, чтобы её начало было перпендикулярно плечевой линии.
Проставляем (∙) Т1 и (∙) Т2 на линии талии. По линии груди вправо от (∙) Г6 отмеряем Г6Г7 = ОГ : 10 + 0,5 см = 9 см. Проводим вертикаль, на её пересечении с линией талии ставим (∙) Т4. От неё вверх отмеряем Т4О7 = ДТП 2 = 49,7 см. От (∙) О7 спускаемся на О7Г8 = ВГ 2 = 27,7 см.
Из (∙) Г5 поднимаемся по прямой на Г5О6 = Г2О4 – (1,0…1,5 см). При увеличении наклона плеча увеличиваем вычитаемую величину.
Из (∙)Г8 и (∙) Г5 через М О7 и М О6 делаем радиусные засечки. Величины радиусов Г8О7 и Г5О6.
Из (∙) О6 по дуговой линии отмеряем О6О8 = Ог : 20 – (0,5…1,0) = 3,25 см. Из (∙) О8 чертим дугу радиусом (О3О5 – 1 см) = 14 см. Уменьшение плечевой линии на 1см сделаем для припосаживания. На пересечении дуг ставим (∙) О9.
Далее будем строить пройму переда.
Проводим прямую от (∙) О8 до (∙) П4. В центре отрезка ставим (∙) П5. Из неё влево по перпендикуляру откладываем 1 см, отмечаем (∙) П6. Из (∙) О8 до (∙) Г4 через (∙) П6 и (∙) П4 проводим лекальную линию. При этом вначале она должна быть перпендикулярна плечевой линии.
Из (∙) О7 проводим перпендикуляр на среднюю линию полочки, ставим (∙) О10. Из неё вправо отмеряем 6,3 см (= О10О11 = ШШ з). Для больших значений ГО ширина выката О10О11 = ШШ З – 0,5 см. Глубина выката равна 7,5 см (= О10О12 = ШШ З + 1…2 см). Чертим отрезок О10Г5. По нему откладываем О10О13 = ШШ З + 0,5…0,8 см. Соединяем (∙) О12, (∙) О13, (∙) О11 лекальной линией.
Из (∙) О9 строим отрезок О9О14 = О11О7 = 3 см. Соединив (∙) О14 и (∙) Г8, получаем правую границу вытачки. Из (∙) Г8 вверх отмеряем Г8О15 = Г8О14. Чертим отрезок О11О15.
Чтобы построить вытачку на спинке из (∙) О3 по плечевой линии влево откладываем О3О16 = 3…5 см. Опускаем перпендикуляр на линию лопаток, ставим (∙) Л. Если вы строите основу платья для фигуры с выпуклыми лопатками и выраженной сутулостью, то по проведённой линии нужно сделать разрез. Лекало раздвигается, формируется вытачка. В нашем случае мы этого делать не будем, так как нет необходимости.

Для построения боковых линий откладываем по линии талии спинки и переда соответственно Т2Т5 = 1…2 см и Т3Т6 = 0,5…1 см. Проводим боковые линии. На их пересечении с линией бёдер отмечаем (∙) Б2 и (∙) Б3. Пересечение линии бёдер со средней линией переда отмечаем (∙) Б4.
Контролируем, чтобы (Б4Б3 + Б2Б1) было больше (1/2 ОБ + 3 см). Если это не так – увеличиваем расширение деталей по линиям боков.
Из (∙) Н1 перпендикулярно средней линии спинки чертим прямую. Её пересечение с боковой линией обозначаем (∙) Н2. Из неё чертим горизонтальную прямую до пересечения с линией бока переда, ставим (∙) Н3. Проводим плавную линию низа платья.
В завершение нам нужно учесть смещение плечевой линии, чтобы получилась идеальная выкройка. Для переда плечевую линию опускаем на 1 см, для спинки – поднимаем на эту же величину.
Построение выкройки основы платья по системе Мюллера закончено.
Крой по системе 10 мерок
Выкройки, выполненные по методике, составленной Ириной Паукште, получаются очень точными, получившиеся изделия идеально сидят на фигуре.
Система кроя Паукште очень популярна среди начинающих и профессиональных закройщиков уже многие годы.
Этот простой способ построения выкройки имеет особенности:
В интернете можно найти серию уроков Ирины Паукште по построению базовой сетки, лекал спинки и полочки, расчётов к пройме.
Использование компьютерной программы для точного построения базовой выкройки
Елена Фоменкова рекомендует для построения выкройки платья использовать компьютерную программу «Валентина». Её можно бесплатно скачать в интернете.
Разберёмся с основными терминами, используемыми в программе.
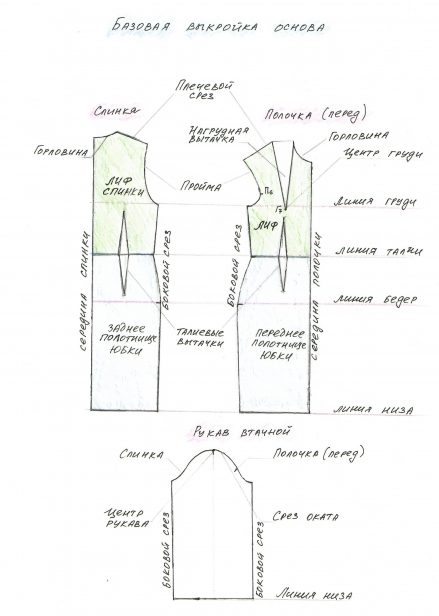
Основные конструктивные линии платья показаны на рисунке ниже.
Мерки, требуемые для построения, обозначены буквами. Полуобхваты груди, талии и бёдер – вносим в программу под буквой С. Это те замеры, которые делятся по вертикали осью симметрии.
Полные обхваты, которые нельзя делить, записываем полностью. Обозначаем их буквой О. Полностью учитываются обхваты рук, ног, щиколотки, запястья.
Остальные замеры используются полностью и обозначаются буквами Д (= длины), Ш (= ширины), В (= высоты).
Рассмотрим подробнее мерки, необходимые для построения.
Перед выполнением замеров на талии завяжем шнурок. Прибавки на свободное облегание Елена Фоменкова рекомендует давать на половину чертежа.
По этим меркам строится базовая выкройка для платья в программе «Валентина» или вручную, на листе бумаги.
Рассмотрим пошаговое построение лекала на бумаге.
Основная сетка
По краям листа проводим вертикальные прямые на расстоянии Сг 2 + Прг. Это средние линии переда и спинки. Над средней линией переда ставим точку А2. От неё по перпендикуляру влево отмеряем 25 см, найдя положение высшей точки переда.
Отмерив от точки А2 вниз Дпт, находим точку Т1. От неё влево чертим перпендикулярную линию на середину спинки, поставив на пересечении точку Т.
От этой (∙) откладываем вверх величины Дст 7 и Дст.
Ставим (∙) А6 и А. От А6 отмеряем вниз Дпл, отмечаем Н. Из неё проводим перпендикуляр на среднюю линию переда, ставим Н1. Сетка построена.
Горловина
По горизонтали из точки А откладываем 1⁄2 ширины горловины (= 1/3 Сш), ставим А3. Такую же величину откладываем на лекале переда от А2, ставим А4. От А2 вниз откладываем ширину горловины + 1,5 см. Ставим А5.
Проводим линии горловины А3А6 и А4А5.
Линия плеча переда и нагрудная вытачка
Вычисляем раствор вытачки Сг 2 – Сг 1 = h.
Из А2 отмеряем вниз Вг, отмечаем А7.
Из неё влево по перпендикуляру – Цг, точка А8. Отрезок А8А4 – первая линия вытачки. От А8 вверх откладываем h, ставим обозначение h.
В левую сторону от h отмеряем посчитанный раствор вытачки, отмечаем А9.
Из А8 через h проводим вторую линию вытачки, отмечаем А10. Из неё делаем дуговую засечку радиусом Дп + Пршп. Вторую засечку делаем радиусом Вгк из (∙) А8. На пересечении дуг отмечаем (∙) А11. Она будет низшей точкой плечевого шва. Проводим из неё линию плечевого шва до А10.
Линия плеча спинки
От точки А вниз откладываем величину, отвечающую за наклон полочки. Она равна (Вг – Вгк). Отмечаем (∙) А12. Из неё проводим вправо горизонталь длиной около 30 см. Из (∙) А3 делаем засечку радиусом (Дп + Пршсп + р-р вытачки). Р-р вытачки подсчитываем как 0,13 Дп. Результат округляем до целого числа. На месте пересечения дуги с горизонталью ставим (∙) А14. На расстоянии 3,5 см (постоянная величина для всех размеров) от А3 ставим (∙) А15. От неё отмеряем по линии раствор вытачки (= 0,13 Дп), (∙) А17.
Вниз от А15 откладываем длину вытачки. Для всех размеров она равна 9 см, ставим А16. Чертим отрезки А15А16 и А16А17. Продлеваем первый отрезок на 3 мм вверх, (∙) А18.
По прямой А16А17 откладываем отрезок равный А1А18. Завершим построение плечевого шва, соединив А3А18 и А19А14.
Пройма
От средней линии спинки откладываем 1⁄2 Шс + прибавку на свободное облегание. От линии талии отмеряем вверх Впрсп. Обозначаем (∙) пересечения А21.
На полочке аналогичную (∙) находим на пересечении Впрп и размера (Шг + Пршг). У нас есть вытачка. Поэтому отмеряем формулу на уровне h и плюсуем к результату размер (h — А9). Рисуем штрих. Снизу делаем Впрп. На пересечении – (∙) А23.
Для нахождения нижней (∙) проймы откладываем от уровня талии Впрб. Делим расстояние между вертикалями, проведёнными через А21 и А23 пополам. Точку пересечения мерки Впрб и средней вертикали обозначим А26.
Такая пройма подходит для платья без рукавов типа футляр. Для моделей с рукавами увеличиваем глубину проймы на 1…1,5 см.
Боковые швы
На пересечении перпендикуляра из А26 на низ платья ставим А30. В месте пересечения перпендикуляра с линией талии ставим А25.
От А25 отмеряем вниз Вб, ставим А31.
Найдём разницу объёма бёдер и объёма груди по формуле (Сб + Прб) – (Сг2 + Прг). Откладываем по 1⁄2 результата в обе стороны от А31. Для корректировки линии талии поднимаем её на боковых швах на 1 см, ставим А27. Рисуем линии ТА27 и А27Т1.
Вытачки на талии
Подсчитываем Вт по предложенной выше формуле. Результат распределяем между спинкой (1/2), боком (1/4) и передом (1/4).
От А27 откладываем в обе стороны по 1⁄2 вытачки.
В центре ТА28 ставим А32. От неё по вертикали в обе стороны отмеряем высоты Ввсл = А32 – А37 и Ввспб = А32 – А38.
Чертим тальевую вытачку спины А40А37А39А38.
Из А8 чертим перпендикуляр на А29Т1, точка А33. По линии опускаемся на 2 см (для всех размеров), точка А34. От линии Т1А29 на расстоянии Ввпб продлеваем А8А33, точка А41.
От А33 в обе стороны отмеряем 1⁄2 вытачки переда, получим А35 и А36. Строим вытачку переда А41А35А34А36. Проводим боковой шов спины А26А28А43А45 и переда А26А29А42А44. Базовая выкройка построена.
Дополнительно построение можно посмотреть по видео.
Пример построения выкройки трикотажного платья
Чтобы построить выкройку воспользуемся европейской системой кроя, рекомендованной сайтом «Швейных дел мастер».
Выкройка платья из эластичных тканей имеет упрощённый вид, поскольку в ней отсутствуют вытачки.
Снимаем мерки, как описано для предыдущей методики.
Особенность трикотажных тканей растягиваться в продольном и поперечном направлениях мы учтём отрицательной прибавкой на свободное облегание. Для правильной посадки изделия прибавка на полуобхват груди будет минус 2 см. Разделим их поровну на спинку и перёд.
Поскольку способ построения лекала подобен предыдущей методике, ограничимся формулами для вычислений и пошаговыми чертежами.
Спинка
АГ = Впрз + прибавка.
Ат = Дст 2 + прибавка.
ТБ = 18 см (для всех размеров).
АА1 = 2,5 см (для всех размеров).
ГГ2 = 1⁄2 (Сг 2 + 1⁄2 Пр).
П2П3 = 1,2 см (для всех р-ров).
Перёд
Г3Г5 = 1⁄2 (Сг 2 + 1⁄2 Пр).
От Н2 вниз отмеряем 1 см.
Пример построения базовой выкройки платья приталенного силуэта
Для наглядности воспользуемся чертежами сайта «Шей со мной».
Снимаем мерки. Обозначения замеров на сайте «Шей со мной» совпадают с обозначениями в наших предыдущих описаниях, поэтому вам будет не сложно разобраться.
Аналогично предыдущему описанию, мы ограничимся формулами и поэтапными чертежами.
Откладываем высотные размеры:
Ширину спинки и переда на сайте «Шей со мной» подсчитывают по формулам:
Спинка
*А2А21 = 1/3 АА2 + Пвгс.
Наклон плеча на сайте «Шей со мной» находится с помощью двух радиусов:
*R1 = А2П1 = Шп + 1,5 см (вытачка) + 0,5 см;
От А2 отмеряем 4 см (для всех р-ров), вниз – 12 см. Раствор вытачки – 1,5 см. На сайте «Шей со мной» подчёркивается, что длина сторон вытачки должна быть равной.
Если вытачка при дальнейшем моделировании будет переводиться в бок, то удлиняем её до линии лопаток.
Далее строим пройму – см. чертёж.
Перёд
Опускаем линию талии:
Наклон плеча построим, используя два радиуса:
*Г6П5 = Впкп + 1⁄2 Пдтп.
Построение проймы – см. на чертеже выше.
Проверим ширину переда на линии через П6.
Проверяем построением этот размер. Намечаем вход в карман.
Делаем равную длину отрезков Г’Г4 = Б’Б21.
Расширяем бёдра на величину (Сб + Пб) – Г’Г1, отложив её равные части в каждую сторону.

Общий размер вытачек — Т’Т1 – (Ст + Пт) делим на четыре части:
Оформляем линию низа.
Готовые выкройки платья приталенного силуэта
Для начинающих мы предлагаем готовые выкройки платьев.
Вам нужно снять мерки и сравнить их с приведёнными ниже (в скобках приведены российские размеры):










В завершение нужно отметить, что на основе базовой выкройки, построенной по любой из методик, можно выполнить моделирование платьев самых разных фасонов.