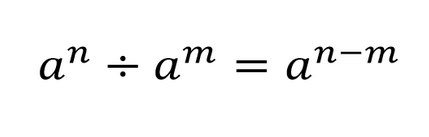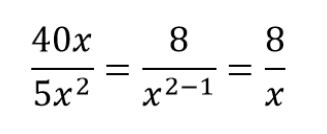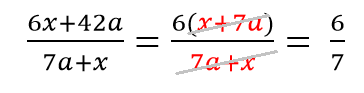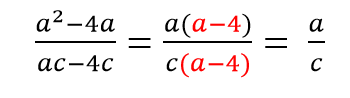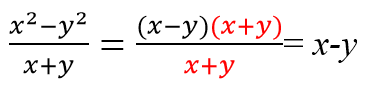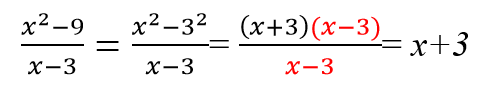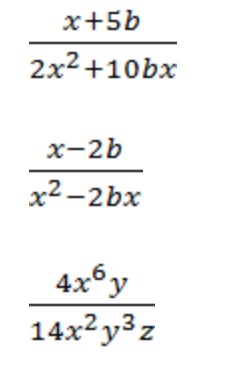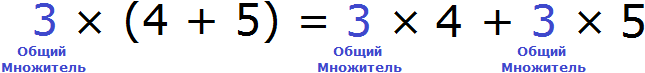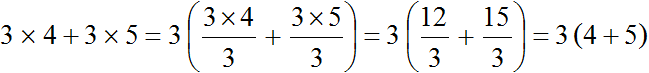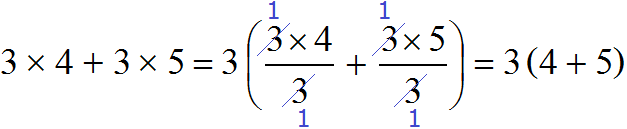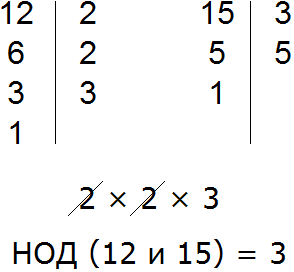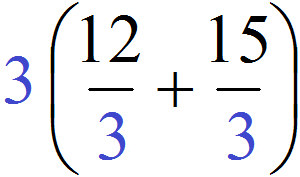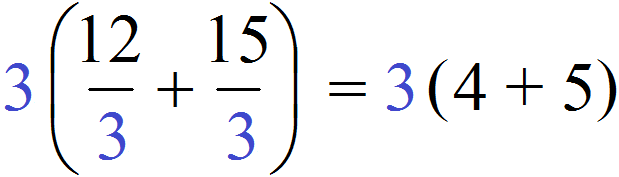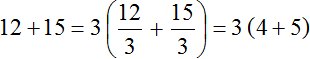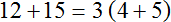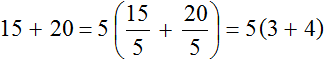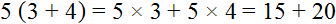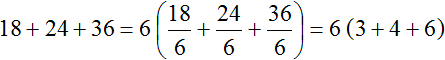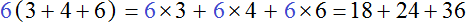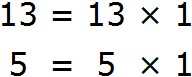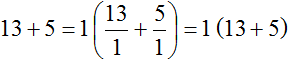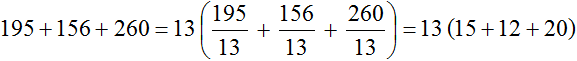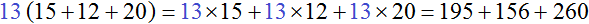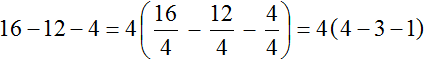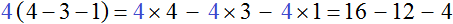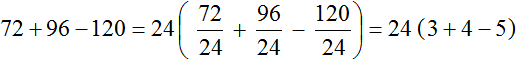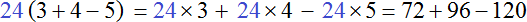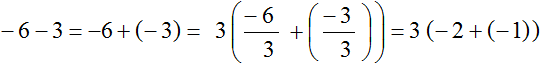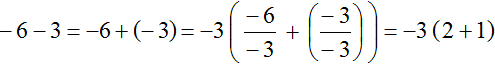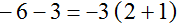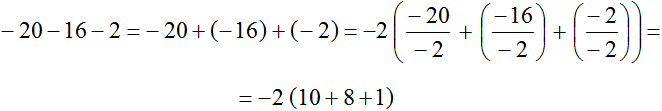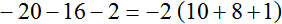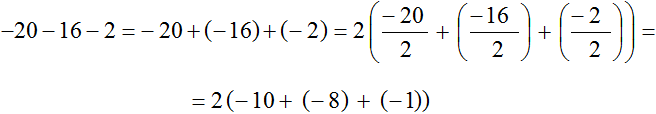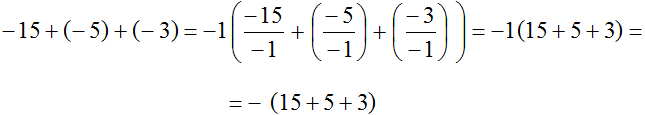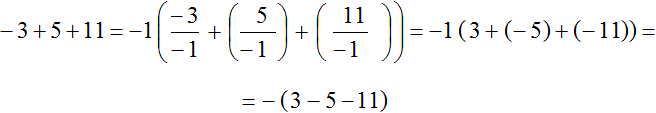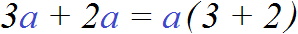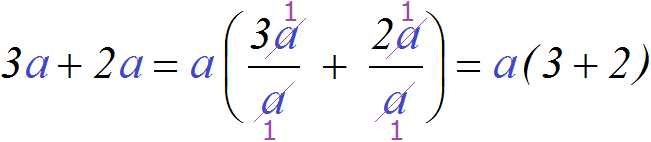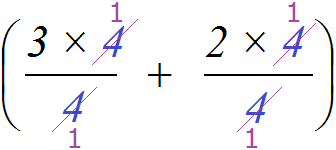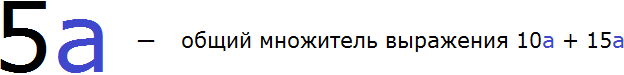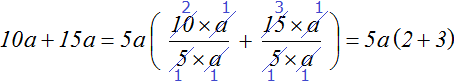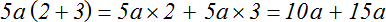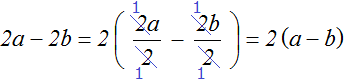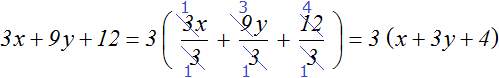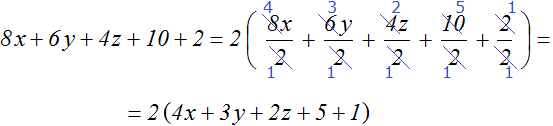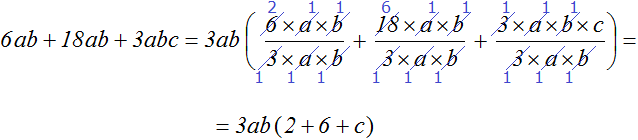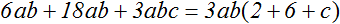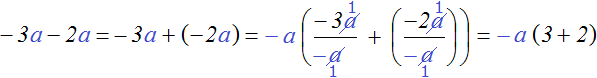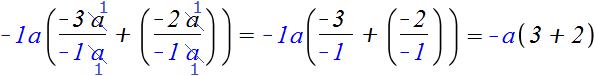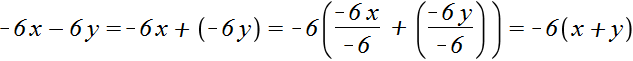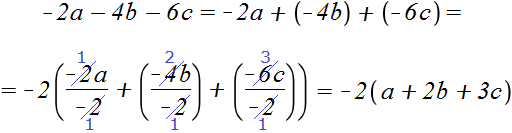Как вынести за скобку дробь
Вынесение общего множителя за скобку
Вынесение общего множителя – один из основных способов разложения на множители. По сути является действием обратным раскрытию скобок.
Главное правило вынесения за скобку:
Выносить за скобку можно только те множители, которые есть во всех слагаемых (одночленах).
К примеру, в выражении \(3ab+5bc-abc\) за скобку можно вынести только \(b\), потому что лишь оно есть во всех трех слагаемых. Процесс вынесения общих множителей за скобку представлен на схеме ниже:
Правила вынесения за скобки
В математике принято выносить сразу все общие множители.
Пример: \(3xy-3xz=3x(y-z)\)
Обратите внимание, здесь мы могли бы разложить и вот так: \(3(xy-xz)\) или так: \(x(3y-3z)\). Однако это были бы неполные разложения. Выносить надо и тройку, и икс.
Иногда общие члены сразу не видны.
Пример: \(10x-15y=2·5·x-3·5·y=5(2x-3y)\)
В этом случае общий член (пятерка) была скрыта. Однако разложив \(10\) как \(2\) умножить на \(5\), а \(15\) как \(3\) умножить на \(5\) – мы «вытащили пятерку на свет Божий», после чего легко смогли вынести ее за скобку.
Если одночлен выносится полностью – от него остается единица.
Пример: \(5xy+axy-x=x(5y+ay-1)\)
Мы за скобку выносим \(x\), а третий одночлен и состоит только из икса. Почему же от него остается единица? Потому что если любое выражение умножить на единицу – оно не изменится. То есть этот самый \(x\) можно представить как \(1\cdot x\). Тогда имеем следующую цепочку преобразований:
Более того – это единственно правильный способ вынесения, потому что если мы единицу не оставим, то при раскрытии скобок мы не вернемся к исходному выражению. Действительно, если сделать вынесение вот так \(5xy+axy-x=x(5y+ay)\), то при раскрытии мы получим \(x(5y+ay)=5xy+axy\). Третий член – пропал. Значит, такое вынесение некорректно.
За скобку можно выносить знак «минус», при этом знаки членов с скобке меняются на противоположные.
Пример: \(x-y=-(-x+y)=-(y-x)\)
По сути здесь мы выносим за скобку «минус единицу», которая может быть «выделена» перед любым одночленом, даже если минуса перед ним не было. Мы здесь используем тот факт, что единицу можно записать как \((-1) \cdot (-1)\). Вот тот же пример, расписанный подробно:
Скобка тоже может быть общим множителем.
Таким образом, получаем:
Как сократить дробь
Как сократить алгебраическую (рациональную) дробь, числитель и знаменатель которой содержат выражения, которые отличаются только знаками?
Например, как сократить дробь
Для начала вспомним, как от выражения (a-b) перейти к выражению (b-a). Для этого нужно вынести «минус» за скобки (при этом все знаки слагаемых в скобках изменятся на противоположные):
В дроби вынести «минус» за скобки можно или в числителе, или в знаменателе. По свойству алгебраических дробей, знак «минус» можно вынести перед дробью:
В данном примере числитель и знаменатель дроби сокращаем на (a-b):
Рассмотрим другие примеры сокращения алгебраических дробей такого вида.
Сокращать можно только множители!
В числителе и знаменателе дроби — многочлены. Чтобы сократить дробь, надо разложить многочлены на множители. В числителе есть общий множитель 2b, в знаменателе — a. Вынесем их за скобки:
Выражения, стоящие в скобках в числителе и в знаменателе, отличаются только знаками. Вынесем знак «минус» перед дробью, например, из знаменателя (при этом все знаки слагаемых, стоящих в скобках, изменятся на противоположные):
После чего сокращаем дробь на общий делитель (2a-b).
В числителе выносим общий множитель 2 за скобки, знаменатель раскладываем по формуле разности квадратов:
Вынесем «минус» перед дробью, например, из числителя:
Сокращаем дробь на (m-7).
В числителе — 4 слагаемых. Группируем первое слагаемое со вторым, третье — с четвертым. В знаменателе выносим общий множитель 6 за скобки:
Сокращаем дробь на (x-3):
То есть, чтобы сменить знаки слагаемых в квадрате разности, «минус» за скобки (и перед дробью) выносить не нужно. Это верно не только для квадрата разности, но и для любой другой четной степени:
В случае возведения разности в нечетную степень при смене знаков слагаемых знак «минус» за скобки выносить нужно:
В числителе — полный квадрат разности, в знаменателе — разность квадратов. Раскладываем на множители:
Удобнее изменить знаки слагаемых вверху, поскольку при этом не нужно изменять знак перед дробью:
Сокращаем дробь на (10y-9x):
Вынесем знак «минус» перед дробью, например, из знаменателя:
Сокращение дробей в алгебре — важная составляющая часть сложения, вычитания, умножения и деления алгебраических дробей. Упрощать рациональные выражения приходится при решении уравнений, неравенств, задач и т.д.
Далее мы будем рассматривать действия над алгебраическими дробями.
Вынесение общего множителя за скобки
Разложить многочлен на множители можно несколькими способами. Один из них называется вынесение общего множителя за скобки.
Разложить многочлен на множители — значит представить его в виде произведения двух и более многочленов.
Как вынести общий множитель за скобки
Чтобы вынести общий множитель за скобки нужно выполнить следующие действия.
Рассмотрим пример вынесения общего множителя за скобки.
Сначала определим число, на которое без остатка делятся все числовые коэффициенты одночленов. Для этого выпишем все числовые коэффициенты в таблицу ниже.
| Одночлен | Числовой коэффициент | Вывод |
|---|---|---|
| 6a 2 | 6 | Все числовые коэффициенты делятся без остатка на число « 3 ». |
| −3a | −3 | |
| 12ab | 12 |
Определим буквенные множители, которые повторяются во всех одночленах.
В многочлене « 6a 2 − 3a + 12ab » — только буквенный множитель « a » присутствует во всех одночленах. Наименьшая степень буквенного множителя « a » среди всех одночленов — первая.
Теперь перемножим выбранный числовой коэффициент и буквенный множитель.
Получим « 3a » и вынесем его за скобки.
Теперь вычислим оставшийся многочлен в скобках. Для этого составим таблицу ниже, где будем к каждому одночлену задавать вопрос:
«На что нужно умножить « 3а », чтобы получить данный одночлен?»
| Вопрос | Полученный одночлен |
|---|---|
| На что нужно умножить « 3а », чтобы получить « 6а 2 »? | На « 2а ». |
| На что нужно умножить « 3а », чтобы получить « −3a »? | На « −1 ». |
| На что нужно умножить « 3а », чтобы получить « 12ab »? | На « 4b ». |
Запишем полученный ответ.
Всегда проверяйте полученный результат вынесения общего множителя.
Для этого раскройте скобки в полученном результате по правилу умножения многочлена на одночлен.
Если вы вынесли общий множитель правильно, то вы должны получить исходный многочлен.
Проверим, правильно ли мы вынесли общий множитель за скобки.
При раскрытии скобок мы получили исходный многочлен, значит мы правильно вынесли общий множитель за скобки.
Действие обратное вынесению общего множителя за скобки называется раскрытием скобок.
Примеры вынесения общего множителя за скобки
Вынесение общего многочлена за скобки
Иногда есть возможность вынести многочлен за скобки целиком.
В таком случае оставшиеся одночлены просто записываются в скобки друг за другом вместе со знаком, который стоял слева от них.
Как сокращать алгебраические дроби?
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:
Алгебраическая дробь содержит буквенные множители и степени.
Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.
Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.
Сокращение алгебраических дробей
Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.
Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.
Сокращение дробей с буквами и степенями проходит в три этапа:
Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:
Пример сокращения дроби со степенями и буквами:
Получаем сокращенную дробь.
Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.
| ❌ Так нельзя | ✅ Так можно |
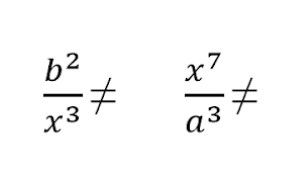 |  |
Примеры сокращения алгебраических дробей с одночленами:
Пример сокращения №1.
Получаем сокращенную алгебраическую дробь.
Пример сокращения №2.
Получаем сокращенную дробь.
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Сокращение алгебраических дробей с многочленами
Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:
Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.
Примеры сокращения алгебраических дробей с многочленами:
Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).
Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.
Вынесение общего множителя при сокращении дробей
При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.
Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:
Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.
| Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен. |
Пример 1.
Пример 2.
Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.
Сокращение дробей. Формулы сокращенного умножения
Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.
Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.
Примеры сокращения дробей с помощью формул сокращенного умножения:
Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.
Примеры сокращения дробей за 7 и 8 классы
Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.
Вынесение общего множителя за скобки
Основной принцип
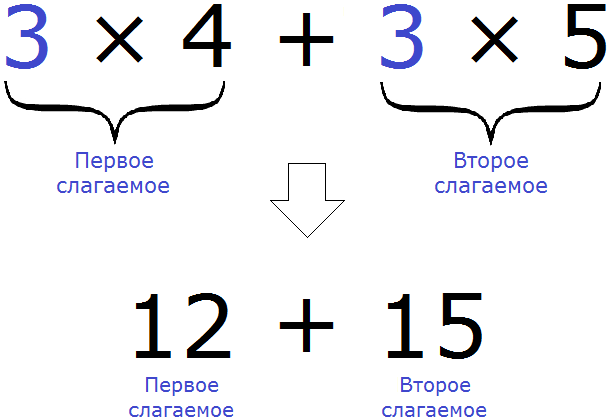
Распределительный закон умножения позволяет умножить число на сумму (или сумму на число). Например, чтобы найти значение выражения 3 × (4 + 5) можно умножить число 3 на каждое слагаемое в скобках и сложить полученные результаты:
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
Число 3 и выражение в скобках можно поменять местами (это следует из переместительного закона умножения). Тогда каждое слагаемое, которое в скобках, будет умножено на число 3
(4 + 5) × 3 = 4 × 3 + 5 × 3 = 12 + 15
Распределительный закон умножения иногда называют внесением множителя во внутрь скобок. В выражении 3 × (4 + 5) множитель 3 был за скобками. Умножив его на каждое слагаемое в скобках, мы по сути внесли его во внутрь скобок. Для наглядности можно так и записать, хоть и не принято так записывать:
3 (4 + 5) = ( 3 × 4 + 3 × 5)
Поскольку в выражении 3 × (4 + 5) число 3 умножается на каждое слагаемое в скобках, это число является общим множителем для слагаемых 4 и 5
3 (4 + 5) = 3 × 4 + 3 × 5
Если вычислить обе части полученного равенства, то получим тождество:
3 (4 + 5) = 3 × 4 + 3 × 5
Как происходит вынесение общего множителя за скобки
Вынесение общего множителя за скобки по сути является обратной операцией внесению общего множителя во внутрь скобок.
Если при внесении общего множителя внутрь скобок, мы умножаем этот множитель на каждое слагаемое в скобках, то при вынесении этого множителя обратно за скобки, мы должны разделить каждое слагаемое в скобках на этот множитель.
Теперь мы можем детально увидеть, как происходит вынесение общего множителя за скобки:
Видно, что общий множитель 3 сначала вынесен за скобки, затем в скобках происходит деление каждого слагаемого на этот общий множитель.
Деление каждого слагаемого на общий множитель можно выполнять не только разделяя числитель на знаменатель, как это было показано выше, но и сокращая эти дроби. В обоих случаях получится один и тот же результат:
Мы рассмотрели простейший пример вынесения общего множителя за скобки, чтобы понять основной принцип.
Но не всё так просто, как кажется на первый взгляд. После того, как число умножено на каждое слагаемое в скобках, полученные результаты складывают, и общий множитель пропадает из виду.
3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15
Обычно при решении задач встречаются именно такие выражения, в которых общий множитель сначала нужно найти, прежде чем его выносить.
Чтобы в выражении 12 + 15 вынести общий множитель за скобки, нужно найти наибольший общий делитель (НОД) слагаемых 12 и 15. Найденный НОД и будет общим множителем.
Итак, найдём НОД слагаемых 12 и 15. Напомним, что для нахождения НОД необходимо разложить исходные числа на простые множители, затем выписать первое разложение и убрать из него множители, которые не входят в разложение второго числа. Оставшиеся множители нужно перемножить и получить искомый НОД. Если испытываете затруднения на этом моменте, обязательно повторите этот урок.
НОД слагаемых 12 и 15 это число 3. Данное число является общим множителем слагаемых 12 и 15. Его и нужно выносить за скобки. Для этого сначала записываем сам множитель 3 и рядом в скобках записываем новое выражение, в котором каждое слагаемое выражения 12 + 15 разделено на общий множитель 3
Ну и дальнейшее вычисление не составляет особого труда. Выражение в скобках легко вычисляется — двенадцать разделить на три будет четыре, а пятнадцать разделить на три будет пять:
В коротком решении пропускают запись в которой показано, как каждое слагаемое разделено на общий множитель:
Пример 2. Вынести общий множитель за скобки в выражении 15 + 20
Наибольший общий делитель слагаемых 15 и 20 это число 5. Данное число является общим множителем слагаемых 15 и 20. Его и вынесем за скобки:
Получили выражение 5(3 + 4).
Получившееся выражение 5(3 + 4) можно проверить. Для этого достаточно умножить пятёрку на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 15 + 20
Пример 3. Вынести общий множитель за скобки в выражении 18 + 24 + 36
Найдём НОД слагаемых 18, 24 и 36. Чтобы найти НОД нескольких чисел, нужно разложить эти числа на простые множители, затем найти произведение общих множителей:
НОД слагаемых 18, 24 и 36 это число 6. Данное число является общим множителем слагаемых 18, 24 и 36. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим число 6 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 18 + 24 + 36
Пример 4. Вынести общий множитель за скобки в выражении 13 + 5
Слагаемые 13 и 5 являются простыми числами. Они раскладываются только на единицу и самих себя:
Это значит, что у слагаемых 13 и 5 нет общих множителей, кроме единицы. Соответственно, нет смысла выносить эту единицу за скобки, поскольку это ничего не даст. Покажем это:
Пример 5. Вынести общий множитель за скобки в выражении 195 + 156 + 260
Найдём НОД слагаемых 195, 156 и 260
НОД слагаемых 195, 156 и 260 это число 13. Данное число является общим множителем для слагаемых 195, 156 и 260. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим 13 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 195 + 156 + 260
Выражение, в котором требуется вынести общий множитель за скобки, может быть не только суммой чисел, но и разностью. Например, вынесем общий множитель за скобки в выражении 16 − 12 − 4. Наибольшим общим делителем чисел 16, 12 и 4 это число 4. Данное число и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим четвёрку на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 16 − 12 − 4
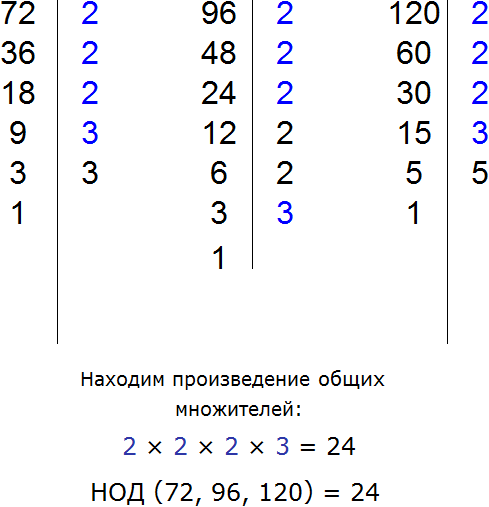
Пример 6. Вынести общий множитель за скобки в выражении 72 + 96 − 120
Найдём НОД чисел 72, 96 и 120
НОД для 72, 96 и 120 это число 24. Данное число является общим множителем слагаемых 195, 156 и 260. Его и вынесем за скобки:
Проверим получившееся выражение. Для этого умножим 24 на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 72+96−120
Общий множитель, выносимый за скобки, может быть и отрицательным. Например, вынесем общий множитель за скобки в выражении −6 − 3. Вынести общий множитель за скобки в таком выражении можно двумя способами. Рассмотрим каждый из них.
Способ 1.
Заменим вычитание сложением:
Теперь находим общий множитель. Общим множителем данного выражения будет наибольший общий делитель модулей слагаемых −6 и −3.
Модуль первого слагаемого это 6. А модуль второго слагаемого это 3. НОД(6 и 3) равен 3. Данное число является общим множителем слагаемых 6 и 3. Его и вынесем за скобки:
Выражение полученное таким способом получилось не очень аккуратным. Много скобок и отрицательных чисел не придают выражению простоту. Поэтому можно воспользоваться вторым способом, суть которого заключается в том, чтобы вынести за скобки не 3, а −3.
Способ 2.
Как и в прошлый раз заменяем вычитание сложением
В этот раз мы вынесем за скобки не 3, а −3
Выражение полученное в этот раз выглядит намного проще. Запишем решение покороче, чтобы сделать его ещё проще:
Разрешать выносить отрицательный множитель за скобки связано с тем, что разложение чисел −6 и (−3) можно записать двумя видами: сначала сделать множимое отрицательным, а множитель положительным:
во втором случае множимое можно сделать положительным, а множитель отрицательным:
А значит мы вольны выносить за скобки тот сомножитель, который захотим.
Пример 8. Вынести общий множитель за скобки в выражении −20 − 16 − 2
Заменим вычитание сложением
−20 − 16 − 2 = −20 + (−16) + (−2)
Наибольшим общим делителем слагаемых −20, −16 и −2 является число 2. Это число является общим множителем этих слагаемых. Посмотрим, как это выглядит:
Запишем приведенное решение покороче:
Пример 9. Вынести общий множитель за скобки в выражении −30 − 36 − 42
Заменим вычитание сложением:
Наибольшим общим делителем слагаемых −30, −36 и −42 это число 6. Данное число является общим множителем для этих слагаемых. Но за скобки мы вынесем не 6, а −6 поскольку числа −30, −36 и −42 можно представить так:
Вынесение минуса за скобки
При решении задач иногда может быть полезным вынесение минуса за скобки. Это позволяет упростить выражение и сделать его проще.
Рассмотрим следующий пример. Вынести минус за скобки в выражении −15 + (−5) + (−3)
Для наглядности заключим данное выражение в скобки, ведь речь идёт о том, чтобы вынести минус за эти скобки
Итак, чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые, но с противоположными знаками. Знаки операций (то есть плюсы) оставляем без изменений:
Поэтому между выражениями −15 + (−5) + (−3) и −(15 + 5 + 3) можно поставить знак равенства, потому что они равны одному и тому же значению:
−15 + (−5) + (−3) = −(15 + 5 + 3)
На самом деле при вынесении минуса за скобки опять же срабатывает распределительный закон умножения:
Если поменять местами левую и правую часть этого тождества, то получится, что сомножитель a вынесен за скобки
Тоже самое происходит, когда мы выносим общий множитель в других выражениях и когда выносим минус за скобки.
Очевидно, что при вынесении минуса за скобки, выносится не минус, а минус единица. Ранее мы говорили, что коэффициент 1 принято не записывать.
Поэтому и образуется перед скобками минус, а знаки слагаемых которые были в скобках меняют свой знак на противоположный, поскольку каждое слагаемое разделено на минус единицу.
Вернёмся к предыдущему примеру и детально увидим, как на самом деле выносился минус за скобки
Пример 2. Вынести минус за скобки в выражении −3 + 5 + 11
Ставим минус и рядом в скобках записываем выражение −3 + 5 + 11 с противоположным знаком у каждого слагаемого:
−3 + 5 + 11 = −(3 − 5 − 11)
Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица. Подробное решение выглядит следующим образом:
Вынесение общего множителя за скобки в буквенном выражении
Выносить общий множитель за скобки в буквенном выражении намного интереснее.
Как и в случае с числовым выражением, здесь происходит деление каждого слагаемого на вынесенный общий множитель. Выглядит это так:
Например, если вместо переменной a подставить число 4, то конструкция 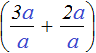
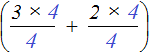
Поэтому не следует пугаться при виде сокращения переменных. Переменная это полноправный множитель, пусть даже выраженный буквой. Такой множитель можно выносить за скобки, сокращать и выполнять другие действия, которые допустимы к обычным числам.
Буквенное выражение содержит не только числа, но и буквы (переменные). Поэтому общий множитель, который выносится за скобки часто бывает буквенным множителем, состоящим из числа и буквы (коэффициента и переменной). К примеру, следующие выражения являются буквенными множителями:
Прежде чем выносить такой множитель за скобки, нужно определиться, какое число будет в числовой части общего множителя и какая переменная будет в буквенной части общего множителя. Другими словами, нужно узнать какой коэффициент будет у общего множителя и какая переменная будет в него входить.
Проверим получившееся выражение. Для этого умножим 5a на каждое слагаемое в скобках. Если мы всё сделали правильно, то получим выражение 10a + 15a
Буквенный множитель не всегда можно вынести за скобки. Иногда общий множитель состоит только из числа, поскольку ничего подходящего для буквенной части в выражении не находится.
Пример 2. Вынести общий множитель выражении 3x + 9y + 12
Коэффициентами данного выражения являются числа 3, 9 и 12, их НОД равен 3. Значит коэффициентом общего множителя, выносимого за скобки, будет число 3. А среди буквенных сомножителей (переменных) нет общего множителя. Поэтому окончательный общий множитель это 3
Пример 3. Вынести общий множитель за скобки в выражении 8x + 6y + 4z + 10 + 2
Коэффициентами данного выражения являются числа 8, 6, 4, 10 и 2, их НОД равен 2. Значит коэффициентом общего множителя, выносимого за скобки, будет число 2. А среди буквенных сомножителей нет общего множителя. Поэтому окончательный общий множитель это 2
Пример 4. Вынести общий множитель 6ab + 18ab + 3abc
Коэффициентами данного выражения являются числа 6, 18 и 3, их НОД равен 3. Значит коэффициентом общего множителя, выносимого за скобки, будет число 3. В буквенную часть общего множителя будут входить переменные a и b, поскольку в выражении 6ab + 18ab + 3abc эти две переменные входят в каждое слагаемое. Поэтому окончательный общий множитель это 3ab
При подробном решении выражение становится громоздким и даже непонятным. В данном примере это более чем заметно. Это связано с тем, что мы сокращаем множители в числителе и в знаменателе. Лучше всего делать это в уме и сразу записывать результаты деления. Тогда выражение станет коротким и аккуратным:
Как и в случае с числовым выражением в буквенном выражении общий множитель может быть и отрицательным.
Для удобства заменим вычитание сложением
−3 a − 2 a = −3 a + (−2 a )
Пример 6. Вынести общий множитель за скобки в выражении −6x − 6y
Заменим вычитание сложением
Вынесем за скобки −6
Запишем решение покороче:
Пример 7. Вынести общий множитель за скобки в выражении −2a − 4b − 6c
Заменим вычитание сложением
Вынесем за скобки −2
Запишем решение покороче:
−2a − 4b − 6c = −2(a + 2b + 3c)
Вынесение общего множителя за скобки это очень важная тема. В данном уроке рассмотрены только азы и простейшие примеры. Мы ещё вернемся к этой теме, когда будем изучать многочлены.
Обязательно изучите данный урок, поскольку при изучении многочленов потребуется выносить за скобки сложный множитель, состоящий из степеней.