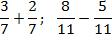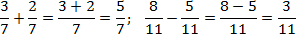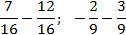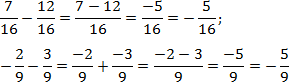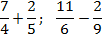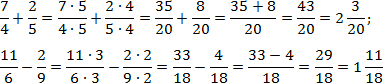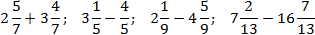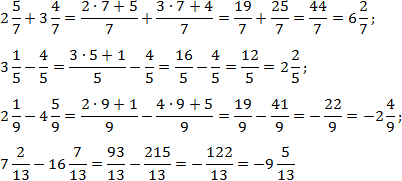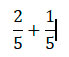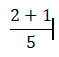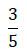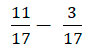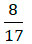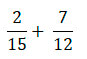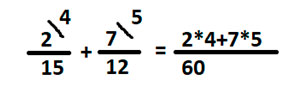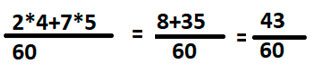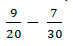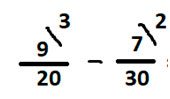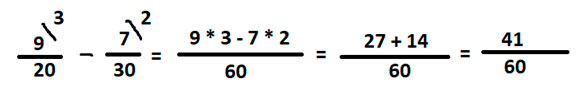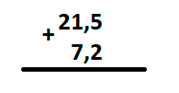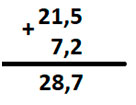Как выполнить сложение и вычитание дробей
Сложение и вычитание дробей
Дроби — это обычные числа, их тоже можно складывать и вычитать. Но из-за того, что в них присутствует знаменатель, здесь требуются более сложные правила, нежели для целых чисел.
Рассмотрим самый простой случай, когда есть две дроби с одинаковыми знаменателями. Тогда:
Чтобы с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить без изменений.
Чтобы с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель опять же оставить без изменений.
Задача. Найдите значение выражения:
Внутри каждого выражения знаменатели дробей равны. По определению сложения и вычитания дробей получаем:
Как видите, ничего сложного: просто складываем или вычитаем числители — и все.
Но даже в таких простых действиях люди умудряются допускать ошибки. Чаще всего забывают, что знаменатель не меняется. Например, при сложении их тоже начинают складывать, а это в корне неправильно.
Избавиться от вредной привычки складывать знаменатели достаточно просто. Попробуйте сделать то же самое при вычитании. В результате в знаменателе получится ноль, и дробь (внезапно!) потеряет смысл.
Поэтому запомните раз и навсегда: при сложении и вычитании знаменатель не меняется!
Также многие допускают ошибки при сложении нескольких отрицательных дробей. Возникает путаница со знаками: где ставить минус, а где — плюс.
Эта проблема тоже решается очень просто. Достаточно вспомнить, что минус перед знаком дроби всегда можно перенести в числитель — и наоборот. Ну и конечно, не забывайте два простых правила:
Разберем все это на конкретных примерах:
Задача. Найдите значение выражения:
В первом случае все просто, а во втором внесем минусы в числители дробей:
Что делать, если знаменатели разные
Напрямую складывать дроби с разными знаменателями нельзя. По крайней мере, мне такой способ неизвестен. Однако исходные дроби всегда можно переписать так, чтобы знаменатели стали одинаковыми.
Существует много способов преобразования дробей. Три из них рассмотрены в уроке «Приведение дробей к общему знаменателю», поэтому здесь мы не будем на них останавливаться. Лучше посмотрим на примеры:
Задача. Найдите значение выражения:
В первом случае приведем дроби к общему знаменателю методом «крест-накрест». Во втором будем искать НОК. Заметим, что 6 = 2 · 3; 9 = 3 · 3. Последние множители в этих разложениях равны, а первые взаимно просты. Следовательно, НОК(6; 9) = 2 · 3 · 3 = 18.
Что делать, если у дроби есть целая часть
Могу вас обрадовать: разные знаменатели у дробей — это еще не самое большое зло. Гораздо больше ошибок возникает тогда, когда в дробях-слагаемых выделена целая часть.
Безусловно, для таких дробей существуют собственные алгоритмы сложения и вычитания, но они довольно сложны и требуют долгого изучения. Лучше используйте простую схему, приведенную ниже:
Правила перехода к неправильным дробям и выделения целой части подробно описаны в уроке «Что такое числовая дробь». Если не помните — обязательно повторите. Примеры:
Задача. Найдите значение выражения:
Здесь все просто. Знаменатели внутри каждого выражения равны, поэтому остается перевести все дроби в неправильные и сосчитать. Имеем:
Чтобы упростить выкладки, я пропустил некоторые очевидные шаги в последних примерах.
Небольшое замечание к двум последним примерам, где вычитаются дроби с выделенной целой частью. Минус перед второй дробью означает, что вычитается именно вся дробь, а не только ее целая часть.
Перечитайте это предложение еще раз, взгляните на примеры — и задумайтесь. Именно здесь начинающие допускают огромное количество ошибок. Такие задачи обожают давать на контрольных работах. Вы также неоднократно встретитесь с ними в тестах к этому уроку, которые будут опубликованы в ближайшее время.
Резюме: общая схема вычислений
В заключение приведу общий алгоритм, который поможет найти сумму или разность двух и более дробей:
Помните, что выделять целую часть лучше в самом конце задачи, непосредственно перед записью ответа.
Сложение дробей: теория и практика
Понятие дроби
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Существует два формата записи:
Над чертой принято писать делимое, которое является числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между ними означает деление.
Дроби бывают двух видов:
Числовые — состоят из чисел, например, 5/9 или (1,5 − 0,2)/15.
Алгебраические — состоят из переменных, например, (x + y)/(x − y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной называют такую дробь, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как пять целых одна четвертая, а записывается — 5 1/4.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!
Как плюсовать дроби
Сложение — это арифметическое действие, в результате которого получается новое число. Оно содержит в себе сумму заданных чисел.
Свойства сложения
Давайте рассмотрим несколько вариантов сложения обыкновенных дробей.
Сложение дробей с одинаковыми знаменателями
Чтобы получить сумму двух дробей с равными знаменателями, нужно сложить числители исходных дробей, а знаменатель оставить прежним.
Не забудьте проверить, можно ли сократить дробь.
Сложение дробей с разными знаменателями
Как складывать дроби с разными знаменателями — для этого нужно найти наименьший общий знаменатель (далее — НОЗ), а затем воспользоваться предыдущим правилом. Вот, что делать:
1. Найдем наименьшее общее кратное знаменателей (далее — НОК) для определения единого делителя.
Для этого записываем в столбик числа, которые в произведении дают значения знаменателей складываемых дробей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 × 2 × 3 × 5 = 90
2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
Полученные числа записываем справа сверху над числителем.
3. Воспользуемся одним из основных свойств дробей: перемножим делимое и делитель на дополнительный множитель. После умножения делитель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
4. Проверим полученный результат:
Еще раз ход решения одной строкой:
Сложение смешанных чисел
Сложение смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
1. Сложить целые части.
2. Сложить дробные части.
Если знаменатели разные, воспользуемся знаниями из предыдущего примера и приведем к общему.
3. Суммируем полученные результаты.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Прибавление и вычитание дробей — смежные темы: принципы и закономерности очень похожи. Чтобы закрепить знания, тренируйтесь решать примеры на сложение дробей как можно чаще.
Обыкновенные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доля целого
Доля — это каждая равная часть, из суммы которых состоит целый предмет.
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Чтобы быстрее запомнить соотношения частей и целого, можно использовать наглядную табличку:
Понятие дроби
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
Виды дробей:
Какие еще бывают дроби:
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3\5.
Выделение целой части из неправильной дроби — это запись неправильной дроби в виде суммы натурального числа и правильной дроби. Например, 11/5 = 2 + 1/5.
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
Чтобы привести дроби к наименьшему общему знаменателю, нужно:
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
В этом примере делим обе части дроби на двойку.
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
Полученные числа запишем справа сверху над числителем.
Ход решения одной строкой:
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
Не забываем про сокращение. Это может облегчить вычисления.
Чтобы умножить два смешанных числа, надо:
Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
Сложение и вычитание алгебраических дробей: правила, примеры
Данная статья начинает изучение действий с алгебраическими дробями: рассмотрим подробно такие действия как сложение и вычитание алгебраических дробей. Разберем схему сложения и вычитания алгебраических дробей как с одинаковыми знаменателями, так и с разными. Изучим, как сложить алгебраическую дробь с многочленом и как произвести их вычитание. На конкретных примерах поясним каждый шаг поиска решения задач.
Действия сложения и вычитания при одинаковых знаменателях
Схема сложения обыкновенных дробей применима и для алгебраических. Мы знаем, что при сложении или вычитании обыкновенных дробей с одинаковыми знаменателями необходимо сложить или вычесть их числители, а знаменатель остается исходным.
Соответственно аналогичным образом записывается правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями:
Чтобы осуществить сложение или вычитание алгебраических дробей с одинаковыми знаменателями, нужно соответственно сложить или вычесть числители исходных дробей, а знаменатель записать без изменений.
Укажем пример применения сформулированного правила.
Решение
Исходные дроби содержат одинаковые знаменатели. Согласно правилу, выполним сложение числителей заданных дробей, а знаменатель оставим неизменным.
В практике, как во многих случаях, решение приводится цепочкой равенств, наглядно показывающей все этапы решения:
Результатом сложения или вычитания может стать сократимая дробь, в этом случае оптимально ее сократить.
Решение
Знаменатели исходных дробей равны. Произведем действия с числителями, а именно: вычтем из числителя первой дроби числитель второй, после чего запишем результат, оставляя знаменатель неизменным:
Мы видим, что полученная дробь – сократимая. Осуществим ее сокращение, преобразовав знаменатель при помощи формулы разности квадратов:
По такому же принципу складываются или вычитаются три и более алгебраических дробей при одинаковых знаменателях. К примеру:
Действия сложения и вычитания при разных знаменателях
Вновь обратимся к схеме действий с обыкновенными дробями: чтобы выполнить сложение или вычитание обыкновенных дробей с разными знаменателями, необходимо привести их к общему знаменателю, а затем сложить полученные дроби с одинаковыми знаменателями.
Так же по аналогии сформулируем правило сложения и вычитания алгебраических дробей с разными знаменателями:
Чтобы осуществить сложение или вычитание алгебраических дробей с разными знаменателями, необходимо:
Очевидно, что ключевым здесь будет навык приведения алгебраических дробей к общему знаменателю. Разберем подробнее.
Приведение алгебраических дробей к общему знаменателю
Чтобы привести алгебраические дроби к общему знаменателю, необходимо осуществить тождественное преобразование заданных дробей, в результате которого знаменатели исходных дробей становятся одинаковыми. Здесь оптимально действовать по следующему алгоритму приведения алгебраических дробей к общему знаменателю:
Решение
Теперь нам предстоит найти дополнительные множители. Разделим, согласно алгоритму, найденный общий знаменатель на знаменатели исходных дробей:
Так, мы привели исходные дроби к общему знаменателю. В случае необходимости далее можно преобразовать полученный результат в вид алгебраических дробей, осуществив умножение многочленов и одночленов в числителях и знаменателях.
Уточним также такой момент: найденный общий знаменатель оптимально оставлять в виде произведения на случай необходимости сократить конечную дробь.
Мы рассмотрели подробно схему приведения исходных алгебраических дробей к общему знаменателю, теперь можем приступить к разбору примеров на сложение и вычитание дробей с разными знаменателями.
Решение
Теперь сложим дроби, которые мы привели к общему знаменателю:
Полученную дробь возможно сократить на общий множитель x + 1 :
2 + 2 · x x · ( x + 1 ) · ( x + 2 ) = 2 · ( x + 1 ) x · ( x + 1 ) · ( x + 2 ) = 2 x · ( x + 2 )
И, напоследок, полученный результат запишем в виде алгебраической дроби, заменив произведение в знаменателе многочленом:
2 x · ( x + 2 ) = 2 x 2 + 2 · x
Запишем ход решения кратко в виде цепочки равенств:
Обратите внимание еще на такую деталь: перед тем, как алгебраические дроби сложить или вычесть, при наличии возможности их желательно преобразовать с целью упрощения.
Решение
Преобразуем исходные алгебраические дроби для упрощения дальнейшего решения. Вынесем за скобки числовые коэффициенты переменных в знаменателе:
Данное преобразование однозначно дало нам пользу: мы явно видим наличие общего множителя.
Совершим действие, которое нам позволит избавиться от дробных коэффициентов: умножим полученные дроби на 14 :
Наконец, выполним требуемое в условии задачи действие – вычитание:
Сложение и вычитание алгебраической дроби и многочлена
Решение
Теперь можем выполнить сложение по правилу сложения дробей с разными знаменателями:
Сложение и вычитание дробей
Рассмотрим непростую, но очень важную тему 5 класса по математике «сложение и вычитание дробей». Мы научимся складывать дроби как с общим, так и с разными знаменателями, разберёмся со смешанными дробями, научимся выполнять арифметические действия и с десятичными дробями.
Сложение и вычитание дробей с общим знаменателем
Допустим, по условию задания нам нужно найти сумму:
Так как в этом примере знаменатель у чисел одинаковый, это число 5, мы можем записать их под общую черту
Выполняем сложение числителей 2 и 1, 2 + 1 = 3
Тем самым получили
Знаменатель у дробей общий, записываем их под одну черту и выполняем вычитание числителей 11 – 3 = 8
Тем самым вы выполнили вычитание двух дробей с общим знаменателем.
Задание для самопроверки:
Сложение и вычитание дробей с разными знаменателями
Для выполнения сложения или вычитания дробей с разными знаменателями, необходимо в первую очередь найти наименьшее общее кратное (НОК) имеющихся знаменателей. НОК и есть общий знаменатель для дробей. Для этого вспомним, данную тему:
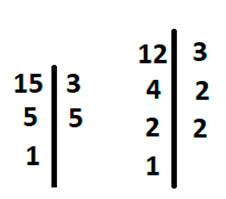
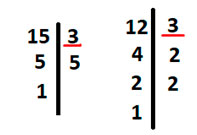
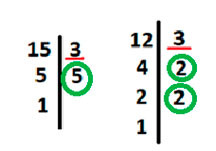
Найдем НОК (15,12). Для этого разложим каждое число на простые множители так, чтобы в конце получилась 1.
Подчеркнём одинаковые цифры во вторых столбцах у каждого числа.
Теперь возьмем первое число, то есть 15, и умножим его на неподчеркнутые цифры у второго числа. То есть 15 * 2 * 2, получим 60.
В первую очередь, найдем НОК знаменателей, 12 и 15.
Мы уже нашли его в предыдущем действии, НОК(12, 15) = 60
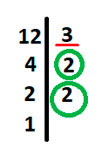
Теперь смотрим, на что нужно домножить первую дробь, чтобы ее знаменатель из 12 превратился в 60. Для этого вернемся к нахождению НОК и найдем неподчёркнутые цифры из другого столбца( смотрим на разложение числа 15), это число всего одно, 5. Мы поняли, что дополнительный множитель у первой дроби – это число 5.
Аналогично найдём дополнительный множитель для второй дроби, у второго числа 12 2 и 2 не подчёркнуты. 2*2 = 4 Следовательно дополнительный множитель для неё — это число 4.
Получившиеся доп. множители записываем соответственно в правом верхнем углу у каждой дроби. А затем умножаем числитель дробей на этот множитель, записываем получившееся выражение уже сверху дробной функции со знаменателем 60.
Выполним необходимые действия.
В итоге мы получили дробь, которая равна сумме двух первоначальных.
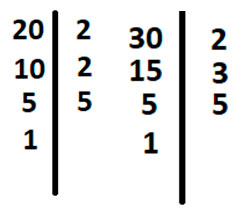
Также первоначально найдем НОК, разложим знаменатели дробей 20 и 30 на простые множители.
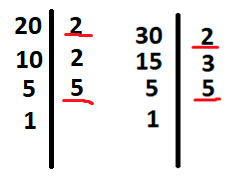
Подчеркнём одинаковые цифры в двух столбцах
Домножим 20 на неподчёркнутые цифры у 30, это лишь 3.
Значит общий знаменатель искомых дробей – 60.
Посмотрим, какой недостающий множитель у числа 20, это цифра 3 из второго столбца.
А доп. множитель у 30 – цифра 2 из первого столбика.
Записываем дроби под общий знаменатель, при этом не забываем умножать числители на соответственный доп. множитель.
Это окончательный ответ.
Задание для самопроверки:
Сложение и вычитание десятичных дробей
Для того, чтобы научиться складывать и вычитать десятичные дроби, мы должны в первую очередь правильно их записать, запятая у второго числа должна находиться строго под запятой у первого.
Cложение десятичных дробей
Для этого суммируем цифры, находящиеся друг под другом, начиная с крайней левой. Записываем получившиеся значения под вертикальную черту. Если под одной из цифр нижняя отсутствует, как у числа 2, просто списываем эту двойку вниз.
Пишем ответ, оставляя запятую на прежней позиции.
Вычитание десятичных дробей
Это делается абсолютно аналогично сложению. Запишем числа друг под другом, запятая под запятой.