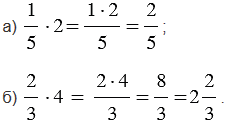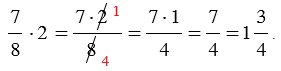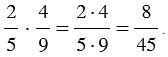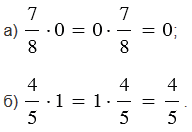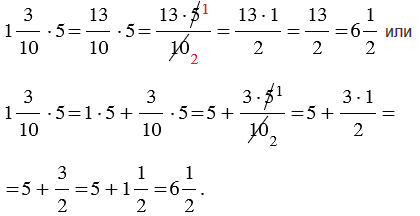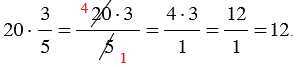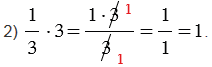Как выполнить умножение смешанных чисел
Умножение обыкновенных дробей
| Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения. |
Обратите внимание, если в ответе получается неправильная дробь, то из нее выделяют целую часть.
Если мы умножаем на натуральное число, которое можно сократить с числом, стоящим в знаменателе, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
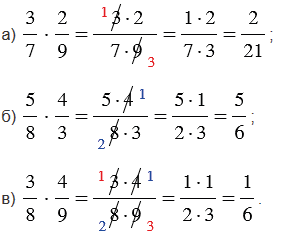
Если мы перемножаем дроби, у которых можно сократить числитель первой и знаменатель второй дроби и (или) знаменатель первой и числитель второй дроби, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).
Умножение смешанных чисел
| Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей. |
Для обыкновенных дробей, как и для натуральных чисел, выполняются свойства умножения (переместительное свойство умножения, сочетательное свойство умножения, распределительные свойства умножения относительно сложения и относительно вычитания). Также при умножении дроби на ноль (или нуля на дробь) получаем ноль, и при умножении дроби на единицу (или единицы на дробь) получим равную ей дробь.
| Чтобы умножить смешанное число на натуральное число, можно представить смешанное число в виде неправильной дроби, а затем воспользоваться правилом умножения дроби на натуральное число или можно умножить целую часть на натуральное число, далее умножить дробную часть на натуральное число и полученные произведения сложить. |
Нахождение дроби от числа
Примеры:
а) Найти 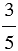
Решение:
б) Найти 0,6 от числа 9.
Решение:
в) Найти 30 % от числа 500.
Решение:
1) 30% = 30 : 100 = 0,30 = 0,3
Взаимно обратные числа
| Два числа, произведение которых равно 1, называют взаимно обратными. |
Примеры:
1) 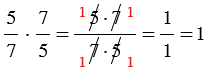
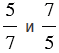
2)
Чтобы определить число обратное смешанному числу, нужно представить это смешанное число в виде неправильной дроби.
Пример:
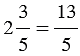
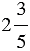
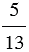
Запомните:
Поделись с друзьями в социальных сетях:
Умножение и деление смешанных чисел
Чтобы умножить или разделить смешанные числа, нужно представить их в виде неправильных дробей и выполнить требуемое действие с обыкновенными дробями.
Когда выполняется умножение смешанного числа на натуральное число (или наоборот), смешанное число можно не записывать в виде неправильной дроби. Такие примеры можно решить используя распределительный закон умножения:
Так как умножение сводится лишь к умножению целой части и числителя дробной части на натуральное число, то умножение смешанного и натурального числа обычно записывают без промежуточных вычислений в более краткой форме:
При делении смешанного числа на натуральное число (или наоборот), их можно представить в виде неправильных дробей и выполнить требуемое действие с обыкновенными дробями:
При умножении и делении смешанного числа на дробь (или наоборот), смешанное число переводится в неправильную дробь, после чего требуемое действие выполняется с обыкновенными дробями:
Калькулятор умножения и деления смешанных чисел
Математика. 5 класс
Конспект урока
Умножение смешанных дробей
Перечень рассматриваемых вопросов:
– умножение смешанной дроби на натуральное число;
– возведение смешанной дроби в степень;
– умножение смешанных дробей.
Распределительный закон умножения – чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Переместительный закон умножения – от перестановки множителей произведение не меняется.
Площадь прямоугольника – произведение длины на ширину.
Порядок убывания – расположение элементов от большего к меньшему.
Порядок возрастания – расположение элементов от меньшего к большему.
Теоретический материал для самостоятельного изучения
На предыдущих уроках вы научились умножать обыкновенные дроби и записывать смешанные дроби в виде неправильных.
Произведение двух дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.
Чтобы записать смешанную дробь неправильной дробью, надо знаменатель дробной части умножить на целую часть, прибавить числитель дробной части и полученное число записать в числитель, а знаменатель оставить прежним.
Этих умений достаточно, чтобы сегодня научиться умножать смешанные дроби.
Правило умножения смешанных дробей звучит так: чтобы умножить смешанные дроби, нужно записать их в виде неправильных дробей и выполнить умножение с обыкновенными дробями.
Результат получился тот же, что и при умножении.
Рассмотрим ещё один случай применения распределительного закона умножения для упрощения вычислений.
Найдём сумму произведения трёх целых четырёх пятых и пяти восьмых с произведением четырёх целых одной пятой и пяти восьмых.
В этих произведениях есть одинаковый множитель – пять восьмых. Его по распределительному закону вынесем за скобки, в которых останется сумма трёх целых четырёх пятых и четырёх целых одной пятой. Найдём значение суммы в скобках. Складываем отдельно целые части – три и четыре – это будет семь, и дробные части – четыре пятых и одну пятую – это будет пять пятых.
Сумму целой и дробной части записываем смешанной дробью – семь целых пять пятых и умножаем на пять восьмых. Так как дробная часть получившейся смешанной дроби – неправильная дробь, равная одному, то смешанную дробь заменяем на восемь целых. Умножаем восемь на пять восьмых – это пять.
Расставим порядок действий. Сначала выполняются действия в скобках. В скобках есть умножение и сложение. Умножение выполняется в первую очередь, затем сложение. Четвёртым действием будет вычитание из числа суммы в скобках. Пятое действие – нахождение частного в знаменателе. Шестое действие – деление числителя исходной дроби на знаменатель. Деление заменяется умножением, а умножать мы научились:
Итак, чтобы умножить смешанные дроби необходимо:
• представить эти смешанные дроби неправильными дробями;
• выполнить умножение неправильных дробей;
• сократить, если возможно;
• представить неправильную дробь, полученную в результате умножения, смешанной дробью.
При возведении смешанной дроби в степень нужно:
• представить эту смешанную дробь неправильной дробью;
• возвести полученную неправильную дробь в нужную степень.
№ 1. Поставьте на места пропусков числа так, чтобы вычисления были верными.
Как умножать смешанные числа
wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 15 человек(а).
Количество просмотров этой статьи: 25 261.
Смешанное число – число, состоящее из целой и дробной частей, например 3 ½. Перед умножением двух смешанных чисел их необходимо преобразовать в неправильные дроби. Эта статья расскажет вам, как умножить смешанные числа, следуя нескольким простым правилам.
При преобразовании числа 4 1 /2 в неправильную дробь сначала умножьте целую часть (4) на знаменатель дроби (2): 4*2 = 8.
Сложите полученное 8 и числитель 1: 8 + 1 = 9.
При преобразовании числа 6 2 /5 в неправильную дробь сначала умножьте целую часть (6) на знаменатель дроби (5): 6*5 = 30.
Сложите полученное 30 и числитель 2: 30 + 2 = 32.
Умножение смешанных чисел: правила, примеры, решения
Данная статья дана для разбора смешанных чисел. Научимся выполнять умножения смешанных чисел и натурального числа.
Умножение смешанных чисел
Умножение смешанных чисел сводится к умножению обыкновенных дробей. Для этого нужно сделать перевод смешанных чисел в неправильные дроби.
Используем правила умножения смешанных чисел:
Рассмотрим решения на примерах.
Чтобы закрепить знания умножения смешанных чисел, рассмотрим пример решения.
Мы раскладываем на простые множители и выполняем сокращение одинаковых множителей:
36 · 10 5 · 9 = 2 · 2 · 3 · 3 · 2 · 5 5 · 3 · 3 = 2 · 2 · 2 1 = 8
Ответ: 7 1 5 · 1 1 9 = 8 .
Умножение смешенного и натурального числа
После того, как произведется замена неправильной дробью, умножение смешенного и натурального числа сводится к умножению обыкновенной дроби и натурального числа.
41 · 45 18 = 41 · 3 · 3 · 5 2 · 3 · 3 = 41 · 5 2 = 205 2 = 102 1 2
Необходимо заменить смешанное число суммой целой или дробной его части. Далее используем свойство распределительного умножения:
10 3 8 · 8 = 10 + 3 8 · 8 = 10 · 8 + 3 8 · 8 = 80 + 3 = 83
Ответ: 10 3 8 · 8 = 83 .
Умножение смешанного числа и обыкновенной дроби
Умножение смешанного числа и обыкновенной дроби лучше представить в виде произведения обыкновенных дробей, умноженное на смешенное число неправильной дробью.