Как выполнять деление комплексных чисел
Деление комплексных чисел
Число, состоящее из вещественной и мнимой частей вида z = а + bi, является комплексным числом. Такие операции, как сложение и вычитание, умножение и деление двух комплексных чисел выполняются так же, как и соответствующие операции над действительными числами.
Деление выполняется для чисел, представленных в любой форме записи.
Деление комплексных чисел представляет собой операцию, обратную умножению. Вначале операцию деления надо записать в виде дроби, затем числитель и знаменатель умножить на выражение, сопряженное знаменателю.
Пусть даны два комплексных числа z1 = а + bi и z2 = с + di.
Деление этих чисел в алгебраической форме можно выразить формулой: 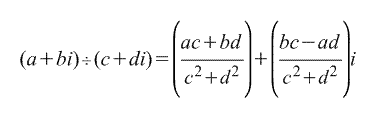
Деление в тригонометрической форме.
Пусть заданы 2 комплексных числа: 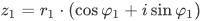
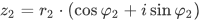
Модуль числа z обычно обозначается |z| или r. В нашем случае r1 — модуль числа z1, r2 — модуль z2.
Частное от деления рассчитаем по формуле: 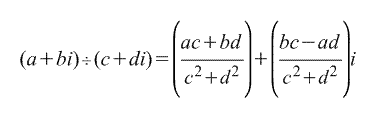
Т.е. чтобы найти частное от деления комплексных чисел, следует разделить их модули (r1 / r2) и определить разность аргументов делимого и делителя.
Правила деления комплексных чисел
Деление комплексных чисел — основные правила
Частным двух комплексных чисел \(z_<1>=a_<1>+b_ <1>i\) и \(z_<2>=a_<2>+b_ <2>\) i называют число z, заданное соотношением: \(z=\frac
Общий алгоритм для деления комплексных чисел на практике:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В каких формах это можно делать
Комплексные числа делят разными методами, подтвержденными доказательствами. Существуют алгебраическая, тригонометрическая и показательная формы для подобных операций. В каждом перечисленном случае необходимо использовать определенную формулу.
Формула деления в алгебраической форме
Когда требуется выполнить деление комплексных чисел в алгебраической форме, в первую очередь числитель и знаменатель умножают на число, сопряженное к знаменателю. Таким образом, удается исключить комплексность в знаменателе:
Формула деления в тригонометрической форме
Деление в тригонометрической форме подразумевает деление модулей комплексных чисел. После выполнения данной операции определяют разность аргументов:
Формула деления в показательной форме
Показательная форма деления комплексных чисел в тригонометрии предполагает деление модулей и вычисление разности аргументов в экспоненте:
Примеры решения задач
Необходимо найти частное пары комплексных чисел:
\(z_1 = 3+i\) и \(z_2 = 2-3i\)
Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.
Сопряженное комплексное число к знаменателю:
Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:
Далее следует привести подобные слагаемые и записать вывод с ответом:
Требуется выполнить деление комплексных чисел:
Комплексные числа в условии задачи записаны в тригонометрической форме. По этой причине необходимо использовать в расчетах соответствующую формулу. В данном случае следует определить деление модулей и разность аргументов:
Следующим шагом является деление чисел:
Нужно найти частное комплексных чисел:
Решение: Согласно формуле деления в показательной форме определяем разность аргументов и частное модулей:
При подстановке в формулу полученных значений уравнение будет преобразовано следующим образом:
В первую очередь следует домножить числитель и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю:
Данным числом является:
Затем следует перемножить комплексные числа, как алгебраические двучлены, с учетом:
Необходимо найти частное:
\(=2 \cdot\left[\cos \frac<\pi><2>+i \sin \frac<\pi><2>\right]=2 \cdot(0+i)=2 i\)
Необходимо разделить два комплексных числа:
С помощью соответствующей формулы можно записать уравнение:
Ответ: \( z_ <1>\div z_ <2>= 1+i\)
Необходимо вычислить частное комплексных чисел:
\(z_<1>=\sqrt <2>\left( \cos \frac<\pi> <2>+ i \sin \frac<\pi> <2>\right)\)
\(z_<2>=\sqrt <2>\left( \cos \frac<\pi> <4>+ i \sin \frac<\pi> <4>\right)\)
Используя соответствующую формулу, запишем:
\(z_ <1>\div z_ <2>= \frac
\(= 1 \cdot \left( \cos \frac<\pi> <4>+ i \sin \frac<\pi> <4>\right) = \cos \frac<\pi> <4>+ i \sin \frac<\pi><4>\)
Ответ: \( z_ <1>\div z_ <2>= \cos \frac<\pi> <4>+ i \sin \frac<\pi><4>\)
Требуется разделить два комплексных числа:
Используя соответствующую формулу деления комплексных чисел, можно решить уравнение:
Деление комплексных чисел
Вы будете перенаправлены на Автор24
Деление на число и деление заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.
Для деления заданных комплексных чисел на действительное число воспользуемся определением и получим:
Готовые работы на аналогичную тему
\[z_ <1>\cdot z_ <2>=\frac
Выполнить деление заданных комплексных чисел:
Для деления заданных комплексных чисел воспользуемся определением и получим:
Равенство, указанное в определении 3, достаточно сложно для запоминания, поэтому на практике при делении заданных комплексных чисел, представленных в алгебраической форме, используют алгоритм, который описан в примечании 5.
Чтобы выполнить операцию деления заданных комплексных чисел, представленных в алгебраической форме необходимо:
Выполнить деление комплексных чисел:
Для деления комплексных чисел воспользуемся алгоритмом, приведенным в примечании 5, и получим:
Выполнить деление комплексных чисел:
Для деления комплексных чисел воспользуемся определением и получим:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 11 2021
Комплексные числа
Формы
Так сложилось в математике, что у данных чисел несколько форм. Число одно и тоже, но записать его можно по-разному:
Далее с примерами решений вы узнаете как переводить комплексные числа из одной формы в другую путем несложных действий в обе стороны.
Изображение
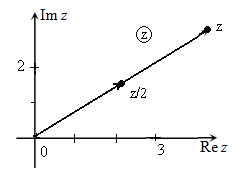
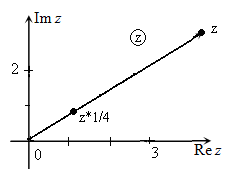
Изучение выше мы начали с алгебраической формы. Так как она является основополагающей. Чтобы было понятно в этой же форме изобразим комплексное число на плоскости:
Вычислить сумму и разность заданных комплексных чисел:
Сначала выполним сложение. Для этого просуммируем соответствующие мнимые и вещественные части комплексных чисел:
Аналогично выполним вычитание чисел:
Выполнить умножение и деление комплексных чисел:
Так, теперь разделим первое число на второе:
Суть деления в том, чтобы избавиться от комплексного числа в знаменателе. Для этого нужно домножить числитель и знаменатель дроби на комплексно-сопряженное число к знаменателю и затем раскрываем все скобки:
Разделим числитель на 29, чтобы записать дробь в виде алгебраической формы:
Для возведения в квадрат достаточно умножить число само на себя:
Пользуемся формулой для умножения, раскрываем скобки и приводим подобные:
В этом случае не всё так просто как в предыдущем случае, когда было возведение в квадрат. Конечно, можно прибегнуть к способу озвученному ранее и умножить число само на себя 7 раз, но это будет очень долгое и длинное решение. Гораздо проще будет воспользоваться формулой Муавра. Но она работает с числами в тригонометрической форме, а число задано в алгебраической. Значит, прежде переведем из одной формы в другую.
Вычисляем значение модуля:
Найдем чем равен аргумент:
$$ \varphi = arctg \frac<3> <3>= arctg(1) = \frac<\pi> <4>$$
Записываем в тригонометрическом виде:
Преобразуем в алгебраическую форму для наглядности:
Представим число в тригонометрической форме. Найдем модуль и аргумент:
Используем знакомую формулу Муавра для вычисления корней любой степени:
Алгебраические операции с комплексными числами
Содержание:
Действия над комплексными числами, заданными в алгебраической форме
Алгебраическая форма комплексного числа
Как отмечалось ранее, комплексное число можно задавать в виде 

Комплексное число, заданное в виде 
Рассмотрим действия над комплексными числами, заданными в алгебраической форме.
Сложение комплексных чисел
Следовательно, чтобы сложить два комплексных числа, нужно сложить их действительные части, что дает действительную часть суммы, и сложить мнимые части, что дает мнимую часть суммы.
Сумма комплексно-сопряжённых чисел всегда является действительным числом.

Свойства суммы комплексных чисел
1. Сложение комплексных чисел является коммутативным, то есть для любых комплексных чисел 
2. Сложение комплексных чисел является ассоциативным, то есть для любых комплексных чисел 
Возможно вам будут полезны данные страницы:
Вычитание комплексных чисел
Определение. Разностью двух комплексных чисел называется такое число, которое в сумме с вычитаемым дает уменьшаемое.
Вычитание комплексных чисел является всегда возможным.
Теорема Для любых комплексных чисел 

Докажем, что существует такое число 



Эта система уравнений имеет решение, и к тому же лишь одно, а именно:
что и нужно было доказать.
Разность комплексно-сопряжённых чисел всегда является мнимым числом.
Умножение комплексных чисел
Определение. Произведением двух комплексных чисел 

Произведение комплексно-сопряжённых чисел всегда является действительным числом.
Свойства произведения комплексных чисел
1. Умножение комплексных чисел является коммутативным, то есть для любых комплексных чисел 
2. Умножение комплексных чисел является ассоциативным, то есть для любых комплексных чисел 
3. Умножение комплексных чисел является дистрибутивным относительно сложения, то есть для любых комплексных чисел 
Деление комплексных чисел
Определение. Частным от деления комплексных чисел называется такое комплексное число, которое в произведении с делителем дает делимое, если делитель отличается от нуля.
Докажем, что всегда существует частное от деления двух комплексных чисел, если знаменатель отличается от нуля.
Теорема Частное 

Пусть 

Исходя из равенства комплексных чисел, имеем систему уравнений
Решив эту систему уравнений, находим
Следовательно, система уравнений имеет решение, и к тому же единственное. Тогда
ЗАМЕЧАНИЕ. Деление комплексных чисел в алгебраической форме удобно выполнять следующим образом. Числитель и знаменатель следует умножить на число, комплексно-сопряженное знаменателю, после чего в числителе и знаменателе выполнить умножение комплексных чисел по правилу умножения многочленов. Полученный результат записать в алгебраической форме.
Примеры с решением
Пример задачи с решением 2.1
Решение:
Использовав формулы (2.1), (2.2), (2.5), (2.6), получим:
Ответ:
Пример задачи с решением 2.2
Найти значение выражения
Решение:
Воспользовавшись правилом умножения многочленов, имеем
Ответ:
Пример задачи с решением 2.3
Решение:
Воспользуемся правилом умножения многочленов:
4) По формуле (2.8) имеем:
Ответ:
Пример задачи с решением 2.4
Решение:
Деление комплексных чисел можно выполнять по формуле (2.13), но проще это сделать, умножив числитель и знаменатель на число, комплексносопряжённое знаменателю.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).
Услуги:
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.