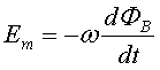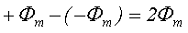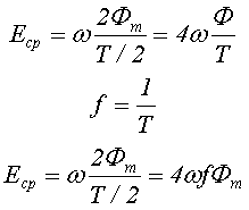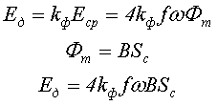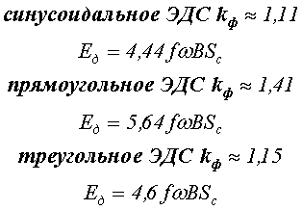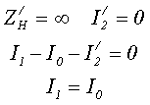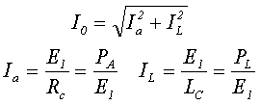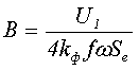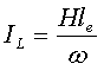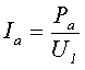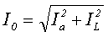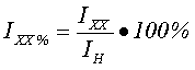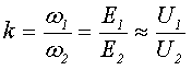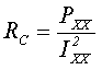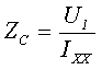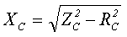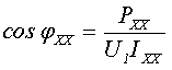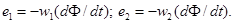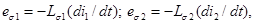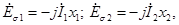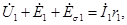Как выражается эдс рассеяния обмоток

Трансформаторы

1. Конструкция трансформатора

2. Работа трансформатора в режиме холостого хода

Под холостым ходом трансформатора понимается режим его работы при разомкнутой вторичной обмотке.
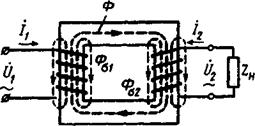
Первичная обмотка трансформатора подключена к источнику переменного напряжения. Ток i_1х первичной обмотки создает переменное магнитное поле, намагничивающее сердечник трансформатора.
Магнитный поток в трансформаторе разделим на две части: основной магнитный поток Ф, замыкающийся в сердечнике, и поток рассеяния Ф_1S, замыкающийся частично по воздуху.
На рис. 3 изображен трансформатор, работающий в режиме холостого хода.

Определим ЭДС, индуктированную в первичной обмотке трансформатора основным магнитным потоком.

.

Основной магнитный поток изменяется по синусоидальному закону

,

Мгновенное значение ЭДС

.

.

Действующее значение ЭДС в первичной обмотке

.

Для вторичной обмотки можно получить аналогичную формулу

.

Электродвижущие силы E₁ и E₂, индуктированные в обмотках трансформатора основным магнитным потоком, называются трансформаторными ЭДС. Трансформаторные ЭДС отстают по фазе от основного магнитного потока на 90°.
Магнитный поток рассеяния индуктирует в первичной обмотке ЭДС рассеяния

,

,

. (1)

Напряжение на первичной катушке имеет три слагаемых: падение напряжения, напряжение, уравновешивающее трансформаторную ЭДС, напряжение, уравновешивающее ЭДС рассеяния.
Запишем уравнение (1) в комплексной форме

. (2)

где индуктивное сопротивление рассеяния первичной обмотки.

На рис. 4 изображена векторная диаграмма трансформатора, работающего в режиме холостого хода.

На рис. 5 изображена схема замещения трансформатора, соответствующая уравнению (2).

Коэффициент трансформации экспериментально определяется из опыта холостого хода.

3. Работа трансформатора под нагрузкой

Если к первичной обмотке трансформатора подключить напряжение U₁, а вторичную обмотку соединить с нагрузкой, в обмотках появятся токи I₁ и I₂. Эти токи создадут магнитные потоки Ф₁ и Ф₂, направленные навстречу друг другу. Суммарный магнитный поток в магнитопроводе уменьшается. Вследствие этого индуктированные суммарным потоком ЭДС E₁ и E₂ уменьшаются. Действующее значение напряжения U₁ остается неизменным. Уменьшение E₁, согласно (2), вызывает увеличение тока токи I₁. При увеличении тока I₁ поток Ф₁ увеличивается ровно настолько, чтобы скомпенсировать размагничивающее действие потока Ф₂. Вновь восстанавливается равновесие при практически прежнем значении суммарного потока.
В нагруженном трансформаторе, кроме основного магнитного потока, имеются потоки рассеяния Ф_1S и Ф_2S, замыкающиеся частично по воздуху. Эти потоки индуктируют в первичной и вторичной обмотках ЭДС рассеяния.

, ,

. (3)

Для вторичной обмотки

, (4)

.

Трансформаторная ЭДС E₁, пропорциональная основному магнитному потоку, приблизительно равна напряжению на первичной катушке U₁. Действующее значение напряжения постоянно. Поэтому основной магнитный поток трансформатора остается неизменным при изменении сопротивления нагрузки от нуля до бесконечности.
Если , то и сумма магнитодвижущих сил трансформатора

. (5)

Уравнение (5) называется уравнением равновесия магнитодвижущих сил.
Уравнения (3), (4), (5) называются основными уравнениями трансформатора.
Из уравнения (5) получим формулу

. (6)

Согласно формуле (6), ток в первичной обмотке складывается из тока холостого хода, или намагничивающего тока, и тока, компенсирующего размагничивающее действие вторичной обмотки.
Умножим левую и правую части уравнения (4) на коэффициент трансформации K_T

. (7)

где приведенное активное сопротивление вторичной обмотки;

приведенное индуктивное сопротивление вторичной обмотки;

приведенное напряжение на нагрузке;

приведенное сопротивление нагрузки.
Величиной намагничивающего тока можно пренебречь, так как она мала по сравнению с током первичной обмотки трансформатора в нагрузочном режиме , тогда .
Подставим уравнение (7) в уравнение (3).
Получим

. (8)

Уравнению (8) соответствует упрощенная схема замещения трансформатора, изображенная на рис. 6.

Рис. 6

активное сопротивление короткого замыкания трансформатора,

индуктивное сопротивление короткого замыкания.

Параметры упрощенной схемы замещения определяются из опыта короткого замыкания. Для этого собирается схема рис. 7.

Рис. 7

Зажимы вторичной обмотки замыкаются накоротко. Измеряют напряжение, ток и мощность: U_1k, I_1k, P_k. Опыт короткого замыкания осуществляется при пониженном напряжении на первичной обмотке.
Затем вычисляют

.

На рис. 8 изображена векторная диаграмма трансформатора, соответствующая упрощенной схеме замещения. Нагрузкой трансформатора является активное сопротивление R_H.
Вектор тока совмещен с вещественной осью комплексной плоскости.

Рис. 8
Вектор напряжения на сопротивлении нагрузки совпадает с вектором тока по направлению. Вектор напряжения на индуктивном сопротивлении перпендикулярен, а вектор напряжения параллелен вектору тока. Вектор напряжения на входе трансформатора равен сумме трех векторов напряжения.
Упрощенная схема используется для расчета цепей, содержащих трансформаторы.

4. Специальные типы трансформаторов

Наиболее часто в электротехнических установках используются следующие специальные типы трансформаторов: автотрансформаторы, многообмоточные и трехфазные трансформаторы.

Автотрансформатором называется такой трансформатор, у которого имеется только одна обмотка, часть которой принадлежит одновременно вторичной и первичной цепям. Схема однофазного трансформатора изображена на рис. 9.

Режим холостого хода автотрансформатора, когда I₂ = 0, ничем не отличается от режима холостого хода обычного трансформатора.
Подводимое к трансформатору напряжение U₁ = U_AB равномерно распределяется между витками первичной обмотки.

где коэффициент трансформации.

Автотрансформаторы выгодно использовать в тех случаях, когда коэффициент трансформации близок к единице.
Многообмоточные (одна первичная и несколько вторичных) трансформаторы используются в радиотехнических схемах для получения нескольких напряжений.
В режиме холостого хода работа таких трансформаторов не отличается от двухобмоточных.
В трехфазной сети переменного тока преобразование напряжений осуществляется с помощью трехфазного трансформатора с общим для трех фаз сердечником. В трехфазном трансформаторе с общим магнитопроводом магнитный поток любой из фаз может замыкаться через стержни, на которых расположены обмотки двух других фаз. Затраты стали на трехфазный трансформатор значительно меньше, чем на три однофазных трансформатора.

Источник

ElectronicsBlog

Обучающие статьи по электронике

Режимы работы трансформатора. Часть 1

Всем доброго времени суток! В прошлой статье я рассказывал об устройстве трансформатора и его работе. Также я указывал, что для анализа трансформатора используют эквивалентные схемы, содержащие основные параметры трансформатора и позволяющие оценить его характеристики в различных режимах. В процессе своей работы трансформатор может находиться в трёх основных режимах: режим холостого хода, режим короткого замыкания и номинальный режим.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Для рассмотрения работы трансформатора в различных режимах мы будем использовать схему замещения трансформатора.

Рабочий процесс трансформатора

Процесс работы трансформатора рассмотрим на основе эквивалентной схемы замещения из предыдущей статьи

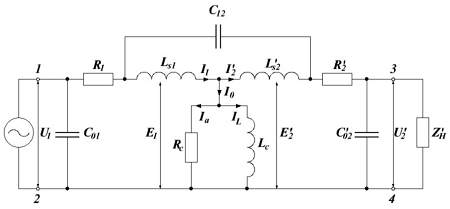
Эквивалентная схема замещения трансформатора.

При наличии нагрузки Z_H на выводах вторичной обмотки 3-4 и напряжении U₁ на выводах первичной обмотки 1-2 в магнитопроводе трансформатора создается магнитный поток, который индуцирует в обмотках ЭДС: в первичной – Е₁, а во вторичной – Е₂. В результате приложенное напряжение в первичной обмотке U₁ уравновешивается ЭДС Е₁ и падением напряжения на активном сопротивлении обмотки R₁ и реактивном сопротивлении L_s1 индуктивности рассеяния. Аналогичным образом происходит уравновешивание напряжения и во вторичной обмотке трансформатора.

Определение основных параметров трансформатора: напряжения U₁ и U₁, ЭДС Е₁ и Е₂, потери в обмотках и в магнитопроводе происходит при рассмотрении режимов работы трансформатора, а определение их реальных значений – из опытов холостого хода и короткого замыкания.

От чего зависит ЭДС в обмотках трансформатора?

В прошлой статье я указал, что мгновенное значение ЭДС в обмотке трансформатора определяется числом витков ω провода в ней и скоростью изменения магнитного потока dΦ/dt

где ω – число витков обмотки трансформатора,

dФ_В/dt – скорость изменения магнитного потока.

Однако в большинстве случаев нам интересно не мгновенное значение ЭДС, а действующее. Поэтому выведем выражение, определяющее действующее значение ЭДС в обмотках трансформатора. Это можно сделать аналитически проинтегрировав функцию изменения магнитного потока dΦ/dt, либо же путем нахождения среднего значения ЭДС E_cp и коэффициента формы ЭДС k_ф. Я буду выводить выражение вторым способом.

Магнитный поток протекая в сердечнике трансформатора изменяется в соответствии с некоторой периодичной функцией имеет два амплитудных значения максимальное +Ф_m и минимальное –Ф_m, тогда полное изменение магнитного потока за полупериод Т/2 будет иметь значение

Тогда среднее значение ЭДС Е_ср в обмотке трансформатора будет иметь вид

где ω – число витков обмотки трансформатора,

Т/2 – полупериод изменения функции магнитного потока,

f – частота изменения магнитного потока,

Действующее значение ЭДС и её среднее значение связывает коэффициент формы кривой ЭДС k_ф, тогда действующее значение ЭДС в обмотке трансформатора будет определяться следующим выражением

где k_ф – коэффициент формы ЭДС,

f – частота изменения ЭДС,

ω – число витков обмотки трансформатора,

B – магнитная индукция в сердечнике,

S_c – площадь сечения сердечника трансформатора.

Приведём примеры действующего значение ЭДС для синусоидального, прямоугольного (меандр) и треугольного изменения

Из вышесказанного следует, что при условии постоянства электромагнитной индукции B, ЭДС пропорциональна конструктивным параметрам трансформатора сечению магнитопровода S_c и количеству витков ω. Правильный выбор величины электромагнитной индукции В является одной из ключевых задач при проектировании трансформатора. Кроме того, с ростом частоты f увеличивается ЭДС, поэтому для реализации одинаковой ЭДС с ростом частоты требуются меньшие размеры и вес трансформатора. Данный фактор является основным преимуществом трансформаторов высокой частоты, которые чаще всего применяются в настоящее время.

Режим холостого хода

Данный режим характеризуется отсутствием нагрузки во вторичной обмотке или же бесконечно большой величиной сопротивления Z_H = ∞, то есть разомкнутая цепь вторичной обмотки.

Тогда ток во вторичной обмотке будет равен нулю I₂ = 0. Тогда в соответствии с первым законом Кирхгофа (закон баланса токов) получим

где I₁ – ток в первичной обмотке трансформатора,

I₀ – ток намагничивания магнитопровода,

I’₂ – приведённый ток вторичной обмотки трансформатора.

Возникновение тока намагничивания I₀ связанно с потерями энергии: на создание основного магнитного потока, замыкающегося через магнитопровод (мощность намагничивания P_L) и потери мощности в сердечнике Р_А, а так же вследствие потерь в первичной обмотке магнитопровода от протекания тока намагничивания. Так как трансформатор в режиме холостого хода не создает тока во вторичной обмотке I₂ = 0, то такой ток называют током холостого хода.

Очевидно, что ток холостого хода имеет активную I_a и реактивную I_L составляющие, которые определяются следующими выражениями

где Е₁ – ЭДС самоиндукции, возникающая в первичной обмотке,

R_C – сопротивление активных потерь в сердечнике,

L_C – сопротивление реактивных потерь в сердечнике.

Так как сопротивления R_C и L_C имеют нелинейных характер, то в инженерных расчётах пользуются графическими зависимостями параметров сердечников, в первую очередь кривой намагничивания материала магнитопровода (зависимость магнитной индукции В от напряженности магнитного поля Н Dynamic magnetization curves). Кроме того необходимо знать геометрические параметры используемого сердечника: эквивалентную площадь сечение S_e(A_e), эквивалентную длину магнитной силовой линии l­_e и эквивалентный объем сердечника V_e. Кроме того для нахождения потерь мощности в сердечнике Р_А необходимо воспользоваться графической зависимостью магнитных потерь в сердечнике (Relative core losses) от различных факторов: индукции B, температуры T и частоты f.

Как определить ток холостого хода трансформатора?

Вычисление тока холостого хода трансформатора может происходить следующим образом:

где k_ф – коэффициент формы ЭДС,

f – частота изменения ЭДС,

ω – число витков обмотки трансформатора,

S_c – площадь сечения сердечника трансформатора.

Полученное токам образом значение тока холостого хода практически не отличается от реальной величины тока, протекающего в первичной обмотке при работе трансформатора в режиме холостого хода.

Опыт холостого хода

После изготовления трансформатора необходимо провести ряд испытаний, одним из которых является опытом холостого хода. Данное испытание трансформатора проводится при разомкнутой вторичной обмотке и подачей номинального напряжения на первичную обмотку. По результатам проведения опыта холостого хода определяют коэффициент трансформации и мощность потерь в магнитопроводе.

Для проведения опыта холостого хода собирают схему изображенную ниже

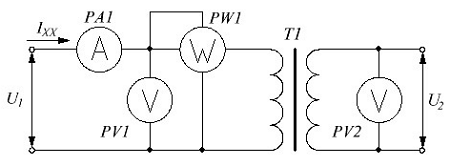
Схема опыта холостого хода.

Как видно на схеме к первичной обмотке трансформатора необходимо подключить вольтметр PV1, амперметр РА1 и ваттметр PW1, а к вторичной обмотке – вольтметр PV2.

Для снятия характеристик холостого хода трансформатора на его первичную обмотку подают номинальное напряжение = U_H, которое можно изменять при необходимости снятия динамических характеристик примерно от 30% до 110% U_H. После подачи напряжения в первичную обмотку снимают показания по приборам: ток холостого хода I_ХХ, мощность холостого хода Р_ХХ, напряжение на вторичной обмотке U₂ трансформатора.

По результатам проведения опыта холостого хода можно определить следующие параметры:

— процентное отношение тока холостого тока I_XX%

где I_H – номинальное значение тока в первичной обмотке трансформатора.

— коэффициент трансформации трансформатора k

где U₁ и U₂ – напряжения, снимаемые с вольтметров PV1 и PV2, соответственно.

— активное сопротивление намагничивающего контура R_C

где Р_ХХ – мощность, снимаемая с ваттметра PW1.

— полное сопротивление намагничивающего контура Z_C

— реактивное сопротивление намагничивающего контура Х_С

— коэффициент мощности холостого хода cos φ_XX

При проведении опыта холостого хода следует отметить, что в начальный момент подачи напряжения возникает недопустимо большой ток в разы превышающий номинальный, а так как ток холостого хода составляет 3 – 10 % от номинального тока, то пусковой ток превышает ток холостого тока в десятки раз. Поэтому в начальный момент необходимо замкнуть выводы амперметра РА1.

Кроме опыта холостого хода для испытания трансформатора проводят опыт короткого замыкания, о котором я расскажу в следующей статье.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник

Уравнения напряжений трансформатора

Основной переменный магнитный поток Ф в магнитопроводе трансформатора, сцепляясь с витками обмоток w₁ и w₂ (см. рис. 1.1), наводит в них ЭДС [см. (1.1) и (1.2)]

Предположим, что магнитный поток Ф является синусоидальной функцией времени, т. е.

, (1.4)

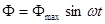
где Ф_max — максимальное значение потока.

Тогда, подставив (1.4) в формулу ЭДС е₁ и дифференцируя, получим

. (1.5)

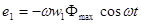
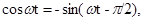
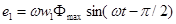
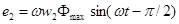
Но так как то

. (1.6)

, (1.7)

Из (1.6) и (1.7) следует, что ЭДС е\ и е₂ отстают по фазе от по­тока Ф на угол п/2. Максимальное значение ЭДС

(1.8)

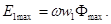
Разделив E_1maxна √2 и подставив ω = 2πf, получим действующее значение первичной ЭДС (В):

(1.9)

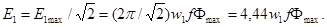
Аналогично, для вторичной ЭДС

(1.10)

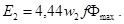
Отношение ЭДС обмотки высшего напряжения к ЭДС обмотки низшего напряжения называют коэффициентом трансформации:

(1.11)

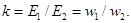
При практических расчетах коэффициент трансформации с некоторым допущением принимают равным отношению номинальных напряжений обмоток ВН и НН:

Рис. 1.14. Магнитные потоки в однофазном трансформаторе

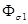
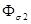
Токи I₁ и I₂ в обмотках трансформатора помимо основного магнитного потока Ф создают магнитные потоки рассеяния и (рис. 1.14), каждый из которых сцеплен с витками лишь собственной обмотки и индуцирует в ней ЭДС рассеяния. Эти ЭДС в первичной и вторичной обмотках таковы:

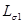
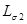
где и — индуктивности рассеяния.

Так как магнитные потоки рассеяния замыкаются главным образом в немагнитной среде (воздух, масло, медь), магнитная проницаемость которой постоянна, то и индуктивности L_s1 и L_s2 можно считать постоянными.

Действующие значения ЭДС рассеяния пропорциональны токам в соответствующих обмотках:

где x₁ и x₂ — индуктивные сопротивления рассеяния первичной и вторичной обмоток соответственно, Ом (знак минус в этих выражениях свидетельствует о реактивности ЭДС рассеяния).

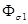
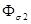
Таким образом, в каждой из обмоток трансформатора индуцируются по две ЭДС: ЭДС от основного потока Ф и ЭДС от потока рассеяния ( в первичной обмотке и во вторичной обмотке).

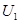
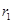
Для первичной цепи трансформатора, включенной в сеть на напряжение , с учетом падения напряжения в активном сопротивлении первичной обмотки можно записать уравнение напря­жений по второму закону Кирхгофа:

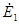
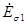
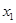
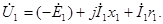
или, перенеся ЭДС и в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния , получим уравнение напряжений для первичной цепи трансформатора:

(1.13)

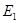
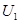
ЭДС первичной обмотки , наведенная основным магнитным потоком Ф, представляет собой ЭДС самоиндукции, а поэтому находится в противофазе с подведенным к первичной обмотке напряжением .

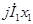
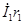
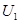
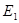
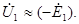
Обычно индуктивное и активное падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение уравновешивается ЭДС , т. е.

(1.14)

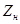
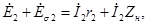
Для вторичной цепи трансформатора, замкнутой на нагрузку с сопротивлением , уравнение напряжений имеет вид

(1.15)

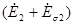
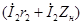
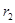
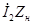
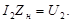
т.е. сумма ЭДС, наведенных во вторичной обмотке , уравновешивается суммой падений напряжений . Здесь — активное сопротивление вторичной обмотки. Падение напряжения на нагрузке представляет собой напряжение на выводах вторичной обмотки трансформатора:

(1.16)

Приведем уравнение (1.15) к виду, аналогичному уравнению ЭДС для первичной цепи (1.13). При этом учтем выражения (1.12) и (1.16) и получим уравнение напряжений для вторичной цепи трансформатора:

(1.17)

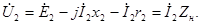
Из этого уравнения следует, что напряжение на выходе нагруженного трансформатора отличается от ЭДС вторичной обмотки на величину падения напряжений в этой обмотке.

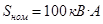
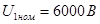
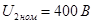
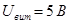
Пример1.2. Имеется однофазный трансформатор (рис. 1.14) номинальной мощностью и номинальными напряжениями и , при частоте тока f = 50 Гц; действующее значение напряжения, приходящееся на один виток обмоток, .

Определить: числа витков обмоток трансформатора w_l и w₂ поперечное сечение обмоточных проводов первичной q₁ и вторичной q₂ обмоток, если плотность тока в этих проводах D =• 4,0 А/мм 2 ; площадь поперечного сечения стержня магнитопровода Q_ст, если максимальное значение магнитной индукции в стержне B_ст, = 1,4Тл.

Решение. По номинальным значениям напряжений U_1ном, и U_2ном определяем числа витков в обмотках:

I_1HOM = S_ном /U₁ = 100• 10 3 /6000 = 16,7 А; I_2ном = S_ном / U₂ = 100• 10 3 /400 = 250 А. Поперечные сечения обмоточных проводов:

Основной магнитный поток в стержне определим, используя выражение (1.10) и учитывая, что номинальное вторичное напряжение U_2ном = Е₂:

Ф_max = Е₂ /(4,44fw₂) = 400/(4,44 • 50 • 80) = 0,0225 Вб. Поперечное сечение стержня магнитопровода

где k_с = 0,93 — коэффициент заполнения шихтованного стержня сталью, учитывающий увеличение сечения стержня прослойками изоляционного лака между стальными полосами.

Источник