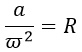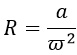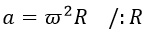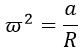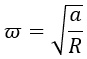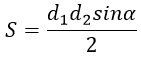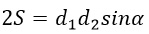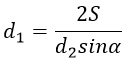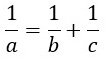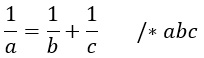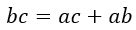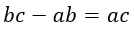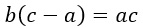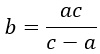Как выражать переменные в физике
Выведение переменной из формулы
Данную статью я начну с общего алгоритма выражения переменной, а затем уже будем разбираться на конкретных примерах.
Пусть дана какая-то формула.
1) Если она содержит скобки, то раскрываем их и приводим подобные слагаемые;
2) Если есть знаменатель, то избавляемся от него, умножив обе части формулы на этот знаменатель (если знаменателей несколько, то умножаем обе части равенства на общий знаменатель);
3) Если есть корни, то обе части возводим в степень, равную показателю корня;
4) Переносим все члены с нужной нам переменной в одну сторону;
5) Если таких членов несколько, то выносим нужную нам переменную за скобку в качестве общего множителя. Если нет, то этот шаг пропускаем.
6) Делим обе части формулы на все сомножители нужной нам переменной.
7) Если нужная переменная возведена в n-ую степень, то нужно из обеих частей формулы извлечь корень n-ой степени.
На самом деле, всё не так ужасно) На ОГЭ так вообще простые задания.
Вот парочка примеров.
Выразим радиус R, разделив обе части на его сомножитель ω 2 :
Но обычно пишут так, чтобы искомая переменная была слева:
Теперь выразим угловую скорость. Разделим обе части равенства на сомножитель угловой скорости (на R, короче говоря):
Получается вот такая запись:
Нужная нам угловая скорость возведена в квадрат. Избавиться от степени нам поможет квадратный корень:
Теперь возьмем формулу с дробью.
2) Площадь четырехугольника можно вычислить по формуле
Выразим из нее d1.
Избавляемся от знаменателя, умножив обе части равенства на 2 (т.к. знаменатель равен двум).
Чтобы выразить d1 разделим обе части на сомножители d2 и sinα.
Точно также выражаются d2 и sinα. Можешь даже самостоятельно попробовать.
Еще один пример. Последний.
3) Дана формула
Выразим из нее переменную b.
Формула содержит дроби, поэтому надо избавится от знаменателей. Умножим обе части равенства на общий знаменатель abc.
Получится такое выражение:
Перенесем все члены равенства, содержащие переменную b в левую часть.
Вынесем b за скобки как общий множитель.
Что-то не выражается? Напиши мне свой пример. Используй функцию «Предложить новость».
Как выражать переменные?
Как выражать переменные?
А то чего то забыл Ну например : u(скорость) = S / t.
Как например выразить отсюда S и t.
Примерно так пользуйся.
Как из физической формулы Q = сmt выразить переменную m?
Как из физической формулы Q = сmt выразить переменную m.
Нужно выразить отсюда массу(обе)?
Нужно выразить отсюда массу(обе).
Напишите чему отсюда равна m?
Напишите чему отсюда равна m.
Как отсюда вывести h?
Как отсюда вывести h?
Выразить из формулы все переменные V = V0( в нулевой степени) + а * t?
Выразить из формулы все переменные V = V0( в нулевой степени) + а * t.
В чем различие сжимаемости газов, жидкостей и твердых тел?
В чем различие сжимаемости газов, жидкостей и твердых тел?
Какие выводы отсюда следует?
1)Формула работы A = FS, отсюда S = A / F, S = 500 / 100 = 5 метров. 2)По формуле трения, выразить m.
Нагреть его посильнее.
Вариант 4 1) 2 2) газообразных 3)3 4)1 5)3 6)1 7) уменьшается Вариант 3 1) Увеличевается 2)1 3)2 4)1 5)3 6)1 7)1 Вариант 2 1)1 2) 2 3) 1 4) 3 5) 2 6) 1 7) 1 Вариант 1 1) 1 2) 2 3) 1 4) 2 5) 3 6)1 7) 3.
Масса : m = V * p плотность : p = m / v обьем : V = m / p.
Как работать с формулой, чтобы выразить из нее указанную переменную

Как работать с формулой, чтобы выразить из нее указанную переменную
1. а) Если формула содержит дроби, то сначала нужно избавиться от них, умножив обе части формулы на общий знаменатель;
б) если формула содержит корень, то нужно избавиться от него, возведя обе части формулы в квадрат;
в) если формула содержит дроби и корень, то нужно выполнить действия а) и б) в удобной последовательности.
2. Слагаемое (слагаемые), содержащие переменную, которую нужно выразить, перенести в левую часть, если они не находятся там. Иногда для этого достаточно просто поменять местами левую и правую части формулы.
3. Привести левую часть к виду, в котором нужная переменная будет являться одним из множителей. Иногда для этого нужно будет сгруппировать слагаемые, то есть выполнить разложение на множители левой части формулы.
4. Разделить обе части формулы на лишние множители, находящиеся в левой части, чтобы произошло сокращение, и нужная переменная осталась в левой части одна-единственная.
5. Если полученная таким образом переменная находится в степени, то нужно извлечь из обеих частей формулы корни этой же степени.
При разборе примеров, объясняйте себе каждый шаг!!

Как работать с формулой, чтобы выразить из нее указанную переменную
1. а) Если формула содержит дроби, то сначала нужно избавиться от них, умножив обе части формулы на общий знаменатель;
б) если формула содержит корень, то нужно избавиться от него, возведя обе части формулы в квадрат;
в) если формула содержит дроби и корень, то нужно выполнить действия а) и б) в удобной последовательности.
2. Слагаемое (слагаемые), содержащие переменную, которую нужно выразить, перенести в левую часть, если они не находятся там. Иногда для этого достаточно просто поменять местами левую и правую части формулы.
3. Привести левую часть к виду, в котором нужная переменная будет являться одним из множителей. Иногда для этого нужно будет сгруппировать слагаемые, то есть выполнить разложение на множители левой части формулы.
4. Разделить обе части формулы на лишние множители, находящиеся в левой части, чтобы произошло сокращение, и нужная переменная осталась в левой части одна-единственная.
5. Если полученная таким образом переменная находится в степени, то нужно извлечь из обеих частей формулы корни этой же степени.
При разборе примеров, объясняйте себе каждый шаг!!
Как научиться преобразовывать формулы по физике. Как выразить одну переменную через другую? Как выразить переменную из формулы? Союз с математикой
Физика – наука о природе. Она описывает процессы и явления окружающего мира на макроскопическом ярусе – ярусе маленьких тел, сравнимых с размерами самого человека. Для изложения процессов физика использует математический агрегат.
Инструкция
3. Выходит, выучите определения физических величин, относящихся к рассматриваемой теме. У всякой величины есть свой физический толк, тот, что вы обязаны понимать. Скажем, 1 кулон – это заряд, проходящий через поперечное сечение проводника за 1 секунду при силе тока в 1 ампер.
5. Путем математических реформирований дозволено из первичных формул вывести вторичные. Если вы обучитесь делать это легко и стремительно, последние дозволено будет не запоминать. Стержневой способ реформирований – способ подстановки: какая-нибудь величина выражается из одной формулы и подставляется в иную. Главно лишь, дабы эти формулы соответствовали одному и тому же процессу либо явлению.
6. Также уравнения дозволено складывать между собой, разделять, перемножать. Функции по времени дюже зачастую интегрируют либо дифференцируют, получая новые зависимости. Логарифмирование подойдет для степенных функций. При итоге формулы опирайтесь на итог, тот, что вы хотите в результате получить.
Каждая человеческая жизнь окружена большинством разновидных явлений. Ученые-физики занимаются постижением этих явлений; их инструментарием выступают математические формулы и достижения предшественников.
Природные явления
Изучение природы помогает умней относиться к имеющимся источникам, открывать новые источники энергии. Так, геотермальные источники обогревают примерно всю Гренландию. Само слово «физика» восходит к греческому корню «физис», что обозначает «природа». Таким образом, сама физика – наука о природе и природных явлениях.
Вперед, в грядущее!
Часто физики в прямом смысле «опережают время», открывая законы, которые находят использование лишь десятками лет (и даже столетиями) позднее. Никола Тесла открывал законы электромагнетизма, которые находят использование в наши дни. Пьер и Мария Кюри открыли радий фактически без поддержки, в невероятных для современного ученого условиях. Их открытия помогли спасти десятки тысяч жизней. Теперь физики каждого мира сосредоточены на вопросах Вселенной (макрокосмос) и мельчайших частиц вещества (нанотехнологии, микрокосмос).
Понимание мира
Важнейшим мотором общества является любознательность. Вот отчего эксперименты в Большом Андронном Коллайдере имеют такую высокую важность и спонсируются союзом из 60 государств. Имеется настоящая вероятность раскрыть тайны общества.Физика – наука фундаментальная. Это значит, что всякие открытия физики дозволено применять в иных сферах науки и техники. Небольшие открытия в одной ветви могут поразительно повлиять на всю «соседнюю» ветвь целиком. В физике знаменита практика изыскания группами ученых из различных стран, принята политика помощи и сотрудничества.Тайна мироздания, материи волновала великого физика Альберта Эйнштейна. Он предложил теорию относительности, поясняющую, что поля гравитации искривляют пространство и время. Апогеем теории стала известная формула E = m * C * C, объединяющая энергию с массой.
Союз с математикой
Физика опирается на новейшие математические инструменты. Нередко математики открывают абстрактные формулы, выводя новые уравнения из существующих, применяя больше высокие ярусы абстракции и законы логики, делая храбрые догадки. Физики следят за становлением математики, и изредка научные открытия абстрактной науки помогают пояснять незнакомые дотоле природные явления.Бывает и напротив – физические открытия толкают математиков на создание догадок и нового логичного агрегата. Связь физики и математики – одной из важнейших научных дисциплин подкрепляет авторитет физики.
Воспользовавшись записью первого начала термодинамики в дифференциальной форме (9.2), получим выражение для теплоёмкости произвольного процесса:
Представим полный дифференциал внутренней энергии через частные производные по параметрам и :
После чего формулу (9.6) перепишем в виде
Соотношение (9.7) имеет самостоятельное значение, поскольку определяет теплоёмкость в любом термодинамическом процессе и для любой макроскопической системы, если известны калорическое и термическое уравнения состояния.
Исходя из полученной формулы, можно легко найти связь между теплоемкостями и в идеальном газе. Этим мы и займемся. Впрочем, ответ уже известен, мы его активно использовали в 7.5.
Уравнение Роберта Майера
Выразим частные производные в правой части уравнения (9.8), с помощью термического и калорического уравнений, записанных для одного моля идеального газа. Внутренняя энергия идеального газа зависит только от температуры и не зависит от объёма газа, следовательно
Из термического уравнения легко получить
Подставим (9.9) и (9.10) в (9.8), тогда
Вы, надеюсь, узнали (9.11). Да, конечно, это уравнение Майера. Еще раз напомним, что уравнение Майера справедливо только для идеального газа.
9.3. Политропические процессы в идеальном газе
Как отмечалось выше первое начало термодинамики можно использовать для вывода уравнений процессов, происходящих в газе. Большое практическое применение находит класс процессов, называемых политропическими. Политропическим называется процесс, проходящий при постоянной теплоемкости .
Вывод уравнения политропического процесса в идеальном газе
Требование постоянства теплоёмкости в процессе позволяет записать первое начало термодинамики в виде
Используя уравнение Майера (9.11) и уравнение состояния идеального газа, получаем следующее выражение для
Разделив уравнение (9.12) на T и подставив в него (9.13) придем к выражению
Интегрированием (9.15), получаем
Это уравнение политропы в переменных
Параметр называется показателем политропы, который может принимать согласно () самые разные значения, положительные и отрицательные, целые и дробные. За формулой () скрывается множество процессов. Известные вам изобарный, изохорный и изотермический процессы являются частными случаями политропического.
К этому классу процессов относится также адиабатный или адиабатический процесс . Адиабатным называется процесс, проходящий без теплообмена (). Реализовать такой процесс можно двумя способами. Первый способ предполагает наличие у системы теплоизолирующей оболочки, способной изменять свой объем. Второй – заключается в осуществлении столь быстрого процесса, при котором система не успевает обмениваться количеством теплоты с окружающей средой. Процесс распространения звука в газе можно считать адиабатным благодаря его большой скорости.
где – показатель адиабаты.
В этом случае уравнение политропы принимает вид
Уравнение адиабатного процесса (9.20) называют также уравнением Пуассона, поэтому параметр часто именуют постоянной Пуассона. Постоянная является важной характеристикой газов. Из опыта следует, что ее значения для разных газов лежат в интервале 1,30 ÷ 1,67, поэтому на диаграмме процессов адиабата «падает» более круто, чем изотерма.
Графики политропических процессов для различных значений представлены на рис. 9.1.
На рис. 9.1 графики процессов пронумерованы в соответствии с табл. 9.1.
Этот урок – полезное дополнение к предыдущей теме » «.
Собственно, вся теоретическая часть подобных заданий представляет собой одну единственную фразу. Универсальную и простую до безобразия.
Удивляемся, но запоминаем:
Любое равенство с буквами, любая формула – это ТОЖЕ УРАВНЕНИЕ!
Ах, вы в курсе? Отлично! Тогда применяем теоретические знания на практике.
Как выразить одну переменную через другую?
Такая задача постоянно возникает при решении систем уравнений. Например, имеется равенство:
Здесь две переменные – икс и игрек.
Что означает это задание? Оно означает, что мы должны получить некоторое равенство, где слева стоит чистый икс. В гордом одиночестве, безо всяких соседей и коэффициентов. А справа – что уж получится.
И как же нам получить такое равенство? Очень просто! С помощью всё тех же старых добрых тождественных преобразований! Вот и применяем их в удобном нам порядке, шаг за шагом добираясь до чистого икса.
Анализируем левую часть уравнения:
Полдела сделано. Осталась тройка перед иксом. Как от неё избавиться? Разделить обе части на эту самую тройку! Т.е. задействовать второе тождественное преобразование.
Можно было бы сначала поделить обе части на тройку, а затем – переносить. Но это привело бы к появлению дробей в процессе преобразований, что не очень удобно. А так, дробь появилась лишь в самом конце.
Напоминаю, что порядок преобразований никакой роли не играет. Как нам удобно, так и делаем. Самое главное – не порядок применения тождественных преобразований, а их правильность!
А можно из этого же равенства
А почему – нет? Можно! Всё то же самое, только на этот раз нас интересует слева чистый игрек. Вот и очищаем игрек от всего лишнего.
Осталась двойка с минусом. Делим обе части на (-2):
И все дела.) Мы выразили y через х. Переходим к более серьёзным заданиям.
Как выразить переменную из формулы?
Например, такое задание:
выразить переменную с.
Однако… Как нам эту самую с вытаскивать-то?
Следующим шагом надо вытащить с из числителя дроби. Как? Легко! Избавимся от дроби. Нету дроби – нету и числителя.) Умножаем обе части формулы на 2:
Осталась элементарщина. Обеспечим справа букве с гордое одиночество. Для этого переменные a и b переносим влево:
Вот и всё, можно сказать. Осталось переписать равенство в привычном виде, слева направо и – ответ готов:
Это было несложное задание. А теперь задание на основе реального варианта ЕГЭ:
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость погружения батискафа вычисляется по формуле
где с = 1500 м/с – скорость звука в воде,
f 0 – частота испускаемых импульсов (в МГц),
f – частота отражённого от дна сигнала, регистрируемая приёмником (в МГц).
Определите частоту отражённого сигнала в МГц, если скорость погружения батискафа равна 2 м/с.
Напрямую, естественно, букву f никак не выдернешь, она снова в дробь запрятана. Причём и в числитель и в знаменатель. Поэтому самым логичным шагом будет избавиться от дроби. А там – видно будет. Для этого применяем второе преобразование – умножаем обе части на знаменатель.
А вот тут – очередные грабли. Прошу обратить внимание на скобки обеих частях! Частенько именно в этих самых скобочках и кроются ошибки в подобных заданиях. Точнее, не в самих скобочках, а в их отсутствии.)
А вот теперь скобки и раскрыть можно:
Осталось всего ничего. Делим обе части на скобку (v — c ) и – дело в шляпе!
Вот такое выражение. А вот теперь и числовые данные подставить можно. Получим:
Вот и всё. Надеюсь, общая идея понятна.
Или, скажем, логарифмирование обеих частей уравнения будет тождественным преобразованием, если обе части заведомо положительны. И так далее…
Подобные преобразования будут рассматриваться в соответствующих темах.
выразить переменную а и найти её значение при S =300, V 0 =20, t =10.
Средняя скорость лыжника (в км/ч) на дистанции в два круга рассчитывается по формуле:
где V 1 и V 2 – средние скорости (в км/ч) на первом и втором кругах соответственно. Какова была средняя скорость лыжника на втором круге, если известно, что первый круг лыжник пробежал со скоростью 15 км/ч, а средняя скорость на всей дистанции оказалась равной 12 км/ч?
Задача на основе реального варианта ОГЭ:
Задача на основе реального варианта профильного ЕГЭ:
К источнику с ЭДС ε=155 В и внутренним сопротивлением r =0,5 Ом хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, даётся формулой:
При каком сопротивлении нагрузки напряжение на ней будет 150 В? Ответ выразите в омах.
Ответы (в беспорядке): 4; 15; 2; 10.
А уж где числа, километры в час, метры, омы – это как-нибудь сами…)