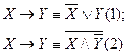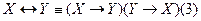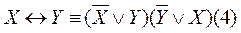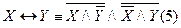Как выразить дизъюнкцию через импликацию
Как выразить дизъюнкцию через импликацию
Простые высказывания в алгебре логики обозначают заглавными латинскими буквами:
Истинному высказыванию ставится в соответствие 1, ложному – 0.
Таким образом, А = 1, В = 0.
Логическая операция конъюнкции (логическое умножение)
Конъюнкция (соединение), или логическое умножение, – логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Операция в естественном языке выражается связкой «и».
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т. е. множеству, получившемуся в результате умножения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Высказывание А ∙ В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Логическая операция дизъюнкции (логическое сложение)
Например : A | B; A || B; A or B.
Высказывание А ˅ В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Логическая операция инверсии (отрицание)
Отрицание (инверсия) – логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.
Высказывание A 
Логическая операция импликации (логическое следование)
Высказывание А → В ложно тогда и только тогда, когда А истинно, а В ложно.
Импликацию можно выразить через дизъюнкцию и отрицание:
А → В = A 
Логическая операция эквиваленция (равнозначность), или двойная импликация
В обычной речи операция эквиваленции выражается связками «тогда и только тогда», «в том и только в том случае», «необходимо и достаточно», «. равносильно. ».
Обозначается знаком ↔ или
. Высказывание А ↔ В истинно тогда и только тогда, когда значения А и В совпадают.
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию: А ↔ В = ( Ā ˅ В) ∙ (B ˅ А).
Как выразить дизъюнкцию через импликацию
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Операции над высказываниями и предикатами. Таблицы истинности
п.1. Отрицание
Расшифровка первого правила: высказывание «неверно, что для любого x выполняется A(x)» совпадает с высказыванием «найдётся x, для которого A(x) не выполняется».
Расшифровка второго правила: высказывание «неверно, что найдётся x, для которого выполняется A(x)» совпадает с высказыванием «для любого x A(x) не выполняется».
п.2. Конъюнкция
Обозначение конъюнкции A ∧ B, читается «А и В». Таблица истинности:
С точки зрения операций над множествами, конъюнкция аналогична пересечению двух множеств (см. §10 справочника для 8 класса).
С точки зрения записи условий, конъюнкция аналогична системе с фигурной скобкой.
п.3. Дизъюнкция
Обозначение дизъюнкции A ∨ B, читается «А или В». Таблица истинности:
С точки зрения операций над множествами, дизъюнкция аналогична объединению двух множеств (см. §10 справочника для 8 класса).
п.4. Импликация
Обозначение импликации A → B, читается «если A, то B».
Высказывание A называют «посылкой», а высказывание B – «заключением».
Значение импликации зависит от порядка высказываний.
Таблица истинности:
п.5. Эквиваленция
Обозначение эквиваленции A ↔ B, читается «A то же самое, что B» или «A эквивалентно B».
Таблица истинности:
п.6. Законы де Моргана
Докажем эквивалентность с помощью таблиц истинности:
Мы видим, что итоговые столбцы слева и справа полностью совпадают.
Значит, высказывания эквивалентны.
Докажем эквивалентность с помощью таблиц истинности:
Высказывания слева и справа эквивалентны.
Не путайте эквиваленцию и эквивалентность.
Эквиваленция – это логическая операция с 0 или 1 на выходе, в зависимости от исходных А и В.
Эквивалентность(равносильность) – это отношение, при котором эквиваленция A ↔ B истинна при всех значениях логических переменных на области определения. Тогда A ⇔ B (пишут также A=B, A≡B, A
B).
Если A ⇔ B, то каждое из предложений является и необходимым и достаточным условием для другого предложения; используются словосочетания «необходимо и достаточно», «равносильно».
п.7. Алгоритм доказательства эквивалентности высказываний с помощью таблиц истинности
Например:
Докажем следующее свойство:
XIII.- законы склеивания
XII.- законы поглощения.
Для сокращения и лучшей обозримости записей будем иногда опускать знак конъюнкции (так же как опускают знак умножения), условившись под выражением ХY подразумевать формулу (X/\Y). Так, например, вместо формулы (X/\У)\/Z будем иногда писать ХУ\/Z‑ запись X(Y\/Z)X нужно понимать как формулу (Х /\(Y/\Z))\/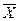
Обратим внимание на характер соответствий между равносильностями, объединенными в пары под номерами V-XIII. В этих соответствиях проявляется так называемый принцип двойственности.
Две формулы, не содержащие знаков → и ↔, называются двойственными, если каждую из ник можно получить из другой заменой /\, \/, и, л соответственно на \/, /\, л, и.
Принцип двойственности утверждает следующее: если две формулы (не содержащие знаков → и ↔) равносильны, то двойственные им формулы тоже равносильны.
Например, для формулы л двойственной является формула и, а для формулы Х/\л — формула Х\/и; убедившись, что Х/\л≡л, согласно принципу двойственности получаем равносильность Х\/и≡и.
4. Выражение импликации и эквиваленции через конъюнкцию, дизъюнкцию и отрицание. До сих пор мы занимались равносильными преобразованиями формул, не содержащих знаков → и ↔. Сейчас покажем, что всякую формулу, содержащую → или ↔ можно заменить
равносильной ей формулой, не содержащей этих знаков.
Имеют место следующие равносильности (проверьте!):
Будем говорить, что равносильность (1) выражает импликацию через дизъюнкцию и отрицание, а равносильность (2) — через конъюнкцию и отрицание.
Эквиваленция выражается через конъюнкцию и импликацию равносильностью
(проверьте!). Из равносильностей (3) и (1) получаем равносильность
выражающую эквиваленцию через конъюнкцию, дизъюнкцию и отрицание. Из равносильностей (3) и (2) получаем равносильность
выражающую эквиваленцию через конъюнкцию и отрицание.
Очевидно, что в принципе можно было бы обойтись всего двумя операциями: конъюнкцией и отрицанием.
Возникает вопрос: а нельзя ли выразить через какую-нибудь одну операцию все остальные? Можно доказать, что ни через одну из введенных здесь пяти логических операций этого сделать нельзя. Нужны, по меньшей мере, две операции; при этом одной из них обязательно должно быть отрицание.
Все остальные операции можно выразить через конъюнкцию и отрицание, дизъюнкцию и отрицание или импликацию и отрицание. Через эквиваленцию и отрицание остальные операции выразить нельзя.
Зачем же вводить пять операций, когда можно обойтись двумя? Напомним, что введенные пять операций соответствуют наиболее употребительным союзам. Использование лишь двух операций усложнило бы формализацию предложений естественного языка и привело 6ы к громоздким, труднообозримым формулам. В других приложениях математической логики эти доводы в пользу введения и употребления всех пяти операций теряют силу; там ограничиваются меньшим числом операций. Аналогичное положение имеет место в арифметике: всякое число может быть записано с помощью двух цифр: 0 и 1; однако, поскольку записи чисел и выкладок в двоичной системе счисления очень громоздки, мы прибегаем к этой системе лишь в специальных случаях.
Можно ввести логическую операцию, через которую выражаются все пять операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция. Такова, например, операция, соответствующая сложному союзу «не A или не B» («или» — неразделительное). Эта операция обозначается символом | (например, А|В) и получила название штрих Шеффера. Штрих Шеффера определяется с помощью такой таблицы:
| X | Y | Х|Y |
| и | и | л |
| и | л | и |
| л | и | и |
| л | л | и |
Непосредственно из таблицы видно, что Х|У≡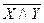
Легко убедиться (сделайте это!), что Х|Х≡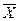
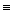
Таким образом, нам удалось выразить через штрих Шеффера отрицание и конъюнкцию, а через них, в свою очередь, можно выразить дизъюнкцию, импликацию и эквиваленцию.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Как выразить дизъюнкцию через импликацию

2. Построение таблиц истинности и логических функций.
3. Законы логики и преобразование логических выражений.
Лабораторная работа № 3. Основы математической логики.

Исследования в алгебре логики тесно связаны с изучением высказываний (хотя высказывание — предмет изучения формальной логики). Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности (Аристотель).
Простым высказыванием называют повествовательное предложение, относительно которого имеет смысл говорить, истинно оно или ложно.
Считается, что каждое высказывание либо истинно, либо ложно и ни одно высказывание не может быть одновременно истинным и ложным.
Высказывания 1 и 3 являются истинными. Высказывание 2 – ложным , потому что число 27 составное 27=3*3*3.
Итак, отличительным признаком высказывания является свойство быть истинным или ложным, последние четыре предложения этим свойством не обладают.
С помощью высказываний устанавливаются свойства, взаимосвязи между объектами. Высказывание истинно, если оно адекватно отображает эту связь, в противном случае оно ложно.
Однако определение истинности высказывания далеко не простой вопрос. Например, высказывание «Число 1 +22 = 4294 967297 — простое», принадлежащее Ферма (1601-1665), долгое время считалось истинным, пока в 1732 году Эйлер (1707-1783) не доказал, что оно ложно. В целом, обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания «Сумма углов треугольника равна 180°» устанавливается геометрией, причем в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные, большими буквами латинского алфавита.
Существуют разные варианты обозначения истинности и ложности логических переменных:
Сложные (составные) высказывания представляют собой набор простых высказываний (по крайней мере двух) связанных логическими операциями.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой (логическим выражением).
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
Введем перечисленные логические операции.
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.