Как выразить косинус в градусах
Как найти синус и косинус углов в градусах без тригонометрической таблицы?
В статье мы расскажем, как находить значения:
Как вычисляются синусы и косинусы углов?
Предположим, стоит задача найти косинус и синус угла \(30^°\). Отложим на круге угол в \(30^°\) и найдем какая точка соответствует этому углу.
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают \(0,1\); \(0,2\); \(0,3\) и т.д., а сразу наносят стандартные значения для синуса и косинуса: \(±\frac<1><2>=±0,5\); \(±\frac<\sqrt<2>> <2>≈±0,707\); \(±\frac<\sqrt<3>> <2>≈±0,866\).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
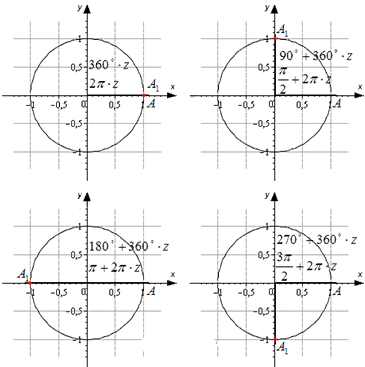
Как отметить любой угол на тригонометрическом круге?
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
Градусная мера окружности равна \(360^°\), полуокружности \(180^°\), а четверти \(90^°\);
Углы в \(0^°\), \(30^°\), \(45^°\) и \(60^°\) выглядят так:
Задание 1 . Отметьте на окружности точки соответствующие углам: \(720^°\), \(225^°\), \(300^°\), \(870^°\), \(900^°\), \(-330^°\), \(-630^°\), \(-210^°\).
Как находить синус и косинус любого угла?
\(-540^°\) на тригонометрическом круге совпадает с \(-1\) на оси косинусов. То есть, координаты этой точки: \((-1;0)\). Значит, \(\cos(-540^°)=-1\), а \(\sin(-540^° )=0\).
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).
Примеры вычисления синуса и косинуса из ЕГЭ
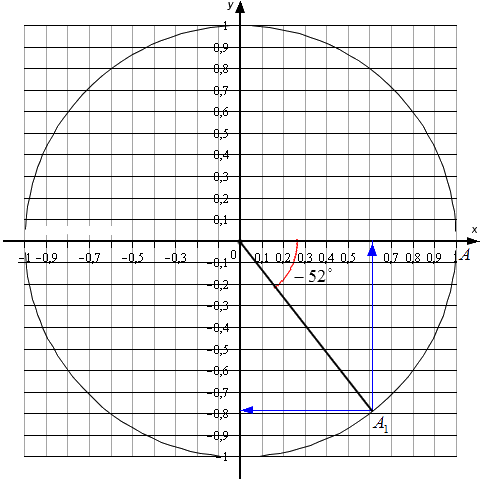
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения \(54\sqrt<3>\cos(510^°)\).
Решение. \(510^°=360^°+150^°=360^°+180^°-30^°.\)
Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
Формулы понижения степени
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы произведения тригонометрических функций
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Нахождение значений синуса, косинуса, тангенса и котангенса
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
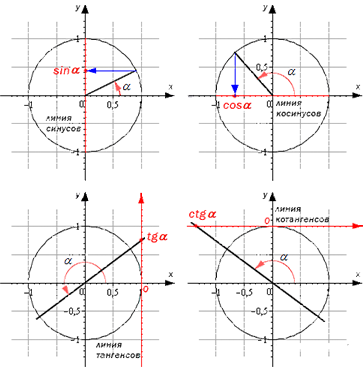
Линии тригонометрических функций
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
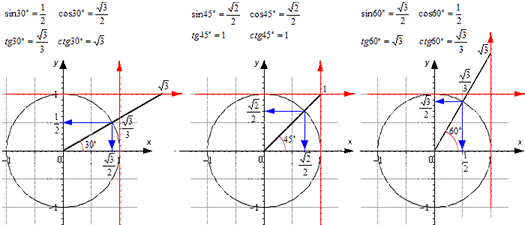
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Сведение к углу
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90 ° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Таблицы значений синусов, косинусов, тангенсов, котангенсов (sin, cos, tg, ctg)
Исходя из определений синуса, косинуса, тангенса и котангенса можно найти значения этих функций для углов 0 и 90 градусов
Значения синусов, косинусов, тангенсов и котангенсов в курсе геометрии определяются как соотношения сторон прямоугольного треугольника, углы которого равны 30, 60 и 90 градусов, и также 45, 45 и 90 градусов.
Определение тригонометрических функуций для острого угла в прямоугольном треугольнике
В соответствии с определениями находятся значения функций:
Сведем эти значения в таблицу и назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.
Таблица основных значений синусов, косинусов, тангенсов и котангенсов
Таблица синусов, косинусов, тангенсов и котангенсов
Периодичность синуса, косинуса, тангенса и котангенса позволяет расширять эту таблицу до сколь угодно больших значений углов. Значения, собранные в таблице, используются при решении задач чаще всего, поэтому их рекомендуется выучить наизусть.
Как пользоваться таблицей основных значений тригонометрических функций
Принцип пользования таблицей значений синусов, косинусов, тангенсов и котангенсов понятен на интуитивном уровне. Пересечение строки и столбца дает значение функции для конкретного угла.
Пример. Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов
Нужно узнать, чему равен sin 7 π 6
Таблицы Брадиса
Таблица Брадиса позволяет вычислить значение синуса, косинуса, тангенса или котангенса с точностью до 4-х знаков после запятой без использования вычислительной техники. Это своего рода замена инженерному калькулятору.
Таблица Брадиса для синусов и косинусов
| sin | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | cos | 1′ | 2′ | 3′ |
| 0.0000 | 90° | ||||||||||||||
| 0° | 0.0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0.0872 | 85° | 3 | 6 | 9 |
| 5° | 0.0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.1736 | 80° | 3 | 6 | 9 |
| 10° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.2588 | 75° | 3 | 6 | 8 |
| 15° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.3420 | 70° | 3 | 5 | 8 |
| 20° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0.4226 | 65° | 3 | 5 | 8 |
| 25° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.5000 | 60° | 3 | 5 | 8 |
| 30° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.5736 | 55° | 2 | 5 | 7 |
| 35° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.6428 | 50° | 2 | 4 | 7 |
| 40° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.7071 | 45° | 2 | 4 | 6 |
| 45° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.7660 | 40° | 2 | 4 | 6 |
| 50° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 54° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.8192 | 35° | 2 | 3 | 5 |
| 55° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.8660 | 30° | 1 | 3 | 4 |
| 60° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.9063 | 25° | 1 | 3 | 4 |
| 65° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22° | 1 | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.9397 | 20° | 1 | 2 | 3 |
| 70° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.9659 | 15° | 1 | 2 | 2 |
| 75° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.9848 | 10° | 1 | 1 | 2 |
| 80° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5° | 0 | 1 | 1 |
| 85° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| sin | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | cos | 1′ | 2′ | 3′ |
Для нахождения значений синусов и косинусов углов, не представленных в таблице, необходимо использовать поправки.
Теперь приведем таблицу Брадиса для тангенсов и котангенсов. Она содержит значения тангенсов углов от 0 до 76 градусов, и котангенсов углов от 14 до 90 градусов.
Таблица Брадиса для тангенса и котангенса
| tg | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | ctg | 1′ | 2′ | 3′ |
| 0 | 90° | ||||||||||||||
| 0° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87° | 3 | 6 | 9 |
| 3° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86° | 3 | 6 | 9 |
| 4° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85° | 3 | 6 | 9 |
| 5° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84° | 3 | 6 | 9 |
| 6° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83° | 3 | 6 | 9 |
| 7° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82° | 3 | 6 | 9 |
| 8° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81° | 3 | 6 | 9 |
| 9° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80° | 3 | 6 | 9 |
| 10° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79° | 3 | 6 | 9 |
| 11° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78° | 3 | 6 | 9 |
| 12° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77° | 3 | 6 | 9 |
| 13° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76° | 3 | 6 | 9 |
| 14° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75° | 3 | 6 | 9 |
| 15° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74° | 3 | 6 | 9 |
| 16° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73° | 3 | 6 | 9 |
| 17° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72° | 3 | 6 | 10 |
| 18° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71° | 3 | 6 | 10 |
| 19° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70° | 3 | 7 | 10 |
| 20° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69° | 3 | 7 | 10 |
| 21° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68° | 3 | 7 | 10 |
| 22° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67° | 3 | 7 | 10 |
| 23° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66° | 3 | 7 | 10 |
| 24° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65° | 4 | 7 | 11 |
| 25° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64° | 4 | 7 | 11 |
| 26° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63° | 4 | 7 | 11 |
| 27° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62° | 4 | 7 | 11 |
| 28° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61° | 4 | 8 | 11 |
| 29° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60° | 4 | 8 | 12 |
| 30° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59° | 4 | 8 | 12 |
| 31° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58° | 4 | 8 | 12 |
| 32° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57° | 4 | 8 | 12 |
| 33° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56° | 4 | 8 | 13 |
| 34° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55° | 4 | 9 | 13 |
| 35° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54° | 4 | 8 | 13 |
| 36° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53° | 5 | 9 | 14° |
| 37° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52° | 5 | 9 | 14 |
| 38° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51° | 5 | 9 | 14 |
| 39° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50° | 5 | 10 | 15 |
| 40° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49° | 5 | 10 | 15 |
| 41° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48° | 5 | 10 | 16 |
| 42° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47° | 6 | 11 | 16 |
| 43° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46° | 6 | 11 | 17 |
| 44° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45° | 6 | 11 | 17 |
| 45° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44° | 6 | 12 | 18 |
| 46° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43° | 6 | 12 | 18 |
| 47° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42° | 6 | 13 | 19 |
| 48° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41° | 7 | 13 | 20 |
| 49° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40° | 7 | 14 | 21 |
| 50° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39° | 7 | 14 | 22 |
| 51° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38° | 8 | 15 | 23 |
| 52° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37° | 8 | 16 | 24 |
| 53° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36° | 8 | 16 | 25 |
| 54° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35° | 9 | 17 | 26 |
| 55° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34° | 9 | 18 | 27 |
| 56° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33° | 10 | 19 | 29 |
| 57° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32° | 10 | 20 | 30 |
| 58° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31° | 11 | 21 | 32 |
| 59° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30° | 11 | 23 | 34 |
| 60° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1,804 | 29° | 1 | 2 | 4 |
| 61° | 1,804 | 1,811 | 1,819 | 1,827 | 1,834 | 1,842 | 1,849 | 1,857 | 1,865 | 1,873 | 1,881 | 28° | 1 | 3 | 4 |
| 62° | 1,881 | 1,889 | 1,897 | 1,905 | 1,913 | 1,921 | 1,929 | 1,937 | 1,946 | 1,954 | 1,963 | 27° | 1 | 3 | 4 |
| 63° | 1,963 | 1,971 | 1,980 | 1,988 | 1,997 | 2,006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26° | 1 | 3 | 4 |
| 64° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25° | 2 | 3 | 5 |
| 65° | 2,145 | 2,154 | 2,164 | 2,174 | 2,184 | 2,194 | 2,204 | 2,215 | 2,225 | 2,236 | 2,246 | 24° | 2 | 3 | 5 |
| 66° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23° | 2 | 4 | 5 |
| 67° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22° | 2 | 4 | 6 |
| 68° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2,605 | 21° | 2 | 4 | 6 |
| 69° | 2,605 | 2,619 | 2,633 | 2,646 | 2,66 | 2,675 | 2,689 | 2,703 | 2,718 | 2,733 | 2,747 | 20° | 2 | 5 | 7 |
| 70° | 2,747 | 2,762 | 2,778 | 2,793 | 2,808 | 2,824 | 2,840 | 2,856 | 2,872 | 2,888 | 2,904 | 19° | 3 | 5 | 8 |
| 71° | 2,904 | 2,921 | 2,937 | 2,954 | 2,971 | 2,989 | 3,006 | 3,024 | 3,042 | 3,06 | 3,078 | 18° | 3 | 6 | 9 |
| 72° | 3,078 | 3,096 | 3,115 | 3,133 | 3,152 | 3,172 | 3,191 | 3,211 | 3,230 | 3,251 | 3,271 | 17° | 3 | 6 | 10 |
| 73° | 3,271 | 3,291 | 3,312 | 3,333 | 3,354 | 3,376 | 3 | 7 | 10 | ||||||
| 3,398 | 3,42 | 3,442 | 3,465 | 3,487 | 16° | 4 | 7 | 11 | |||||||
| 74° | 3,487 | 3,511 | 3,534 | 3,558 | 3,582 | 3,606 | 4 | 8 | 12 | ||||||
| 3,630 | 3,655 | 3,681 | 3,706 | 3,732 | 15° | 4 | 8 | 13 | |||||||
| 75° | 3,732 | 3,758 | 3,785 | 3,812 | 3,839 | 3,867 | 4 | 9 | 13 | ||||||
| 3,895 | 3,923 | 3,952 | 3,981 | 4,011 | 14° | 5 | 10 | 14 | |||||||
| tg | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | ctg | 1′ | 2′ | 3′ |
Как пользоваться таблицами Брадиса
Для нахождения значений синуса угла нужно найти пересечение строки, содержащей в крайней левой ячейке необходимое количество градусов, и столбца, содержащего в верхней ячейке необходимое число минут.
Если точного значения угла нет в таблице Брадиса, прибегаем к помощи поправок. Поправки на одну, две и три минуты даны в крайних правых столбцах таблицы. Для нахождения значения синуса угла, которого нет в таблице, находим самое близкое к нему значение. После этого прибавляем или отнимаем поправку, соответствующую разнице между углами.
Пример. Как пользоваться таблицей Брадиса
Принцип работы с косинусами, тангенсами и котангенсами аналогичен. Однако, важно помнить о знаке поправок.
При вычислении значений синусов поправка имеет положительный знак, а при вычислении косинусов поправку необходимо брать с отрицательным знаком.