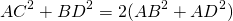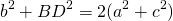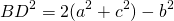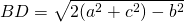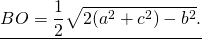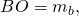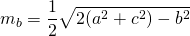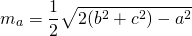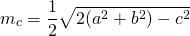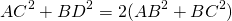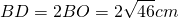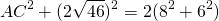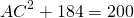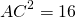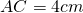Как выразить медиану через стороны треугольника

Элементы треугольника. Медиана

Определение

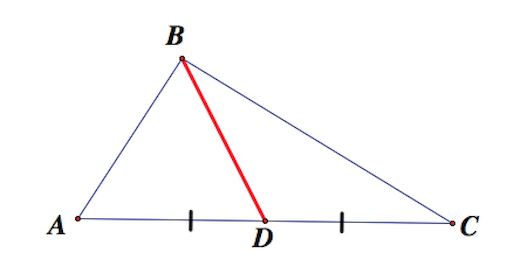
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Свойства

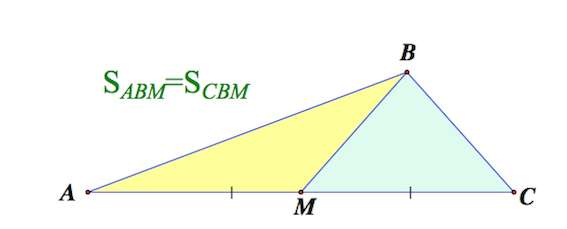
2. Медиана треугольника делит его на два треугольника равной площади (равновеликих треугольника)

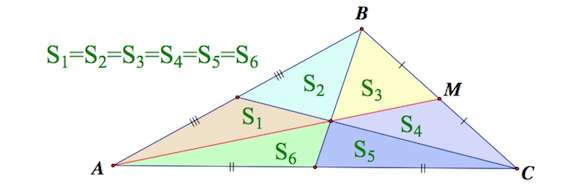
3. Медианы треугольника делят треугольник на 6 равновеликих треугольников

4. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы

5. Длина медианы треугольника вычисляется по формуле:

, где где — медиана к стороне ; — стороны треугольника

6. Длина стороны треугольника через медианы вычисляется по формуле:

, где – медианы к соответствующим сторонам треугольника, — стороны треугольника.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Определение и свойства медианы треугольника

В данной статье мы рассмотрим определение медианы треугольника, перечислим ее свойства, а также разберем примеры решения задач для закрепления теоретического материала.

Определение медианы треугольника

Медиана – это отрезок, соединяющий вершину треугольника с серединой стороны, расположенной напротив данной вершины.

Основание медианы – точка пересечения медианы со стороной треугольника, другими словами, середина этой стороны (точка F).

Свойства медианы

Свойство 1 (основное)

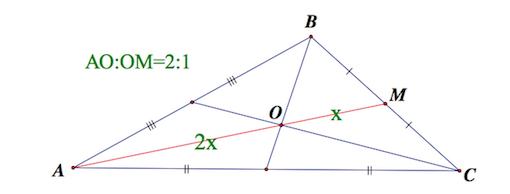
Т.к. в треугольнике три вершины и три стороны, то и медиан, соответственно, тоже три. Все они пересекаются в одной точке (O), которая называется центроидом или центром тяжести треугольника.

В точке пересечения медиан каждая из них делится в отношении 2:1, считая от вершины. Т.е.:

Свойство 2

Медиана делит треугольник на 2 равновеликих (равных по площади) треугольника.

Свойство 3

Три медианы делят треугольник на 6 равновеликих треугольников.

Свойство 4

Наименьшая медиана соответствует большей стороне треугольника, и наоборот.

Свойство 5

Допустим, известны все стороны треугольника (примем их за a, b и c).

Длину медианы m_a, проведенную к стороне a, можно найти по формуле:

Примеры задач

Задание 2
Стороны треугольника равны 6, 8 и 10 см. Найдите медиану, проведенную к стороне с длиной 6 см.

Решение
Воспользуемся формулой, приведенной в свойстве 5:

Источник

По сторонам треугольника найти его медиану

Рассмотрим задачу, в которой требуется по сторонам треугольника найти его медиану.

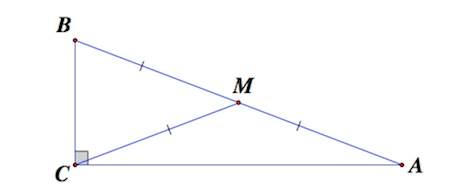
Даны стороны треугольника. Найти длину медианы, проведенной к наибольшей стороне.

Дано: ∆ ABC,

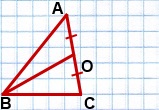
сторона AC — наибольшая,

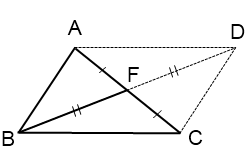
1) На луче BO отложим отрезок OD, OD=BO.

2) Проведем отрезки AD и CD.

3) Рассмотрим четырехугольник ABCD.

AO=CO (так как BO — медиана треугольника ABC по условию);

BO=DO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

так как BO=1/2 BD (по построению),

Если ввести обозначение

формула для нахождения медианы треугольника по его сторонам примет вид:

Запоминать эту формулу не обязательно. При решении конкретной задачи следует привести все рассуждения.

Если медиана проведена не к наибольшей, а к наименьшей либо средней по величине стороне, решение задачи аналогично.

Соответственно, формулы для нахождения длины медианы в этих случаях:

Приём, который применили для решения задачи — метод удвоения медианы.

Источник

Узнать ещё

Знание — сила. Познавательная информация

По сторонам и медиане найти сторону треугольника

Чтобы по сторонам и медиане найти сторону треугольника, достаточно знать ход решения задачи. Учить дополнительную формулу не обязательно.

Сначала рассмотрим, как по сторонам и медиане найти сторону треугольника, в общем виде.

Пусть в треугольнике ABC известны стороны AB=c, AC=b и медиана BF=m.

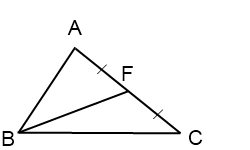
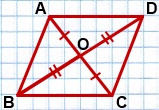
На луче BF отложим отрезок FD, FD=BF и соединим точку D с точками A и C.

Поскольку в полученном четырехугольнике ABCD диагонали точкой пересечения делятся пополам, то ABCD — параллелограмм (по признаку). А значит, мы можем применить свойство диагоналей параллелограмма: сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Имеем: AC²+BD²=2(AB²+BC²). Отсюда b²+(2m)²=2(c²+BC²), b²+4m²=2c²+2BC², BC²=(b²+4m²-2c²)/2.

Переходим к решению конкретной задачи.

По двум сторонам 6 см и 8 см и медиане,проведенной к третьей стороне, найти неизвестную сторону треугольника. Длина медианы равна √46 см.

Пусть AB=6 см, BC=8 см, BF=√46 см. Рассуждая аналогично, получаем: AC²+BD²=2(AB²+BC²), AC²+(2√46)²=2(6²+8²), AC²+4∙46=200, AC²=200-184=16, AC=4 см.

Источник

Найти сторону треугольника через медиану и стороны

Найти сторону треугольника через медиану и стороны — задача, обратная нахождению медианы через стороны.

Решается она аналогично, то есть с помощью дополнительного построения и применения свойства диагоналей параллелограмма.

Стороны треугольника равны 6 см и 8 см. Медиана, проведенная к его третьей стороне, равна √46 см. Найти неизвестную сторону треугольника.

BO — медиана, BO=√46 см.

1) На луче BO отложим отрезок OD,

2) Соединим точку D с точками A и C.

3) AO=CO (так как BO — медиана по условию), OD=BO (по построению).

Так как диагонали четырехугольника ABCD в точке пересечения делятся пополам, то ABCD — параллелограмм (по признаку).

Если ввести обозначения BC=a, AB=c, AC=b, BO=mb, то получим формулу для нахождения стороны треугольника через медиану и две другие стороны:

Источник