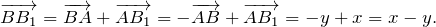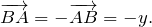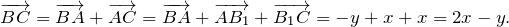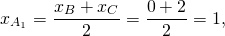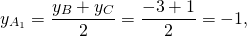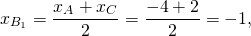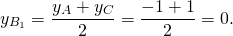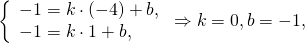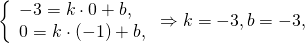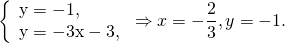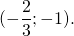Как выразить медиану через векторы
Как найти медиану треугольника в векторах?
Известно, что |p| = 3; |q| = 1; угол (p, q) = pi/3.
1) Найти скалярное произведение p*q. Это я примерно знаю, как сделать, но хочу послушать ваше мнение.
2) Выразить вектор BC через p и q, по возможности найти длину BC.
Можете помочь решить?
1. Скалярное произведение векторов p и q.
= |p|*|q|*cos(p,q) = 3 * 1 * 1/2 = 1,5
2. Выразить вектор BC через p и q, найти его длину.
Чтобы найти длину используем теорему косинусов:
|ВС| = 3
3. Найти медиану АМ и её длину.
И снова теорема косинусов:
|AM| = 7,5
Вот примерно так. Обращайтесь, если что-то не так.
Ответ на первый ответ постой:
Скалярное произведение есть скаляр, равный произведению модулей на косинус угла между ними:
А=|p|*|q|*cos(p, q) = 3 *1* cos (pi/3) = 3*0,5=1,5..
Со вторыми заданиями немного сложнее:
Сначала установим условно вектор q на оси х, тогда получим, что оба вектора начинаются в 0 и имеют между собой заданный угол..
Разложим оба вектора p и q на взаимно ортогональные составляющие:
Итак, мы задали точку А(0;0), получили точки В(2;5,2) С(6,5;4,5)..
Вектор ВС задаётся точкой А и В..
Теперь всё просто: находим длину отрезка ВС по известным координатам:
отношение cos a=(5,2-4,5)/4,5 есть угол относительно оси абсцисс, относительно которой мы и отсчитываем угол а=81 град=1,41 рад..
Модуль и угол задают вектор ВС..
Чтобы найти длину медианы нужно найти точку М, которая делит ВС напополам 4,5/2 = 2,25..
Из подобия прямоугольного треугольника, построенного на точек М стороны
Это координаты точки М (4,25;4,85)..
Теперь находим АМ=sqrt((4,25)^2+(4,85)^2)=6,45..
Это и есть искомая длина медианы..
У меня есть подозрение, что теорема косинусов неприменима в том виде, как её использовали в предложенных решениях. Сомнения насчёт взятых косинусов. Проверим непосредственно с помощью скалярных произведений полученных векторов. Считаем, что ищем диагонали параллелограмма ABDC.
Но вот дальше используем только скалярное произведение
2) BC=AC-AB=3p+2q-2p+q=p+3q. А теперь найдём |BC| не по теореме косинусов.
3) AD=AB+AC=5p+q, AD^2=(5p+q)*(5p+q)=25p^2+10pq+q^2=25*9+15+1=241, AD=корень(241), AM=0,5*корень(241)
И чтобы ещё раз озадачить тех, кто сомневается в применимости этого метода, прилагаю рисунок с решением аналогичной задачи
Отрезок ВВ1 медиана треугольника ABC выразите векторы
Здравствуйте!
Нужно разобраться с решением задачи:
Отрезок ВВ1 – медиана треугольника ABC. Выразите векторы B1C, ВВ1, ВА, ВС через вектор х =АВ1 и вектор у=АВ.
Буду благодарна за помощь!
Спасибо!
Задача.
Отрезок ВВ1 — медиана треугольника ABC. Выразите векторы B1C, ВВ1, ВА, ВС через вектор х =АВ1 и вектор у=АВ.
Решение.
Построим треугольник АВС.
Проведем в нем из вершины В медиану ВВ1. 
По условию задачи 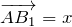
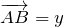
Нужно найти векторы В1С, ВВ1, ВА и ВС через заданные векторы.
Поскольку ВВ1 — медиана треугольника АВС, поэтому АВ1 = В1С.
Вектор 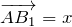
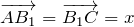
Рассмотрим треугольник АВВ1.
По правилу треугольника найдем вектор ВВ1:
Найдем вектор ВА:
Векторы АВ и ВА одинаковой длины, но противоположных направлений, поэтому:
Рассмотрим треугольник АВС.
По правилу треугольника найдем вектор ВС:
Ответ. 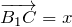
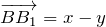
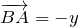
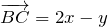
При решении упоминалось о равных векторах, но противоположных по направлению.
Так вот, два вектора, которые имеют равные модули (то есть одинаковые длины) и направленные в противоположные стороны, называют противоположными.
Например, вектор КМ будет противоположным вектору МК, так как длины их одинаковые, а вот направлены они в противоположные стороны.
Это важно только при решении задач на векторы. В геометрии отрезок КМ и отрезок МК будут абсолютно равными, так как в геометрии не принято учитывать направление, а только длину.
Точка пересечения медиан треугольника
Как найти точку пересечения медиан треугольника, зная координаты его вершин?
Поскольку все медианы треугольника пересекаются в одной точке, достаточно составить уравнения двух медиан и найти координаты их точки пересечения.
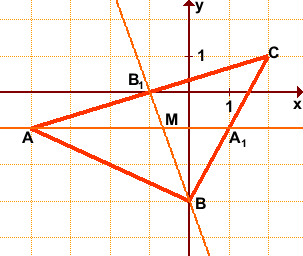
Найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1).
Обозначим середины сторон BC и AC через A1 и B1 соответственно. По формулам координат середины отрезка
Составим уравнения медиан AA1 и BB1.
Уравнение медианы AA1 можно найти как уравнение прямой, проходящей через две точки A(-4;-1) и A1(1;-1).
B(0;-3), B1(-1;0). Найдём уравнение медианы BB1.
Координаты точки пересечения прямых AA1 и BB1 ищем как решение системы уравнений
Поскольку все медианы медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины, можно найти координаты концов любой медианы, а затем точку, которая делит медиану в отношении 2:1, начиная отсчёт от точки, которая является вершиной треугольника.
Например, в условиях предыдущей задачи — найти координаты точки пересечения медиан треугольника с вершинами в точках A(-4;-1), B(0;-3), C(2;1), —
зная координаты A1(1;-1), найдём координаты точки M. Точка M пересечения медиан треугольника делит отрезок AA1 в отношении 2:1, считая от точки A.