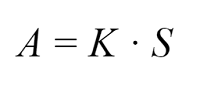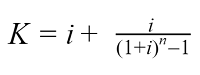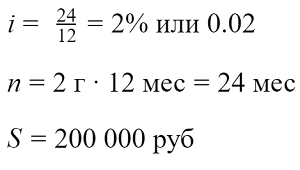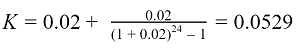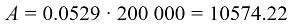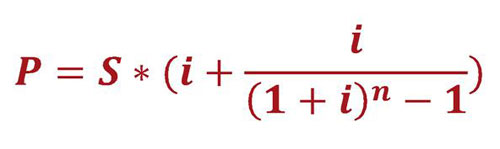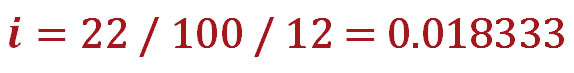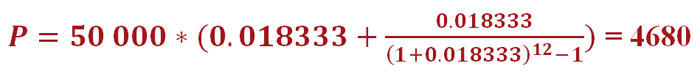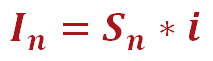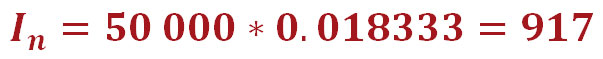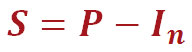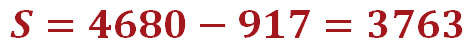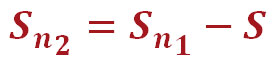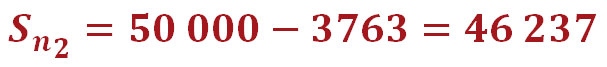Как вывести формулу аннуитетного платежа

Аннуитет по кредиту — что это?

Тенденции развития современного общества привели к тому, что те понятия, которые не так давно использовались главным образом в учебниках по экономической теории, стали все чаще встречаться в повседневной жизни. Одним из таких терминов является аннуитет, который все более активно стали использовать в сфере кредитования. Данный инструмент является достаточно выгодным, поэтому есть смысл познакомиться с его отличительными особенностями и способами расчета более подробно. Об этом и пойдет речь в данной статье.

Что такое аннуитет?

По аннуитетному виду платежа предполагается что выплаты осуществляются равными суммами через равные промежутки времени. Сумма аннуитетного платежа состоит из двух частей:

Аннуитет позволяет сделать величину платежа, который включает в себя не только проценты за период, но и часть основного долга, постоянной. Это дает возможность плательщику заранее оценить свои силы и запланировать выплаты определенной суммы денежных средств в течение оговоренного срока.

Основным отличием от так называемого дифференцированного платежа является то, что при использовании последнего в первую очередь выплачивается полная сумма начисленных за использование кредитных средств процентов, а потом уже основной долг.

Отметим, что принцип аннуитета используется не только в кредитовании, но и для лизинговых платежей.

Какие выделяют виды аннуитета?

Для лучшего понимания использования аннуитета следует рассмотреть, какие его виды существуют. Так, можно отметить наличие следующей классификации:

Если говорить об аннуитете, используемом в сфере кредитования, то здесь имеет место отложенный аннуитет.

Кроме этого, распространенно выделение различных видов стоимости аннуитета, а именно:

Такое деление обусловлено стремлением определить максимально объективную ценность денежных средств, которые направлены на кредитование. Как будущая, так и текущая стоимость аннуитета рассчитывается определенным образом с использованием конкретных формул. Проводимый расчет текущей стоимости аннуитета зависит от ряда факторов.

Стоит отметить, что в силу теории о том, что с течением времени денежные средства могут обесцениваться в силу инфляции, имеет место такое понятие, как настоящая стоимость аннуитета. Также здесь играет роль упущенная выгода, ведь если бы кредитор оставил выданные денежные средства у себя, то он имел бы возможность получать доход в виде процентов по вкладу.

Формула расчета аннуитетного платежа

Формула аннуитетного платежа:

Расчет коэффициента аннуитета:

Знание рассмотренной формулы позволяет провести требуемые расчеты, которые при наличии полных исходных данных не представляют собой особых сложностей. Очевидно, что для применения ее на практике необходимо учитывать некоторые принципиальные моменты. В их числе можно отметить, в первую очередь, принцип, по которому определяются доли основного долга и начисленных процентов в итоговом размере платежа. Для этого применяется определенная методика, которая предполагает прохождение несколько этапов расчета. Мы не будем на ней подробно останавливаться, отметим лишь общий принцип, в соответствии с которым производится расчет размера процентов и аннуитетного платежа, так же как и основного долга в виде разницы между этими двумя величинами для каждого месяца периода. При этом учитывается, что размер основного долга от месяца к месяцу снижается. Последний платеж требует отдельной корректировки в силу применения в процессе расчетов округлений.

Несмотря на равную величину платежей, соотношение суммы основного долга и начисленных процентов в их составе меняется. Если в начале основная доля приходится на проценты, то ближе к концу выплат остается погасить главным образом основную сумму долга.

Пример расчета аннуитетного платежа

Рассчитаем ежемесячный платеж по кредиту с аннуитетным графиком погашения под процентную ставку 24% годовых сроком на 2 года и на сумму 200 000 рублей.

Воспользуемся приведенными выше формулами:

Рассчитаем коэффициент аннуитета:

Теперь мы можем приступить к расчеты самого ежемесячного платежа. Подставим полученное значение коэффициента аннуитета:

Сумма ежемесячного платежа составила 10574.22 рублей.

Переплата по кредиту

Всего за 2 года банку будет выплачено 253 781.3 руб (10574.22 руб умноженные на 24 мес), а переплата составит 53781.3 руб.

Рассчитать кредит можно с помощью калькулятора кредита на нашем сайте.

Источник

Аннуитетный платёж

Аннуитетный платёж – это платёж, который устанавливается в равной сумме через равные промежутки времени. Так, при аннуитетном графике погашения кредита вы ежемесячно платите одну и ту же сумму, независимо от остатка задолженности. Другим способом внесения ежемесячных платежей является дифференцированный способ погашения.

Для сравнения, при дифференцированной схеме погашения кредита сумма основного долга выплачивается ежемесячно равными долями, а проценты рассчитываются от остатка задолженности. В таком случае сумма ежемесячного платежа уменьшается в процессе погашения кредита.

Например, сумма процентов за первый месяц пользования кредитом равна:

S%1 = S * i,

где S%1 – сумма процентов за первый месяц,

За второй и следующие месяцы:

где ∆S – сумма погашенного основного долга.

Как рассчитать ежемесячный платёж?

Формула расчёта суммы ежемесячного платежа при аннуитетной схеме погашения следующая:

A = K * S

где А – сумма ежемесячного аннуитетного платежа,

Сумма кредита известна. А для расчёта К – коэффициента аннуитета, используется следующая формула:

Применив вышеописанную схему расчёта, вы сможете узнать сумму, которую необходимо будет погашать ежемесячно.

Пример расчёта аннуитетного платежа

Предположим, что нужно провести расчёт ежемесячного платежа по кредиту с аннуитетным графиком погашения под процентную ставку 48% годовых сроком на 4 года на сумму 2 000 рублей. Используя приведённую выше формулу расчёта ежемесячного платежа (A = K • S) и коэффициента К, рассчитаем аннуитетный платёж.

Имеем:

i= 48%/12 месяцев = 4% или 0,04

n = 4 года* 12 месяцев = 48 (месяцев)

Рассчитываем К:

А теперь подставим полученное значение в формулу ежемесячного платежа:

А = 0,0472 * 2 000 = 94,4 рублей.

Таким образом, в течение 4 лет (или 48 месяцев) необходимо будет вносить в банк платёж в сумме 94,4 рублей. Переплата по кредиту за 4 года составит 2 531,2 ( = 94,4 * 48 – 2 000).

Кому выгоден аннуитет?

В первую очередь аннуитетный способ погашения выгоден банку. Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита. При дифференцированной графике уплата процентов за 100% суммы кредита происходит только в первом месяце (в случае отсутствия отсрочки уплаты основного долга), далее проценты начисляются на остаток, из-за чего итоговая переплата по кредиту окажется меньше. Иными словами, среди двух кредитов с одинаковыми процентными ставками, сроком погашения и дополнительными комиссиями, кредит с аннуитетной схемой погашения всегда будет дороже.

Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 1 960 рублей. Это на 571,2 рубля меньше, чем при аннуитетной схеме.

С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю, так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса, в то время как при дифференцированном графике каждый месяц сумма платежа окажется разной.

Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.

Источник

Банковский кредит. Аннуитетный платеж

Аннуитетный платеж – это такая система выплат, при которой кредит выплачивается ежегодно (ежемесячно) равными платежами.
При этом каждый год (месяц) до внесения платежа банк начисляет на оставшуюся часть долга некоторый процент, то есть оставшаяся сумма долга увеличивается на это количество процентов.

Пример 1. Клиент взял в банке \(500\,000\) рублей под \(5\%\) годовых. Сколько рублей он будет должен банку в конце первого года?

\(\dfrac<105><100>\cdot 500\,000=1,05\cdot 500\,000=525\,000\) рублей.

Пример 2. Клиент взял \(2,1\) млн рублей в банке под \(10\%\) годовых и должен погасить кредит через \(2\) года равными ежегодными платежами. Сколько рублей должен составлять его ежегодный платеж?

Отсюда находим ежегодный платеж \(x=1,21\) млн рублей.

Не забываем перевести сумму из тыс.руб. в рубли.
Таким образом, клиент может взять в банке \(136\,000\) рублей.

Пример 4. Михаил взял в банке \(488\,000\) рублей на \(3\) года. В банке ему сказали, что выплачивать кредит он должен, внося каждый год платеж в размере \(250\,000\) рублей, но забыли сообщить о процентной ставке банка. Помогите Михаилу определить, какой процент начисляет банк раз в год на сумму долга?

Значит, уравнение принимает вид \((4t-5)(61t^2+45t+25)=0\)
Уравнение \(61t^2+45t+25=0\) не имеет корней.

Выведем общую формулу для аннуитетных платежей. Уже по уравнениям из предыдущих примеров должно стать понятно, как она выглядит. Но все же приведем ее вывод.

Вывод формулы:

Таким образом, \(t(t^A-t^x-\dots-x)-x=0 \Rightarrow t^nA-x(t^+t^+\dots+1)=0\)

Значит, в случае с аннуитетным платежом имеет место следующая формула: \[<\large<\left(\frac<100+r><100>\right)^n\cdot A-x\left(\left(\frac<100+r><100>\right)^+\left(\frac<100+r><100>\right)^+\dots+1\right)=0>>\] где \(A\) – сумма, взятая в кредит, \(r\%\) – процентная ставка в банке, \(x\) – сумма платежа, \(n\) – количество лет (месяцев), на которое взят кредит.

Задачи из сферы финансовой математики на расчет аннуитетного платежа по кредиту с применением формул сравнительно недавно были добавлены во вторую часть ЕГЭ. В связи с этим старшеклассникам, которые готовятся к прохождению аттестационного испытания, непременно стоит научиться справляться с подобными заданиями. Для того чтобы правильно рассчитать аннуитетный платеж, учащиеся должны уметь применять навыки анализа числовых данных и работать с формулами. Разобравшись с базовой теорией, учащиеся смогут оперативно решать задачи с любым количеством действий. Все это позволит будущим студентам рассчитывать на получение конкурентных баллов по итогам сдачи экзамена.

Как подготовиться к ЕГЭ?

Часто найти весь необходимый материал оказывается достаточно проблематично. В нужный момент школьного учебника может попросту не оказаться под рукой. А формула расчета аннуитетного платежа по кредиту во многих источниках представлена без соответствующих объяснений.

Вместе с образовательным порталом «Школково» учащиеся смогут качественно подготовиться к прохождению аттестационного испытания. Формула размера аннуитетного платежа и другой базовый материал подобран и систематизирован нашими специалистами на основе богатого опыта в максимально доступной форме. Изучив основы теории, учащиеся смогут восполнить пробелы в знаниях.

Для качественной подготовки к сдаче экзамена выпускникам необходимо не только вспомнить основной материал, но и обязательно попрактиковаться в решении задач, в которых применяется формула процента по аннуитетному платежу. Большая подборка подобных упражнений представлена в разделе «Каталог». Все задания, в которых применяется формула расчета ежемесячного аннуитетного платежа, содержат подробное описание хода решения. Учащиеся могут попробовать выполнить упражнение самостоятельно, после чего сравнить получившийся ответ с тем значением, которое представлено на сайте. Последовательно решая простые и более сложные задачи по данной теме, учащиеся смогут понять, как применяется формула аннуитетного платежа и как осуществляется ее вывод. Перечень заданий в соответствующем разделе постоянно дополняется и обновляется.

Попрактиковаться в решении задач, в которых применяется формула суммы аннуитетного платежа, можно в режиме онлайн. В случае необходимости любое из представленных упражнений можно сохранить в разделе «Избранное». В дальнейшем выпускник сможет вернуться к задаче с применением формулы ежемесячного аннуитетного платежа, для того чтобы обсудить алгоритм ее решения с преподавателем.

Источник

Формула и расчет аннуитетного платежа по кредиту

Итак, друзья, вот мы и добрались до самого интересного – до формул и расчетов, связанных с аннуитетными платежами. Хотя врём, данная тема скучна и неинтересна. Кто не «дружит» с математикой может сейчас начать зевать, а на определённом этапе – впасть в ступор.

Тем не менее, команда портала temabiz.com решила рискнуть и написать простыми словами о формулах и расчетах аннуитетных платежей. Что из этого получилось, вы узнаете, прочитав эту публикацию.

Формула расчета аннуитетных платежей

Вы точно уверены, что хотите увидеть формулу аннуитетного платежа? Хорошо, вот она:

P – ежемесячный платёж по аннуитетному кредиту (тот самый аннуитетный платёж, который не изменяется в течение всего периода погашения кредита);
S – сумма кредита;
i – ежемесячная процентная ставка (рассчитывается по следующей формуле: годовая процентная ставка/100/12);
n – срок, на который берётся кредит (указывается количество месяцев).

На первый взгляд данная формула может показаться страшной и непонятной. С другой стороны, а надо ли её понимать? Вам же требуется всего лишь рассчитать сумму аннуитетного платежа, верно? А что для этого надо? Правильно, надо просто подставить в формулу свои значения и произвести расчеты. Давайте сейчас этим и займёмся!

Расчёт аннуитетного платежа по кредиту

Допустим, вы решили взять в кредит 50 000 рублей на 12 месяцев под 22% годовых. Естественно, тип погашения будет аннуитетный. Вам надо рассчитать сумму ежемесячных взносов по кредиту.

Давайте для начала красиво оформим наши исходные данные (они нам понадобятся не только в этом, но и в дальнейших расчетах):

Сумма кредита: 50 000 руб.
Годовая процентная ставка: 22%.
Срок кредитования: 12 месяцев.

Итак, прежде чем приступить к расчёту аннуитетного платежа, надо посчитать ежемесячную процентную ставку (в формуле она скрывается под символом i и рассчитывается так: годовая процентная ставка/100/12). В нашем случае получится следующее:

Теперь, когда мы нашли значение i, можно приступать к расчёту размера аннуитетного платежа по нашему кредиту:

Путём несложных математических вычислений выяснилось, что сумма ежемесячных отчислений по нашему кредиту будет равна 4680 рублей.

В принципе, на этом можно было бы закончить нашу статью, но вы же наверняка хотите знать больше. Правда? Вот скажите, вы хотите знать, какую долю в данных выплатах составляют проценты по кредиту, а какую – тело кредита? Да и вообще, сколько вы переплатите по кредиту? Если да, тогда мы продолжаем!

График погашения кредита аннуитетными платежами

Вначале мы продемонстрируем вам сам график аннуитетных платежей, проанализируем его вместе с вами, а уж затем детально расскажем о том, как и по каким формулам мы его рассчитали.

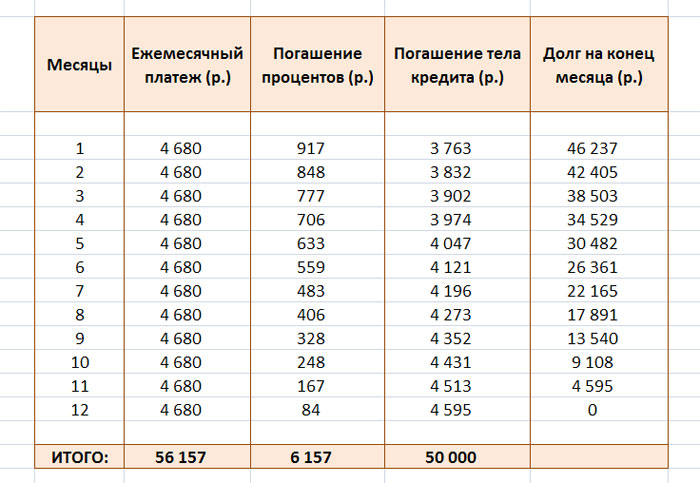
Вот так выглядит аннуитетный график погашения нашего кредита:

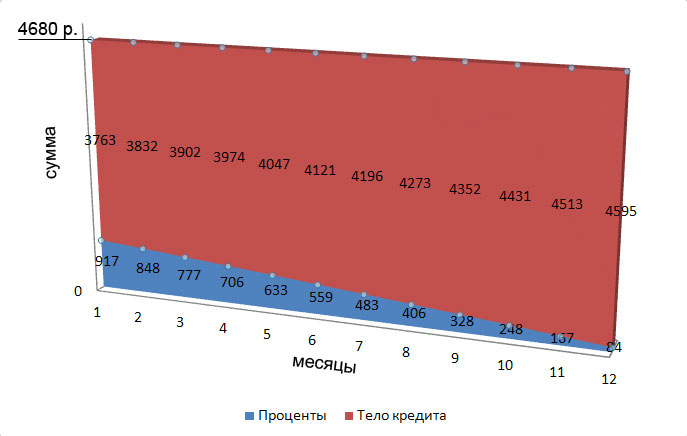
А это диаграмма (для наглядности):

И график, и диаграмма подтверждают написанное в публикации: Что такое аннуитетные платежи. Если вы по каким-то причинам её не читали, то обязательно это сделайте – не пожалеете. А те, кто читал, могут убедиться, что в аннуитетном графике погашения кредита выплаты осуществляются равными суммами, на начальном этапе доля процентов по кредиту самая высокая, а ближе к окончанию срока она существенно снижается.

Обратите внимание на то, что тело кредита погашается с первого же месяца кредитования. Просто на некоторых сайтах можно прочитать что-то типа такого: «При аннуитетной схеме погашения займа, вначале выплачиваются проценты, а уже потом само тело кредита». Как видите, это утверждение не соответствует действительности. Правильнее будет сказать так:

Аннуитетные платежи содержат в себе на начальном этапе высокую долю процентов по кредиту.

Тело же кредита тоже погашается с первого месяца кредитования. Тем самым, уменьшается сумма долга и, соответственно, размер выплат процентов по кредиту.

Теперь давайте детальнее изучим наш график аннуитетных платежей. Как видите, ежемесячный платёж у нас составляет 4680 рублей. Именно эту сумму мы будем каждый месяц выплачивать банку на протяжении всего срока кредитования (в нашем случае – на протяжении 12 месяцев). В результате, общая сумма выплат составит 56 157 рублей. В кредит же мы брали 50 000 рублей (в графике это четвёртая колонка, которая называется «Погашение тела кредита»). Получается, что переплата по данному займу составит 6157 рублей. Собственно, это и есть проценты по кредиту, которые указаны в третьей колонке нашего графика аннуитетных платежей. Получается, что эффективная процентная ставка (или полная стоимость кредита) у нас составит – 12,31%. Давайте «красиво» оформим данную информацию:

Ежемесячный аннуитетный платёж: 4680 руб.
Тело кредита: 50 000 руб.
Общая сумма выплат: 56 157 руб.
Переплата (проценты) по кредиту: 6157 руб.
Эффективная процентная ставка: 12,31%.

Итак, мы с вами проанализировали график аннуитетных платежей. Осталось понять, как вычисляется процентная доля и доля тела кредита в ежемесячных выплатах. Вот почему в первый месяц проценты составляют именно 917 рублей, во второй – 848 рублей, в третий – 777 рублей и т.д.? Хотите узнать? Тогда читайте дальше!

Расчёт процентов по аннуитетным платежам

Посчитать долю процентов в аннуитетных платежах вам поможет вот эта формула:

I_n – сумма в аннуитетном платеже, которая идёт на погашение процентов по кредиту;
S_n – сумма оставшейся задолженности по кредиту (остаток по кредиту);
i – уже знакомая вам ежемесячная процентная ставка (в нашем случае она равна – 0.018333).

Давайте для наглядности рассчитаем долю процентов в первом платеже по нашему кредиту:

Так как это первый платёж, то суммой оставшейся задолженности по кредиту является весь кредит – 50 000 руб. Умножив эту сумму на ежемесячную процентную ставку – 0.018333, мы и получим 917 руб. – сумму, указанную в нашем графике.

При расчёте суммы процентов в следующем аннуитетном платеже, на месячную процентную ставку умножается долг, который сформировался на конец предыдущего месяца (в нашем случае это 46 237 руб.). В результате получится 848 руб. – размер доли процентов во втором аннуитетном платеже. По такому же принципу рассчитываются проценты в остальных платежах. Далее давайте вычислим составляющую в аннуитетных платежах, которая пойдёт на погашение тела кредита.

Расчёт доли тела кредита в аннуитетных платежах

Зная долю процентов в аннуитетном платеже, можно легко посчитать долю тела кредита. Формула расчёта проста и понятна:

S – сумма в аннуитетном платеже, которая идёт на погашение тела кредита;
P – ежемесячный аннуитетный платёж;
I_n – сумма в аннуитетном платеже, которая идёт на погашение процентов по кредиту.

Как видите, здесь нет ничего сложного. По сути, аннуитетный платёж содержит в себе две составляющие:

Если нам известна величина самого аннуитетного платежа и размер процентной доли, то на погашение тела кредита в этом платеже пойдёт то, что останется после вычитания из него суммы процентов.

Расчёт доли тела кредита в нашем первом платеже выглядит так:

Надеемся, теперь всем понятно, откуда в графе «Погашение тела кредита» нашего графика аннуитетных платежей в выплатах за первый месяц взялась сумма 3763 руб. Да-да, это именно то, что осталось после того, как мы из суммы аннуитетного платежа (4680 руб.) вычли сумму процентов по кредиту (917 руб.). Аналогичным образом рассчитаны значения этой графы за последующие месяцы.

Итак, с телом кредита разобрались. Теперь осталось выяснить, как рассчитывается долг на конец месяца (в графике аннуитетных платежей это у нас последняя колонка).

Как рассчитать долг на конец месяца в графике аннуитетных платежей

Прежде всего, надо понимать, что именно является вашим долгом по кредиту, и какие выплаты способствуют его уменьшению. В нашем примере вы берёте в кредит 50 000 рублей – это и есть ваш долг. Переплаченные по кредиту проценты (6157 рублей) вашим долгом не являются, это всего лишь вознаграждение банку за предоставленный кредит. Таким образом, можно сделать вывод:

Погашение процентов по кредиту никак не способствует уменьшению вашего долга перед банком.

В кризисные времена банки часто «идут навстречу» своим должникам. Они говорят как-то так: «Мы понимаем, у вас сейчас проблемы! Окей, наш банк готов пойти вам на уступки – можете нам просто погашать проценты, а само тело кредита погашать не надо. Все же люди братья и должны друг другу помогать! Бла-бла-бла…»

На первый взгляд такое предложение может показаться выгодным, а сам банк – «белым и пушистым лапулей». Ага, как бы ни так! Если взять в руки калькулятор и провести простые арифметические расчёты, то сразу становится ясно, что реальное предложение банка выглядит приблизительно так:

«Ребята, вы попали на деньги! Ничего не поделаешь, это жизнь! Предлагаем вам на время (а может и навсегда) стать нашим рабом – будете ежемесячно выплачивать проценты по кредиту, а сам долг погашать не надо (ну, чтобы сумма выплат по процентам не уменьшалась). Ничего личного – это просто бизнес, друзья!»

Теперь запомните главную мысль:

Именно погашение тела кредита вытаскивает вас из долговой ямы. Не процентов, а именно тела кредита.

Наверняка вы уже догадались, как рассчитывается долг на конец месяца в нашем графике платежей. В общем, формула выглядит так:

S_n2 – долг на конец месяца по аннуитетному кредиту;
S_n1 – сумма текущей задолженности по кредиту;
S – сумма в аннуитетном платеже, которая идёт на погашение тела кредита.

Обратите внимание! При расчёте долга на конец месяца, от общей суммы текущей задолженности отнимается только та часть платежа, которая идёт на погашение тела кредита (уплаченные проценты сюда не входят).

Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

Итак, при первом платеже текущая задолженность по кредиту у нас равна всей сумме займа (50 000 руб.). Чтобы посчитать долг на конец месяца, мы отнимаем от этой суммы не весь ежемесячный платёж (4680 руб.), а только ту часть, которая ушла на погашение тела кредита (3763 руб.). В результате наш долг на конец месяца составит 46 237 руб., именно на эту сумму будут начисляться проценты в следующем месяце. Естественно, они будут меньше, так как сумма долга уменьшилась. Теперь вы понимаете, почему важно погашать именно тело кредита?

Итак, друзья, мы с вами разобрались с формулами и расчетами аннуитетных платежей. Надеемся, теперь у вас нет вопросов по этой теме, и вы запросто сможете произвести все необходимые расчеты, а также составить график аннуитетных платежей по кредиту. Единственное, что бы вам, наверное, хотелось, это как-то автоматизировать процесс расчетов. Вы не поверите, но это возможно! Хотите узнать как? Тогда переходим к публикации: Расчет аннуитетных платежей по кредиту в Excel.

Источник