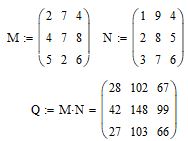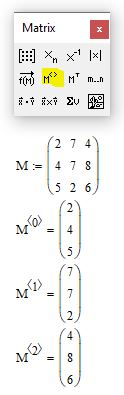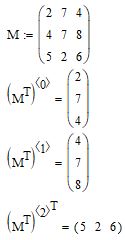Как вывести матрицу в маткаде
Урок 21. Векторы и матрицы в Mathcad
С этими понятиями Вы могли сталкиваться, работая в Excel – столбец чисел называется вектор-столбцом, строка – вектор-строкой. Блок объектов является матрицей. Вычисления в Excel, по сути, являются операциями с векторами и матрицами. В этом уроке мы познакомимся с аналогичными вычислениями в Mathcad, и мы поймем, почему в Mathcad их проводить проще.
Введение
В предыдущих уроках наши векторы начинались с элемента с номером «0». В этом уроке для простоты сделаем номер первого элемента равным «1». Это можно сделать с помощью вкладки Расчет –> Параметры документа –> ORIGIN:
Это значение можно вывести прямо в документ, чтобы не забыть его и не запутаться:
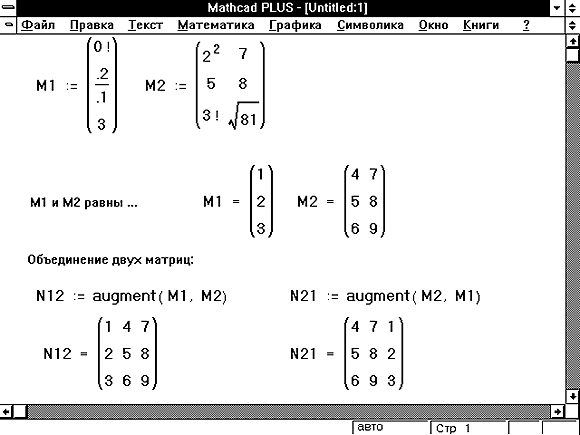
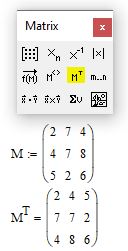
Теперь рассмотрим несколько матриц:
Как видно, они могут включать в себя числа, символы и даже функции. Они также могут содержать текстовые элементы (строки).
Элемент матрицы можно вывести, используя подстрочные индексы:
Матрицы выше являются квадратными 2х2, но у них может быть любой размер по строкам и столбцам:
Запомните: первое число – номер строки (или их количество), второе – столбца.
Элементы, выделенные с помощью подстрочных индексов:
Для вектор-столбца второй индекс можно опустить, но не для вектор-строки:
Во вкладке Математика –> Операторы и символы –> Операторы –> Векторы и матрицы Вы найдете команды для выделения столбцов и строк:
Многие операции для векторов и матриц аналогичны операциям для обычных чисел, переменных и функций: сложение, вычитание, некоторые виды умножения. Поиск обратной матрицы близко к операции деления. Вы можете записать эти операторы, используя имена векторов и матриц. В качестве примера рассмотрим векторное произведение матрицы и вектора:
Мы рассмотрим эту операцию подробнее позже. Однако стоит заметить, что она требует девять операций умножения и девять – сложения. Расписывать их утомительно и чревато ошибками – для больших матриц сделать это очень трудно.
Применение векторов очень широко. Вспомните пиксели на экране монитора – их могут быть миллионы. Они обрабатываются с помощью операций с матрицами.
В Mathcad
Для создания вектора или матрицы откройте вкладку Матрицы/таблицы. Когда курсор находится в пустой области щелкните по самой левой кнопке «Вставить матрицу». Появится сетка с маленькими квадратами:
Перемести указатель на сетку, выберите желаемый размер матрицы, затем щелкните левой кнопкой мыши. Появится пустая матрица:
Матрице можно присвоить имя, щелкнув на левую скобку, нажав [:] для оператора присваивания и введя имя:
Вставку и удаление строк и столбцов легко осуществлять с помощью команд из меню «Операторы с векторами/матрицами» на вкладке Матрицы и таблицы:
Операции с матрицами
Эффект от различных операций с матрицами и векторами будет проще понять, используя символы. Будем использовать две матрицы и два вектора:
Оператор транспонирования находится на вкладке Математика –> Операторы –> Векторы и матрицы:
Щелкните по правой границе матрицы и примените оператор. Он работает как для символьных, так и для числовых матриц:
Часто операции в векторами приходится совершать поэлементно. Для этого служит оператор векторизации. Операции в Excel зачастую являются поэлементными, они также важны и в Mathcad. Чтобы перемножить два вектора поэлементно, сначала введите простое умножение:
Затем выберите все выражение и примените векторизацию:
Вычислите, чтобы посмотреть результат: первый элемент умножается на первый, второй – на второй, и т.д.:
Другие поэлементные операции:
Поэлементные операции применимы только к массивам одного размера.
Сложение и вычитание
Сложение и вычитание выполняется поэлементно:
Эта операция также применима лишь к массивам одного размера.
С помощью оператора суммирования можно найти сумму всех элементов вектора (не матрицы):
Умножение на константу работает так:
При скалярном умножении матриц происходит умножение строк на столбцы. При этом используется тот же символ, что и при обычном умножении. Эта операция допустима только для тех матриц, в которых число строк в первой матрице равно числе столбцов во второй. Для наших матриц 2х2:
Заметьте, что последовательность множителей играет роль:
Скалярное произведение не коммутативно, за исключением особых случаев:
Скалярное произведение двух векторов дает результат с комплексно-сопряженными числами (с чертой сверху). Для действительных чисел на это можно не обращать внимания:
Этот оператор применим только для двух вектор-столбцов, состоящих из трех элементов:
Векторное произведение имеет широкое применение в механике, гидродинамике, электромагнетизме и в других областях.
Обратная матрица определяется только для квадратных матриц:
Произведение матрицы и ее обратной матрицы является единичной матрицей:
Произведение матрицы и единичной матрицы дает изначальную матрицу:
Определитель можно найти только для квадратной матрицы. Его значение может быть равно нулю, даже если все элементы матрицы не равны нулю. Обратная матрица содержит дроби, в знаменателе которых находится определитель:
Если определитель равен нулю, обратной матрицы не существует, а матрица является сингулярной. Вспомните деление на ноль в обычной алгебре. Mathcad сообщит, если матрица является сингулярной:
Для скаляра определитель равен его модулю:
Для вектора команда Определитель вычисляет длину вектора:
Резюме
В этом уроке мы рассмотрели векторы и матрицы (массивы).
Операции над векторами и матрицами, которые мы рассмотрели:
Как вывести матрицу в маткаде
После вычислений в Mathcad возникающие в результате массивы могут оказаться при отображении громоздкими и неуклюжими. Поэтому Mathcad отображает матрицы и векторы, имеющие более чем девять строк или столбцов, в виде таблиц вывода с полосами прокрутки, а не в виде матриц или векторов. Рисунок 7 показывает пример.
Рисунок 7: Отображение большого массива в виде таблицы вывода с полосами прокрутки.
Таблица вывода с полосами прокрутки отображает часть массива. Слева от каждой строки и наверху каждого столбца имеется число, указывающее индекс строки или столбца. Используйте эти заголовки строк и столбцов, чтобы определить индексы каждого значения в таблице.
Если элемент, который нужно увидеть, вне поля зрения, используйте полосу прокрутки для перемещения по таблице точно так же, как она используется для перемещения по любому другому окну.
В дополнение к возможности изменять размеры и пролистывать таблицу вывода можно копировать одно или несколько значений из таблицы и вставлять их в другую часть вашего рабочего документа либо в другую прикладную программу Windows.
Изменение способа отображения массивов
Графическое представление матриц
Многочисленные примеры трехмерных графиков матриц приводятся, начиная с Главы “Графики поверхностей”. Пример просмотра матрицы в полутоновых изображениях показан на последнем рисунке Главы “Программирование”.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Работа с матрицами в MathCad 15
В статье рассмотрены основные возможности mathcad 15 для работы с матрицами
Ввод матрицы
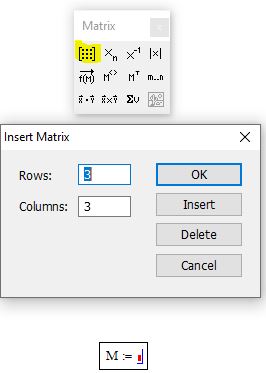
Чтобы ввести матрицу в mathcad 15 нужно в свободном поле ввести с клавиатуры имя матрицы. Пусть это будет M. Затем на панели Matrix нужно нажать кнопку «Matrix or vector». В появившемся окне нужно ввести количество строк и столбцов и нажать OK
Рис. 1. Ввод матрицы
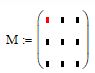
Затем появится заготовка матрицы с пустыми маркерами для ввода элементов вручную. См. рис. 2
Рис. 2. Заполнение матрицы
Перемножение матриц
Как известно, перемножение матриц осуществляется по правилу «строка на столбец». Введем 2 матрицы 3 х 3 с именами M и N. Перемножение матриц осуществляется с помощью стандартной операции умножения. На рис. 3 смотрите синтаксис записи
Рис. 3. Перемножение матриц
Транспонирование матриц
Как известно, при транспонировании матрицы ее строки становятся столбцами. В mathcad есть функция, которая позволяет выполнить транспонирование. Введите имя матрицы, которую хотите транспонировать, и на панели Matrix нажмите кнопку «Matrix transpose». На рис. 4 смотрите синтаксис для записи этой операции.
Рис. 4. Транспонирование матрицы
Обратные матрицы
Как известно, обратной матрицей M^-1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку «Invers». на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы
Рис. 5. Обратная матрица
Выделение столбца и строки из матрицы
Для того чтобы «вытащить» столбец из матрицы можно воспользоваться стандартной функцией mathcad из панели matrix. Введите произвольную матрицу M и затем ниже в рабочем поле mathcad выполните операцию, как показано на рис. 6. Обратите внимание, что по умолчанию номера столбцов и строк индексируются с «нуля»
Рис. 6. Выделение столбца матрицы
Аналогичным способом можно выделить строку, но для этого матрицу предварительно нужно транспонировать. При этом строка будет отображена в виде столбца. Если вы хотите получить результат в виде строки, то операцию транспонирования нужно провести 2 раза. Синтаксис будет выглядеть как на рисунке 7
Рис. 7. Выделение строки матрицы
Обратите внимание, что если при перемножении матриц их размерность «не совпадает» то mathcad выдаст ошибку
Обратите внимание, что обратная матрица не всегда может существовать для исходной матрицы
Donec eget ex magna. Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fergiat. Pellentesque in mi eu massa lacinia malesuada et a elit. Donec urna ex, lacinia in purus ac, pretium pulvinar mauris. Curabitur sapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Duis dapibus rutrum facilisis. Class aptent taciti sociosqu ad litora torquent per conubia nostra, per inceptos himenaeos. Etiam tristique libero eu nibh porttitor fermentum. Nullam venenatis erat id vehicula viverra. Nunc ultrices eros ut ultricies condimentum. Mauris risus lacus, blandit sit amet venenatis non, bibendum vitae dolor. Nunc lorem mauris, fringilla in aliquam at, euismod in lectus. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas. In non lorem sit amet elit placerat maximus. Pellentesque aliquam maximus risus, vel venenatis mauris vehicula hendrerit.
Interdum et malesuada fames ac ante ipsum primis in faucibus. Pellentesque venenatis dolor imperdiet dolor mattis sagittis. Praesent rutrum sem diam, vitae egestas enim auctor sit amet. Pellentesque leo mauris, consectetur id ipsum sit amet, fersapien risus, commodo eget turpis at, elementum convallis elit. Pellentesque enim turpis, hendrerit tristique lorem ipsum dolor.
Как вывести матрицу в маткаде
Векторы и матрицы рассматриваются в программе Mathcad как одномерные и двумерные массивы данных.
Матрица создается с помощью диалогового окна Вставить матрицу (рис. 1.6), которое открывают командой Вставка > Матрица (Insert > Matrix) или первой кнопкой на панели «Матрица» (рис. 1.7). Вектор задается как матрица, имеющая один столбец. В диалоговом окне задается число строк и столбцов, а после вставки на рабочий лист матрица содержит вместо элементов заполнители, вместо которых следует вставить число, переменную или выражение.
Для матриц определены сложение, умножение на число, перемножение и другие операции. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы:
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля, что задается системной переменной ORIGIN, и может быть изменено пользователем (например, блок ORIGIN:=1 устанавливает начальный индекс равным единице). Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Индекс (Subscript, xn) на панели инструментов Mатрица (Matrix) или нажатием символа «[» после имени массива (см. приложение «Горячие клавиши»). Индексы двумерных матриц записываются через запятую.
Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки: . Для его ввода используется кнопка Столбец (Matrix Column) на панели инструментов Матрица или соответствующая «горячая» клавиша.
На рис. 1.8 приведены примеры реализации некоторых операций с матрицами.
Векторы и матрицы в MathСad
Вы уже наверняка не раз сталкивались с такими понятиями как векторы и матрицы. Вектор – это обыкновенный столбец с числами. Матрица представляет собой сборный блок с объектами. Именно на работе с этими элементами построен принцип функционирования программы Excel. В этом уроке мы расскажем о том, как работать с такими вычислениями в программе Маткад и акцентируем внимание на том, почему процесс работы в данном ПО куда проще и удобнее.
Мы уже рассказывали в своих уроках о том, что все наши векторы начинались с элемента с нулевым значением. Сейчас же мы поставим номером первого элемента цифру один, ведь так нам гораздо проще будет сориентироваться в учебном материале.
Данное значение можно внести прямо в рабочее поле.
Посмотрите на матрицы на рисунке ниже.
Как вы можете заметить, в них входят и числа, и функции. Помимо этого, сюда можно внести и текст. Чтобы вывести элемент матрицы, воспользуйтесь подстрочным индексом.
Матрицы, описанные на скрине повыше, относятся к квадратному типу. Тем не менее, пользователь может самостоятельно устанавливать их размерные рамки.
Примите во внимание, что первое число обозначает общую нумерацию строчки, а второе – номер столбика.
Для векторного столбца второй индекс можно удалить. Для строки же он является обязательным.
Нужные команды, для всевозможного выделения строчек или столбиков вы всегда сможете отыскать во вкладке «Математика».
Большинство операций для векторных и матричных конструкций вполне соответствуют работе со стандартными числами и функциями. Для того, чтобы отыскать обратную матрицу, потребуется действовать по аналогии с операциями деления. Пользователь может записать операторы, задав им наименования матриц и векторов. Например, это может выглядеть так:
Более подробно мы рассмотрим данный опционал немного погодя. Стоит отметить, что такая функция нуждается в девяти операциях умножения и в таком же количестве деления. Согласитесь, что расписывать все эти процессы достаточно скучно. К тому же, с большими матрицами такой подход нерациональный.
Методика применения векторов отличается значительным разнообразием. Чтобы разработать вектор или матрицу, понадобится открыть вкладку «Вставить матрицу». На экране появится сетка с изображением маленьких квадратиков.
Перемещаем указатель на эту сетку. Настраиваем курсор на нужные габариты матрицы. Кликаем дважды ЛКМ.
На экране появляется новая матрица.
Матрица может быть переименована, после того, как пользователь дважды кликнет по левой скобке.
Чтобы быстро вставить или удалить строчки да столбцы, можно вызвать контекстное меню «Операторы с векторами\матрицами» на одноименной вкладке.
Работа с матрицами
Эффекты от матриц или вектором гораздо проще сообразить, пользуясь специально разработанными символами. Обратите внимание на скрин ниже.
Оператор транспортировки вызывается посредством выполнения операции Математика –> Операторы –> Векторы и матрицы:
Кликаем по правой стороне матрицы и применяем оператор. Он подходит как для символьных, так и численных матриц.
Операции в векторах часто выполняются по одному элементу. В этой ситуации можно воспользоваться очень удобным оператором, который отвечает за разработку вектора. Чтобы перемножить два вектора, понадобится выполнить простой пример.
Теперь нам нужно выбрать нужные параметры и активировать векторизацию.
Вычисляем заданные параметры и смотрим на результат. Первый элемент приумножился на второй, и так далее.
Еще примеры таких опций.
Операции поэлементного типа могут применяться исключительно к массивам одинакового размера.
Добавление и вычитание
Данные операции относятся к поэлементному типу.
Она также применяется к массивам одинакового размерного типа.
Пользуясь оператором, предназначенным для суммирования, можно отыскать сумму всех векторных частей.
Скалярное произведение работает по представленному ниже принципу.
При таком типе умножения матриц, программа занимается умножением данных элементов по столбцам. Данная операция может применяться исключительно к тем матрицам, которые характеризуются равным количеством строчек и столбцов.
Обратите внимание, что немалая роль отводится поочередности множителей.
Только в редких случаях скалярное произведение может стать коммутативным.
Скаляр двух векторов показывает результат как на фотографии ниже.
Данная опция может использоваться исключительно для двух векторных столбов из трех элементов.
Векторное произведение часто используется для механики, гидродинамики и огромного количества подобных сфер деятельности.
Обратная матрица может быть применима для квадратных матриц:
В результате у нас получится матрица единичного типа
Если произвести матрицу и единичную матрицу, мы получим первоначальный вариант.
Определитель может быть разработан исключительно для матрицы квадратного типа. Он может быть нулевым в любых условиях. Обратная матрица имеет в своей структуре дроби, в состав которых входит определитель.
В ситуациях, когда определитель установлен на ноль, к нему нереально подобрать обратную матрицу. Сама матрица автоматически становится сингулярной. О таких изменениях пользователь узнает из оповещения программы.
В ситуациях со скалярами, определитель соответствует их модулям
Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.
Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»
Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»
В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»
Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.
Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.
Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.