Как вывести погрешность косвенных измерений

Как вывести погрешность косвенных измерений

Погрешности прямых измерений. Промах. Систематическая погрешность. Случайная погрешность. Полная погрешность. Погрешности косвенных измерений. Запись результата измерений

Измерить физическую величину – это значит сравнить ее с однородной величиной, принятой за единицу меры.

Различают прямые и косвенные измерения.

Если измеряемая величина непосредственно сравнивается с мерой, то измерения называются прямыми. Например, измерения линейных размеров тел с помощью масштабной линейки и т.д.

Если измеряется не сама искомая величина, а некоторые другие величины, связанные с ней функциональной зависимостью, то измерения называются косвенными. Например, измерения объема, ускорения и т.д.

Из-за несовершенства средств и методик измерения, органов чувств при любом измерении неизбежны отклонения результатов измерений от истинных величин. Эти отклонения называются погрешностями измерений.

Погрешности измерений делятся на систематические, случайные и промахи.

1.1. Промахи, связанные с неправильными отсчетами по прибору, неправильными записями и т.д., приводят к очень большой по абсолютной величине погрешности. Они, как правило, не укладываются в общую закономерность измеренных величин. Обнаруженный промах следует отбросить.

1.2. Систематическими погрешностями Δx_сист называются погрешности, которые сохраняются при повторных измерениях одной и той же величины x или изменяются по определенному закону.

Систематические погрешности подразделяются на несколько групп. Отметим только приборную погрешность.

Систематическая приборная погрешность определяется по классу точности прибора, который указывается на приборе следующими цифрами: 0,01; 0,02; 0,05; 1,0; 2,5; 4,0. Класс точности показывает предельно допустимое значение систематической погрешности, выраженной в процентах от верхнего предела на выбранном диапазоне измерений. Например, предел измерения вольтметра с классом точности 0,5 равен 200 В. Систематическая погрешность равна 0,5% от 200В. Следовательно, систематическая погрешность вольтметра равна 1 В.

Если на приборе класс точности не указан, то погрешность равна половине цены наименьшего деления шкалы прибора.

1.3. Случайными называются погрешности, которые изменяются беспорядочно при повторных измерениях одной и той же физической величины при одинаковых условиях.

Оценим случайную погрешность. Пусть при измерении какой-либо физической величины было произведено N измерений и были получены значения x₁, x₂, … x_N. Тогда наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение

Результаты измерений x₁, x₂, … x_N «рассеиваются» вокруг среднего. В качестве меры «рассеяния» результатов наблюдения вокруг среднего служит среднее квадратичное отклонение

Пусть a будет истинным, но неизвестным значением измеряемой величины x. Доказано, что вероятность попадания результатов измерения величины x в интервал значений от (a – S) до (a + S) оказывается равной α = 0,68.

Вероятность попадания результатов наблюдений в более широкие интервалы (a – 2S, a + 2S) и (a – 3S, a + 3S) равна α = 0,95 и α = 0,99 соответственно.

Вероятность попадания в заданный интервал значений величины x называется доверительной вероятностью, а сам интервал – доверительным интервалом.

Однако, таким образом полученный доверительный интервал справедлив при большом значении N. В учебных лабораториях, как правило, приходится ограничиваться небольшим числом измерений. В этом случае доверительный интервал находят с помощью коэффициента Стьюдента, который зависит от числа измерений N и доверительной вероятности α. В таблице 1 приведены коэффициенты Стьюдента для различного числа наблюдений при доверительных вероятностях α = 0,68; 0,95; 0,99.

Источник

Нахождение погрешностей косвенных измерений

Нахождение погрешностей косвенных измерений

Косвенное измерение это определение искомого значения физической величины на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной.

Пример – Определение плотности D тела цилиндрической формы по результатам прямых измерений массой m, высотой hи диаметром цилиндра d, связанных с плотностью уравнением

П р и м е ч а н и е. Во многих случаях вместо термина «косвенное измерение» применяют термин «косвенный метод измерений».

Для вычисления погрешностей косвенных измерений по известным погрешностям прямых измерений существуют следующие методики.

Получение формул для вычисления погрешностей косвенных измерений в случае зависимости вида Y= a+b-c(сумма, разность).

Исходные данные: a=90, b=60, c=45, Дa=1, Дb=3, Дc=0,5.

Вывод формул для вычисления погрешностей косвенных измерений в рассматриваемом случае можно выполнить следующим образом.

Найдём дифференциал правой и левой частей:

dY= d(a +b-c) = da+ db-dc. (2)

2Произведём широко используемую в теории погрешностей замену
дифференциалов абсолютными погрешностями (при условии, что абсолютные погрешности достаточно малы): dY≈ ДY, da≈ Дa, db≈ Дb, dc≈ Дc. Тогда

3 Учитывая, что знаки погрешностей Дa, Дb, Дc обычно бывают заранее неизвестны, для получения гарантированной (предельной) оценки абсолютной погрешности косвенного измерения в последней формуле все знаки «–» заменим на знаки «+»:

4Найдём предельную оценку относительной погрешности косвенного измерения, учитывая, что относительная погрешность есть отношение абсолютной погрешности к результату измерений:

дYпр = ДY/Y = (Дa+Дb+Дc)/ (a+b-c) (6)

Величина предельной погрешности во многих случаях бывает завышенной, поэтому часто применяют среднеквадратические оценки погрешности. Для получения среднеквадратической оценки погрешности в формуле для предельной оценки погрешности сумму заменяют корнем квадратным из суммы квадратов.

5Найдём среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения:

(7)

(8)

Получение формул для вычисления погрешностей косвенныхизмерений в случае зависимости вида Y = a·b/с (произведение, деление).

Исходные данные: a, b, c, Дa, Дb, Дc. Вывод формул для вычисления погрешностей косвенных измерений в рассматриваемом случае можно выполнить следующим образом.

1Прологарифмируем левую и правую части заданной зависимости:

lnY = ln(ab/с) = lna + lnb–lnc (9)

2Найдём дифференциал правой и левой частей:

dlnY = dln(ab/с) =dlna + dlnb-dlnc (10)

3 Учитывая, что дифференциал от логарифма переменной величинынаходится по формулеd(lnx) = dln (x /dx )dx = dx/x, получаем:

dY/Y = da/a + db/b+dc/c (11)

4Произведём широко используемую в теории погрешностей заменудифференциалов малыми абсолютными погрешностями (при условии, чтоабсолютные погрешности достаточно малы):

dY ≈ДY, da≈Дa, db ≈Дb, dc ≈Дc, тогда

ДY/Y =Дa/a + Дb/b – Дc/c (12)

5 Учитывая, что знаки погрешностейДa, Д b, Дc заранее неизвестны, для получения гарантированной (предельной) оценки относительнойпогрешности косвенного измерения в последней формуле все знаки «-»заменяем на знаки «+»:

ДYпр/Y =Дa/a + Дb/b + Дc/c (13)

6 Предельную оценку абсолютной погрешности косвенного измерения находим по формуле:

Величина предельной погрешности во многих случаях бывает завышенной, поэтому часто применяют среднеквадратические оценки погрешности. Для получения среднеквадратической оценки погрешности в формуле для предельной оценки погрешности сумму заменяют корнем квадратным из суммы квадратов.

7Найдём среднеквадратические оценки относительной и абсолютной погрешностей косвенного измерения:

(15)

(16)

Пример решения задачи

По известной расчётной зависимости косвенного метода измерения и по известным результатам и погрешностям прямых измеренийрассчитать предельные и среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения.

a=50; Дa=1; b=90; Дb=3; c=60; Дc=2; d=70; Дd=2; e=40; Дe=1;

1 Подставив в выражение 17 соответствующие исходные данные получим:

Y = 2·(50+90)·602/(70-40) = 33600

2Введём обозначение ab =a+b, de =d-e, тогда:

3Прологарифмируем левую и правую части заданной зависимости 18:

4Найдём дифференциал правой и левой частей выражения 19:

dlnY = dln2+dlnab+2d lnc-dlnde (20)

С учётом того, что dln2 = 0, получим:

dlnY = dln ab+2dlnc-dlnde.

5 Учитывая, что дифференциал от логарифма переменной величины находится по формуле d(lnx) = dln (x /dx )dx = dx/x, получаем:

6 Произведём широко используемую в теории погрешностей замену дифференциалов малыми абсолютными погрешностями (при условии, что абсолютные погрешности достаточно малы), т. е.:

dY ≈ ДY, dab ≈ Дab, dc ≈ Дc, dde ≈ Дde, тогда

ДY/Y =Дab/ab + 2Дc/c – Дde/de (22)

7 Учитывая, что знаки погрешностей Дab, Дc, Дde заранее неизвестны, для получения гарантированной (предельной) оценки относительной погрешности косвенного измерения Y в последней формуле все знаки «-» заменяем на знаки «+».

По формуле 13 получим предельную оценку относительной погрешности косвенного измерения:

ДYпр/Y = Дab/ab + 2Дc/c + Дde/de (23)

Здесь ab = a + b, тогда Дab= Дa+ Дb, de = d–e, окончательно получим:

ДYпр/Y = (Дa + Дb)/(a +b) + 2Дc/c + (Дd + Дe) /(d-e) (24)

Подставляя значения в выражение 24и учитывая, что a+b = 140, а d – e = 30, получим:

ДYпр/Y =(1+3) /140+ 2*2/60 + (2 +1)/30 = 0.1952

8 Предельную оценку абсолютной погрешности косвенного измерения находим по формуле 14:

Подставляя значения и с учетом того, что Y = 33600, получим:

дYпр = 0.1952·33600 = 6558.7

В % погрешность составит 19.52

9Найдём среднеквадратические оценки относительной и абсолютной погрешностей косвенного измерения Y с учётом того, чтовместо квадрата abнужно подставлять:

Аналогично вместо квадрата de

По формуле 15 получим:

дYск = (ДY/Yск)·Y = 0.0910·33600 = 3057

В % погрешность составит 9.1

По известной расчётной зависимости косвенного метода измерения и по известным результатам и погрешностям прямых измерений, в соответствии с полученным вариантом, рассчитать предельные и среднеквадратические оценки абсолютной и относительной погрешностей косвенного измерения. Исходные данные приведены в таблице 1.

Источник

Как вывести погрешность косвенных измерений

В лабораторной практике большинство измерений – косвенные и интересующая нас величина является функцией одной или нескольких непосредственно измеряемых величин:

Как следует из теории вероятностей, среднее значение величины определяется подстановкой в формулу (13) средних значений непосредственно измеряемых величин, т.е.

Требуется найти абсолютную и относительную ошибки этой функции, если известны ошибки независимых переменных.

Рассмотрим два крайних случая, когда ошибки являются либо систематическими, либо случайными. Единого мнения относительно вычисления систематической ошибки косвенных измерений нет. Однако, если исходить из определения систематической ошибки как максимально возможной ошибки, то целесообразно находить систематическую ошибку по формулам

Формулой (15) удобно пользоваться в случае, если функция имеет вид суммы или разности аргументов. Выражение (16) применять целесообразно, если функция имеет вид произведения или частного аргументов.

Для нахождения случайной ошибки косвенных измерений следует пользоваться формулами:

В этом случае надежность для доверительного интервала ΔN будет тоже P.

Часто наблюдается случай, когда систематическая ошибка и случайная ошибка близки друг к другу, и они обе в одинаковой степени определяют точность результата. В этом случае общая ошибка ∑ находится как квадратичная сумма случайной Δ и систематической δ ошибок с вероятностью не менее чем P, где P – доверительная вероятность случайной ошибки:

При проведении косвенных измерений в невоспроизводимых условиях функцию находят для каждого отдельного измерения, а доверительный интервал вычисляют для получения значений искомой величины по тому же методу, что и для прямых измерений.

Следует отметить, что в случае функциональной зависимости, выраженной формулой, удобной для логарифмирования, проще сначала определить относительную погрешность, а затем из выражения ΔN = ε ¯ N найти абсолютную погрешность.

Прежде чем приступать к измерениям, всегда нужно подумать о последующих расчетах и выписать формулы, по которым будут рассчитываться погрешности. Эти формулы позволят понять, какие измерения следует производить особенно тщательно, а на какие не нужно тратить больших усилий.

При обработке результатов косвенных измерений предлагается следующий порядок операций:

Приведем примеры расчета ошибки косвенного измерения.

Пример 1.Находится объем цилиндра по формуле

где d – диаметр цилиндра, h – высота цилиндра.

Обе эти величины определяются непосредственно. Пусть измерение этих величин дало следующие результаты:

h = (8.65 ± 0.02) мм, при одинаковой надежности Р = 0.95.

Среднее значение объема, согласно (14) равно

Воспользовавшись выражением (18) имеем:

Систематическая ошибка оказывается сравнимой со случайной, следовательно

Таким образом, результат измерения оказывается

Пример 2. Найти абсолютную и относительную погрешности для следующей функциональной зависимости:

В этом случае удобнее сначала искать относительную погрешность. Тогда

Используя формулу (18), получим

Абсолютную случайную погрешность найдем из выражения

Используя формулу (16) получаем

Абсолютную систематическую ошибку найдем из выражения

Приведем таблицу расчета систематических погрешностей для простейших функций.

Таблица расчета случайных погрешностей для простейших функций.

Источник

Расчет погрешностей при косвенных измерениях

В большинстве случаев конечной целью лабораторной работы является вычисление искомой величины с помощью некоторой формулы, в которую входят величины, измеряемые прямым путем. Такие измерения называются косвенными. В качестве примера приведем формулу плотности твердого тела цилиндрической формы

, (П.5)

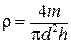
Зависимость (П.5) в общем виде можно представить следующим образом:

, (П.6)

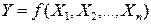
При расчете погрешностей в случае косвенных измерений удобно придерживаться такой последовательности действий:

1) получить средние значения каждой прямо измеряемой величины áX₁ñ, áX₂ñ, …, áX_nñ;

2) получить среднее значение косвенно измеряемой величины áYñ, подставив в формулу (П.6) средние значения прямо измеряемых величин;

4) основываясь на явном виде функции (П.6), получить формулу для расчета абсолютной погрешности косвенно измеряемой величины DY и рассчитать ее;

5) рассчитать относительную погрешность измерения ;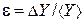

6) записать результат измерения с учетом погрешности.

Ниже без вывода приводится формула, позволяющая получить формулы для расчета абсолютной погрешности, если известен явный вид функции (П.6):

, (П.7)

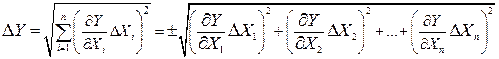
где ¶Y¤¶X₁ и т. д. – частные производные от Y по всем прямо измеряемым величинам X₁, X₂, …, X_n (когда берется частная производная, например по X₁, то все остальные величины X_i в формуле считаются постоянными), DX_i– абсолютные погрешности прямо измеряемых величин, вычисленные согласно (П.3).

Рассчитав DY, находят относительную погрешность .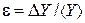

Однако если функция (П.6) является одночленом, то намного легче сначала рассчитать относительную погрешность, а затем уже абсолютную.

Действительно, разделив обе части равенства (П.7) на Y, получим

.

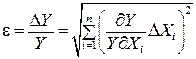
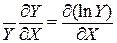
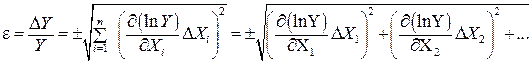
Но так как , то можно записать

. (П.8)

Теперь, зная относительную погрешность, определяют абсолютную .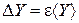

В качестве примера получим формулу для расчета погрешности плотности вещества, определяемой по формуле (П.5). Поскольку (П.5) является одночленом, то, как сказано выше, проще сначала рассчитать относительную погрешность измерения по (П.8). В (П.8) под корнем имеем сумму квадратов частных производных от логарифма измеряемой величины, поэтому сначала найдем натуральный логарифм r:

ln r = ln 4 + ln m – ln p –2 ln d – ln h,

а потом уже воспользуемся формулой (П.8) и получим, что

. (П.9)

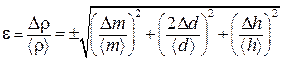
Как видно, в (П.9) используются средние значения прямо измеряемых величин и их абсолютные погрешности, рассчитанные методом прямых измерений по (П.3). Погрешность, вносимую числом p, не учитывают, поскольку ее значение всегда можно взять с точностью, превышающей точность измерения всех других величин. Рассчитав e, находим .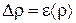

Если косвенные измерения являются независимыми (условия каждого последующего эксперимента отличаются от условий предыдущего), то значения величины Y вычисляются для каждого отдельного эксперимента. Произведя n опытов, получают n значений Y_i. Далее, принимая каждое из значений Y_i (где i – номер опыта) за результат прямого измерения, вычисляют áYñ и DY по формулам (П.1) и (П.2) соответственно.

Окончательный результат как прямых, так и косвенных измерений должен выглядеть так:

, (П.10)

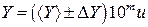
где m – показатель степени, u – единицы измерения величины Y.

Источник

Как вывести погрешность косвенных измерений

Чтобы найти погрешность косвенных измерений, надо воспользоваться формулами, приведенными в таблице. Эти формулы могут быть выведены «методом границ».

Сначала надо вспомнить основные понятия теории погрешности.

Так как мы никогда не знаем точного значения величины А, а лишь определяем из опыта ее приближенное значение, то и величину абсолютной погрешности мы можем определить лишь при­бли­зи­тель­но. Наиболее просто находится максимальная величина абсолютной погрешности, которая и используется нами в лабораторных работах.

Относительная погрешность измерения ε_А равна:

При косвенных измерениях величину погрешности искомой величины вычисляют по формулам:

В случае, когда искомая величина находится по формуле, в которой в основном присутствуют произведение и частное, удобней находить сначала относительную погрешность. Если при этом один из множителей представляет собой сумму или разность, нужно предварительно найти его абсолютную погрешность (сложением абсолютных погрешностей слагаемых), а затем относительную.

Зная относительную погрешность, найти абсолютную погрешность измерений можно так:

«Правило ничтожных погрешностей»

при суммировании погрешностей любым из слагаемых можно пренебречь, если оно не превосходит ⅓ – ⅟ 4 от другого.

Запись результата с указанием погрешности.

Абсолютная погрешность измерений обычно округляется до 1 значащей цифры, а, если эта цифра 1, то до двух.

Результат записывается в виде:

А = А_изм ± ΔА, например: ℓ = (13 ± 2) мм.

Пример оценки погрешностей косвенных измерений № 1

Пример оценки погрешностей косвенных измерений № 2

Задания для самостоятельного решения

Задание 1. Найдите плотность вещества, из которого сделан куб со стороной 7,00 ± 0,15 см, если его масса 847 ± 2 г. Что это за вещество?

Задание 2. Найдите удельную теплоту сгорания топлива, 2,10 ± 0,15 г которого хватило, чтобы нагреть 400 ± 10 мл воды на 35°С ± 2°С. Что это за топливо?

© Ивашкина Д.А., 2017. Публикация материалов с сайта разрешена только при наличии активной ссылки на главную страницу.

Источник