код хэмминга 7 4 пример для чайников
Код хэмминга 7 4 пример для чайников
Код Хэ́мминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построен применительно к двоичной системе счисления. Позволяет исправлять одиночную ошибку (ошибка в одном бите) и находить двойную.
Предположим, что нужно сгенерировать код Хемминга для некоторого информационного кодового слова. В качестве примера возьмём 15-битовое кодовое слово x1…x15, хотя алгоритм пригоден для кодовых слов любой длины. В приведённой ниже таблице в первой строке даны номера позиций в кодовом слове, во второй — условное обозначение битов, в третьей — значения битов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Вставим в информационное слово контрольные биты r0…r4 таким образом, чтобы номера их позиций представляли собой целые степени двойки: 1, 2, 4, 8, 16… Получим 20-разрядное слово с 15 информационными и 5 контрольными битами. Первоначально контрольные биты устанавливаем равными нулю. На рисунке контрольные биты выделены розовым цветом.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
В общем случае количество контрольных бит в кодовом слове равно двоичному логарифму числа, на единицу большего, чем количество бит кодового слова (включая контрольные биты); логарифм округляется в большую сторону. Например, информационное слово длиной 1 бит требует двух контрольных разрядов, 2-, 3- или 4-битовое информационное слово — трёх, 5…11-битовое — четырёх, 12…26-битовое — пяти и т. д.
Добавим к таблице 5 строк (по количеству контрольных битов), в которые поместим матрицу преобразования. Каждая строка будет соответствовать одному контрольному биту (нулевой контрольный бит — верхняя строка, четвёртый — нижняя), каждый столбец — одному биту кодируемого слова. В каждом столбце матрицы преобразования поместим двоичный номер этого столбца, причём порядок следования битов будет обратный — младший бит расположим в верхней строке, старший — в нижней. Например, в третьем столбце матрицы будут стоять числа 11000, что соответствует двоичной записи числа три: 00011.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | |||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
В правой части таблицы мы оставили пустым один столбец, в который поместим результаты вычислений контрольных битов. Вычисление контрольных битов производим следующим образом. Берём одну из строк матрицы преобразования (например, r0) и находим её скалярное произведение с кодовым словом, то есть перемножаем соответствующие биты обеих строк и находим сумму произведений. Если сумма получилась больше единицы, находим остаток от его деления на 2. Иными словами, мы подсчитываем сколько раз в кодовом слове и соответствующей строке матрицы в одинаковых позициях стоят единицы и берём это число по модулю 2.
Если описывать этот процесс в терминах матричной алгебры, то операция представляет собой перемножение матрицы преобразования на матрицу-столбец кодового слова, в результате чего получается матрица-столбец контрольных разрядов, которые нужно взять по модулю 2.
Например, для строки r0:
r0 = (1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·1+0·1+1·1+0·0+1·0+0·0+1·0+0·1) mod 2 = 5 mod 2 = 1.
Полученные контрольные биты вставляем в кодовое слово вместо стоявших там ранее нулей. По аналогии находим проверочные биты в остальных строках. Кодирование по Хэммингу завершено. Полученное кодовое слово — 11110010001011110001.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 | x14 | x15 | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
Алгоритм декодирования по Хэммингу абсолютно идентичен алгоритму кодирования. Матрица преобразования соответствующей размерности умножается на матрицу-столбец кодового слова и каждый элемент полученной матрицы-столбца берётся по модулю 2. Полученная матрица-столбец получила название «матрица синдромов». Легко проверить, что кодовое слово, сформированное в соответствии с алгоритмом, описанным в предыдущем разделе, всегда даёт нулевую матрицу синдромов.
Матрица синдромов становится ненулевой, если в результате ошибки (например, при передаче слова по линии связи с шумами) один из битов исходного слова изменил своё значение. Предположим для примера, что в кодовом слове, полученном в предыдущем разделе, шестой бит изменил своё значение с нуля на единицу (на рисунке обозначено красным цветом). Тогда получим следующую матрицу синдромов.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r0 | r1 | x1 | r2 | x2 | x3 | x4 | r3 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | r4 | x12 | x13 | x14 | x15 | ||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | ||
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | s0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | s1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | s2 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | s3 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | s4 | 0 |
Заметим, что при однократной ошибке матрица синдромов всегда представляет собой двоичную запись (младший разряд в верхней строке) номера позиции, в которой произошла ошибка. В приведённом примере матрица синдромов (01100) соответствует двоичному числу 00110 или десятичному 6, откуда следует, что ошибка произошла в шестом бите.
Код Хэмминга. Пример работы алгоритма
Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:
Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.
Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.
Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.
Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.
Как это работает.
Для того, чтобы понять работу данного алгоритма, рассмотрим пример.
Подготовка
Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):
Было:
Стало:
Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».
Вычисление контрольных бит.
Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее: 
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.
Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее: 
и для второй части:
Вот и всё! Первая часть алгоритма завершена.
Декодирование и исправление ошибок.
Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно): 
Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину: 
Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.
Заключение.
В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.
Примечание.
На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.
Код Хэмминга (7; 4)
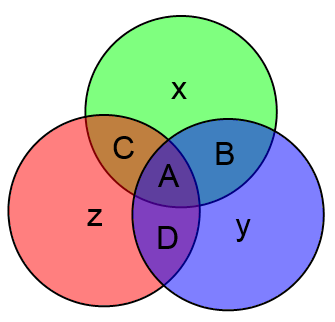
Структурно слова кода Хэмминга состоят из двух частей. Сначала идут информационные 4 бита, затем три бита проверочных. Будем обозначать информационные биты буквами ABCD, проверочные буквами xyz.
Таким образом слово кода Хэмминга имеет следующую структуру:
Для передачи 4 бит информации нам требуется передавать кодовое слово из целых 7 бит! Последние три бита в случае, когда ошибки отсутствуют, не несут никакой новой информации, ибо они зависят от первых 4. Однако если в кодовом слове из 7 бит произошла 1 ошибка, то исходные информационные 4 бита всё равно можно будет восстановить точно! В этом и состоит главная особенность самокорректирующихся кодов.
Для подсчёта проверочных бит можно использовать следующие формулы:
где n mod 2 означает остаток от деления числа n на 2.
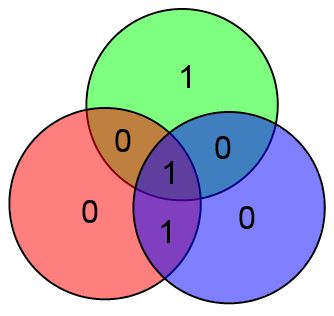
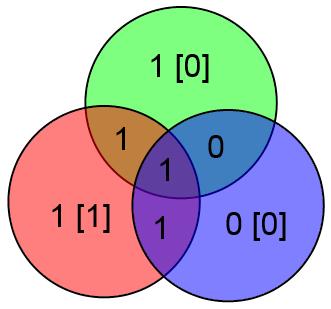
К примеру, если информационный вектор есть ABCD = 1001, то кодовый вектор будет ABCDxyz = 1001 100
Вместо непонятных формул можно использовать следующую картинку:
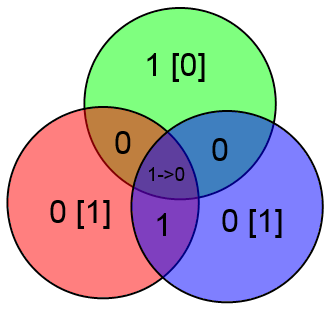
Здесь всё очень просто. Подставляете вместо букв значения соответствующих битов и затем считаете значения x, y и z как сумму по модулю 2 тех информационных бит, которые есть в соответствующем круге.
В приведённом выше примере будет:
Куда более интересным является вопрос об исправлении ошибок. Очевидно, вывод об отсутствии ошибок приёмник может сделать просто взяв информационные биты ABCD, посчитав на их основе проверочные биты xyz и сравнить посчитанные проверочные биты с принятыми. Если есть ошибка, то часть проверочных битов не совпадёт.
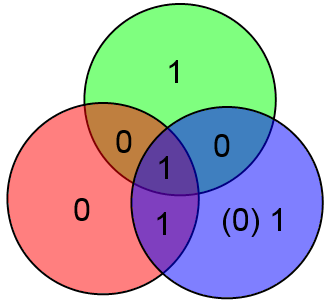
Предположим что произошла ошибка в проверочном бите y и было принято слово 1001 110
В таком случае два проверочных бита сойдутся, а один нет. Этого вполне достаточно чтобы сделать вывод что нужно исправить бит y (для которого проверка не сошлась).
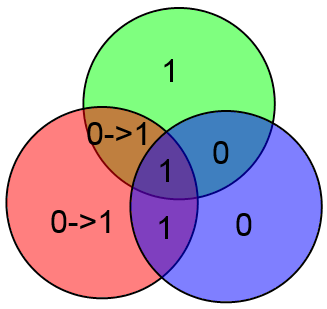
Наконец, отдельно рассмотрим бит A. Если в нём ошибка, то у нас не сойдутся все три проверки:
Увидев такое безобразие сразу же делаем вывод о том, что ошибка в бите A.
Таким образом, можно легко и просто вычислять локацию ошибки и исправлять её. Замечу что если ошибок больше одной, то описанный выше алгоритм сработает неверно. К примеру, допустим что произошли ошибки в битах C и z:
Проверочные биты y и z сойдутся, а бит x нет. Алгоритм исправит бит x и всё. Это вполне естественное поведение, т.к. если вероятность ошибки p 0).
Естественно, работать с цветными кругами удобно человеку, но неудобно компьютеру. У кодов Хэмминга есть одна особенность, которая позволяет их лёгкое декодирование на компьютере. Итак, рассмотрим следующий алгоритм:
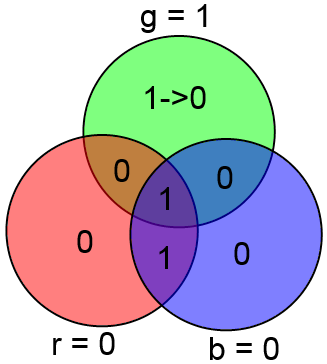
Определим числа g, b, r как сумму всех четырёх бит в кругах соответствующего цвета. Т.е.:
g = A + B + C + x mod 2,
b = A + B + D + y mod 2,
r = A + C + D + z mod 2.
Фактически каждый из этих бит можно определить как сумму соответствующего проверочного бита, вычисленного на основании принятых информационных бит, с принятым проверочным битом. Т.е. к примеру g есть сумма (A + B + C mod 2) (по этой формуле считался x на стороне передатчика) и принятого x. Аналогично b соответствует y, r соответствует z.
Если ошибок нет, то gbr = 000 (принятые проверочные биты сошлись с вычисленными на основе информационного вектора).
Если же есть 1 ошибка, то число gbr есть номер (в двоичной записи) ошибочного бита в векторе ABCxDyz.
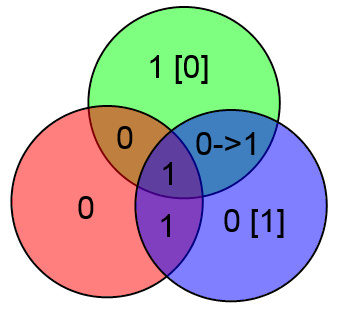
В качестве примера рассмотрим уже знакомый нам вектор ABCDxyz = 1001 100, в котором произошла ошибка в бите x (четвёртый бит в векторе ABCxDyz). Посчитаем gbr:
gbr = 100 [2] = 4 [10]. Ошибка в 4 бите, которым и является x. Таким образом, для декодирования и исправления ошибки в кодовом слове длины 7 требуется лишь вычислить три суммы и из полученного числа несложной функцией получить местонахождение ошибки.
На этом всё, спасибо за внимание!
Найдены возможные дубликаты
Сижу, раскуриваю коды Гоппы, и понимаю, какой милый и хороший был хэмминг 🙂
Спасибо огромное! Жаль нельзя поставить плюс(
спасибо, милый человек. благодаря посту лабу сделали xD
Нахрена мне знать об этом? т.е. какой профит? где оно надо?
Не нравится не читай. А мне было полезно.
Запоздалое спасибо. Пикабу образовательный 🙂
мне было интересно, но что дальше?
Да разве всё упомнишь
Игрушка
Я не видела его 20 лет. Конечно не узнала. Обнимаю. И спрашиваю:
— Как там поживает моя собака?
Прививки
Реклама
Регулярно вижу в ленте рекламу. Очень хочется её комментировать. Будет ли такая возможность когда либо? Я уверен что не один хочу этого.
Собеседование
Начальник цеха сегодня после совещания рассказывает:
Неудобно получилось
Не happy end
xxx: Что говорит «Найти телефон?» Я так свой нашел.
Было замечательно, телефон потерял и видел по ноутбуку, как он движется по карте.
Оказалось, что жена взяла вместе со своим по запарке и поехала к любовнику.
Вот так я нашел свой телефон.
yyy: История со счастливым концом.
Быдло напало на девочек
Вчера 03.10.2021 примерно в 16:50 этот биомусор напал на 2-х абсолютно невинных девочек, которые возвращались домой с прогулки. Девочка в розовой курточке, это дочка моей знакомой. Девочкам по 11 лет.
На видео слышно, как он им угрожает, пытается подпалить зажигалкой и наносит несколько ударов по голове обеим девочкам, после чего скрывается.
У обоих девочек остались следы от ударов, для детей его удары оказались достаточно сильные.
Как выяснилось позже, данный индивид вышел на улицу разбираться с обидчицами его собственной дочери, но так как он не знал как они выглядят, то напал на первых попавшихся ни в чём не повинных детей.
Ещё более мерзко то, что его дочь является их одноклассницей и девочки всегда с ним здоровались, но это ни как не остановило его.
В данный момент написано заявление у инспектора по делам несовершеннолетних, планируется так же написать заявление в МВД по факту нападения на детей.
П.С. Этот человек ранее уже был судим за убийство, у него четверо детей, живёт он в соседнем подъезде и о камере в домофоне прекрасно знает.
Неожиданно
Если это было на самом деле, то даме все равно грозит уголовка, так как она брала деньги за бесплатную процедуру.
Традиции
Pro свадьбу
Прочитал пост про свадьбу и комменты, про конкурсы, про тамадов, про чудных гостей.
Я вот на свадьбах редко бывал, ну так особо не приглашали почему-то, может город маленький, может кто оклеветал. На одной правда был, запомнилось.
Приехал я сразу в кафе, чего я в том Загсе не видел, ну расселись все, подарки, тосты, поздравления и вот такой тамундак и вёл, а давайте за молодых, за гостей, за гусей, за Варлей, музей и прочее прочее, все филонили кто как мог, кто воду пил, кто сок, а я честно в силу неопытности пил за все подряд, даже если тоста ещё небыло.
В определённый момент наступил апогей апофеоза, мне стало скучно, все пустились в пляс, плясать я не умею и я пошёл на улицу, а там фонтан, нет в ВДВ я не служил, даже в ВМФ не служил, но мне захотелось в водичку. Я человек крайне воспитанный и культурный взял стул с веранды, стол, затащил это все в фонтан пока все плясали я сварганил себе закуски, выпивки и сидел интилегентно выпивал и закусывал. Меня искали, меня нашли. Вся свадьба во главе с новобрачными водили хороводы вокруг фонтана умоляя меня вернуться на берег, я был категорически против, все ржали, жена плакала, оператор снимал на видео. Потом мне стало жаль жену, я её любил и я вернулся в зал к людям. Там были конкурсы, я захотел в них быть и на каждый вопрос «кто?» я с готовностью говорил» Я». Конкурсы были разные я был и конём Князя Владимира и балериной и валютной проституткой, я читал стихи, в лицах, ролях, меня уже никто об этом не просил, тамада слился в тихом ахере от происходящего, все буквально валялись под столами, жена плакала, но во мне проснулся давно мертвый актёр и Остапа было не остановить. Я придумывал сам конкурсы, сам же в них один за всех и участвовал, я пел, танцевал, искрометно шутил, потом темнота, утро телефон разрывается. Звонил жених, потом невеста, потом их родители и какие-то совершенно чужие голоса и номера, у них мол второй день, природа, шашлыки, но никто никуда не хочет ехать без меня.
Я поехал конечно, со мной здоровались незнакомые люди, целовали незнакомые женщины, обнимали и хлопали по спине незнакомые мужчины, а незнакомые дети лезли мне на руки, все смеялись, улыбались и говорили «ну ты блин даёшь конечно», день был долгий, все смеялись, жена плакала.
Касету я с той свадьбы так ни разу и не посмотрел, сколько не уговаривали, они её дома вместо «С легким паром» на НГ смотрят, всей семьёй. Я ухожу на кухню, пусть сами ржут.
P. S. В оправдание. Мне было 23 года, я был юн и неопытен.