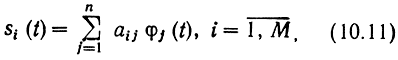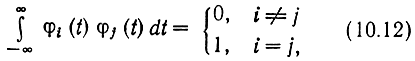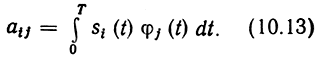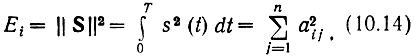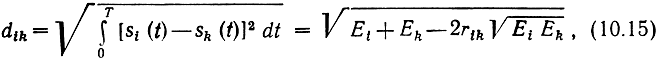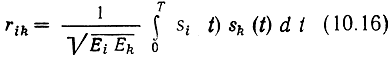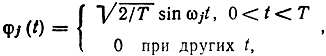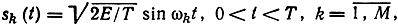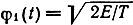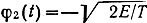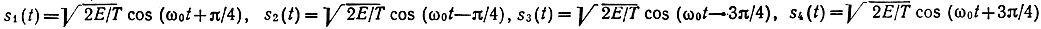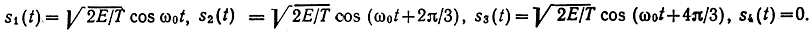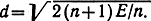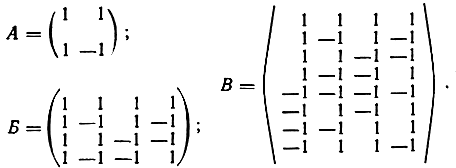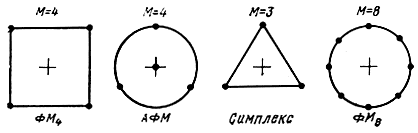коды делятся на двухпозиционные а 2 и многопозиционные а 2 где а
Коды в системах телемеханики
Классификация и характеристики кодов
В телемеханических системах сообщения передаются по схеме (рис.10).
Рисунок 10. Схема передачи сообщений
Конкретная совокупность импульсов тока, образующих линейный сигнал, называется кодовым словом или кодовой комбинацией. Множество кодовых слов, используемых для передачи сообщений, называется кодом.
В зависимости от длины кода n (число импульсов тока в кодовом слове) различают одноэлементные и многоэлементные коды. В одноэлементных кодах n = 1, и сообщение несет один импульс тока. Эти коды используют в системах телемеханики с разделительной и распределительной селекциями. В многоэлементных кодах n>1 и сообщение несут n- импульсов тока. Их используют при качественно-комбинационной и кодовой селекциях.
В зависимости от основания кода k (число качеств импульсов тока) различают двоичные (двухпозиционные) и многопозиционные коды. Двоичные коды имеют два качества импульсов тока (k=2). У многопозиционных кодов k>2. Наиболее распространены двоичные коды, так как они имеют наиболее простую кодирующую и декодирующую аппаратуру. В дальнейшем будем рассматривать двоичные коды и качества импульсов тока в них обозначать 0 и 1 (это могут быть отрицательная и положительная полярность, малая и большая амплитуда тока и др.).
Важнейшей особенностью кодов является их классификация по помехоустойчивости. По помехоустойчивости коды делятся на обыкновенные и корректирующие. Обыкновенные коды не обеспечивают защиту информации от искажений в результате воздействия помех в линиях связи. Например, на пункте управления формируется трехэлементное кодовое слово в двоичном коде с амплитудными качествами 010 (рис.11). Из-за помех в линии связи подавляется амплитуда второго импульса, и на контролируемый пункт поступает слово 000. В результате искажается информация и ложно включается объект 1 вместо объекта 3.
Рисунок 11. Искажение кодового слова
Корректирующие коды обеспечивают защиту от искажений (корректируют их). Так как борьба с помехами основная проблема теории кодирования, то все большое разнообразие кодов, используемых в современных системах телемеханики, связано с их различными корректирующими способностями. В дальнейшем именно с этой точки зрения будем рассматривать основные коды, которые нашли применение в системах железнодорожной автоматики и телемеханики.
По принципам построения кодовых комбинаций различают равномерные и неравномерные коды. Равномерными называются коды, у которых все кодовые комбинации состоят из одинакового числа элементов (n = const). Неравномерные коды содержат кодовые комбинации с различным числом разрядов, из-за чего возникают определенные сложности их реализации на практике. Поэтому в системах телемеханики нашли наибольшее распространение равномерные коды.
По закону кодообразования все коды делятся на избыточные и неизбыточные. К неизбыточным относятся коды, использующие все возможные комбинации, их часто называют простыми или первичными кодами. В избыточных кодах используется для передачи сообщений только часть всех возможных комбинаций, а оставшиеся комбинации используются для обнаружения или исправления ошибок, возникающих при передачи сообщений. Если в избыточном коде можно выделить разряды, предназначенные для передачи сообщения, и разряды, назначение которых обнаружение или исправление ошибок (контрольные разряды), то этот код называется разделимым. Если разряды кодового слова невозможно разделить на информационные и контрольные, то такой код называется неразделимым.
Для оценки кодов используют две основные характеристики:
Анализ методов обеспечения безошибочности передачи данных в сетях
Методы обеспечения безошибочности передачи данных
Для повышения достоверности и качества работы систем связи применяются групповые методы защиты от ошибок, избыточное кодирование и системы с обратной связью. На практике часто используют комбинированное сочетание этих способов.
Метод Вердана
К групповым методам защиты от ошибок можно отнести давно уже используемый в телеграфии способ, известный как принцип Вердана: вся информация (или отдельные кодовые комбинации) передается несколько раз, обычно не четное число раз (минимум три раза). Принимаемая информация запоминается специальным устройством и сравнивается. Суждение о правильности передачи выносится по совпадению большинства из принятой информации методами «два из трех», «три из пяти» и так далее. Например, кодовая комбинация 01101 при трехразовой передаче была частично искажена помехами, поэтому приемник принял следующие комбинации: 10101, 01110, 01001. В результате проверки каждой позиции отдельно правильной считается комбинация 01101.
Метод передачи информации блоками
Другой метод, также не требующий перекодирования информации, предполагает передачу информации блоками, состоящими из нескольких кодовых комбинаций. В конце каждого блока посылается информация, содержащая количественные характеристики переданного блока, например число единиц или нулей в блоке. На приемном конце эти характеристики вновь подсчитываются, сравниваются с переданными по каналу связи, и если они совпадают, то блок считается принятым правильно. При несовпадении количественных характеристик на передающую сторону посылается сигнал ошибки.
Помехоустойчивое кодирование
Помехоустойчивое кодирование предполагает разработку корректирующих (помехоустойчивых) кодов, обнаруживающих и исправляющих определенного рода ошибки, а также построение и реализацию кодирующих и декодирующих устройств.
Специалистами доказано, что при использовании помехоустойчивого кодирования вероятность неверной передачи во много раз снижается. Так, например, с помощью кода M из N, используемого фирмой IBM в вычислительных сетях, можно обнаружить в блоке, насчитывающем около тридцати двух тысяч символов, все ошибки, кратные трем или меньше, или пачки ошибок длиной до шестнадцати символов.
При передаче информации в зависимости от системы счисления коды могут быть двухпозиционными и многопозиционными. По степени помехозащищенности двухпозиционные коды делятся на обыкновенные и помехоустойчивые.
В помехоустойчивых кодах, кроме информационных элементов, всегда содержится один или несколько дополнительных элементов, являющихся проверочными и служащих для достижения более высокого качества передачи данных. Наличие в кодах избыточной информации позволяет обнаруживать и исправлять (или только обнаруживать) ошибки.
Основными среди многочисленных характеристик корректирующих кодов являются значность, корректирующая способность, избыточность и оптимальность кода, коэффициент обнаружения и исправления ошибки, простота технической реализации метода и другие. Так, значность кода, или длина кодовой комбинации, включает как информационные элементы m, так и проверочные (контрольные) k. Как правило, значность кода n равна m+k.
Оптимальность кода указывает на полноту использования его корректирующих возможностей.
Выбор корректирующих кодов в определенной степени зависит от требований, предъявляемых к достоверности передачи. Для правильного его выбора необходимо иметь статистические данные о закономерностях возникновения ошибок, их характере, численности и распределении во времени. Так, например, корректирующий код, исправляющий одиночные ошибки, может быть эффективен лишь при условии, что ошибки статистически независимы, а вероятность их появления не превышает некоторой величины. Этот код оказывается совершенно не пригодным, если ошибки появляются группами (пачками). Рекуррентные коды, исправляющие групповые ошибки, также могут оказаться неэффективными, если количество ошибок при передаче будет больше допустимой нормы.
Разработанные различные корректирующие коды подразделяются на непрерывные и блочные. В непрерывных, или рекуррентных, кодах контрольные элементы располагаются между информационными. В блочных кодах информация кодируется, передается и декодируется отдельными группами (блоками) равной длины.
Блочные коды бывают разделимые (все информационные и контрольные элементы размещаются на строго определенных позициях) и неразделимые (элементы кодовой комбинации не имеют четкого деления на избыточные и информационные). К неразделимым относится код с постоянным числом нулей и единиц.
Большие вычислительные системы (Amdal, IBM, Burroughs, ICL) используют очень сложную методику проверки ошибок при передаче по линиям связи между машинами. В ПЭВМ обычно применяется более простая техника проверки ошибок.
Необходимые сведения из теории кодирования
Длина кодовой комбинации – количество символов в комбинации, обозначаемое буквой n.
Представление информации кодом
Для примера рассмотрим простую систему с основанием m = 2 в виде обычного реле. Как известно, в реле может быть только два сигнала – либо контакт замкнут, либо разомкнут, соответственно передать можно только два сигнала – либо 1 когда контакт реле замкнут и на объекте присутствует напряжение, или 0, если контакт разомкнут, и напряжение на объекте нет. Ниже представлена система из шести реле и возможные кодовые комбинации при различных положениях реле:
Представленную выше систему часто используют для сигнализации. Например, нормальной работа системы будет считаться тогда, когда замкнуты все реле (комбинация 111111). Если на каком-то участке произошел сбой и контакт не был замкнут, то по сигналу легко определить на каком участке произошел сбой. Например, при комбинации 110111 понятно что проблема на участке с Р4, что значительно упрощает устранение причины отказа. Также такую информацию вполне возможно представлять в бумажном виде (распечатанном, например), на перфолентах, в цифровом виде.
Длина всех рассмотренных комбинаций в этом примере равна шести, то есть n = 6 (110111,101101 и так далее).
Также в кодовых комбинациях присутствует такое понятие как вес комбинации, который равен количеству единичных символов в коде и обозначается буквой l. Для комбинации 101101 вес l = 4, 111111 вес l = 6, 110111 вес l = 5.
Классификация кодов
Для удобства использования коды классифицируют. Рассмотрим основные классификации:
Очень часто в технике применяют код типа 2 из 5, имеющего число комбинаций:
У всех комбинаций присущ одинаковый вес l = 2.
Вес определенной n членной комбинации изменяющейся от 0 до n, в общем случае можно выразить биномом Ньютона:
Общее число комбинаций для n = 5:
Рассмотренный выше код (1.2) неполный, так как при его формировании было использовано только восемь комбинаций четного веса при возможных шестнадцати. Из оставшихся восьми нечетных комбинаций также можно сформировать неполный нечетный код.
Код 2 из 5 (1.1) – двухпеременный. Расстояние между смежными комбинациями в данном коде везде равно двум. Если те же комбинации расположить в другом порядке, то можно получить четырехпеременный код:
Если у кода отсутствуют арифметические свойства – он комбинаторный. Формирование комбинаторных кодов производят по законам теории соединений (перестановок, сочетаний, размещений), которая изучается в разделе математики называемом комбинаторикой. Из рассмотренных ранее кодов к комбинаторным относят нечетные, четные, равновесные.
Коды. Классификация кодов
При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией.
Совокупность кодовых комбинаций, обозначающих дискретные сообщения, называется кодом.
Множество возможных кодовых символов называется кодовым алфавитом, а их количество — основанием кода. В общем случае при основании кода т правила кодирования N элементов сообщения сводятся к правилам записи различных чисел в m-ичной системе счисления. Число символов и, образующих кодовую комбинацию, называется значностъю кода или длиной кодовой комбинации.
1)В зависимости от системы счисления, используемой при кодировании, различают двухпозиционные и многопозиционные коды. К первым относятся все коды, в которых используется двоичная система счисления. Часто эти коды называют двоичными. К многопозиционным кодам относятся все коды, в которых число позиций (основание кода) больше двух.
2)По числу элементов в системе различают равномерные и неравномерные коды.
Применение равномерных кодов упрощает построение автоматических буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями.
— Неравномерные коды характерны тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов 0 и 1, но и их количеством. Это приводит к тому, что различные кодовые комбинации имеют разную длительность. Типичным примером неравномерных кодов является код Морзе, в котором символы 0 и 1 используются только в двух сочетаниях: как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трем единицам — тире. Символ 0 используется как
знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как
разделительный знак между кодовыми комбинациями.
3)По помехоустойчивости коды делятся на обыкновенные и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются обыкновенными, или кодами без избыточности. В обыкновенных равномерных кодах превращение одного символа комбинации в другой, например, 1 в 0 или 0 в 1, приводит к появлению новой возможной комбинации, т. е. к ошибке. Корректирующие коды строятся так, что для передачи сообщения используются не все возможные кодовые комбинации, а лишь некоторая их часть. Тем самым создается возможность обнаружить и исправлять ошибки при неправильном воспроизведении некоторого числа символов. Корректирующие свойства кодов достигаются ценой введения в кодовые комбинации дополнительных (избыточных) символов.
4) Корректирующие коды можно разделить на блочные и непрерывные. Корректирующий код называется блочным, если каждая его комбинация имеет ограниченную длину, и непрерывным, если его комбинация имеет неограниченную, а точнее, полубесконечную длину.
6)По разделению на разделимые и неразделимые.
Коды делятся на двухпозиционные а 2 и многопозиционные а 2 где а
10.3. Многопозиционные сигналы и корректирующие коды
Ансамбль сигналов
Геометрически каждому сигналу ансамбля соответствует точка (или ректор) в n-мерном пространстве с координатами (ai1, ai2. ain i = 1. М. Энергия сигнала при этом равна квадрату
а расстояние между сигналами
— коэффициент взаимной корреляции рассматриваемых сигналов. В дальнейшем будем рассматривать ансамбли сигналов с одинаковыми энергиями Ei = Ek = E.
Наиболее распространенными многопозиционными сигналами являются ортогональные, биортогональные и симплексные. Если сигнальные точки выбрать на линиях, совпадающих с ортами φ на расстояниях √E от начала координат, то получим систему ортогональных сигналов. Число сигналов в таком ансамбле М = n. Так, если принять
Ортогональные сигналы образуют эквидистантную систему, расстояния между любыми двумя сигнальными точками которой одинаковы и, согласно выражению (10.15), равны d = √2E. Биортогональные сигналы образуются по следующему правилу: к каждому ортогональному сигналу добавляется противоположный. Здесь число сигналов М = 2n. Простейшим из биортогональных
является ансамбль с М = 4. Сигналы имеют одинаковые энергии и находятся на одинаковом расстоянии от начала координат. На (плоскости они образуют квадрат (рис. 10.4). При выборе в качестве базисных функций
Известные сигналы с амплитудно-фазовой модуляцией (АФМ) образуют круговую сеть (см. рис. 10.4): например, три сигнала равномерно распределены по окружности, а четвертый расположен в центре окружности. В том же базисе они могут быть представлены так:
Многопоэиционные сигналы с фазовой модуляцией (ФМ) образуют круговую сеть с равномерным распределением точек по окружности. Построить ансамбли ортогональных и биортогональных многопозиционных сигналов можно и на основе двоичных последовательностей. Для этого обычно используют элементарную матрицу Адамара А, повторением которой трижды в позитивной и один раз в негативной форме можно увеличить размеры матрицы каждый раз вдвое и получить матрицу Б, которая представляет ансамбль ортогональных сигналов с М = 4:
Каждая строка этой матрицы (последовательность двоичных символов) образует один сигнал. Нетрудно проверить, что эти строки (сигналы) взаимноортогональны. Дополняя матрицу Б инверсиями строк, получим матрицу В, представляющую ансамбль М = 8 биортогональных сигналов. Аналогично строятся ансамбли с большим числом сигналов М. Симплексные сигналы также могут быть получены на основе двоичных последовательностей [12].
Рис. 10.4. Примеры ансамблей двумерных сигналов
Помехоустойчивость систем связи в общем случае зависит как от вида передаваемых сигналов, так и от способа приема. При оптимальном приеме реализуется потенциальная помехоустойчивость. Алгоритм оптимального приема М-позиционных сигналов определяется системой неравенств (6.23), а вероятность ошибки вычисляется как вероятность невыполнения этих неравенств.
В § 6.5 получены выражения для вероятности ошибки при М = 2. Для не двоичных систем (М>2) получить такие простые выражения не всегда удается. Для некоторых ансамблей сигналов такие формулы имеются в [8], а для других, путем численного интегрирования, получены графики зависимости p = f(E/N0) [12, 18], которые ниже используются для вычисления энергетической эффективности р. Для приближенных вычислений при симметричных системах можно воспользоваться верхней оценкой (6.60)
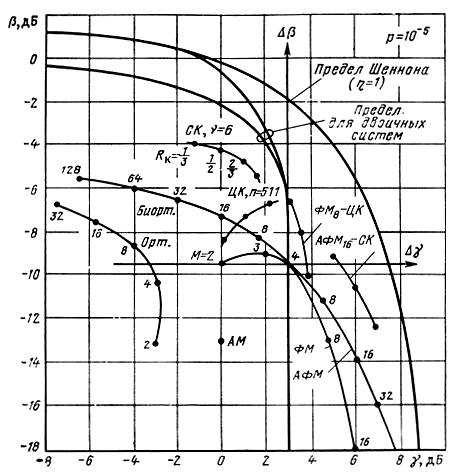
Различают два класса многопозиционных сигналов. Первый образуют «плотные» сигналы, когда с ростом объема ансамбля М при фиксированной размерности n расстояние между сигналами уменьшается, а удельная скорость γ, согласно (10.18) возрастает при соответствующем снижении энергетической эффективности β. В качестве примера таких сигналов на рис. 10.5 приведены кривые для многопозиционных сигналов ФМ и АФМ.
Рис. 10.5. Кривые энергетической и частотной эффективности систем с многопозиционными сигналами и корректирующими кодами
Приведенные на рис. 10.5 βγ-диаграммы позволяют количественно оценить обменный выигрыш (проигрыш) различных систем. Так, например, применение биортогональных сигналов с М = 16 позволяет получить энергетический выигрыш Др = 2,4 дБ в обмен на снижение удельной скорости γ в 2 раза (3 дБ). Обмен энергетической эффективности на частотную можно осуществить с помощью многопозиционных сигналов с ФМ. Однако более эффективными являются АФМ сигналы.
Расчетные кривые на рис. 10.5 показывают, что применение циклического кода в канале с ФМ или сверточного кода в канале с АФМ позволяет получить одновременно выигрыш как по энергетической, так и по частотной эффективности или во всяком случае выигрыш по одному показателю без ухудшения другого. Построение таких высокоэффективных систем (η>0,5) на основе сложных сигнально-кодовых конструкций ведет к неизбежному увеличению сложности системы. Не пропускная способность (предел Шеннона), а сложность является ограничивающим фактором при построении высокоэффективных систем. Задача состоит в том, чтобы построить систему удовлетворяющую высоким показателям эффективности, при минимальной (допустимой) сложности, а следовательно, и стоимости системы.