Ragdoll анимация что это
Советы по анимированию рэгдолл-персонажей Статьи редакции
Главное — найти баланс веса и сопротивления у разных частей тела.
Инди-разработчик Лоркан МакГэрри-Хант опубликовал на Gamasutra текст, в котором дал несколько советов, как анимировать рэгдолл-персонажей в своей игре. Подход автора основывается на тонкой настройке веса отдельных частей тела персонажа. А для усложнения анимации МакГэрри-Хант советует использовать инверсную кинематику. Выбрали из материала главное.
Особенность рэгдолл-персонажей заключается в том, что их анимация не просчитана заранее — движения зависят от физики частей тела и рассчитываются прямо во время геймплея. Чтобы анимация выглядела правдоподобной, важно учитывать импульс и вес объектов. Именно поэтому для получения корректного результата нужно постоянно экспериментировать с физикой тела.
В рэгдолл-анимации любое простое действие требует взвешенного подхода. Чтобы пойти вперёд, персонаж должен поднять ногу и переставить её в сторону цели — когда обе ноги будут на земле, это же действие должно произойти со второй ногой.
Если же вы хотите, чтобы персонаж ударил кулаком, то для правдоподобного эффекта нужно немного изменить вес рук — в момент удара надо увеличить массу на несколько кадров, чтобы тело последовало за кулаком. Такая «физичность» придаст реалистичности действиям.
При настройке вашего рэгдолл-персонажа важно правильно определить вес и сопротивление различных частей тела. Если сопротивление будет слишком высоким, то герой будет похож на малоподвижную фигурку. Если же оно будет слишком низким, то персонаж будет подобен мягкой тряпичной кукле.
МакГэрри-Хант советует создать скрипт для управления сопротивлением, который позволит установить общий вес персонажа, а затем определить, какую долю от общего значения занимает каждая часть. Это позволит быстро изменять и тестировать различные настройки, чтобы найти идеальный баланс.
По словам разработчика, чтобы анимация выглядела хорошо, вам нужно сделать кастомный скрипт гравитации — компоненты rigidbody, которые доступны по умолчанию, не подойдут для этого. У вас обязательно должна быть возможность менять центр масс — это даст больше контроля над позой.
Если вы будете поддерживать и тянуть туловище персонажа вверх, то это поможет сделать его движения менее кукольными. Но при этом важно не переусердствовать — если вы это допустите, то при падении персонаж будет вести себя так, словно плывёт в плотной жидкости.
По словам МакГэрри-Ханта, если вы хотите упростить задачу, устраните соединительные части вашего персонажа — оставьте только торс и крайние точки конечностей (кисти и стопы). Чтобы они не болтались в воздухе, соедините части, к примеру, пружиной, движения которой просчитываются при помощи инверсной кинематики.
Разработчик отметил, что принципы инверсной кинематики позволят вам сделать анимацию более комплексной и правдоподобной. Поэтому их можно использовать вместо описанного подхода, учитывающего вес конечностей.
Рэгдолл
 | Вкратце Персонаж падает не запрограммированной анимацией, а физической моделью, со всеми глюками упрощённой игровой физики. |
Рэгдолл («тряпичная кукла») — способ компьютерной анимации в трехмерных играх, при котором движение персонажа (преимущественно во время полета и свободного падения) является не набором заранее отрендеренных анимаций, а попыткой воспроизведения физики в реальном времени. Для этого используется набор сегментов, соответствующих определенным частям тела (голова, туловище, конечности) и связующих их суставов-шарниров. Также наличествует определенная система ограничений, задающая порядок движения для каждого сегмента, и способствующая повышению общей реалистичности — например, нельзя позволять вращаться коленным или тазовым суставам на 360°.
Главная фишка рэгдолла, откуда, собственно, и пошло название — при воспроизведении движения, особенно если приходится натыкаться на различные препятствия, персонаж может принимать самые несуразные позы, подобно настоящей тряпичной кукле. Это связано с некорректной работой системы сочленений, ибо в реальной жизни суставы и мышцы имеют определенную жесткость, в отличие от компьютерной модели, где ее либо вовсе нет, либо она не сопоставима с реальной.
История возникновения Ragdoll-физики.
Приветствую всех Стопгеймовцев. Тему для блога я подобрал просто: сидел я и играл в Max Payne на своем смарте, как вдруг вспомнил про вторую часть этой игры, и про замечательную Ragdoll-физику в ней. Начал рыться в интернете в поисках информации, узнал немало, и поэтому я решил создать тему, где постараюсь тщательно рассказать об истории появления этой замечательной технологии, без которой не обходится ни одна игра современности.
Для начала немного теории. Физика Ragdoll — вид процедурной анимации, пришедший на замену статичной, пререндерной анимации.
Здесь мы можем наблюдать раннюю модель использования Ragdoll. 1997 год
Ранние трёхмерные компьютерные игры использовали заранее созданную анимацию для отображения смерти персонажей. Конечно, никто не собирался делать тысячу анимаций смерти, да и слишком муторная это была работа. Поэтому нам сейчас кажется диким, когда в игре вместо Ragdoll’a заранее созданные анимации, но в то время никто не жаловался, ибо компьютерная мощь не была столь велика, чтобы в реальном времени создавать анимацию смерти. Когда же компьютеры стали мощнее, появились и первые задатки Ragdoll’a с некоторыми ограничениями.
Физику Ragdoll в народе называют «тряпичной куклой», такое название произошло из-за некорректной работы системы сочленений, в связи с ограничениями реализации некоторые суставы модели имели малую или отсутствующую жёсткость, что заставляло её падать подобно настоящей тряпичной кукле, нередко вызывая комический эффект несуразностью получившейся позы.
Первой игрой с физикой Ragdoll для меня стала Hitman: Codename 47, но там физика имела другую формулу, нежели привычный Ragdoll, о нем мы поговорим позже.
Помимо Ragdoll’a игра еще обладала рядом интересных качеств. Например: в игре не было интерфейса, целиться нужно было с помощью мушки, количество патронов героиня произносила вслух при выстреле, ну а количество здоровья можно было узнать по татуировке в виде сердца на груди героини.
На данный момент игра не забыта, есть даже специальный фанатский сайт, где можно найти кучу информации и модов на эту игру, создается даже ремейк на движке CryEngine 3.
Ну а мы перейдем к следующему разделу повествования.
Технология ragdoll работает, основываясь на принципах алгоритма Физерстоуна и пружинно-амортизаторных контактов. Существует также альтернативное решение, использующее систему ограничений и идеализированные контакты. В то время, как ограниченно твёрдые тела достаточно близки к «тряпичной кукле», существуют и «псевдо-ragdoll» технологии.
1. Интегрирование Верле.
Использовалось в игре Hitman: Codename 47 и стало распространено благодаря Томасу Якобсону. В этой технике каждая кость персонажа моделируется как точка, соединённая с произвольным числом других точек через простые ограничения. Ограничения Верле намного проще и гораздо быстрее вычисляются, чем те, которые используются в системе полностью смоделированного твердого тела, что выражается в меньших затратах процессора.
2. Инверсная кинематика
Относится к технологиям пост-обработки (англ. post-processing) и использовалась в Halo: Combat Evolved. Используя заранее созданную анимацию смерти, игровой движок просчитывает финальное положение тела, которое удовлетворяло бы реалистичному отображению. В случае применения инверсной кинематики умирающие персонажи могут частично проходить сквозь геометрию мира, однако в итоге все кости модели будут лежать на допустимом месте.
Если Мастер Чиф выстрелит в труп, он шевельнется подобно Рэгдоллу.
4.Процедурная анимация (NaturalMotion)
Изначально подобные технологии использовались в создании фильмов, рекламных роликов и телепрограмм, но со временем нашли своё применение и в компьютерных играх. Ключевым элементом этой процедурной анимации является расширенная симуляция человеческого тела. Технология Euphoria при обработке анимации воспроизводит не только кости, но и мускулы и нервную систему, добавляя в сцену правильное взаимодействие с окружающим миром. За счёт этого, каждый новый показ сцены отличается от предыдущего, что повышает увлекательность повторного прохождения игры. Действие технологии NaturalMotion можно увидеть в GTA IV и Star Wars: The Force Unleashed. 
В современном мире компьютеры уже достаточно сильны и с легкостью переваривают «Куколку», поэтому это даже менее затратно, чем писать заранее продуманные анимации, ведь технология просчитывает все в реальном времени. С каждым разом Ragdoll усовершенствуется, становясь более реалистичным. Использование новейших технологий, основанных на ragdoll-анимации, можно увидеть в таких играх, как Grand Theft Auto IV от Rockstar Games, Indiana Jones and the Staff of Kings и Star Wars: The Force Unleashed от LucasArts.
Основой всех основ «Кукольной физики» являются простейшие варианты соединения.
Видов соединения в основном выделяют два, это Шариковое соединение:
и Шарнирное соединение:
Конечно, технологии Ragdoll’a везде разные, но эти два способа соединения по сути являются основой нормальной физики тел.
Значение в игровой индустрии.
Естественно, Ragdoll играет немаловажную роль в индустрии игр. Ее роль доходит аж до того, что создаются целые игры, которые полностью основываются на технологии «Куклы из тряпки». Например: Файтинг Rag Doll Kung Fu. Игрок волен махать своими руками и ногами в различные стороны, естественно, используя физику Ragdoll. На экране творится полная ахинея: игроки летят через весь экран, перелетают друг друга, выполняют сумасшедшие комбо ногами, буквально вдавливая друг друга в землю, выглядит и вправду зрелищно. Более простой аналог файтинга с использованием данной технологии игра под названием Ragdoll masters, управление здесь заметно проще, нежели в первом варианте: если в Rag Doll Kung Fu игрок отвечал за каждую конечность отдельно, то в Ragdoll masters — за все тело целиком, поэтому он беден на эффектные комбо, но это восполняется простотой управления, игрой на двух игроков(Один через мышь, другой — WASD), и скоростью игры, а она быстрая, очень быстрая.
Так же Ragdoll играл немаловажное значение в гоночных аркадах. На ум сразу приходит сумасшедшая гоночная серия FlatOut. По сути это была обычная аркада, с хорошей разрушаемостью автомобилей, но в игре также были мини-игры, некоторые из них были основаны как раз таки на Ragdoll. Суть таких мини-игр была проста: вам нужно на максимальной скорости врезаться в бордюр, в следствие чего уже мертвый водитель вылетает из лобового стекла, меняя траекторию тушки бедолаги его нужно забросить как можно выше. 
Известны также такие игры как Stair Dismount и Truck Dismount, в которых Ragdoll-физика стала основой геймплея. В обеих играх смысл сводился к тому, чтоб причинить больше увечий нашей «тряпичной кукле»
Отдельного упоминания также заслуживает игра Toribash. Это по своей сути пошаговый файтинг на основе физики «Рэгдолл». Игра вышла в 2006 году и была создана всего лишь одним человеком — шведом Хампусом Сёдерстрёмом. Игра распространяется бесплатно и по состоянию на 2013 год продолжает развиваться и периодически обновляться. Также была выпущена версия для Wii, которая отличается от оригинала менее качественной графикой и измененными звуками. В 2012 году также была создана упрощённая 2D-версия игры под названием Minibash, распостраняющаяся на платформах iOS и Android.
Управление в игре осуществляется изменением положения (расслаблением, напряжением, сгибанием, разгибанием, вращением и наклонением) суставов отображаемой на экране куклы. Также можно сделать ладони «липкими» и схватиться за противника. Нажимая пробел, игрок делает ход и продвигает время на определенное количество фреймов (по умолчанию 10). Когда при правильных манипуляциях одна кукла бьёт другую, то, при достаточном нанесении ущерба, часть тела может оторваться или сломаться. Правильно управляя куклой, можно выполнять довольно сложные атаки. Есть также много различных модов, как официальных, так и созданных игроками. Эти моды могут изменить вид куклы, воздействовать на её движение, а также добавить новые объекты к окружению.
Ragdoll уже в вашем кармане.
Мощность смартфонов и планшетов растет все быстрее и быстрее. Буквально несколько лет назад никто и представить не мог, что ragdoll сможет работать и на смартфонах, об этом просто не думали. Сейчас даже средненький смартфон или планшет легко и без тормозов запускает игры с Ragdoll-физикой. Конечно, не все «карманные развлекухи» имеют такую поддержку, но все же есть некоторые разработчики игр, которые в особенностях своей игрушки гордо приписывают надпись: «Поддержка Ragdoll-физики!». Приведу вам несколько примеров игр с данной физикой.
Знаете ли вы.
что в игре Crysis отсутствует физика Ragdoll, хотя она поддерживается движком и даже включена в его официальную спецификацию. Очевидно, это связано с желанием разработчиков уменьшить возрастные рейтинги игры. Несмотря на то, что анимация «тряпичной куклы» в игре отключена, после выхода игры были выпущены модификации, которые её включают.
На этом я заканчиваю свой блог, возможно, я обновлю его, когда найду еще что-нибудь интересное по теме Ragdoll’a. Всем Стопгеймовцам желаю успехов во всех делах, и конечно: играйте только в хорошие игры!
Введение в процедурную анимацию
В этой серии статей мы познакомимся с инверсной кинематикой в видеоиграх. Перед началом нашего путешествия я расскажу о нескольких играх, в которых используются процедурные анимации, и о том, чем они отличаются от традиционных, основанных на ресурсах, анимаций.
Серия будет состоять из следующих частей:
Часть 1. Введение в процедурную анимацию
В большинстве игр анимации персонажей являются «статичными». Когда персонаж двигается на экране, художник создаёт конкретное движение. Они изготавливаются вручную или записываются с помощью захвата движений. Анимации в этом случае — это заранее созданные ресурсы. Когда персонажу нужно выполнить другое действие, требуется другая анимация. Такой способ реализации движения персонажей довольно стандартен для индустрии игр. Существуют большие и подробные коллекции анимации, в которых есть наиболее часто используемые поведения, такие как ходьба, прыжки и стрельба. Традиционные анимации доминируют в игровой индустрии, однако у них есть равноценные альтернативы. Я хочу познакомить вас с концепцией процедурных анимаций.
Главная мысль здесь заключается в том, что моменты состояния персонажа можно генерировать процедурно. В одной из самых стандартных техник генерирования процедурных анимаций используется симуляция физики. Поэтому её часто называют физической анимацией (Wikipedia). Типичный пример — это вода. Можно анимировать её вручную или использовать анимацию, учитывающую динамику жидкостей.
Ниже мы обсудим очень специфический подвид физических анимаций, в котором применяется симуляция твёрдых тел (rigid body simulation). Такой же тип симуляции обычно используется в игровых движках, например в Unity и Unreal. Давайте посмотрим, как этот простой принцип используется в играх для создания физических анимаций.
Ragdoll-физика
В самой основе физических анимаций лежит принцип возможности симуляции движения персонажей. Воссоздавая процессы и ограничения, управляющие человеческим телом, можно приблизиться к созданию реалистичных поведений. Один из простейших, но эффективных способов создания процедурных анимаций — применение физики тряпичной куклы (рэгдолла, ragdoll)(Wikipedia). Идея заключается в создании гуманоидного тела и соединения всех его звеньев сочленениями (joints) для воссоздания степеней свободы, демонстрируемых реальным прототипом. Просто используя физику твёрдых тел и ограничения сочленений, можно симулировать падение тела человека. Это не только позволяет сэкономить деньги на «анимацию смерти». Также это позволяет создавать персонажей, реалистично падающих и взаимодействующих с окружениями. Подобную задачу почти невозможно решить с помощью только готового набора анимаций, вне зависимости от его точности.
Важнейший недостаток рэгдоллов — их огромная непредсказуемость, которая часто приводит к очень забавным поведениям.
Сегодня рэгдоллы очень привычны в играх. В Unity есть простой инструмент Ragdoll Wizard, позволяющий быстро превратить гуманоидную модель в рэгдолл.
Симуляции твёрдого тела
Основная проблема рэгдоллов — отсутствие управления движениями. Если соединить части тела сочленениями, то персонаж не сможет ни ходить, ни прыгать. Он будет только падать. Однако бывают ситуации, в которых можно использовать смешанный подход.
В статье How Grow Home Uses Maths To Generate Personality игровой журналист Алекс Уилтшир (Alex Wiltshire) разговаривает с представителями Ubisoft об игре Grow Home. Одна из основных особенностей игры — способ движения главного героя, Бада (BUD). В игре нет готовых анимаций, по крайней мере, в традиционном смысле. Когда игрок двигается, положение ног и рук управляется кодом. Части тела подвержены тем же ограничениями, что и у рэгдолла, что заставляет их создавать убедительные анимации.
Подобный принцип также активно используется в Rain World. Каждое животное в игре имеет тело, состоящее из нескольких коллайдеров. Некоторые из них управляются кодом, другие контролируются сочленениями. Это можно заметить на анимации внизу. Конечные точки крыльев хищной птицы движутся программно, остальные кости соединены шарнирами. Управление конечными точками автоматически создаёт плавную анимацию, которую иначе достигнуть бы не удалось.
И в Grow Home, и в Rain World процедурные анимации используются для повышения реалистичности персонажей. Однако контроллеры не полагаются на эти анимации. В игре Gang Beasts эта концепция развита ещё дальше. Игра полностью одобряет разболтанные движения, возникающие в результате использования ragdoll-физики. В результате получились забавные персонажи с непредсказуемыми движениями.
Инверсная кинематика
Симуляции твёрдого тела позволяют упростить создание анимаций. Мы указываем, где должны находиться руки и ноги Бада, а всё остальное делает за нас физический движок. Этот очень простой подход работает с простыми персонажами, но ему часто недостаёт реализма. В симуляциях твёрдого тела принимаются в расчёт только такие параметры, как гравитация и масса, но им не хватает знания контекста. Во многих случаях требуется создать что-то, действующее не только под воздействием ограничений, обусловленных гравитацией и соединениями.
Следующий шаг в создании процедурных анимаций известен как инверсная кинематика. Для рэгдолла любого типа инверсная кинематика вычисляет, как его нужно двигать, чтобы достичь нужной цели. В Grow Home и Rain World физика сама определяет, как должны двигаться подверженные воздействию гравитации соединения. Инверсная кинематика заставляет их двигаться в нужных фазах.
Одной из первых инди-игр, в которых активно использовалась эта концепция, стала The Majesty Of Color студии Future Proof Games. В ней игрок управляет щупальцем морского существа. В отличие от крыла птицы из Rain World, это щупальце не просто управляется шарнирами. Каждый сегмент поворачивается таким образом, чтобы конечная точка щупальца достигла нужной точки. Если бы в этой анимации использовалась только симуляция твёрдого тела, то щупальце казалось бы «приколотым» к этой точке, как кусок верёвки.
Инверсную кинематику можно использовать для решения множества задач. Наиболее стандартные — это естественное движение гуманоидных персонажей к определённым объектам. Вместо использования заранее заданных анимаций, разработчики просто указывают цель, которой должна достичь рука. Всё остальное делает инверсная кинематика, находящая наиболее естественный способ движения соединений руки. Если бы использовалась только симуляция твёрдого тела, то движение было бы судорожным, казалось бы, что части тела просто перетаскивают.
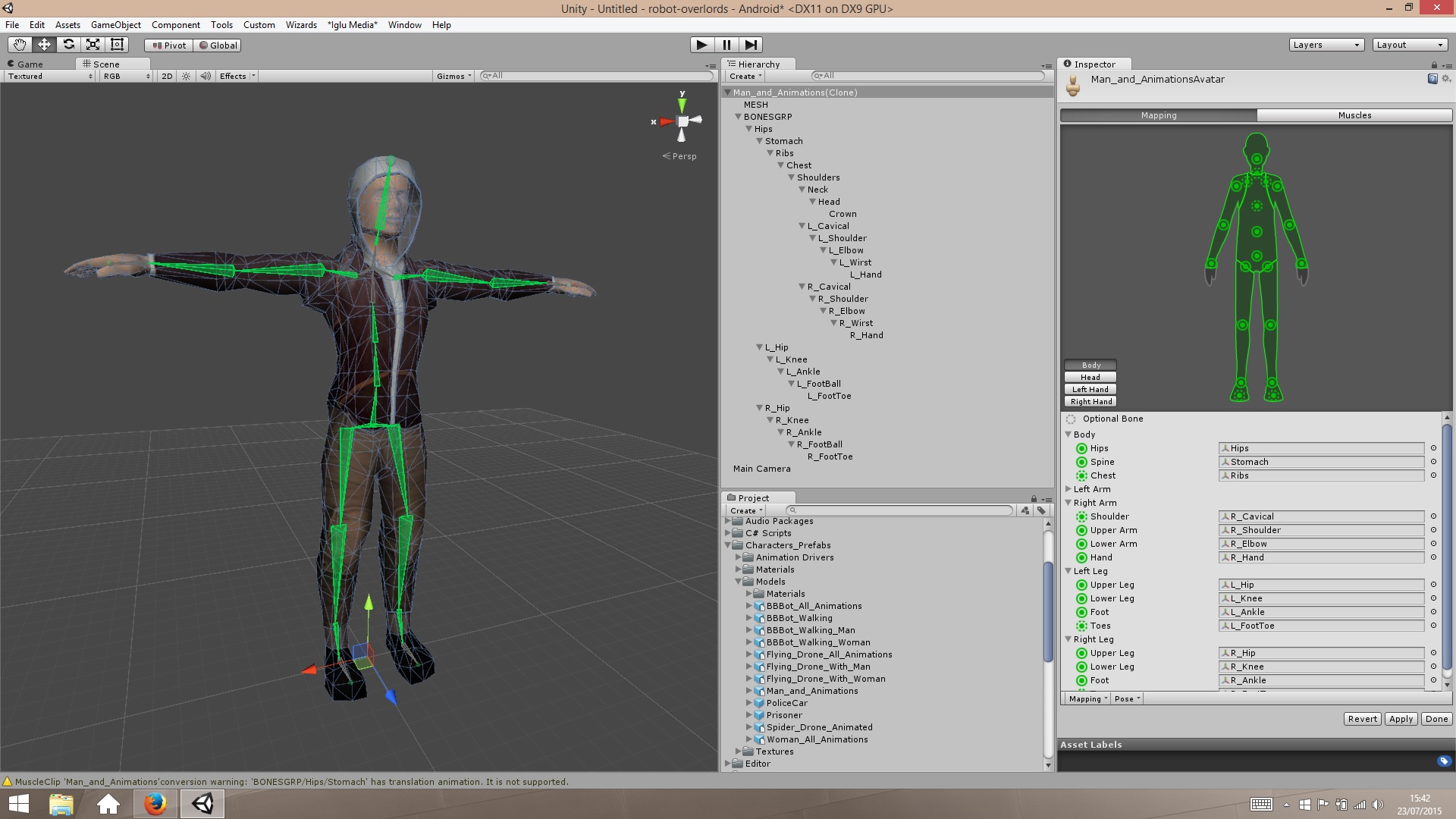
В редакторе анимаций Unity под названием Mechanim есть инструмент (справка Unity), позволяющий разработчику использовать для гуманоидных персонажей инверсную кинематику.
В оставшейся части этой серии статей я сосредоточусь на решении проблемы инверсной кинематики. Мы разберёмся, как можно управлять роботом-манипулятором или щупальцем монстра.
Часть 2. Математика прямой кинематики
Теперь мы начнём путешествие в мир инверсной кинематики. Есть множество способов решения этой проблемы, но все они начинаются с прямой кинематики.
Инверсная кинематика берёт точку в пространстве и сообщает нам, как нужно двигать рукой, чтобы достичь её. Прямая кинематика решает противоположную двойственную задачу. Зная, как мы будем двигать руку, она сообщает нам, какой точки пространства достигнет рука.
Робот-манипулятор
Инверсная кинематика изначально применялась для управления роботами-манипуляторами. Поэтому в этой серии статей будут использоваться допущения и терминология робототехники. Однако это никак не ограничивает возможные варианты применений инверсной кинематики. Вы можете использовать её для человеческих рук, лап пауков и щупалец.
Во-первых, давайте начнём с демонстрации того, что мы понимаем под термином «робот-манипулятор»:
На изображении выше показан стандартный робот-манипулятор, изготовленный из «звеньев» (limbs), соединённых «сочленениями» (joints). Так как показанный на изображении робот имеет пять независимых сочленений, то считается, что у него есть пять степеней свободы. Каждое сочленение управляется двигателем, позволяющим перемещать присоединённое к сочленению звено на определённый угол.
Чтобы рассмотреть более общий пример, мы можем начертить схему сочленений. В этой статье мы примем, что каждое сочленение может поворачиваться только по одной оси.
Инструмент, прикреплённый к концу робота-манипулятора, называется конечным звеном. В зависимости от контекста он может считаться или не считаться одной степенью свободы. В этой статье конечное звено не будет учитываться, потому что мы сосредоточимся только на движении для достижения нужной точки.
Прямая кинематика
В этом примере каждое сочленение может поворачиваться по одной оси. Поэтому состояние каждого сочленения измеряется как угол. Поворачивая каждое сочленение на определённый угол, мы позволяем конечному звену достигать разных точек в пространстве. Определение того, где находится конечное звено при известных углах сочленений, называется прямой кинематикой.
Прямая кинематика — это «простая» проблема. Она означает, что для каждого множества углов существует один единственный результат, который можно вычислить без всяких неопределённостей. Определение того, как робот-манипулятор двигается в зависимости от передаваемых нами данных — это необходимый шаг для нахождения обратной проблемы инверсной кинематики.
Геометрическая интерпретация
Прежде чем начать писать код, нам нужно понять математические построения, стоящие за прямой кинематикой. Но прежде всего нам нужно разобраться, что она значит пространственно и геометрически.
Поскольку визуализировать повороты в 3D не так просто, давайте начнём с простого манипулятора в двухмерном пространстве. Робот-манипулятор имеет «исходное положение» — это конфигурация, в которой все сочленения повёрнуты на их «нулевой угол».
На схеме выше показан манипулятор с тремя степенями свободы. Каждое сочленение повёрнуто в положение его нулевого угла, то есть робот находится в исходном положении. Мы можем увидеть, как изменяется такая конфигурация при повороте сочленения на градусов. Он приводит к соответствующему перемещению всей цепочки сочленений и звеньев, прикреплённых к .
Важно заметить, что двигатели, прикреплённые к другим сочленениям, пока не двигались. Каждое сочленение вносит свой вклад в локальный поворот прямой цепочки связей. На схеме ниже показано изменение конфигурации при повороте второго сочленения на градусов.
Положение определяет только , а на воздействуют уже и , и . Система координат поворота (красная и синяя стрелки) ориентирована в соответствии с суммой поворотов более ранней цепи соединений, к которой она присоединена.
Математика
Из предыдущих схем очевидно, что для решения проблемы прямой кинематики нам нужно вычислить положение вложенных (подчинённых) объектов при их повороте.
Давайте посмотрим, как его вычислить на примере двух сочленений. Найдя решение для двух элементов, мы можем повторять этот процесс для решения цепей любой длины.
Начнём с простого случая, когда первое сочленение находится в своём начальном положении. Это значит, что , как на схеме ниже:
Когда не равен нулю, нам нужно просто повернуть вектор расстояния в точке опоры вокруг на градусов:
Математически это можно записать как:
Ниже мы узнаем, как можно использовать функцию AngleAxis (документация Unity) без возни с тригонометрией.
Воспроизводя ту же логику, мы можем получить уравнение для :
И, наконец, общее уравнение:
В следующей части статьи мы увидим, как это уравнение удобно реализовать в коде на C#.
Если вы знакомы с вращением в 2D, то это можно сделать тригонометрически:
О выводе уравнения можно почитать в моей статье A Gentle Primer on 2D Rotations.
Если вы обладаете инженерными знаниями, то могли решать эту проблему иначе. Проблемы прямой и обратной кинематики широко известны, и для их решения существует несколько стандартизированных подходов. Один из них — привязка к каждому сочленению четырёх параметров, называемых параметрами Денавита-Хартенберга (Wikipedia). С ними удобно работать в матричном формате и они отлично подходят для аналитического решения проблемы инверсной кинематики.
Однако в этой статье мы их не используем. Решение матрицы Денавита-Хартенберга требует больше математики, чем многие программисты захотят разбираться. Выбранный мной подход использует градиентный спуск, который является более общим алгоритмом оптимизации.
Часть 3. Реализация прямой кинематики
В этой части мы продолжим решать проблему прямой кинематики. Найдя в прошлой части математическое решение, теперь мы узнаем, как реализовать его в коде на C# для Unity. В следующей части, «Введение в градиентный спуск», мы наконец покажем теоретические обоснования для решения проблемы инверсной кинематики.
Введение
В предыдущей части мы формализировали движение робота-манипулятора. Мы начали с простого примера из трёх сочленений. В своих исходных положениях они имеют изображённую ниже конфигурацию:
Разные на схеме представляют собой декартовы координаты, или -тое сочленение. Локальные углы, определяющие поворот относительно исходных положений, помечены как .
При повороте сочленений мы наблюдаем следующую картину:
Поведение этой системы можно суммировать следующими утверждениями:
С учётом всего вышесказанного, мы можем начать придумывать возможный способ реализации этих поведений в Unity.
Иерархия GameObject
В Unity уже есть способ реализации всех вышеупомянутых требований: система родительских компонентов (parenting). Если сделать игровой объект дочерним по отношению к другому, он автоматически наследует положение, поворот и масштаб.
Если вам знаком риггинг, то вас это не удивит. Кости, представляющие собой сочленения гуманоидного персонажа, тоже имеют систему родителей, при которой повороты и движения наследуются. На изображении из Unity Animation 3: Character Setup Майкла Эрбетнота показан очевидный пример этого.
При создании иерархии соединений необходимо убедиться, что, когда все локальные углы Эйлера равны нулю, то робот-манипулятор находится в исходном положении. Для гуманоидного персонажа это обычно стандартная T-образная поза, показанная на изображении выше.
Реализация
Возможность создания дочерних компонентов в Unity де-факто решает проблему прямой кинематики. К сожалению, этого недостаточно. В следующей части серии статей мы увидим, что нам на самом деле нужен способ проверки положения конечного звена без перемещения робота-манипулятора. Это заставит нас по-своему реализовать эту базовую функцию Unity.
Первый шаг — это сохранение информации о каждом из сочленений робота-манипулятора. Этого можно достичь при помощи скрипта, например RobotJoint из следующего примера:
Повороты в Unity часто описываются через углы Эйлера. Это три числа, соотвествующие повороту объекта по осям X, Y и Z. Углы Эйлера обозначают крен (roll), тангаж (pitch) и рыскание (yaw) объекта в пространстве. Однако с математической точки зрения использование углов Эйлера может привести к довольно неприятным проблемам.
Работать с углами удобнее с помощью кватернионов (quaternions). Кватернионы — это математические объекты, которые можно использовать для описания поворотов. В отличие от них, углы Эйлера описывают ориентацию. Квартернион описывает путь, который нужно пройти из одной ориентации в другую. С технической точки зрения, это слишком большое упрощение, но для нашей статьи его более чем достаточно.
Вращения ⇔ кватернионы
Добавление вращений ⇔ умножение кватернионов
При умножении двух кватернионов создаётся новый кватернион, включающий в себя оба поворота. При каждой итерации цикла for переменная rotation умножается на текущий кватернион. Это значит, что она будет включать в себя все повороты всех сочленений.
Кватернион * вектор = повёрнутый вектор
Наконец, кватернионы используются в этой строке:
Она полностью соответствует следующей записи:
Произведение кватерниона и вектора применяет поворот.