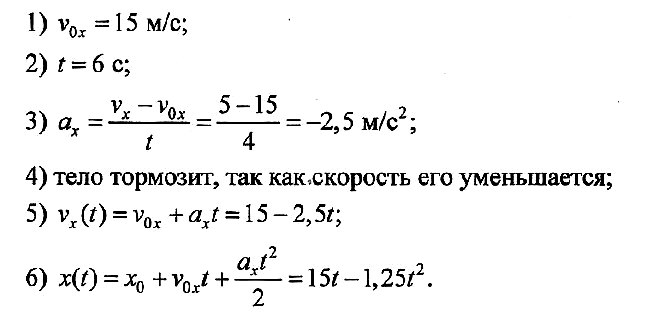S vx2 v0x2 2ax что это

Ускорение при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v ₀ — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость

Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.

Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.

Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения

v_x — проекция скорости тела в данный момент времени, v_0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость

Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:

При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.

Направление вектора ускорения

Направление вектора ускорения не всегда совпадает с направлением вектора скорости!

Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают ( а ↑↑ v ).

Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу ( а ↑↓ v ).

Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения

График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (a_x=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:

Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.

Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t₁ = 1 и t₂ = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).

Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Запишем исходные данные:

Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».

Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Внимательно прочитайте текст задани я и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела v_x от времени.

Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела a_x в интервале времени от 6 с до 10 с?

Алгоритм решения

Решение

Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.

Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:

Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:

Подставляем данные формулу и вычисляем модуль ускорения:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Скорость при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Описывая движение с постоянной скоростью, мы могли с уверенностью сказать, какую скорость имеет тело в любой момент времени. В случае с равноускоренным движением это не так, потому что скорость постоянно меняется. Поэтому для его описания вводится понятие мгновенной скорости.

Скорость тела в момент времени t равна сумме начальной скорости тела в момент времени t₀ и произведения ускорения этого тела на время t, в течение которого это тело двигалось. В векторном виде это записывается так:

v — скорость тела в данный момент времени, v ₀ —скорость тела в начальный момент времени, a — ускорение тела, t — время, в течение которого это тело двигалось

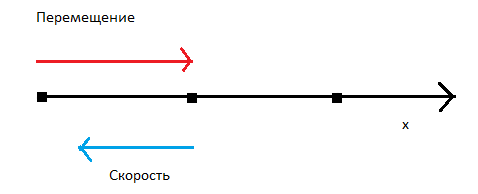
Направление вектора скорости при равномерном равноускоренном движении не всегда совпадает с направлением вектора ускорения и вектором перемещения тела.

Пример №1. Мальчик пробежал 200 метров по прямой линии, а затем вернулся в исходное положение. Определить направление вектора скорости и перемещения в момент, когда мальчик, возвращаясь в исходное положение, находился на полпути до него.

Началу вектора перемещения соответствует исходное положение мальчика. Когда мальчик возвращался и находился на полпути до исходного положения, концу вектора его перемещения соответствовала точка, лежащая посередине 200-метрового отрезка. Поэтому вектор перемещения направлен в сторону ОХ. Но мальчик в это время направлялся в обратную сторону. Поэтому его скорость была направлена против направления оси ОХ.

Скалярная формула скорости

В случае равноускоренного прямолинейного движения можно вместо векторов использовать скаляры. Тогда формула примет следующий вид:

Знак «+» ставится в случае, когда тело разгоняется, знак «–» — когда оно тормозит.

Проекция скорости

Проекция скорости при равноускоренном прямолинейном движении имеет вид:

Знак проекции скорости зависит от того, в какую сторону движется тело:

Знак проекции скорости не зависит от того, каким является движение: равнозамедленным или равноускоренным.

График скорости

График скорости — график зависимости проекции скорости от времени. Графиком скорости при равноускоренном прямолинейном движении является прямая.

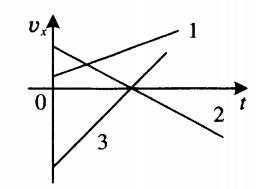
Сравнение модулей ускорения по графикам скоростей

Чтобы сравнить модули ускорений по графикам скоростей, нужно сравнить их углы наклона к оси времени. Чем больше между ними угол, тем больше модуль ускорения. Так, на рисунке выше большим модулем ускорения обладает тело 3 — угол между его графиком скорости и осью времени максимальный. Меньшим модулем ускорения обладает тело 1, так как угол между его графиком скорости и осью времени минимальный.

Пример №2. Ниже представлен график движения велосипедиста. Опишем характер его движения на участке от 0 до 2 с, в момент времени t=2 с и на участке от 2 с.

На отрезке пути от 0 до 2 с велосипедист двигался в направлении, противоположном оси ОХ. При этом модуль его скорости уменьшался. В момент времени t=2 c велосипедист приостановился и поменял направление движения, и дальше оно стало совпадать с осью ОХ. Модуль его скорости при этом начал расти. Но на всем пути независимо от направления движения велосипедиста вектор его ускорения всегда был направлен в сторону ОХ. Однако до 2 с движение считалось равнозамедленным, так как ускорение и скорость были направлены в противоположные стороны. После 2 с движение стало равноускоренным, так как направления скорости и ускорения совпали.

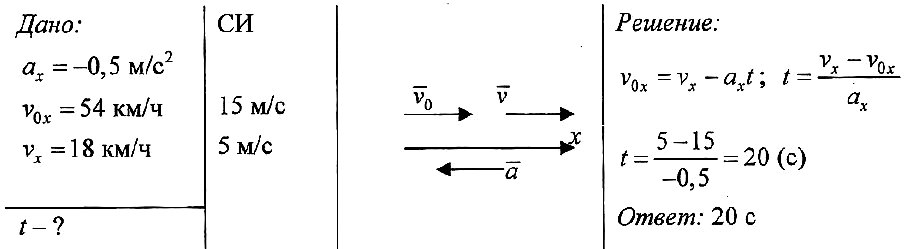
Пример №3. Грузовик ехал с некоторой постоянной скоростью. Затем он затормозил и остановился в течение 5 секунд. Найти постоянную скорость, с которой двигался грузовик, если при торможении модуль его ускорения составил 2 м/с.

Так как движение равнозамедленное, в формуле будем использовать» знак «–». Он будет указывать на то, что скорость грузовика с течением времени уменьшалась:

Выразим начальную скорость:

Так как грузовик в итоге остановился, его конечная скорость равна 0. Подставляем известные данные в формулу и получаем:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Источник

S vx2 v0x2 2ax что это

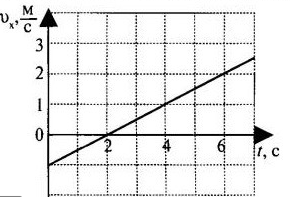
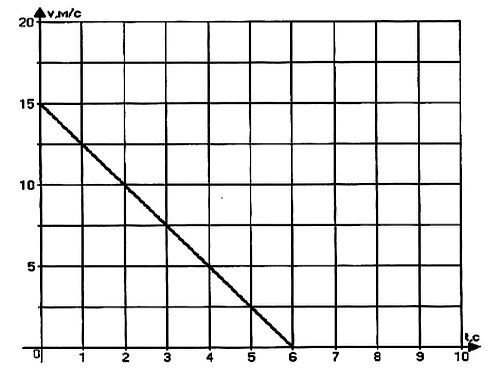
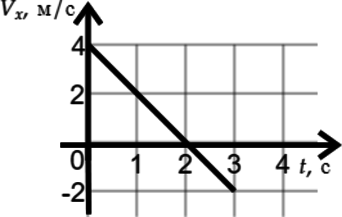
Задача № 3. По графику проекции скорости определите: 1) начальную скорость тела; 2) время движения тела до остановки; 3) ускорение тела; 4) вид движения (разгоняется тело или тормозит); 5) запишите уравнение проекции скорости; 6) запишите уравнение координаты (начальную координату считайте равной нулю).

Решение:

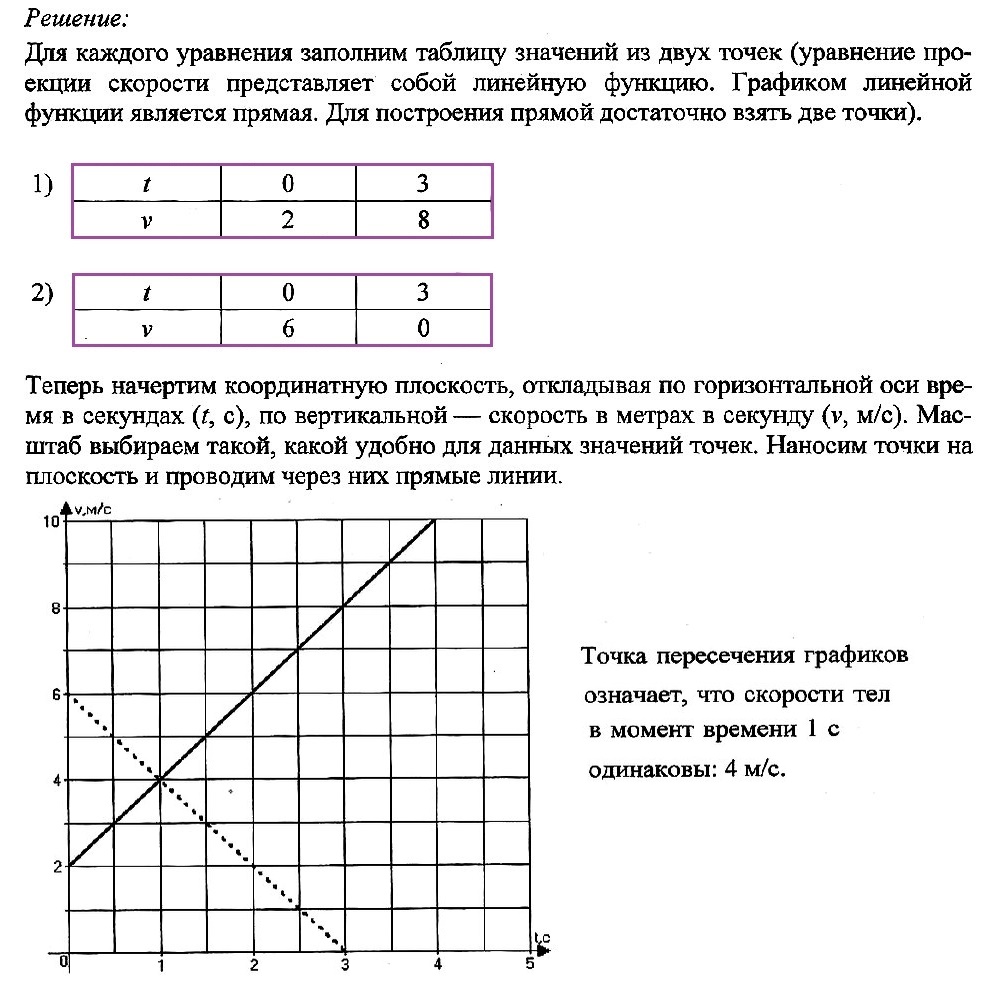
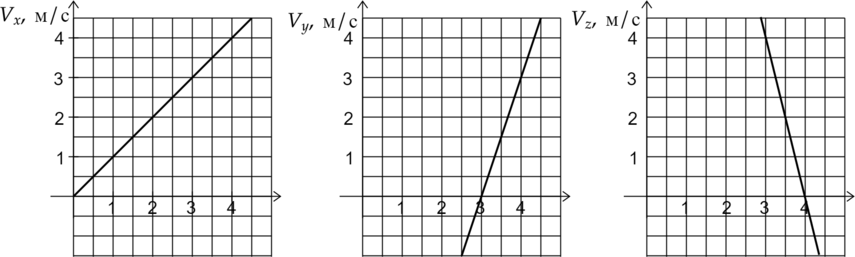
Задача № 4. Движение двух тел задано уравнениями проекции скорости:
v_1x(t) = 2 + 2t
v_2x(t) = 6 – 2t
В одной координатной плоскости постройте график проекции скорости каждого тела. Что означает точка пересечения графиков?

Решение:

Задача № 7. Самолет, летевший прямолинейно с постоянной скоростью 360 км/ч, стал двигаться с постоянным ускорением 9 м/с 2 в течение 10 с в том же направлении. Какой скорости достиг самолет и какое расстояние он пролетел за это время? Чему равна средняя скорость за время 10 с при ускоренном движении?

Краткое пояснение для решения
ЗАДАЧИ на Прямолинейное равноускоренное движение.

Равноускоренным движением называется такое движение, при котором тело за равные промежутки времени изменяет свою скорость на одну и ту же величину. Движение, при котором скорость равномерно уменьшается, тоже считают равноускоренным (иногда его называют равнозамедленным).

Величины, участвующие в описании равноускоренного движения, почти все векторные. При решении задач формулы записывают обычно через проекции векторов на координатные оси. Если тело движется по горизонтали, ось обозначают буквой х, если по вертикали — буквой у.

Если векторы скорости и ускорения сонаправлены (их проекции имеют одинаковые знаки), тело разгоняется, т. е. его скорость увеличивается. Если же векторы скорости и ускорения противоположно направлены, тело тормозит.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равноускоренное движение с решениями». Выберите дальнейшие действия:

29 Комментарии

Спасибо за альтернативную точку зрения, не указанную в школьных учебниках физики. Надеюсь, это поможет учащимся расширить свой кругозор в области физики.

Ускорение — это вектор, а он отрицательным быть не может. Но вот проекция ускорения очень даже может быть отрицательной. И, прямо скажем, я не пойму что Вы тут написали, но попахивает каким-то бредом. Хотя бы потому, что at — это приращение скорости, а средняя скорость — это перемещение деленное на время движения, или путь на время движения, если интересует средняя ПУТЕВАЯ скорость. Деление же на 2, в уравнении движения возникает из-за правил интегрирования, которые говорят о том, что интеграл at по dt равен 0.5at^2/

Тело движется прямолинейно под действием постоянной силы 12 Н, при этом зависимость координаты тела от времени имеет вид: (м). Определить: массу тела; импульс тела в момент времени t = 2 c ; среднюю скорость за промежуток времени от t1 = 0 c до t2 = 2 c.

S/tt=F/m. S=? Тело двигалось,или стояло?

….мощность мотора при условиях в задаче. (вес машины…1200 кг)
..машина имела ускорение 4 м/сс.. (для машины-«приличное» ускорение..) F/1200=4 сек.сек. F=4800 кг м./сек. Это=64 л.с. при 100% КПД
КПД ДВС=16 %. 64*6,25=400 л.с. (есть такие моторы. Правда, вес ТАКИХ машин 2,5-3 тонны…) Вот пример «теории и практики». А если вес машины …2650 кг., то мотор должен быть: 4*2650/75*6,25=883 л.с.

Определить тормозную путь,если известны начальная скорость 30 м/сек и замедление 6 м/сек2

V кон.=2at. 30=2*6*t. t=2,5 c. S=att. 6*2,5*2,5. S=37,5 м.

В последней задаче: t= V ср./ a. Vср.=15 м/с. t=15/6=2,5 секунды (быстрее свободного падения…) S=att. 6*2,5*2/5=37,5 м.

(…напутал в решении…)
При «ускорении» 19 м/сс, скорость через 30 сек. будет: Vкон.=2at. 2*19*30. V кон.=1140 м/с. (4104 км/час)

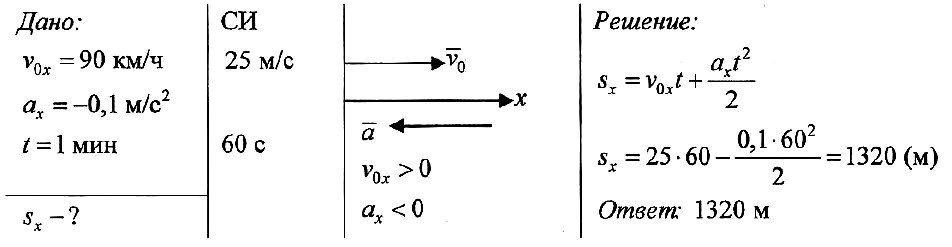
во второй задаче: V нач.=25 м/с. а=0,1 м/сс. t=60 c. S=? (давать надо одно: или «ускорение», или «время»)
решение: S=V ср.*t. 12,5*60=750 м. «ускорение»= V ср./t. 12,5/60. t=0,2 м/сс.
При «а»=0,1 м/сс. t=Vср./a. 12,5/0,1=125 секунд.
S при а=0,2 м/сс. S=att. 0,208*60*60=750 м. (и при разгоне, и при торможении)
S при а=0,1 м/сс. S=att. 0,1/125*125. S=1562,5 м. (и при разгоне. и при торможении)

задача № 9
V нач.=х. V кон.=5х. V ср.=3х. t=2c. S=18 м. V ср.=9 м. х=9/3=3 м/с. V кон.=15 м/с.
a=S/tt=Vср./t a=18/4=9/2=4,5 м/сс
ПРОВЕРКА: S=att. 4,5*2*2=18 м.
Проверка (по Вашему решению): a=6 м/сс. S=att/2. 6*2*2/2=12 м (?)

У Вас не получается, потому что Вы проверяете ответ по своей формуле. Правильная формула проекции перемещения указана в начале статьи и в самой задаче!

Вот такие «анонимы» в средневековье … всех, кто думал не так, как «принято». (текст изменен модератором сайта)

Во второй задаче некорректная формулировка. По факту, даны избыточные данные. «Тормозной путь» соответствует расстоянию до полной остановки, то есть такое понятие подразумевает конечную скорость, равную нулю. А по заданным числам конечная скорость будет равна v0 — a * t = 25 — 0.1*60 = 19 м/c.

Возможно, конкретно в это задаче автор подразумевал под тормозным путём участок, на котором поезд замедлял движение, при этом не до полной остановки. Меня это тоже вначале сбило с толку.

В 11-й задаче проще использовать формулу a = (V-Vo) / t

Даша! V конечная (при равно-ускоренном движении и одной из скоростей=0 ) есть 2at. СРЕДНЯЯ скорость (25+0)/2=12,5 м/с. С такой СРЕДНЕЙ скоростью поезд за минуту (60 сек) пройдёт: 12,5*60=750 м.
Если задачу решать через «а», то t=12,5/0,1=125 секунд. S=V ср.*t. 12,5*125=1562,5 м.
Если поезд (по условию задачи) прошёл 750 м. (до остановки), то его ЗАМЕДЛЕНИЕ скорости (-«а»): S=att 750/60/60. а=0,2 м/сс.
Вывод: давать в условии задачи одно: или «а», или t

С точки зрения физики торможение — это тоже ускорение, только с обратным знаком. Поменяли условие задачи № 2, чтобы не было двусмысленности.

всем доброго времени.
Очень е силен в физике последние лет 25, по этой причине прошу помочь в решении некой задачи!
Дано начальная скорость = 10 м/с.
Вопрос сможет ли тело долететь до высоты 4 м и если сможет то с какой скоростью. Да, полет вертикальный!
На мой взгляд в даны не все условия, но могу и ошибаться.
Спасибо.

Такие задачи рассматриваются в разделе «Задачи на свободное падение» https://uchitel.pro/задачи-на-свободное-падение/

Добавить комментарий Отменить ответ

Конспекты по физике:

7 класс

8 класс

9 класс

10-11 классы

Найти конспект:

О проекте

Сайт «УчительPRO» — некоммерческий школьный проект учеников, их родителей и учителей. Продолжая использовать наш сайт, вы даете согласие на обработку файлов cookie и других пользовательских данных в целях функционирования сайта, проведения статистических исследований и обзоров. Если вы не хотите, чтобы ваши данные обрабатывались, покиньте сайт.

Возрастная категория: 12+

(с) 2021 Учитель.PRO — Копирование информации с сайта только при указании активной ссылки на сайт!

Источник

Равноускоренное прямолинейное движение (страница 2)

Равноускоренное движение — это движение с постоянным вектором ускорения \(\displaystyle \vec =const.\)

Уравнение координаты материальной точки в проекциях на ось при равноускоренном движении: \[x=x_0+v_\text<0x>t+\dfrac<2>\] Формула для скорости при равноускоренном движении: \[v_x=>t+a_xt\]

Рыжий Боб бежит к миске с едой. На графике представлена зависимость проекции скорости кота \(\upsilon _x\) на ось \(Ox\) от времени. Какой путь был пройден Бобом за \(t=4\) с? (Ответ дайте в метрах.)

На протяжении всего интервала времени проекция скорости Боба на ось Ox положительна. Поэтому, для того чтобы найти путь, пройденный котом, необходимо вычислить площадь под графиком. К моменту времени \(t=4\) с кот прошел путь: \[S=\frac12\cdot2\cdot2+2\cdot2=6 \text< м>\]

На рисунке изображены графики зависимости модуля скорости движения четырех автомобилей от времени. Найдите путь тормозящего автомобиля за первые 15 с. (Ответ дайте в метрах.)

Для того чтобы по графику модуля скорости найти путь, пройденный автомобилем за некоторый интервал времени, необходимо вычислить площадь под частью графика, соответствующей этому интервалу времени. Из приведенного рисунка видно, что отрицательная проекция ускорения у третьего автомобиля, значит, он тормозит. Найдём его путь, используя формулу для площади трапеции: \[S=\frac<15+10><2>\cdot 15=187,5 \text< м>\]

Точечное тело движется вдоль оси Оx. В начальный момент времени тело находилось в точке с координатой \(x_0=-10\) м. На рисунке изображена зависимость проекции скорости этого тела от времени t. Чему равна координата этого тела в момент времени \(t=5\) с? (Ответ дайте в метрах.)

По графику видно, что движение тела — равноускоренное.
Начальная скорость \(v_0=2\) м/с, проекция ускорения: \[\displaystyle a_x=\frac><\Delta t>=\frac<6-2><2>=2 \text< м/с>^2\] Уравнение для координаты тела при равноускоренном движении: \[x=x_0+V_0t+\frac2=-10+2t+t^2\] При \(t=5\) координата этого тела равна: \[x=-10+2\cdot5+5^2=25 \text< м >\]

Точечное тело движется вдоль оси Оx. В начальный момент времени тело находилось в точке с координатой \(x_0=15\) м. На рисунке изображена зависимость проекции скорости этого тела от времени t. Чему равна координата этого тела в момент времени \(t=5\) с? (Ответ дайте в метрах.)

По графику видно, что движение тела — равноускоренное.
Начальная скорость \(v_0=4\) м/с, проекция ускорения: \[\displaystyle a_x=\frac><\Delta t>=\frac<-2-4><3>=-2 \text< м/с>^2\] Уравнение для координаты тела при равноускоренном движении: \[x=x_0+V_0t+\frac2=15+4t-t^2\] При \(t=5\) с координата этого тела равна: \[x=15+4\cdot5-5^2=10 \text< м >\]

Вектор скорости мотылька находится по формуле: \[\vec = \vec(t) + \vec(t) + \vec(t)\] В момент времени \(t = 3\) с \(V_x = 3\) м/с, \(V_y = 0\) м/с, a \(V_z = 4\) м/с. Так как проекция скорости на ось \(OY\) равна 0, то: \[\vec = \vec(t) + \vec(t)\] Так как оси перпендикулярны друг другу, то получаем прямоугольный треугольник. По теореме Пифагора: \[v^<2>(t) = V_x^<2>(t) + V_z^<2>(t)\] Отсюда выражаем \(v^<2>(t)\) : \[v(t) = \sqrt(t) + V_z^<2>(t)> = \sqrt <3^<2>+ 4^<2>> = 5 \text< м/с>\]

Мяч подброшен вертикально вверх. Через 2 с после броска его скорость стала равна 5 м/с. Какова начальная скорость мяча? Сопротивлением воздуха пренебречь. (Ответ дайте в метрах в секунду.)

По условию задачи, сопротивлением воздуха пренебрегаем, тогда на мяч действует только сила тяжести, она же и создает ускорение свободного падения, направленное против движения тела. Тогда скорость в момент времени \(t\) определяется по формуле: \[v(t) = v_ <0>— gt\]

Источник