шашки на python код

Как я шашки писал

Предыстория

Так уж получилось, что моим первым более-менее серьёзным проектом, связанным с программированием, была реализация шашек для «Шага в будущее». К несчастью, доделать его до конца у меня так и не получилось, так как через некоторое время концепция проекта резко поменялась. Несмотря на это, программа была практически готова и с ней даже можно было играть, к тому же сам процесс её написания оказался весьма интересным, поэтому я решил поделиться теми идеями и алгоритмами, которые сумел придумать.

Правила игры

Реализация

Сначала необходимо определить, как наша доска будет храниться в памяти. Оптимальным решением, на мой взгляд, является массив из 32 объектов, каждый из которых имеет набор методов и свойств. Свойства хранят всю возможную информацию о клетке, например:

Разумеется, это не все необходимые свойства, однако приводить все я не вижу смысла. Что касается методов, то их немного и они выполняют несложные действия типа изменения полей queen, color и прочих, а затем обновляют изображение. Так, при бое будут вызваны функции для «очищения» той клетки, с которой идёт бой и той клетки, на которой стоит срубленная шашка, а так же для отрисовки шашки на том поле, куда происходит бой.

Однако как же определять, нужно рубить, или нет? Для этого перед каждым ходом доска сканируется, проверяя выполнение нескольких условий, выполнение которых означает, что нужно бить. Но для того, чтобы это сделать, придется разбить доски на диагонали, так как бой происходит именно по ним (это, кстати, нужно и для обычных ходов).

Разбивка на диагонали происходит именно так. Обратите внимание, что все диагонали перечислены снизу-вверх. Это сделано для удобства программиста, хотя и не является обязательным. В свойствах объектов перечислены все эти диагонали, а у тех диагоналей, на которых клетка лежит, стоит true, на остальных — false.

Таким образом, я создал несколько массивов, каждый из которых содержал ссылки на объекты, соответствующие клеткам, которые находятся на диагонали, которой соответствует массив. Это позволяет нам заставить шашки двигаться.
Я не буду расписывать алгоритм до мелочей, опишу лишь в общих чертах: если на какой-либо из диагоналей встречается следующая ситуация:
«шашка(1) — шашка (2) — пустое поле» (где 1 и 2 — игроки и ход сейчас делает игрок №1), либо «пустое поле — шашка(2) — шашка (1)» [для боя в обе стороны], то присвоить свойству первой клетки, отвечающему за информацию о том, должна ли она рубить, единичку. Кроме этого присвоить некой общей переменной(назовем её jumpInd), отвечающей за бои, единичку. Это нужно, потому что может возникнуть ситуация, в которой у игрока будет выбор какой из шашек рубить.

Когда игрок нажимает на какую-либо шашку, первым делом проверяется условие jumpInd. Если jumpInd=1, а шашка, на которую кликнул игрок, не должна бить, то ничего не происходит, либо выводится сообщение о том, что игрок обязан рубить. Если jumpInd=0, то проверяется, может ли эта шашка сделать ход. Проверка выполняется аналогично проверке на бой, только немного короче: если на одной из диагоналей встречается ситуация: «шашка(1) — пустое поле(для белых) и пустое поле — шашка(1)» [для черных], то подсветить это поле. Если jumpInd=1 и игрок выбрал шашку, которой этот бой и будет производиться, то клетка, на которую будет произведен бой, также подсвечивается. Можно подсветить и шашку, которой будет сделан ход. Эти действия нужны лишь для удобства игрока. Следующим действием игрок может кликнуть по другой шашке и тогда алгоритм начнется сначала, а может кликнуть по подсвеченному полю и совершить таким образом ход.

После того, как игрок кликнул по подсвеченному полю, выполняются все методы, «подчищающие хвосты» и меняющие цвета клеток. Если jumpInd был равен нулю, то передаем ход второму игроку. Если jumpInd=1, то нужно проверить, может ли игрок срубить ещё что-либо. Если да, то подсветим поля, на которые он может попасть в результате боя. Не стоит забывать производить проверку того, не стала ли шашка дамкой. Если да, то бой будет производиться уже по дамочным правилам. Если боя вообще нет, то опять проверим на превращение в дамку, обнулим jumpInd и передадим ход.

Нам удалось реализовать простые передвижения шашки, но это только начало. Теперь мы должны реализовать движение дамок. Здесь всё несколько сложнее в реализации, по крайней мере я с ними изрядно попотел, хотя сама суть похожа.

Для каждой диагонали производится проверка условий в обе стороны, но я буду писать лишь в одну, потому что суть лишь в порядке проверок.
Проверка для хода: если встречается ситуация: «дамка — пустое поле», то подсветить эту клетку и проверить следующую. Выполнять до тех пор, пока диагональ не закончится, либо пока не встретится шашка(дамка) противоположного цвета.
Проверка для боя: если встречается ситуация: «дамка — z пустых полей — шашка(дамка) противоположного цвета — n пустых полей» (z>=0, n>0), то подсветить все n пустых полей после шашки соперника (если встретится ещё одна шашка противника, то прекратить) и проделать все те манипуляции с переменными, хранящими информацию о боях, что и в случае с обычной шашкой. После того, как игрок кликнет на подсвеченную клетку, следует проверить возможность ещё одного боя в любую сторону, кроме той, из которой мы пришли. Реализация всех этих проверок и условий заняла у меня много времени и места, но, возможно, я просто что-то упустил и можно было реализовать всё короче и красивее.

И ещё одна очень важная вещь: не стоит забывать о следующем условии: шашку нельзя срубить дважды. Это означает, что если шашка на диагонали, на которой вы сейчас находитесь, уже была срублена, то ход заканчивается (для обычной шашки на том поле, где она сейчас стоит, а для дамки на любым из пустых полей вплоть до этой уже срубленной шашки противника). Как вариант: можно хранить в каком-нибудь массиве адреса уже срубленных шашек, обнуляя его лишь при передаче хода. (собственно, я примерно так и делал)

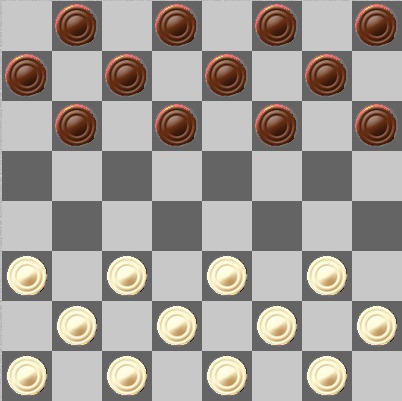
(Дамка черных обязана рубить следующим путём: h4:e1:c3:e5 и останавливаться, так как шашка g3 всё ещё на доске. После этого белые рубят в дамки и выигрывают)

Весь этот алгоритм можно очень кратко описать следующей блок-схемой:

Первый клик:

Второй клик:

Чтобы программа поняла, где первый клик, а где второй, — создадим логическую переменную, false = первый клик, true = второй клик.

В общем-то, на этом реализация правил игры заканчиваются. Всё выглядит относительно несложно, но при переносе алгоритма в код возникает множество мелких проблем и трудностей, из-за которых код всё разбухает и разбухает. Виноват в этом сам принцип реализации доски, выбранный мной, но это лучшее из того, что пришло в голову за те две-три недели (да и те с ощутимыми перерывами), так как все действия максимально наглядны, запутаться практически невозможно, а код читается достаточно легко. Полагаю, что пожертвовать ради этого лаконичностью кода — допустимо.

Искусственный Интеллект

Однако на этом наши приключения не заканчиваются. Замечательно, что мы научили шашки двигаться, но с кем же мы будем играть? Нам необходимо создать искусственный интеллект для игры. К сожалению, полноценно его реализовать у меня так и не получилось, так как из-за плохой оптимизации программа начинала виснуть при просчете далее, чем на 5-6 ходов (порядка 20-25 тысяч позиций). При реализации я пользовался книгой Программирование шахмат и других логических игр и рекомендую её всем, кто заинтересуется проблемой ИИ в логических играх. Я остановился на улучшенном алгоритме «альфа-бета отсечений», но описывать здесь я его не буду, потому что он уже много раз на Хабре был описан до меня, например:

К несчастью, концепция моего проекта на конкурс, как я уже говорил в начале, поменялась — поэтому ИИ так и остался недоделанным и был отброшен в дальний ящик. Некоторые принципы оценки позиции, которые я успел сформулировать — тоже. Я мог бы привести их здесь, но особого интереса из-за своей специфичности они не представляют. Если кому-то будет интересно, то могу написать отдельную статью про функцию оценки и алгоритм отсечений. Так как всё это дело происходило полгода назад и статью я писал в основном по памяти, то где-то могли возникнуть неточности или несоответствия, буду рад, если вы укажите мне на них в комментариях. Если что-то нужно расписать более подробно, то обращайтесь там же. Спасибо за внимание.

Источник

Шашки на python код

AI for Playing Russian Checkers (aka «Shashki»)

The code plays Russian Checkers (see official rules) against a popular Android App with the same name (500k+ installs, 4.3 stars). Below we refer to this app as the «Android app».

The original motivation of the project was to beat that app on the most difficult level (called «very hard»). This goal was achieved in that the present AI’s typically winning about 43% of the games while losing around 12% to the Android app; the remaining 45% are a draw. Please note that despite this specific goal the AI is not tied in any way to play against this specific app and it can be used to compute optimal moves using any API/front end.

At engine level there’s nothing fancy there. I had two goals in mind: i) gain in-depth understanding of how game tree search works and ii) create a solid and performant baseline for later experiments with Reinforcement Learning (RL). The code is fairly modular and the core parts are well tested, so please hack away, experiment, improve, or extend anything. And when done, don’t forget to send a PR!

Mostly for debugging and possibly of some pedagogical value, there’s the option to visualize and interactively explore the game tree in your browser for any given board.

The code was developed and tested on Ubuntu but it shouldn’t be hard to port it to MS Windows or macOS. At least there’s no platform-dependent hacks, promise!

Components and Folder Structure

The project contains a number of multiple, loosly coupled components:

The steps below assume that you’re on an Linux-based system. Adapting them for other platforms should be straightforward though.

Build and Run the Engine

Install CMake 3.9 or later

Build and install Pistache. We need it to run our REST service. When done edit CMakeLists.txt and have Pistache_DIR point to the install location

From the root directory, run

The build should complete without any errors or warnings

(optional) Now you may want to

Get Android Device Ready

Now we will fire up the Python client. It will control the Android app through ADB, retrieve the moves from the REST API and execute them.

Install the Android SDK. There’s at least two options:

Directly using the Play store of the Android device, you now want to fetch the Russian Checkers App app. Start a new game. It’s really important that you play white and run in «Tournament Mode» (use checkbox). This is a simplification from the driver code while the engine doesn’t mind what color you play

Setup a Python environment: the code has been run on Python 3.8.5 however it should work with any Python 3.5+. Typing

from the python sub-folder should to get you started the most important packages. Possibly you’ll manually have to add another package or two. Being this unspecific helps to reduce pollution in non-managed (i.e. non-conda-like) environments

Visualizing the Game Tree

Assuming the game server has been started as described above, you can visualize the game tree and explore it interactively simply by opening web/tree_viz/index.html in your browser of choice (tested on Chrome on Firefox). Just click the «Visualize» button.

Eventually you should see something similar to this (click to enlage):

As a reference, below’s the stats of a tournament where the AI (search depth 12) played 187 games against the Android app (at max difficulty). The AI significanlty outperformed the Android app, winning 81 games while the Android app won 23.

Conventions.

Board representation. The 8×8 chessboard contains 32 dark squares which mark the valid positions for any token. We index them as follows:

Each position may hold a man or a king while each of them can be black or white. Hence we choose a bitboard-type of representation of the board using two 64-bit integers (called a slice), one for black and one for white. Such a slice stores the positions of men in its lower 32 bits while king positions occupy the upper 32 bits.

Move representation. Similarly we represent a move with a single 16-bit integer by defining

where the five f and the five t bits each encode a number in 0..31, indicating the origin ( f

from) and the destination ( t

Actions. The above choice of representation is a trade-off between efficiency and usability. Despite highly optimized bitboard schemes exist, they are not straight-forward to apply to the Russian variant of checkers, mainly due to flying kings. Our representation allows for such moves while we can still express all operations using bitwise arithmetic.

Code Generation. We use Python to generate the code for four core functions,

Where To Go From Here

Given this reasonably strong baseline, it’ll be interesting to try out different RL techniques on this problem. As a start, you may want to write your own OpenAI Gym enviroment in Python and plug it into a framework/library such as tf_agents, Ray, or keras-rl. This should help to get a first impression on how far one can get with standard, discrete state space RL on this problem. Some inspiration may be found e.g. here.

Personally I’d expect this to work well since the problem is completely deterministic and most of the times the action space is manageable size. Only once kings start to show up on the board, the cardinality of the action space may require some extra thought.

Источник

Помогите пожалуйста решить! тренировочное задание по программированию : Шашки.

На доске стоит белая шашка. Требуется определить, может ли она попасть в заданную клетку, делая ходы по правилам и не пользуясь ходами дамки (т. е. не используя возможность перемещаться назад после превращения в дамку). Белые шашки могут ходить по клеткам одного цвета по диагонали вверх-влево или вверх-вправо. Ходов может быть несколько!

Доска имеет размер 8×8, вертикали и горизонтали нумеруются числами от 1 до 8 начиная с левого нижнего угла. Исходная и конечная клетки не совпадают.

Вводится клетка, где стоит шашка, а затем клетка, куда шашка должна попасть.

Каждая клетка описывается номером вертикали, а затем номером горизонтали. Под номером вертикали имеется в виду не номер по вертикали, а номер вертикальной линии считая слева направо. Аналогичная формулировка используется для номера горизонтали: нумерация идет снизу вверх. Например, клетка A2 кодируется как 1 2.

Выведите слово YES (заглавными буквами), если шашка может попасть из начальной клетки в указанную, и NO в противном случае.

тест 1
входные данные:
1
1
2
2
вывод программы:
YES

тест 2
входные данные:
1
1
8
7
вывод программы:
NO
пишут неправильное решение!
не пойму! что не так?!

Это условие и задача из курса программирования на Питон.

75/100Оценка: 75 из 100
Нет! Задание не пройдено
Сдача задачи
75/100Оценка: 75 из 100

результаты анализатора
Test 10
Wrong answer.

Источник

Встреча шашек

попытался написать к ней код, но работает неправильно

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Вложения, ожидающие проверки

Screenshot (25).png

Гомоку (аналог шашек), рандомное расположение шашек
Здравствуйте! Помогите, пожалуйста, переделать код так, чтобы шашки появлялись не по щелчку, а.

Проектироваение шашек
Доброго времени суток, форумчане. Задался целью написать шашки используя связку Qt, OpenGL, C++.

ИИ для шашек
помогите как найти коэффициенты для правильных ходов бота

Движение шашек
Не знаю даже с чего начать. Есть класс Block, в котором хранятся параметры одной шашки, т.е.

Комментарий администратора

Задание должно быть в виде текста, а не картинки.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Алгоритм шашек
Возникла идея создать игру шашки комп. против человека. Конечно необходим алгоритм для компьютера.

Движение шашек
Игра происходит на прямоугольной площадке, разделённой на поля. Число полей должно быть нечётным и.

Встреча в реале.
А не напиться ли нам в реале по поводу нашего сосуществования и грядущего лета года сего две тысячи.

Нужен исходник шашек
Народ помогите, есть у кого исходники шашек на C#! P.S:Windows Form

Ищу исходники шашек
Пожалуйста, помогите мне написать шашки на Qt

Задача о стопке шашек
Здравствуйте, форумчане! На днях попалась следующая задача: на доске имеется пять ячеек (A, B, C.

Источник

Простые игры для кодирования на Python

Сегодня мы научимся кодировать несколько простых игр, используя распространенные модули Python.

Сегодня мы научимся кодировать несколько простых игр, используя распространенные модули Python.

Почему мы используем Python?

Python – это известный язык программирования. Python код очень легко понять и написать. Считается, что он удобен для разработчиков. Любой новичок может научиться кодировать на Python в течение короткого промежутка времени.

Вот некоторые из самых интересных особенностей этого языка:

Создание простых игр в Python

Давайте теперь реализуем несколько простых игр в Python, которые вы можете построить как новичок, чтобы начать свой путь обучения!

1. Игра викторина в Python

Это очень простая текстовая игра на Python. Это маленькая викторина, которую вы можете сделать для себя или своих друзей. Нам не нужно импортировать какие-либо модули для этой игры, что облегчает её! Попробуйте сами.

2. Игра в Pong на Python

Большинство из нас слышали о знаменитой игре в Pong. Многие из нас любят играть. Сегодня мы научимся кодировать эту классическую игру с помощью языка программирования python!

Прежде чем начать кодировать, необходимо установить модуль turtle. Этот модуль представляет собой библиотеку Python, которая позволяет пользователям создавать картины и фигуры, предоставляя им виртуальный холст.

Если у вас его еще нет, вы можете установить библиотеку, используя pip.

Вы можете узнать больше о библиотеке turtle из их официальной документации

Попробуйте код самостоятельно!

3. Игра Hungry Snake на Python

Это была наша любимая игра, когда мы были детьми. На самом деле мы можем реализовать эту игру в python, импортируя всего два модуля! Как это круто!

Во-первых, нам нужно установить библиотеку turtle. Если у вас она еще не установлена, откройте свой cmd и введите следующую команду.

Теперь мы установим случайное модуль. Случайный модуль используется для генерации случайных чисел. В вашем типе CMD в следующей команде.

Теперь мы установим модуль random2. Модуль random2 используется для генерации случайных чисел. Выполните в cmd следующую команду.

Попробуйте сами код ниже и наслаждайтесь игрой!

Заключение

Вот и все! Это некоторые из простых игр в Python, которые вы можете создать как новичок и повеселиться! Мы любили создавать эти игры, и мы надеемся, что у вас тоже получиться!

Источник