Sin альфа равен чему равен альфа

Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы

Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.

Синус, косинус, тангенс и котангенс. Определения

Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.

Определения тригонометрических функций

Данные определения даны для острого угла прямоугольного треугольника!

В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.

Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.

Угол поворота

В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.

Синус (sin) угла поворота

При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.

Числа

Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?

Синус, косинус, тангенс, котангенс числа

Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.

Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.

Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.

Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.

Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.

Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.

Тригонометрические функции углового и числового аргумента

Основные функции тригонометрии

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии

Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.

В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.

sin α = A 1 H O A 1 = y 1 = y

Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.

Источник

Тригонометрические формулы. Их вывод

Наиболее часто встречающиеся тригонометрические формулы:

\(\blacktriangleright\) Основные тождества: \[\begin <|l|l|>\hline \sin^2 \alpha+\cos^2 \alpha =1& \mathrm\, \alpha \cdot \mathrm\, \alpha =1 \\ &(\sin\alpha\ne 0, \cos\alpha\ne 0)\\[0.5ex] \hline &\\ \mathrm\, \alpha=\dfrac<\sin \alpha> <\cos \alpha>&\mathrm\, \alpha =\dfrac<\cos \alpha> <\sin \alpha>\\&\\ 1+\mathrm^2\, \alpha =\dfrac1 <\cos^2 \alpha>& 1+\mathrm^2\, \alpha=\dfrac1<\sin^2 \alpha>\\&\\ (\cos\alpha\ne 0)& (\sin\alpha\ne 0) \\ \hline \end\]

\(\blacktriangleright\) Формулы сложения углов: \[\begin <|l|r|>\hline &\\ \sin<(\alpha\pm \beta)>=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha & \cos<(\alpha\pm \beta)>=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &\\ \hline &\\ \mathrm\, (\alpha\pm \beta)=\dfrac<\mathrm\, \alpha\pm \mathrm\, \beta><1 \mp \mathrm\, \alpha\cdot \mathrm\, \beta> & \mathrm\, (\alpha\pm\beta)=-\dfrac<1\mp \mathrm\, \alpha\cdot \mathrm\, \beta><\mathrm\, \alpha\pm \mathrm\, \beta>\\&\\ \cos\alpha\cos\beta\ne 0&\sin\alpha\sin\beta\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формулы понижения степени: \[\begin <|lc|cr|>\hline &&&\\ \sin^2\alpha=\dfrac<1-\cos<2\alpha>>2 &&& \cos^2\alpha=\dfrac<1+\cos<2\alpha>>2\\&&&\\ \hline \end\]

\(\blacktriangleright\) Формулы произведения функций: \[\begin <|c|>\hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>-\cos<(\alpha+\beta)>\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos<(\alpha-\beta)>+\cos<(\alpha+\beta)>\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin<(\alpha-\beta)>+\sin<(\alpha+\beta)>\bigg)\\\\ \hline \end\]

\(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin <|l|r|>\hline &\\ \sin<2\alpha>=\dfrac<2\mathrm\, \alpha><1+\mathrm^2\, \alpha> & \cos<2\alpha>=\dfrac<1-\mathrm^2\, \alpha><1+\mathrm^2\, \alpha>\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end\]

\(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin <|c|>\hline \text<Частный случай>\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin<\left(\alpha\pm \dfrac<\pi>4\right)>\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin<\left(\alpha\pm \dfrac<\pi>6\right)>\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin<\left(x\pm \dfrac<\pi>3\right)>\\\\ \hline \text<Общий случай>\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt\cdot \sin<(\alpha\pm \phi)>, \ \ \cos\phi=\dfrac a<\sqrt>, \ \sin\phi=\dfrac b<\sqrt>\\\\ \hline \end\]

Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.

Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.

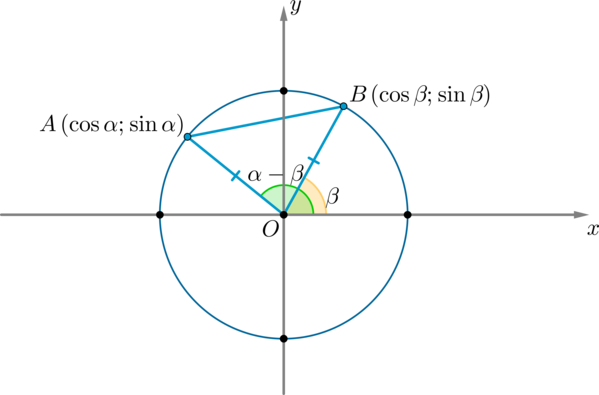
\(AB^2=AO^2+BO^2-2AO\cdot BO\cdot \cos(\alpha-\beta)=1+1-2\cos(\alpha-\beta) \ (1)\) (т.к. \(AO=BO=R\) – радиус окружности)

По формуле расстояния между двумя точками на плоскости:

Таким образом, сравнивая равенства \((1)\) и \((2)\) :

Отсюда и получается наша формула.

\(\blacktriangleright\) Вывод остальных формул суммы/разности углов:

Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения \(\sin x=\cos(90^\circ-x)\) и \(\cos x=\sin (90^\circ-x)\) :

\(\blacktriangleright\) Вывод формул двойного и тройного углов:

Данные формулы выводятся с помощью предыдущих формул:

1) \(\sin 2\alpha=\sin(\alpha+\alpha)=\sin\alpha\cos\alpha+\sin\alpha\cos\alpha=2\sin\alpha\cos\alpha\)

разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0 \Rightarrow \mathrm\,2\alpha=0\) ):

5) \(\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sin\alpha(1-2\sin^2\alpha)+\cos\alpha\cdot 2\sin\alpha\cos\alpha=\)

6) Аналогично выводится, что \(\cos3\alpha=\cos(\alpha+2\alpha)=4\cos^3\alpha-3\cos\alpha\)

\(\blacktriangleright\) Вывод формул понижения степени:

Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:

1) \(\cos2\alpha=2\cos^2\alpha-1 \Rightarrow \cos^2\alpha=\dfrac<1+\cos2\alpha>2\)

2) \(\cos2\alpha=1-2\sin^2\alpha \Rightarrow \sin^2\alpha=\dfrac<1-\cos2\alpha>2\)

\(\blacktriangleright\) Вывод формул произведения функций:

1) Сложим формулы косинуса суммы и косинуса разности двух углов:

Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)

2) Если вычесть из формулы косинуса суммы косинус разности, то получим:

3) Сложим формулы синуса суммы и синуса разности двух углов:

\(\blacktriangleright\) Вывод формул суммы/разности функций:

Получили формулу суммы косинусов.

Получили формулу разности косинусов.

Получили формулу суммы синусов.

4) Формулу разности синусов можно вывести из формулы суммы синусов:

Аналогично выводится формула суммы котангенсов.

\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:

(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\) ):)

\(\blacktriangleright\) Вывод формул вспомогательного угла:

Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.

\(a\sin x+b\cos x=\sqrt\left(\dfrac a<\sqrt>\sin x+ \dfrac b<\sqrt>\cos x \right)=\sqrt\big(a_1\sin x+b_1\cos x\big)\)

\(\sqrt\,\big(\cos \phi \sin x+\sin \phi\cos x\big)=\sqrt\,\sin (x+\phi)\) (по формуле синуса суммы двух углов)

Значит, формула выглядит следующим образом: \[<\large\,\sin (x+\phi),>> \quad \text <где >\cos \phi=\dfrac a<\sqrt>\] Заметим, что мы могли бы, например, принять за \(\cos \phi=b_1, \ \sin \phi=a_1\) и тогда формула выглядела бы как \[a\sin x+b\cos x=\sqrt\,\cos (x-\phi)\]

\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:

\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1<\sqrt2>\sin x\pm\dfrac1<\sqrt2>\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac<\pi>4\right)\)

\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac<\sqrt3>2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac<\pi>6\right)\)

\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac<\sqrt3>2\cos x\right)=2\,\sin\left(x\pm\dfrac<\pi>3\right)\)

Источник

Формулы приведения тригонометрических функций

Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.

Формулы приведения: список и таблицы

Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство.

Сначала запишем все формулы приведения:

Для угла (`\frac <\pi>2 \pm \alpha`) или (`90^\circ \pm \alpha`):

`sin(\frac <\pi>2 — \alpha)=cos \ \alpha;` ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha`
`cos(\frac <\pi>2 — \alpha)=sin \ \alpha;` ` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`
`tg(\frac <\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <\pi>2 + \alpha)=-tg \ \alpha`

Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):

`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`

Для угла (`\frac <3\pi>2 \pm \alpha`) или (`270^\circ \pm \alpha`):

`sin(\frac <3\pi>2 — \alpha)=-cos \ \alpha;` ` sin(\frac <3\pi>2 + \alpha)=-cos \ \alpha`
`cos(\frac <3\pi>2 — \alpha)=-sin \ \alpha;` ` cos(\frac <3\pi>2 + \alpha)=sin \ \alpha`
`tg(\frac <3\pi>2 — \alpha)=ctg \ \alpha;` ` tg(\frac <3\pi>2 + \alpha)=-ctg \ \alpha`
`ctg(\frac <3\pi>2 — \alpha)=tg \ \alpha;` ` ctg(\frac <3\pi>2 + \alpha)=-tg \ \alpha`

Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):

`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`

Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:

Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.

И вторая, аналогичная таблица, где углы записаны в градусах:

Мнемоническое правило формул приведения или как их запомнить

Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.

Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.Само привило содержит 3 этапа:

Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:

Ответ: ` cos(\pi + \alpha)= — cos \alpha`

2. `sin(\frac <3\pi>2 — \alpha)`.

Ответ: `sin(\frac <3\pi>2 — \alpha)= — cos \alpha`

3. `cos(\frac <7\pi>2 — \alpha)`.

`cos(\frac <7\pi>2 — \alpha)=cos(\frac <6\pi>2+\frac <\pi>2-\alpha)=cos (3\pi+(\frac<\pi>2-\alpha))`. Представим `3\pi` как `2\pi+\pi`. `2\pi` — период функции.

Важно: Функции `cos \alpha` и `sin \alpha` имеют период `2\pi` или `360^\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.

Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac<\pi>2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac<\pi>2-\alpha)= — cos (\frac<\pi>2-\alpha)= — sin \alpha`.

Ответ: `cos(\frac <7\pi>2 — \alpha)=- sin \alpha`.

Лошадиное правило

Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?

Итак, мы имеем функции с аргументами `\frac <\pi>2 \pm \alpha`, `\pi \pm \alpha`, `\frac <3\pi>2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac <\pi>2`, `\pi`, `\frac <3\pi>2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac <\pi>2` и `\frac <3\pi>2` на вертикальной оси ординат.

Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.

То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂

Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.

Практические примеры использования формул приведения

Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:

Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.

Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;

б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac<\sqrt 3>3`;

в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac<\sqrt 3>2`;

г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac<\sqrt 3>2`.

Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac <9\pi>8` и `cos \frac <9\pi>8`; 2) `sin \frac <\pi>8` и `cos \frac <3\pi>10`.

Решение: 1)`sin \frac <9\pi>8=sin (\pi+\frac <\pi>8)=-sin \frac <\pi>8`

`cos \frac <9\pi>8=cos (\pi+\frac <\pi>8)=-cos \frac <\pi>8=-sin \frac <3\pi>8`

2) `cos \frac <3\pi>10=cos (\frac <\pi>2-\frac <\pi>5)=sin \frac <\pi>5`

`sin \frac <\pi>8 Доказательство формул приведения

Докажем сначала две формулы для синуса и косинуса аргумента `\frac <\pi>2 + \alpha`: ` sin(\frac <\pi>2 + \alpha)=cos \ \alpha` и` cos(\frac <\pi>2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.

Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac <\pi>2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac <\pi>2 + \alpha)=x`, ` cos(\frac <\pi>2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac <\pi>2 + \alpha)=cos \alpha` и ` cos(\frac <\pi>2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac <\pi>2 + \alpha`.

Выходя из определения тангенса и котангенса, получим ` tg(\frac <\pi>2 + \alpha)=\frac 2 + \alpha)>2 + \alpha)>=\frac <-sin \alpha>=-ctg \alpha` и ` сtg(\frac <\pi>2 + \alpha)=\frac 2 + \alpha)>2 + \alpha)>=\frac <-sin \alpha>=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac <\pi>2 + \alpha`.

Чтобы доказать формулы с аргументом `\frac <\pi>2 — \alpha`, достаточно представить его, как `\frac <\pi>2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac <\pi>2 — \alpha)=cos(\frac <\pi>2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.

Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac <\pi>2 +(\frac <\pi>2+\alpha)` и `\frac <\pi>2 +(\frac <\pi>2-\alpha)` соответственно.

А `\frac <3\pi>2 + \alpha` и `\frac <3\pi>2 — \alpha` как `\pi +(\frac <\pi>2+\alpha)` и `\pi +(\frac <\pi>2-\alpha)`.

Источник