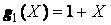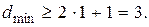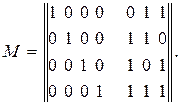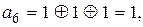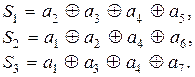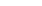систематические коды несистематические коды

Систематические коды несистематические коды

Евразийский национальный университет им. Л.Н. Гумилева, г. Астана

систематические и несистематические сверточные коды и распространение катастрофических ошибок

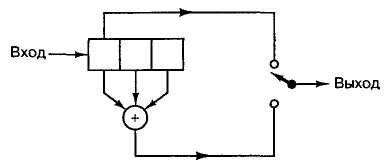
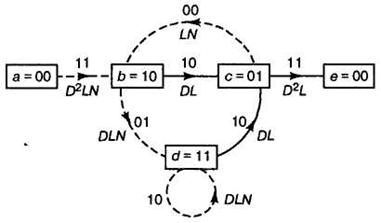
Рисунок 1 – Систематический сверточный кодер степенью

кодирования 1/2 и длиной кодового ограничения K = 3

Любой несистематический код, для линейных блочных кодов, можно преобра­ зовать в систематический с такими же пространственными характеристиками блоков. При использовании сверточных кодов это преобразование невозможно. Причина в том, что сверточные ко­ ды сильно зависят от просвета [1, 2, 3].

При построении сверточного кода в систематической форме при данной длине кодового ограничения и степени кодирования максимально возможное значение просвета снижается.

В таблице 1 показан максимальный просвет для сис­тематического и несистематического кодов при степени кодирования с K от 2 до 8. При большой длине кодо­вого ограничения результаты отличаются еще сильнее [ 4 ].

Сравнение систематического и несистематического просветов,

степень кодирования 1/2

Длина кодового ограничения

Просвет несистематического кода

Распространение катастрофических ошибок в сверточных кодах

(1)

Следовательно, в кодере, (рисунок 2 а ), может происходить распростра­ нение катастрофической ошибки.

Рисунок 2 – Кодер, в котором возможно накоп ление

катастрофической ошибки: а) кодер; б) диаграмма состояний

Поэтому, например, для канала BSC (двоичный симметричный канал) к выбору этого непра­ вильного пути могут привести три канальные ошибки. На таком пути может появить ся сколь угодно большое число ошибок (две плюс количество обхода петли). Для кодов со степенью кодирования 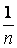можно видеть, что если каждый сумматор в кодере имеет четное количество соединений, петли, которые соответствуют информа­ционным состояниям со всеми единицами, будут иметь нулевой вес, отсюда следует, что код будет катастрофическим.

Единственное преимущество описанного ранее систематического кода заключается в том, что он никогда не будет катастрофическим, т.к. каждая петля должна содержать, по крайней мере, одну ветвь, порождаемую ненулевым входным битом. Следова­тельно, каждая петля должна содержать ненулевой кодовый символ.

Границы рабочих характеристик сверточных кодов

С помощью передаточной функции кода можно получить более подробную ин формацию, чем при использовании лишь расстояния между различными путями. В каждую ветвь диаграммы состояний введем множитель L так, чтобы этот показатель L мог служить счетчиком ветвей в любом пути из состояния a = 00 в состояние e = 00.

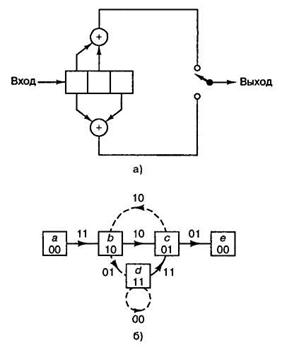
Введем также множитель N во все ветви переходов, порожденных входной двоичной единицей. Таким образом, после прохождения ветви суммарный множитель N возрастает на единицу, если только этот переход ветви вызван входной битовой единицей. Для сверточного кода, (рисунок 1), на перестроенной диаграмме состояний (рисунок 3) показаны дополнительные множители L и N.

Рисунок 3 – Диаграмма состояний с обозначением расстояния,

длины и числа входных единиц

Уравнения состоя­ ния вычисляются следующим образом:

(2)

Тогда передаточная функция кода такой доработанной диаграммы состояний будет иметь следующий вид [1, 2 ]:

(3)

Вероятность битовой ошибки P_b в бинарном сверточном ко­ де, использующем при декодировании жесткую схему принятия решений, может быть ограничена сверху следующим образом [ 5 ] :

Объединяя уравнения (5) и (6), запишем следующее:

При когерентной модуляции BPSK в канале с аддитивным белым гауссовым шумом ( AWGN ) вероятность битовой ошибки ограничивается следующей величиной:

– отношение энергии информационного бита к спектральной плотности мощности шума,

– отношение энергии канального символа к спектральной плотности мощности шума,

– степень кодирования,

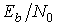
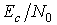
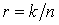
Q ( x ) – гауссов интеграл ошибок и определяется уравнением 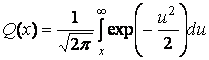и приведен в [ 1, таблица Б.1 ]. Следователь­но, для кода со степенью кодирования 1/2 и просветом d_f = 5, при использовании когерентной схемы BPSK и жесткой схемы принятия решений при декодировании, мо­ жно записать следующее:

1. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е, испр.: Пер. с англ. – Издательский дом «Вильямс», 2004. – 1104 с. ил.

2. Вернер М. Основы кодирования. Москва: Техносфера, 2004. – 288 с.

3. Ташатов Н.Н. Представление сверточного кодера. // в печати.

Источник

Систематические коды

Систематическими кодами называются блочные (n, k) коды, у которых k (обычно первые) разряды представляют собой двоичный неизбыточный код, а последующие r–контрольные разряды сформированы путем линейных комбинаций над информационными.

Основное свойство систематических кодов: сумма по модулю два двух и более разрешенных кодовых комбинаций также дает разрешенную кодовую комбинацию.

Правило формирования кода обычно выбирают так, чтобы при декодировании имелась возможность выполнить ряд проверок на четность для некоторых определенным образом выбранных подмножеств информационных и контрольных символов каждой кодовой комбинации. Анализируя результаты проверок, можно обнаружить или исправить ошибку ожидаемого вида.

Информацию о способе построения такого кода содержит проверочная матрица, которая составляется на базе образующей матрицы.

Образующая матрица М состоит из единичной матрицы размерностью k×k и приписанной к ней справа матрицы дополнений размерностью k×r:

(12.11)

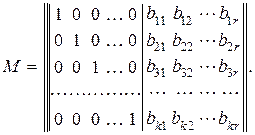
Размерность матрицы дополнений выбирается из выражения (12.8) или (12.9). Причем вес w (число ненулевых элементов) каждой строки матрицы дополнений должен быть не меньше, чем d_min – 1.

Проверочная матрица N строится из образующей матрицы следующим образом. Строками проверочной матрицы являются столбцы матрицы дополнений образующей матрицы. К полученной матрице дописывается справа единичная матрица размерностью r×r. Таким образом, проверочная матрица размерностью r×k имеет вид:

(12.12)

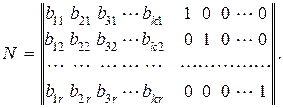
Единицы, стоящие в каждой строке, однозначно определяют, какие символы должны участвовать в определении значения контрольного разряда. Причем единицы в единичной матрице определяют номера контрольных разрядов.

Пример 12.1. Получить алгоритм кодирования в систематическом коде всех четырехразрядных кодовых комбинаций, позволяющий исправлять единичную ошибку. Таким образом, задано число информационных символов k = 4 и кратность исправлений S = 1. По выражению (12.9) определим число контрольных символов:

.

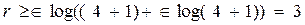
Минимальное кодовое расстояние определим из выражения (12.6):

Строим образующую матрицу:

Проверочная матрица будет иметь вид

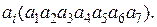
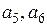
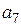
Обозначим символы, стоящие в каждой строке, через Символы и примем за контрольные, так как они будут входить только в одну из проверок.

Составим проверки для каждого контрольного символа. Из первой строки имеем

(12.13)

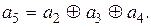
Из второй строки получим алгоритм для формирования контрольного символа a₆:

(12.14)

Аналогично из третьей строки получим алгоритм для формирования контрольного символа :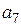

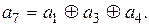
(12.15)

Нетрудно убедиться, что все результаты проверок на четность по выражениям (12.13)–(12.15) дают нуль, что свидетельствует о правильноcти составления образующей и проверочной матриц.

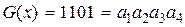
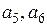
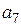
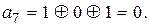
Пример 12.2. На основании алгоритма, полученного в примере 12.3, закодировать кодовую комбинацию в систематическом коде, позволяющим исправлять одиночную ошибку. По выражениям (12.13), (12.14) и (12.15) найдем значения для контрольных символов и :

(12.16)

Таким образом, кодовая комбинация F(X) (10.16) в систематическом коде будет иметь вид

На приемной стороне производятся проверки Si принятой кодовой комбинации, которые составляются на основании выражений (12.13), (12.14) и (12.15):

Если синдром (результат проверок на четность) S₁S₂S₃ будет нулевого порядка, то искажений в принятой кодовой комбинации F’(X) нет. При наличии искажений синдром S₁S₂S₃ указывает на искаженный символ.

0 0 0 – искажений нет,

1 0 0 – искажен символ а₅,

0 1 0 – искажен символ а₆,

0 0 1 – искажен символ а₇,

1 1 0 – искажен символ а₂,

0 1 1 – искажен символ а₁,

1 1 1 – искажен символ а₄,

1 0 1 – искажен символ а₃. (12.19)

Пример 12.3. Кодовая комбинация F(X) = 1 1 0 1 0 1 0 (пример 12.2) при передаче была искажена и приняла вид F′(X) = 1 1 1 1 0 1 0 = а₁ а₂ а₃ а₄ а₅ а₆ а₇. Декодировать принятую кодовую комбинацию.

Произведем проверки согласно выражениям (10.18):

,

,

.

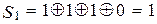
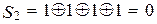
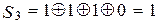
Полученный синдром S₁S₂S₃ = 101 согласно (10.19) свидетельствует об искажении символа а₃. Заменяем этот символ на противоположный и получаем исправленную кодовую комбинацию F(X) = 1 1 0 1 0 1 0, а исходная кодовая комбинация имеет G(X) = 1 1 0 1, что совпадает с кодовой комбинацией, подлежащей кодированию в примере 12.2.

Рекуррентные коды

Эти коды относятся к непрерывным кодам, в которых операции кодирования и декодирования производятся непрерывно над последовательностью информационных символов без деления на блоки. Рекуррентные коды применяются для обнаружения и исправления пакетов ошибок. В данном коде после каждого информационного элемента следует проверочный элемент. Проверочные элементы формируются путем сложения по модулю два двух информационных элементов, отстоящих друг от друга на шаг сложения, равный b.

Рассмотрим процесс кодирования на примере кодовой комбинации, приведенный на рис. 12.4 (верхняя строка), если шаг сложения b = 2. Процесс образования контрольных символов показан на этом же рисунке (нижняя строка).

Кодирование производимое кодером, схема которого приведена на рис. 12.5. Как видно из рисунка 12.6 входные символы задерживаются на 2b тактов, что эквивалентно дописыванию 2b нулей перед входной кодовой комбинацией (рис. 12.4).

Рис. 12.4. Схема построения рекуррентного кода

Кодирование и декодирование производятся с помощью регистров сдвига и сумматоров по модулю два.

На выходе кодирующего устройства (рис. 12.5) получим последовательность символов

Эта последовательность поступает в дискретный канал связи.

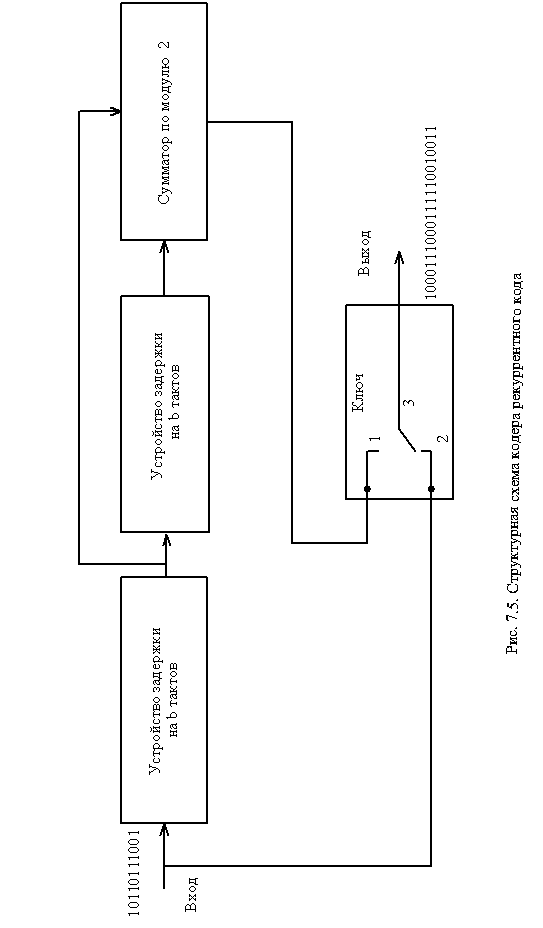
Структурная схема декодера приведена на рис. 12.6.

Процесс декодирования заключается в выработке контрольных символов из информационных, поступивших на декодер, и их сравнении с контрольными символами, пришедшими из канала связи. В результате сравнения вырабатывается корректирующая последовательность, которая и производит исправление информационной последовательности.

Рассмотрим этот процесс более подробно. Пусть из дискретного канала связи на вход подается искаженная помехами последовательность (искаженные символы обозначены сверху чертой)

(12.21)

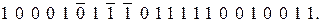
Устройство разделения (рис. 12.4) разделяет последовательность (12.21) на информационные последовательности:

(12.22)

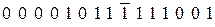
и контрольные символы:

. (12.23)

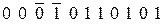
Последовательности символов (12.22) и (12.23) содержат ошибочные символы, которые подчеркнуты сверху. Формирователь контрольных символов из (10.22), по тем же правилам, что и при кодировании входной комбинации, выдает последовательность символов

0 0 1 0 0 1 0 0 0 0 1, (12.24)

которая в сумме по модулю два с последовательностью (10.23) дает исправляющую последовательность

0 0 1 1 0 0 1 0 1 0 0. (12.25)

Исправляющая последовательность (12.25) подается на инвертор, который выдает последовательность (12.26) и одновременно поступает на устройство задержки на b и 2b тактов. На выходе устройств задержки появляются последовательности (12.27) и (12.28) соответственно. На выходе схемы совпадения получаем последовательность (10.29)

Точки в последовательностях слева обозначают задержку символов на соответствующее число тактов. Единица на выходе схемы совпадения возникает только в тех случаях, когда на все его три входа подаются единицы. Она представляет собой команду исправить ошибку. Исправленная последовательность вырабатывается устройством коррекции в виде суммы по модулю два последовательности (12.29) и (12.22), задержанной на b тактов:

. (12.30)

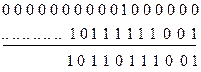
Точки в последовательности слева означают задержку на шесть тактов относительно входа в устройство разделения на информационные и контрольные символы.

После автоматического исправления последовательность (12.30) совпадает с последовательностью на рис. 12.4 (верхняя строка). Как следует из (12.29), на пути информационных символов включено 3b = 6 ячеек регистра сдвига. При этом для вывода всех ошибочных символов необходим защитный интервал 6b + 1 = 13 символов.

Рассмотренный код позволяет исправлять пакет ошибок длиной l = 2b = 4.

В заключение следует отметить, что рекуррентный код находит применение в системах связи, для передачи факсимильных сообщений.

Сверточные коды

Методы кодирования и декодирования, рассмотренные в подразделе 12.5, относились к блочным кодам. При использовании таких кодов информационная последовательность разбивается на отдельные блоки, которые кодируются независимо друг от друга. Таким образом, закодированная последовательность становится последовательностью независимых слов одинаковой длины.

При использовании сверточных кодов поток данных разбивается на гораздо меньшие блоки длиной k символов (в частном случае k₀ = 1), которые называются кадрами информационных символов.

Кадры информационных символов кодируются кадрами кодовых символов длиной n₀ символов. При этом кодирование кадра информационных символов в кадр кодового слова производится с учетом предшествующих m кадров информационных символов. Процедура кодирования, таким образом, связывает между собой последовательные кадры кодовых слов. Передаваемая последовательность становится одним полубесконечным кодовым словом.

Основными характеристиками сверточных кодов являются величины:

– k₀ – размер кадра информационных символов;

— n₀ – размер кадра кодовых символов;

— m – длина памяти кода;

— k = (m+1) × k₀ – информационная длина слова;

— n = (m+1) × n₀ – кодовая длина блока.

Кодовая длина блока – это длина кодовой последовательности, на которой сохраняется влияние одного кадра информационных символов.

Наконец, сверточный код имеет еще один важный параметр – скорость R = k/n, которая характеризует степень избыточности кода, вводимой для обеспечения исправляющих свойств кода.

Как и блочные, сверточные коды могут быть систематическими и несистематическими и обозначаются как линейные сверточные (n,k)–коды.

Систематическим сверточным кодом является такой код, для которого в выходной последовательности кодовых символов содержится без изменения породившая его последовательность информационных символов. В противном случае сверточный код является несистематическим.

Примеры схем кодеров для систематического (8,4) и несистематического сверточных (6,3)–кодов приведены на рис. 12.7 и 12.8.

ля того, чтобы схема рис. 12.8 стала систематической, надо убрать один сумматор. Корректирующие свойства от того не изменятся, но у несистематического кода свёртка больше – это выгодно и нет информации в открытом виде.

Возможны различные способы описания сверточных кодов, например, с помощью порождающей матрицы. Правда, в силу бесконечности кодируемой последовательности и порождающая матрица будет иметь бесконечные размеры. Точнее, она будет состоять из бесконечного числа матриц M для обычного блочного кода, расположенных вдоль главной диагонали полубесконечной матрицы. Вся остальная ее часть заполняется нулями.

Однако более удобным способом описания сверточного кода является его задание с помощью импульсной переходной характеристики эквивалентного фильтра или соответствующего ей порождающего полинома.

Импульсная переходная характеристика фильтра (ИПХ)(а кодер сверточного кода, по сути дела, является фильтром) есть реакция на единичное воздействие вида 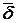= (10000. Для кодеров, изображенных на рис. 12.7 и 12.8, соответствующие импульсные характеристики будут иметь вид:

Еще одна форма задания сверточных кодов – это использование порождающих полиномов, однозначно связанных с ИПХ эквивалентного фильтра:

При этом кодовая последовательность F(x)на выходе сверточного кодера получается в результате свертки входной информационной последовательности G(x) с импульсной переходной характеристикой H.

Рассмотрим примеры кодирования последовательностей с использованием импульсной характеристики эквивалентного фильтра.

11.00.00.01.00.00…
11.00.00.01.00…

или G(x) = (1011000…

11.00.00.01.00.00.00…
11.00.00.01.00…
11.00.00.01…

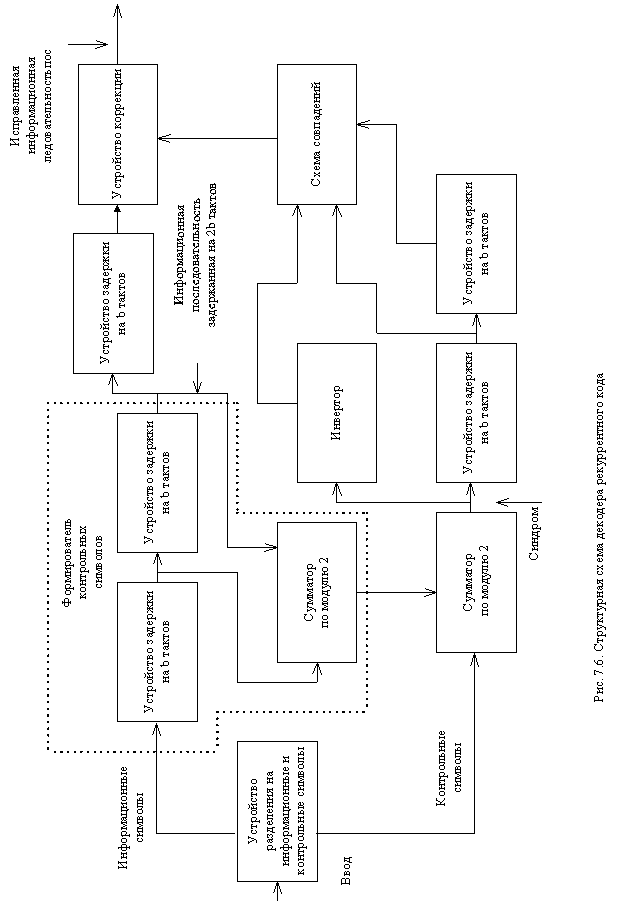
Иногда удобнее рассматривать полный порождающий полином сверточного кода P(x) как совокупность нескольких многочленов меньших степеней, соответствующих ячейкам выходного регистра кодера. Так, для кодера рис. 10.8 соответствующие частичные порождающие полиномы будут следующими:

Легко заметить, что при этом справедливы равенства

Такая форма записи удобна, поскольку видна структура кодирующего устройства (по набору полиномов можно сразу синтезировать устройство).

Дата добавления: 2016-02-04 ; просмотров: 5900 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник