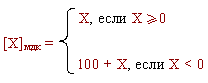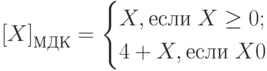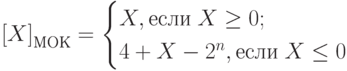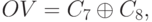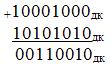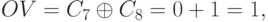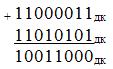сложение в модифицированном дополнительном коде
Модифицированные коды
Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.
При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.
Рассмотрим такой пример:
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим ещё один пример:
Можно заметить, что переполнение числовой сетки происходит в случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.
Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.
Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:
» + » ставится в соответствие 00
» – » ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного. Аналогично, по определению, обратным кодом является:
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
искажает младший знаковый разряд.
При этом различают два типа переполнения :
Лекция 7: Способы представления чисел в ЭВМ. Сложение чисел в обратном и дополнительном кодах
Модифицированные дополнительный и обратный коды и их использование в операции алгебраического суммирования
В модифицированных кодах кодирование знака осуществляется 2-мя разрядами:
При этом изображение числа X в этих кодах определяется равенствами:
Эта избыточность, сохраняя все качества обычных дополнительного и обратного кодов, дополняет их способностью фиксировать переполнение.
Знаковые разряды результата «01» определяют положительное переполнение в операциях алгебраического суммирования, а «10» – отрицательное.
При этом основная методика выполнения операций алгебраического суммирования в обратном и дополнительном кодах не меняется:
Данный метод, при всей его простоте и наглядности, практического применения в ЭВМ не нашел. В основном, это связано с его большой избыточностью при кодировании данных и потерями времени при выполнении операции и последующей интерпретации результата.
Метод на основе логического преобразования сигналов межразрядных переносов
В настоящее время практически во всех компьютерах роль модифицированных кодов выполняют переносы, идущие в знаковый и из знакового разряда. Определение факта наличия переполнения выполняется практически одновременно с выполнением самой операции суммирования по следующей формуле:
на примере восьмиразрядных операндов, где C7 – перенос в старший (знаковый) разряд, а C8 – перенос из знакового разряда.
Так при сложении операндов
произойдет переполнение разрядной сетки результата:
а при сложении операндов
нет, так как в данном случае: 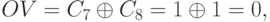
Такой подход требует использования всего лишь одного дополнительного элемента – «сумма по модулю два» – в сумматоре и практически не снижает его быстродействия.
Краткие итоги
В лекции рассмотрено представление чисел в прямом, обратном и дополнительном кодах. Особое внимание уделено дополнительному коду представления числа как наиболее распространенному в современных компьютерах. Показаны особенности алгебраического суммирования чисел в обратном и дополнительном кодах при различных сочетаниях операндов. Рассмотрены механизмы фиксации переполнения при выполнении операции алгебраического суммирования чисел.
Сложение двоичных чисел в модифицированных обратном и дополненном кодах
Привет, друзья!
Требуется решить задачу: Сложить X и Y, Y и Z в модифицированном обратном и модифицированном дополненном кодах. В случае появления признака переполнения увеличить число разрядов в кодах и повторить суммирование. Результат перевести в прямой код и проверить, пользуясь правилами двоичной арифметики.
Пожалуйста, распишите решение (в столбик) подробно и с объяснениями, т.к. я не нашёл достойной информации по модифицированным кодам.
Представление двоичных положительных и отрицательных чисел в обратном и дополнительном кодах
Нужно реализовать задание на языке с или с++, но я не знаю как это сделать. Задание: Представление.
Представление двоичных положительных и отрицательных чисел в обратном и дополнительном кодах
Как в программе Паскаль можно представлить двоичные положительные и отрицательные числа в обратном.
Сложение (вычитание) двоичных чисел в обратном коде
Сложение (вычитание) двоичных чисел в обратном коде.Можно не писать нахождение обратного кода
Помощь в написании контрольных, курсовых и дипломных работ здесь.
Сложение (вычитание) двоичных чисел в обратном коде
Помогите, пожалуйста. Сложение (вычитание) двоичных чисел в обратном коде с проверкой на.

Интересует алгоритм сложения и вычитания чисел в обратном коде(длина-8символов) Осуществлять.

Алгебраическое сложение целых положительных и отрицательных двоичных чисел в обратном коде.

Ускоренное Умножение в дополнительных модифицированных кодах со сдвигом сумматора, с анализом 2х.

нужно сложить 3 двоичных числа 11111+11000+11100 что-то я мучаюсь но ничего неполучается у меня.
Сложение и вычитание чисел со знаком в дополнительном коде



Содержание
4. Дополнительный код
5. Модифицированные обратные и дополнительные коды
6. Арифметические действия в машинных кодах.
Прямой код целого числа. Под прямым кодом двоичного числа понимают запись самого числа. Значение знакового разряда для положительных чисел определяют равным нулю (0), для отрицательных чисел — единице (1). Например, если для записи кода используется байт, то [1] :
| Число | Прямой код |
| +1101 | 0,0001101 |
| -1101 | 1,0001101 |
Крайний левый разряд в прямом коде нами отведен под знак числа, остальные разряды — под само число. Число располагаем в разрядной сетке так, чтобы цифра младшего разряда числа занимала крайнюю правую ячейку.
Знаковый разряд —> | 0, | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
Обратный код целого положительного числа совпадает с его прямым кодом. Для отрицательного числа обратный код строится заменой каждого незнакового байта его представления в прямом коде на противоположный (заменим 1 на 0, 0 на 1), знаковый разряд не изменяется.
| Число | Прямой код | Обратный код | Замечание |
| +11011 | 0,0011011 | 0,0011011 | Число положительное, обратный и прямой коды совпадают |
| -11011 | 1,0011011 | 1,1100100 | Число отрицательное, каждый байт, кроме знакового, изменен на противоположный |
Наиболее важные свойства обратного кода чисел:
· сложение положительного числа С с его отрицательным значением в обратном коде дает т.н. машинную единицу МЕок=1|11…11, состоящую из единиц в знаковом и в значащих разрядах числа;
· нуль в обратном коде имеет двоякое значение. Он может быть как положительным числом – 0|00…00, так и отрицательным 1|11…11. Значение отрицательного числа совпадает с МЕок. Двойственное представление 0 явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
| Число | Прямой код | Обратный код | Дополнительный код |
| + 1110 | 0,0001110 | 0,0001110 | 0.0001110 |
| -1110 | 1,0001110 | 1,1110001 | 1,1110010 |
Основные свойства дополнительного кода:
· сложение дополнительных кодов положительного числа С с его отрицательным значением дает т.н. машинную единицу дополнительного кода:
МЕдк=МЕок + 2 0 = 10|00…00, т.е. число 10 (два) в знаковых разрядах числа;
· дополнительный код называется так потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.
Модифицированные обратные и дополнительные коды
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. В модифицированных обратном и дополнительном кодах под знак числа отводится не один, а два разряда: «00» соответствует знаку «плюс», «11» — знаку «минус». Любая другая комбинация («01» или «10»), получившаяся в знаковых разрядах, является признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем, не отличается от сложения в обычных обратном и дополнительном кодах.
Сложение и вычитание чисел со знаком в дополнительном коде
Если оба числа имеют n–разрядное представление, то алгебраическая сумма будет получена по правилам двоичного сложения (включая знаковый разряд), если отбросить возможный перенос из старшего разряда. Если числа принадлежат диапазону представимых данных и имеют разные знаки, то сумма всегда будет лежать в этом диапазоне. Переполнение может иметь место, если оба cлагаемых имеют одинаковые знаки.
Пример 1:
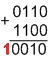

Арифметические действия в машинных кодах.
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.
| Требуемая операция | Необходимое преобразование |
| А+В | А+В |
| А-В | А+(-В) |
| -А+В | (-А)+В |
| -А-В | (-А)+(-В) |
Здесь А и В неотрицательные числа. Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей. При выполнении сложения цифр необходимо соблюдать следующие правила:
1. Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
2. Знаковые разряды участвуют в сложении так же, как и значащие.
3. Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
4. При преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 1. Сложить два числа: А10 = 7, В10 = 16.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
Сложение в обратном или дополнительном коде дает один и тот же результат:
По таблице необходимо преобразование А+(-В), в которой второй член преобразуется с учетом знака
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (п.4 правил). В случае ДК этот перенос игнорируется.
3.6.Сложение в обратных кодах чисел разных знаков
Рассматриваемые ниже случаи сложения чисел разного знака имеют следующие особенности
1. при сложении чисел разных знаков переполнение невозможно. Модуль суммы в этом случае всегда меньше модуля максимального и представимого в заданной разрядной сетке слагаемого;
2. знак суммы зависит, в отличие от ранее рассмотренных случаев, не только от знаков слагаемых, но и от соотношения их модулей.
3. в зависимости от соотношения модулей, сумма может формироваться или в прямом или в обратном кодах.
3.1.6.1. Модуль положительного операнда больше модуля отрицательного. (Случаи 6, 9)
Пусть, А,В – операнды, отвечающие соотношениям
для случая 6: А ³0 и В£0. Кроме того, | А |³| В |.
для случая 9: A£ 0 и B³0 Кроме того, | А |£ | В |
Выполняемое сложение при этих условиях эквивалентно соответственно вычитаниям (А– В) и (В–А). Разность, априори, положительна. Отрицательный операнд складывается в обратном коде.
В обоих случаях должен возникать подсуммируемый в младший разряд суммы перенос.
Как для дробных, так и для целых чисел в результате сложения в обеих рассматриваемых случаях должен формироваться прямой код положительной разности.

Выполнить сложение в обратном коде пар дробных и целых отрицательных операндов соответственно А,В и X,Y.
Дробные слагаемые равны
Целые слагаемые равны
Предварительные выводы. Предварительное сложение приводит к результатам A+B=0, 510 –0,062510=0,4375 10=0,01110002; X+Y= –1910+5110= 3210.= 0 01000002.
Должны быть получены положительные суммы, представленные в прямом коде.
Кроме того, следует ожидать переносы из знаковых разрядов дробных и целых сумм.
Решение. Отрицательные операнды преобразуются в обратный код.
Обратный код дробного слагаемого В равен
Обратный код целого слагаемого X равен
Сложение в двоичных обратных кодах имеет вид:
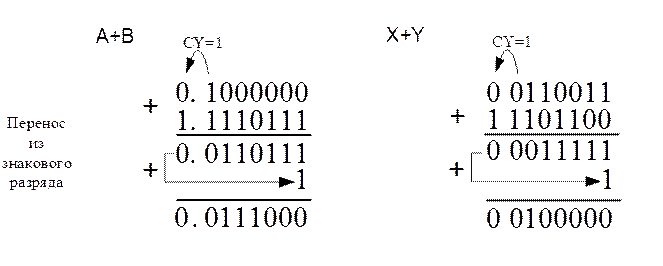 |

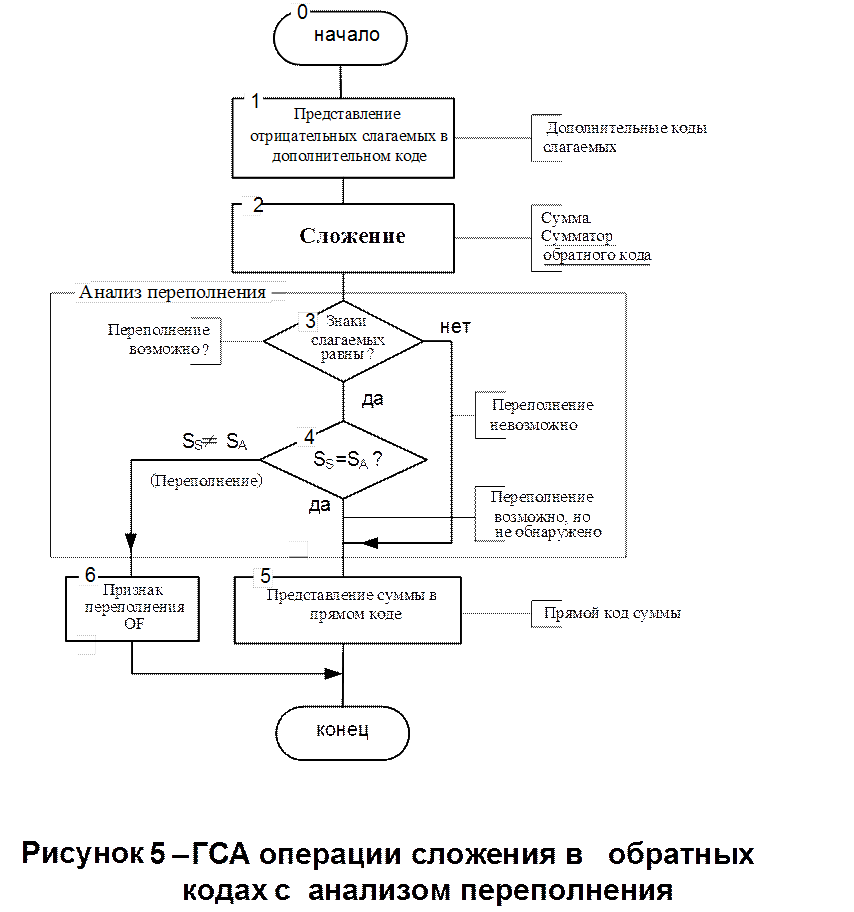
3.4 Обнаружение переполнения разрядной сетки в ПОК
На рисунке 3 представлен алгоритм обнаружения переполнения путем сравнения знаков. Алгоритм аналогичен по логической структуре с рассмотренным ранее алгоритмом обнаружения переполнения для дополнительных кодов. Отличие состоит в отсутствии проверки на особый случай переполнения разрядной сетки, что является преимуществом обратных кодов.
 |
4. Cложение чисел в модифицированных дополнительных кодах (МДК)
Модифицированные коды упрощают процедуру обнаружения переполнения.
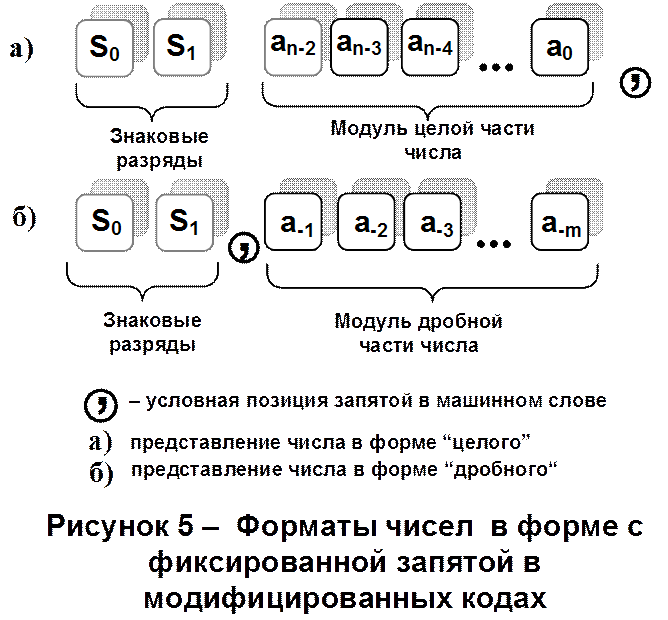 |
В модифицированных кодах для кодирования знака используются не один, как в простых кодах а два разряда S0, S1. т.е. для представления слагаемого вводится дополнительный разряд. (Рис.5)
Комбинация значений “00” используется как код знака “+”, а комбинация “11” как код знака “–”. В модифицированном коде может быть представлен как прямой, так и обратный и дополнительный коды (Рис.6).
Процедура 3. Основные правила сложения в модифицированных дополнительных кодах:
1. положительные операнды участвуют в сложении в прямых модифицированных кодах;
Чтобы распечатать файл, скачайте его (в формате Word).