сортировка подсчетом c код
Сортировка подсчётом
Сортировка подсчётом (англ. counting sort) — алгоритм сортировки целых чисел в диапазоне от [math]0[/math] до некоторой константы [math]k[/math] или сложных объектов, работающий за линейное время.
Содержание
Сортировка целых чисел [ править ]
Это простейший вариант алгоритма.
Описание [ править ]
Псевдокод [ править ]
Сортировка сложных объектов [ править ]
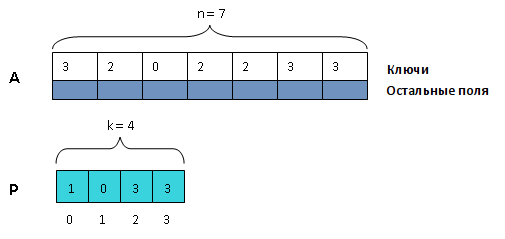
Сортировка целых чисел за линейное время это хорошо, но недостаточно. Иногда бывает очень желательно применить быстрый алгоритм сортировки подсчетом для упорядочивания набора каких-либо «сложных» данных. Под «сложными объектами» здесь подразумеваются структуры, содержащие в себе несколько полей. Одно из них мы выделим и назовем ключом, сортировка будет идти именно по нему (предполагается, что значения, принимаемые ключом — целые числа в диапазоне от [math]0[/math] до [math]\mathrm k-1[/math] ).
Мы не сможем использовать здесь в точности тот же алгоритм, что и для сортировки подсчетом обычных целых чисел, потому что в наборе могут быть различные структуры, имеющие одинаковые ключи. Существует два способа справиться с этой проблемой — использовать списки для хранения структур в отсортированном массиве или заранее посчитать количество структур с одинаковыми ключами для каждого значения ключа.
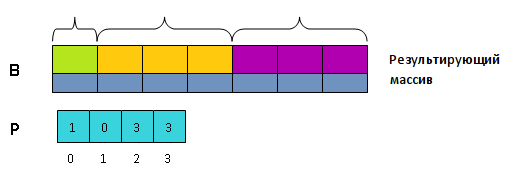
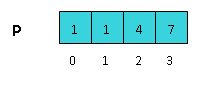
Описание [ править ]
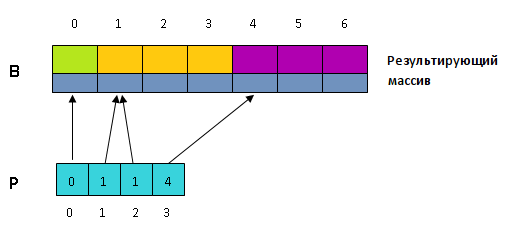
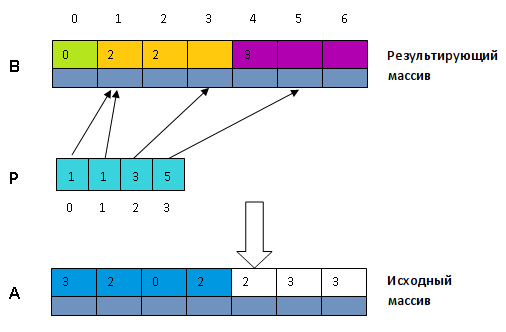
Таким образом после завершения алгоритма в [math]B[/math] будет содержаться исходная последовательность в отсортированном виде (так как блоки расположены по возрастанию соответствующих ключей).
Псевдокод [ править ]
Здесь шаги 3 и 4 из описания объединены в один цикл. Обратите внимание, что в последнем цикле инструкцией
копируется структура [math]A[i][/math] целиком, а не только её ключ.
Анализ [ править ]
Алгоритм работает за линейное время, но является псевдополиномиальным.
Поиск диапазона ключей [ править ]
Counting Sort Algorithm
In this tutorial, you will learn about the counting sort algorithm and its implementation in Python, Java, C, and C++.
Counting sort is a sorting algorithm that sorts the elements of an array by counting the number of occurrences of each unique element in the array. The count is stored in an auxiliary array and the sorting is done by mapping the count as an index of the auxiliary array.
Working of Counting Sort
Counting Sort Algorithm
Counting Sort Code in Python, Java, and C/C++
Complexity
| Time Complexity | |
|---|---|
| Best | O(n+k) |
| Worst | O(n+k) |
| Average | O(n+k) |
| Space Complexity | O(max) |
| Stability | Yes |
Time Complexities
There are mainly four main loops. (Finding the greatest value can be done outside the function.)
| for-loop | time of counting |
|---|---|
| 1st | O(max) |
| 2nd | O(size) |
| 3rd | O(max) |
| 4th | O(size) |
Overall complexity = O(max)+O(size)+O(max)+O(size) = O(max+size)
In all the above cases, the complexity is the same because no matter how the elements are placed in the array, the algorithm goes through n+k times.
There is no comparison between any elements, so it is better than comparison based sorting techniques. But, it is bad if the integers are very large because the array of that size should be made.
Space Complexity
Counting Sort Applications
Counting sort is used when:
Подсчет Сортировка
Подсчет сортировки — это метод сортировки, основанный на ключах между определенным диапазоном. Он работает путем подсчета количества объектов, имеющих различные ключевые значения (вид хеширования). Затем делаем некоторую арифметику, чтобы вычислить положение каждого объекта в выходной последовательности.
Позвольте нам понять это с помощью примера.
Ниже приведена реализация сортировки отсчетов.
// C ++ Программа для подсчета сортировки
#include
#include
using namespace std;
// Основная функция такого рода
// заданная строка arr [] в
// алфавитный порядок
void countSort( char arr[])
// Выходной массив символов
// это будет отсортировано обр
char output[ strlen (arr)];
// Создание массива count для хранения счетчика inidividul
// символы и инициализируем массив count как 0
int count[RANGE + 1], i;
memset (count, 0, sizeof (count));
// Сохраняем количество каждого символа
// Изменить count [i] так, чтобы count [i] теперь содержал фактический
// положение этого символа в выходном массиве
// Создаем массив выходных символов
Для стабильного алгоритма
Для логики: см. Реализацию
// Копируем выходной массив в arr, так что теперь arr
// содержит отсортированные символы
char arr[] = «geeksforgeeks» ;
cout «Sorted character array is «
// Этот код предоставлен rathbhupendra
// C Программа для подсчета сортировки
#include
#include
#define RANGE 255
// Основная функция, которая сортирует заданную строку arr [] в
// алфавитный порядок
void countSort( char arr[])
// Выходной массив символов, который будет отсортирован
char output[ strlen (arr)];
// Создание массива count для хранения счетчика inidividul
// символы и инициализируем массив count как 0
int count[RANGE + 1], i;
memset (count, 0, sizeof (count));
// Сохраняем количество каждого символа
// Изменить count [i] так, чтобы count [i] теперь содержал фактический
// положение этого символа в выходном массиве
// Создаем массив выходных символов
Для стабильного алгоритма
Для логики: см. Реализацию
// Копируем выходной массив в arr, так что теперь arr
// содержит отсортированные символы
// Программа драйвера для проверки вышеуказанной функции
char arr[] = «geeksforgeeks» ; // «applepp»;
// Java-реализация Counting Sort
void sort( char arr[])
// Выходной массив символов, который будет отсортирован
char output[] = new char [n];
// Создание массива count для хранения счетчика inidividul
// символы и инициализируем массив count как 0
int count[] = new int [ 256 ];
for ( int i= 0 ; i 256 ; ++i)
// сохранить количество каждого символа
// Изменить count [i] так, чтобы count [i] теперь содержал фактический
// положение этого символа в выходном массиве
for ( int i= 1 ; i 255 ; ++i)
// Создаем массив выходных символов
// Чтобы сделать его стабильным, мы работаем в обратном порядке.
for ( int i = n- 1 ; i>= 0 ; i—)
output[count[arr[i]]- 1 ] = arr[i];
// Копируем выходной массив в arr, так что теперь arr
// содержит отсортированные символы
public static void main(String args[])
CountingSort ob = new CountingSort();
System.out.print( «Sorted character array is » );
>
/ * Этот код предоставлен Раджатом Мишрой * /
# Python программа для подсчета сортировки
# Основная функция, которая сортирует заданную строку arr [] в
# Алфавитный порядок
# Выходной массив символов, который будет иметь отсортированный обр
output = [ 0 for i in range ( 256 )]
# Создайте массив count для хранения счетчика inidividul
# символов и инициализировать массив count как 0
count = [ 0 for i in range ( 256 )]
# Для хранения полученного ответа, так как
ans = [«» for _ in arr]
# Хранить количество каждого персонажа
# Измените count [i] так, чтобы count [i] теперь содержал фактический
# позиция этого символа в выходном массиве
for i in range ( 256 ):
# Построить выходной массив символов
for i in range ( len (arr)):
# Скопируйте выходной массив в arr, так что теперь arr
# содержит отсортированные символы
for i in range ( len (arr)):
# Программа драйвера для проверки вышеуказанной функции
print «Sorted character array is %s» % («».join(ans))
# Этот код предоставлен Nikhil Kumar Singh
// C # реализация Counting Sort
static void countsort( char []arr)
// Выходной массив символов, который
// будет отсортирован обр
char []output = new char [n];
// Создаем массив count для хранения
// количество символов inidividul
// и инициализируем массив count как 0
int []count = new int [256];
// сохранить количество каждого символа
// Изменим count [i] так, чтобы count [i]
// теперь содержит актуальную позицию
// этот символ в выходном массиве
// Создаем массив выходных символов
// Чтобы сделать его стабильным, мы работаем в обратном порядке.
for ( int i = n-1; i>=0; i—)
// Копируем выходной массив в arr, так
// этот arr теперь содержит отсортированный
public static void Main()
Console.Write( «Sorted character array is » );
// Этот код предоставлен Sam007.
// PHP программа для подсчета сортировки
// Основная функция такого рода
// заданная строка arr [] в
// алфавитный порядок
// Выходной массив символов
// это будет отсортировано обр
// Создаем массив count для
// сохраняем количество inidividul
// символы и инициализация
// считать массив как 0
// Изменим count [i] так, чтобы
// count [i] теперь содержит
// фактическая позиция этого
// символ в выходном массиве
// Чтобы сделать его стабильным, мы работаем
// в обратном порядке.
// Копируем выходной массив в
// содержит отсортированные символы
$arr = «geeksforgeeks» ; // «applepp»;
// Этот код предоставлен mits
?>
Выход:
Сложность времени: O (n + k), где n — количество элементов во входном массиве, а k — диапазон входных данных.
Вспомогательное пространство: O (n + k)
Проблема с предыдущей сортировкой была в том, что мы не могли отсортировать элементы, если в них есть отрицательные числа. Потому что нет отрицательных индексов массива. Итак, что мы делаем, мы находим минимальный элемент и будем хранить количество этого минимального элемента при нулевом индексе.
// Считаем сортировку, которая также принимает отрицательные числа
#include
#include
#include
using namespace std;
void countSort(vector int >& arr)
int max = *max_element(arr.begin(), arr.end());
int min = *min_element(arr.begin(), arr.end());
vector int > count(range), output(arr.size());
for ( int i = arr.size()-1; i >= 0; i—)
void printArray(vector int > & arr)
// Считаем сортировку, которая также принимает отрицательные числа
static void countSort( int [] arr)
int max = Arrays.stream(arr).max().getAsInt();
int min = Arrays.stream(arr).min().getAsInt();
int count[] = new int [range];
int output[] = new int [arr.length];
static void printArray( int [] arr)
public static void main(String[] args)
// Этот код предоставлен princiRaj1992
Очки, которые следует отметить:
1. Подсчет сортировки эффективен, если диапазон входных данных не намного превышает количество сортируемых объектов. Рассмотрим ситуацию, когда входная последовательность находится в диапазоне от 1 до 10K, а данные — 10, 5, 10K, 5K.
2. Это не сортировка на основе сравнения. Его сложность во время выполнения составляет O (n) с пространством, пропорциональным диапазону данных.
3. Он часто используется как подпрограмма для другого алгоритма сортировки, такого как сортировка по основанию.
4. Подсчет сортировки использует частичное хеширование для подсчета вхождения объекта данных в O (1).
5. Счетная сортировка может быть расширена для работы и для отрицательных входных данных.
Упражнение:
1. Измените приведенный выше код, чтобы отсортировать входные данные в диапазоне от M до N.
2. Является ли счет сортировки стабильным и онлайн?
3. Мысли о распараллеливании алгоритма сортировки отсчетов.
Фотосъёмка:
Тест на подсчет сортировки
Практика кодирования для сортировки
Нужно объяснение сортировки подсчетом
Может кто-то доступно объяснить алгоритм сортировки подсчётом(не в конкретном языке программирования,а в абстрагированном варианте). Читаю книгу Томаса Кормена «Алгоритмы вводный курс». Дошёл до сортировки подсчётом. ну уже наверно раз 20 перечитал в том числе и пример. не доходит. я не знаю. может перевод такой или я)
3 ответа 3
Попробуем наглядно представить происходящее. Предположим, у нас есть числа:
Генерируем из них массив A[i] = N, в котором эти числа являются индексом, а значением N является количество вхождений каждого числа в начальный набор:
Теперь просто идём по этому массиву (в естественном порядке его индексов) и выводим индекс массива N раз:
Идея алгоритма заключается в подсчёте кол-ва каждого элемента и использования этой информации (а также диапазона значений элементов) для сортировки последовательности.
диапазоном каждого числа от [0, 5]
1) Создаётся допольнительный массив С размером K = 6 (верхняя граница диапазона значений (5) + 1) для хранения количеств каждого элемента
2) Перезаписываем элементы массива A следующим образом
Собственно, ключевой особенностью это алгоритма является то, что имея сравнительно малый с кол-вом элементов последовательности диапазон значений можно получить почти линейную от диапазона значений O(K) скорость работы засчёт малых итераций внешнего цикла.
Сортировки — квадратичные и сортировка слиянием
Мы считаем, что вы уже знаете и умеете следующие вещи: * основы языков Python, C++ или Java (примеры в конспектах будут только на C++) * оператор if * циклы for и while * создание функций * концепцию рекурсии * поиск минимума в массиве
Квадратичные сортировки
Задание
Какие вы знаете алгоритмы сортировки?
Если вы не знаете ни одного алгоритма, то придумайте какой-нибудь разумный алгоритм сами.
Сортировка пузырьком
Это самый популярный алгоритм сортировки, хоть он и не самый очевидный.
Ссылка на красивую визуализацию: https://visualgo.net/nl/sorting
Заметьте, как каждую итерацию максимальный элемент “всплывает как пузырек” к концу массива.
Заметьте, что после \(i\) шагов алгоритма сортировки пузырьком последние \(i + 1\) чисел всегда отсортированы. Именно поэтому алгоритм и работает.
И именно поэтому его можно немного ускорить.
Задание
Подумайте, какие лишние элементы мы перебираем. Как нужно изменить границы в двух циклах for, чтобы не делать никаких бесполезных действий?
Сортировка выбором
Более понятным и придумываемым способом является сортировка выбором минимума (или максимума).
Сортировка вставками
Также существует сортировка вставками.
Префиксом длины \(i\) будем называть первые \(i\) элементов массива.
Задание
Сдайте 4 первые задачи в контесте:
При сдаче задач нельзя пользоваться встроенной сортировкой!
Сортировка подсчетом
Предыдущие три алгоритма работали с массивами, в которых лежат абсолютно любые объекты, которые можно сравнивать. Любые числа, строки, пары, другие массивы, почти все что угодно.
Но в особых случаях, когда элементы принадлежат какому-то маленькому множеству, можно использовать другой алгоритм — сортировку подсчетом.
Пусть, например, нам гарантируется, что все числа натуральные и лежат в промежутке от 1 до 100.
Задание
Сдайте 5, 6 и 7 задачи в контесте:
При сдаче задач нельзя пользоваться встроенной сортировкой!
О-нотация
Очень часто требуется оценить, сколько времени работают эти алгоритмы. Но тут возникают проблемы:
Зачастую основной задачей программиста становится оптимизировать алгоритм, выполнение которого займёт тысячи лет, до какого-нибудь адекватного времени работы. Поэтому хотелось бы уметь предсказывать, сколько времени займёт выполнение алгоритма ещё до того, как мы его запустим.
Для этого давайте для начала попробуем оценить число операций в алгоритме.
Задание
И также посчитайте точное число присваиваний в сортировках пузырьком, выбором, вставками и подсчетом в худшем случае. Давайте считать, что swap — это 3 присваивания.
В худшем случае алгоритмы работают за столько сравнений:
Также не сразу очевидно, какой из этих алгоритмов работает быстрее. Сравнивать формулы сложно. Хочется придумать способ упростить эти формулы так, чтобы:
В таких обозначениях можно сказать, что * Сортировка пузырьком работает за \(O(N^2)\) * Сортировка выбором работает за \(O(N^2)\) * Сортировка вставками работает за \(O(N^2)\) * Сортировка подсчетом работает за \(O(N + M)\)
Задание
Задание
Найдите асимптотическое время работы данных функций:
Задание
Найдите лучшее время работы алгоритмов, решающих данные задачи: * Написать числа от \(1\) до \(N\) * Написать все тройки чисел от \(1\) до \(N\) * Найти разницу между максимумом и минимумом в массиве * Найти число единиц в бинарной записи числа \(N\)
Сортировка слиянием* (для тех, кто всё успевает)
Возникает вопрос: а бывают ли сортировки, которые быстрее, чем квадратиные, и работают всегда?
Давайте подробнее рассмотрим сортировку слиянием, она же MergeSort.
Ссылка на красивую визуализацию: https://visualgo.net/nl/sorting (вкладка MER)
Для удобства написания кода фунции можно сделать вот такими:
Задание
Разобраться, реализовать сортировку слиянием и сдать последнюю задачу в этом контесте:
Применение сортировки для решения задач
Задание
Решить как можно больше задач из этого контеста:
В этом контесте можно и нужно использовать встроенную сортировку sort.