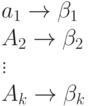средняя длина равномерного кода
Равномерные и неравномерные коды.
Дата добавления: 2015-08-14 ; просмотров: 33163 ; Нарушение авторских прав
Код называется равномерным (или кодом постоянной длины), если все его кодовые слова содержат одинаковое число букв (одинаковую длину слов). Соответственно, кодирование называется равномерным, если соответствующий ему код имеет постоянную длину. В настоящее время в информатике более употребительно равномерное кодирование, оно проще и более удобно. В компьютерах при кодировании информации в основном используются равномерные коды, соответствующие размерам компьютерных ячеек.
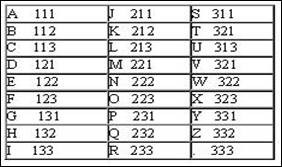
Другим интересным примером равномерного кода является код Трисиме, в котором знакам латинского алфавита ставятся в соответствие кодовые слова длины 3 над алфавитом из 3-х символов: <1, 2, 3>. Этот код представлен в следующей таблице :
Понятно, что код Трисиме не может кодировать более чем 3 3 =27 символов.
Число букв в алфавите кода называется основанием кода, а длина кодовых слов равномерного кода называется порядком кода. Коды с основанием 2, как уже говорилось, называются двоичными, а с основанием 3 – троичными, и так далее. Так код Бодо имеет основание 2, а порядок 5, а у кода Трисиме и основание, и порядок равны 3.
Код называется неравномерным (или кодом переменной длины), если его кодовые слова имеют разное число букв (неодинаковую длину слов). Соответственно, кодирование называется неравномерным, если соответствующий ему код неравномерный.
Типичным примером неравномерного кода является телеграфный код, который принято называть азбукой Морзе. На следующей таблице представлен код азбуки Морзе для русского алфавита:
| A | • − | И | • • | P | • − • | Ш | − − − − | • − − − − | − − − − • | |
| Б | − • • • | Й | • − − − | С | • • • | Щ | − − • − | • • − − − | − − − − − | |
| В | • − − | К | − • − | Т | − | Ъ | • − − • − • | • • • − − | Точка | • • • • • • |
| Г | − − • | Л | • − • • | У | • • − | Ь | − • • − | • • • • − | Запятая | • − • − • − |
| Д | − • • | М | − − | Ф | • • − • | Ы | − • − − | • • • • • | / | − • • − • |
| Е | • | H | − • | Х | • • • • | Э | • • − • • | − • • • • | ? | • • − − • • |
| Ж | • • • − | О | − − − | Ц | − • − • | Ю | • • − − | − − • • • | ! | − − • • − − |
| З | − − • • | П | • − − • | Ч | − − − • | Я | • − • − | − − − • • | @ | • − − • − • |
Американский изобретатель телеграфа Сэмюель Морзе разработал этот код в 1838 году для передачи телеграфных сообщений в виде последовательности электрических сигналов, передаваемых от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Этот код был придуман Морзе задолго до научных исследований
 |
| СэмюэлМорзе (1791-1872) |
относительной частоты появления различных букв в текстах, но, тем не менее, Морзе при составлении кода использовал принцип частоты букв. Буквам, используемым чаще, им присвоены короткие кодовые комбинации, редко используемым буквам – длинные. Морзе оценил относительную частоту букв английского языка подсчетом литер в ячейках типографской наборной машины. Наиболее часто используемой букве «Е» (в английском языке) он присвоил наиболее короткий код «точка». Следующей по количеству литер букве он присвоил код несколько большей длительности и так далее.
При составлении азбуки Морзе для букв русского алфавита учет относительной частоты букв не производился, и это повысило его избыточность. Расчеты избыточности кода Морзе на основании проведенных исследований частоты появления букв показали, что для букв английского алфавита она составляет 19%, для букв русского алфавита 22%.
Преимущество у неравномерных кодов перед равномерными как раз и состоит в том, что сообщения можно передавать более экономным способом, так как часто передаваемые кодовые слова более короткие, а значит, кодовая последовательность может иметь меньшую длину, чем для равномерных кодов. Ниже это будет показано.
Но у неравномерных кодов есть серьезный недостаток по сравнению с равномерными кодами. У равномерных кодов кодовая последовательность всегда декодируется однозначно за счет того, что кодовые слова имеют одинаковую длину (кодовая последовательность легко делится на кодовые слова). Но не для всех неравномерных кодов достигается однозначность декодирования кодовых последовательностей. Мы уже видели это, пытаясь рассматривать азбуку Морзе как двоичный код.
Этот код неравномерный (кодовые слова разной длины).
Закодируем последовательность сообщений: s7s7. Имеем F(s7s7)=B=111111. Но эта последовательность может быть декодирована и по-другому, так как: B=F(s3s3s3)= F(s1s3s7)=F(s3s7s1)=F(s1s1s1s1s1s1s1s). Как видим, способов декодирования много (подсчитайте: сколько их?). Неоднозначно декодируется и следующая последовательность:
11011011 (а сколько здесь способов декодирования?). Очевидно, что такой код практически использовать нельзя. А если мы изменим код так, чтобы он стал равномерным, например, доопределим функцию F так:
то теперь никаких проблем с декодированием не будет.
Информационные технологии
Неравномерное кодирование. Средняя длина кодирования
В приведенных выше примерах кодирования все кодовые слова имели одинаковую длину. Однако это не является обязательным требованием. Более того, если вероятности появления сообщений заметно отличаются друг от друга, то сообщения с большой вероятностью появления лучше кодировать короткими словами, а более длинными словами кодировать редкие сообщений. В результате кодовый текст при определенных условиях станет в среднем короче.
Наиболее экономным является код с наименьшей средней длиной 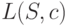
Пусть источник содержит 4 сообщения 


 | 00 |
 | 01 |
| A_3 | 10 |
| A_4 | 11 |
Очевидно, что для представления (передачи) любой последовательности в среднем потребуется 2 знака на одно сообщение. Сравним эффективность такого кодирования с описанным выше кодированием словами переменной длины. Кодовая таблица для данного случая может иметь следующий вид.
 | 0 |
 | 1 |
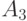 | 10 |
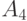 | 11 |
В этой таблице, в отличие от предыдущей, наиболее частые сообщения 

в то время как для равномерного кода средняя длина 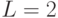
Необходимо отметить, что неоднозначность декодирования слова появилась несмотря на то, что условие однозначности декодирования знаков (инъективность кодового отображения) выполняется.
Решение данной проблемы заключается в том, чтобы иметь возможность в любом кодовом тексте выделять отдельные кодовые слова без использования специальных разделительных знаков. Иначе говоря, необходимо, чтобы код удовлетворял следующему требованию: всякая последовательность кодовых знаков может быть единственным образом разбита на кодовые слова. Коды, для которых последнее требование выполнено, называются однозначно декодируемыми (иногда их называют кодами без запятой).
Рассмотрим код (схему алфавитного кодирования) 
и различные слова, составленные из элементарных кодов.
Определение. Код 
Если таблица кодов содержит одинаковые кодовые слова, то есть если
то код заведомо не является однозначно декодируемым (схема не является разделимой). Такие коды далее не рассматриваются.
Префиксные коды
Наиболее простыми и часто используемыми кодами без специального разделителя кодовых слов являются так называемые префиксные коды [29].
Теорема 1. Префиксный код является однозначно декодируемым.
Множество кодовых слов можно графически изобразить как поддерево словарного дерева (рис.6.5). Для этого из всего словарного дерева следует показать только вершины, соответствующие кодовым словам, и пути, ведущие от этих вершин к корню дерева. Такое поддерево называют деревом кода или кодовым деревом.
Замечание. Свойство префиксности является достаточным, но не является необходимым для однозначной декодируемости.
Если код префиксный, то, читая кодовую запись подряд от начала, мы всегда сможем разобраться, где кончается одно кодовое слово и начинается следующее. Если, например, в кодовой записи встретилось кодовое обозначение 110, то разночтений быть не может, так как в силу префиксности наш код не содержит кодовых обозначений 1, 11 или, скажем, 1101. Именно так обстояло дело для рассмотренного выше кода, который очевидно является префиксным.
Средняя длина равномерного кода
Здравствуйте! Меня зовут Александр Георгиевич. Я являюсь профессиональным репетитором в области информационных технологий, математике, баз данных и программирования.
Если у вас возникли затруднения с обработкой равномерного или неравномерного кода, то срочно записывайтесь ко мне на первый пробный урок, на которых мы с вами очень детально разберем все ваши вопросы и прорешаем большое количество различных тематических упражнений.
Чтобы гарантированно набрать на официальном экзамене ОГЭ или ЕГЭ по информатике высоченный балл берите сотовый телефон, дозванивайтесь до меня и задавайте любые интересующие вопросы.
Рекомендую использовать формат дистанционного обучения! Это выгодно, удобно и эффективно!
Что такое равномерный код и в каких случаях его применяют?
Допустим, вам требуется написать секретное письмо и отправить его своему другу. Вы – человек, проживающий на территории России, следовательно, использующий для написания слов буквы русского алфавита. И, вот, вы решаете закодировать ваше послание двоичным кодом, то есть вместо русских слов ваш друг получит набор цепочек, состоящий из нулей и единиц.
Но ваш соратник без особых проблем сможет провести дешифрацию вашего информационного сообщения, так как вы ему расскажете об алгоритме шифрации/дешифрации.
Символ
Равномерный код
Десятичное представление
Равномерный код – такой код, когда все символы какого-либо алфавита кодируются кодами одинаковой длины.
Что такое неравномерный код и в каких случаях его применяют?
Чтобы глубоко понять смысл неравномерного кодирования давайте представим, что вы работаете на продуктовом складе. Вы хотите оптимизировать свою работу и закодировать название каждого товара минимально возможным количеством бит.
На ум приходит вариант с равномерным кодом, то есть закодировать название каждого продукта информационным кодом одинаковой длины. Но в данном случае это не самый оптимальный вариант кодирования. Почему? Потому что один товар является наиболее популярным и востребованным, и вам, как кладовщику, приходится чаще с ним взаимодействовать.
Следует понять общий принцип неравномерного кода: суть его в том, чтобы кодировать наиболее часто используемые элементы как можно меньшим количеством бит, так как ими вы оперируете очень часто.
Неравномерный код – такой код, когда все элементы какого-либо множества кодируются кодом различной длины.
Данные четыре товара покупают огромными партиями и вы уже устали вести записи в базе данных постоянно вбивая названиях этих продуктов. Давайте применим следующее кодирование:
Итого, нам потребовалось два бита информации, чтобы закодировать в бинарном виде наиболее ходовых четыре товара.
А как поступить с наименее популярными товарами, например, муку и перец также достаточно часто покупают. В этом случае данные товары можно запрограммировать так:
Вы должны уловить общий принцип: чем наименее популярный товар, тем большим количеством бит он будет закодирован.
И все бы хорошо, но есть одна существенная проблема, возникающая при создании неравномерного кода, – проблема с однозначной дешифрацией. Для полного понимания данной проблемы вам следует познакомиться с условием Фано.
Равномерный код vs неравномерный код
Чтобы хорошо понимать в каких ситуациях стоит применять то или иное кодирование, вам нужно очень хорошо разобраться с частотой использования элементов, которые вы планируете закодировать. Если частота применения приблизительно равна у всех элементов, то смело применяйте равномерный код, в других случаях – неравномерный код.
А сейчас я вам предлагаю ознакомиться с мультимедийным решением, в котором я показываю, как правильно оперировать равномерным и неравномерным кодом.
Я хочу записаться к вам на индивидуальный урок по информатике и ИКТ
Если у вас остались какие-либо вопросы по рассматриваемой теме, то записывайтесь ко мне на первый пробный урок. Я репетитор-практик, следовательно, на своих уроках я уделяю максимум внимания решению заданий. Из теории лишь записываются самые базовые сведения: определения, тезисы, формулировки теорем и аксиом.
Специально для своих потенциальных клиентов я разработал стабильную многопараметрическую систему, состоящую из 144 вариантов нашего будущего взаимовыгодного сотрудничества. Даже самый взыскательный клиент сумеет выбрать вариант, полностью покрывающий его запросы.
Не откладывайте свое решение в долгий ящик. Я все-таки достаточно востребованный и квалифицированный репетитор, поэтому звоните прямо сейчас – количество ученических мест ограниченно!
Средняя длина равномерного кода
Кодирование чисел с помощью нулей и единиц впервые применил в своей (механической)
вычислительной машине немецкий мыслитель Готфрид Вильгельм Лейбниц в конце XVII века. Затем, уже в середине XX века, двоичное кодирование информации стало повсеместно
применяться для электронных компьютеров.
Чаще всего используется равномерный код, когда все символы исходного сообщения
кодируются с помощью одинакового количества двоичных знаков. Например,
Здесь использовано 4 символа (А…Г), поэтому понадобилось 2 бита (2 разряда в двоичном числе) для кодирования.
Если бы использовали 8 символов, то нужно было бы 3 бита.
Сколько бит понадобится для кодирования 32 символов?
Как ты думаешь, чем отличается равномерный код от неравномерного?
Например, для кодирования первых 5 букв русского алфавита используется таблица
Это неравномерный код, поскольку в нем есть двух ‐ и трехсимвольные коды.
Как декодировать сообщение 1100000100110, зная ключ?
Букв с кодами 1 и 11 в таблице нет, поэтому сообщение начинается с буквы Г – она имеет код 110:
Следующий (единственно возможный) код – 000, это буква А:
Аналогично декодируем все сообщение:
В общем случае декодировать сообщение удается только перебором вариантов. Например,
декодируем сообщение 010100111101, закодированное с помощью кодовой таблицы
Декодировать сразу, скорее всего, не удастся. На первом месте может быть, буква А или буква Б. Сначала предположим, что это буква А:
Тогда второй буквой также может быть буква А:
Дальше декодировать не получается, потому что в таблице нет кодов 0, 00 и 001. Поэтому
проверяем второй вариант: вторая буква – Б:
Третьей буквой может быть А:
Тогда четвертая и пятая буквы определяются однозначно – это буквы Г и Д. Таким образом, один
1.Для кодирования сообщения используется таблица
1.2. Преобразование сообщения в сигналы
1.2.1. Кодирование сообщений
Процесс передачи информации заключается в том, что сообщения преобразуются в сигналы и по системе связи передаются получателю. Получатель, зная закон соответствия между сообщениями и сигналами, может извлечь содержащуюся в сообщении информацию. Для верного декодирования каждому сигналу должно соответствовать одно определенное сообщение.
Преобразование сообщений в сигналы осуществляется с помощью кодирования и модуляции. Кодирование представляет собой отображение дискретных сообщений последовательностью символов позиционной системы счисления.
Последовательность символов, сопоставляемая одному элементарному сообщению (букве, знаку и т.д.) называется кодовой комбинацией. Систему правил преобразования элементарных сообщений в кодовые комбинации называют кодом. Основание используемой системы счисления называют основанием кода. Как правило, первичные коды задаются в виде таблиц.
При выборе основания системы счисления учитывают простоту, удобство и экономичность реализации цифрового представления информации в системе, ее преобразований и передачи по каналам связи. Наибольшее применение в технике передачи дискретной информации нашли колы с основанием 2, которые называются двоичными или бинарными. Поэтому в дальнейшем во всех случаях, где это не будет оговорено, рассматриваются двоичные коды. Символы двоичных кодов единица (1) и нуль (0) называются единичными элементами. Количество единичных элементов, образующих кодовую комбинацию, называется длиной кодовой комбинации.
Кодирование сообщений производится специальным устройством, которое называется кодером (кодирующим устройством) источника сообщения (датчика информации). В кодере кодовые комбинации представляются в виде определенных состояний накопительных элементов (триггеров, ферритов, механических рычагов, линеек и т.д.). Для передачи сообщения состояния накопительных элементов преобразуются в последовательность элементов дискретного электрического сигнала, как правило, в импульсы тока или напряжения. Каждый символ кодовой комбинации представляется единичным элементом цифрового сигнала. Процесс преобразования элементов кодовой комбинации в последовательность элементов сигнала называется модуляцией. (Ранее применялся и термин манипуляция).
В кодирующем устройстве производится первичное кодирование и первичная модуляция. Термин «первичное» подчеркивает то обстоятельство, что в процессе передачи по каналу связи сигналы, как правило, подвергаются дополнительному кодированию и модуляции.
Коды можно разделить на две большие группы: простые и корректирующие. Корректирующие коды (называют также помехоустойчивые) применяют для повышения верности информации. Простые коды (называют также: первичные, обыкновенные, безызбыточные) используются для первичного преобразования дискретных сообщений в сигналы и получаются на выходе кодера источника сообщения.
Простые код» делят на равномерные и неравномерные.
Равномерными называются такие коды, в которых все кодовые комбинации имеет одинаковую длину, т.е. имеют одинаковое число единичных элементов.
Неравномерными называют такие коды, кодовые комбинации которых могут отличаться одна от другой числом единичных элементов.
Оценка простых кодов производится по скорости передачи, помехоустойчивости и сложности технической реализации.
1.2.2. Равномерные простые коды
Как следует из определения, простые равномерные коды состоят из комбинаций одинаковой длины. Естественно, возникает вопрос:
Хорошо это или плохо?» Для ответа на этот вопрос рассмотрим следующий пример.
Пусть имеется некоторое сообщение, состоящее из М элементов, представляющее собой некоторую последовательность m(m