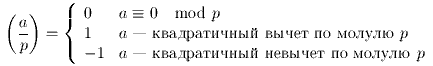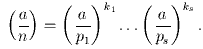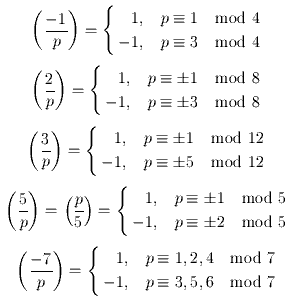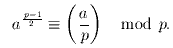тест соловея штрассена c код
СОДЕРЖАНИЕ
Простые методы
Например, рассмотрим число 100, которое без остатка делится на эти числа:
2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2
Хотя этот метод требует около p модульных умножений, что делает его непрактичным, теоремы о простых числах и модульных вычетах составляют основу многих других практических методов.
Пример кода
Python
Ниже приведен тест на простоту в C # с использованием той же оптимизации, что и выше.
JavaScript
Ниже приведен тест на простоту в JavaScript с использованием той же оптимизации, что и выше.
Ниже приведен тест на простоту на R (язык программирования) с использованием той же оптимизации, что и выше.
Эвристические тесты
Селфридж, Карл Померанс и Сэмюэл Вагстафф вместе предлагают 620 долларов за контрпример. Проблема остается открытой по состоянию на 11 сентября 2015 г.
Вероятностные тесты
Базовая структура рандомизированных тестов на простоту выглядит следующим образом:
Тест на простоту Ферма
Простейшим вероятностным тестом на простоту является тест на простоту Ферма (на самом деле тест на составность). Это работает следующим образом:
Тест на простоту Миллера – Рабина и Соловея – Штрассена.
Тест на простоту Фробениуса
Тесты на простоту Миллера – Рабина и Соловея – Штрассена просты и намного быстрее, чем другие общие тесты на простоту. Одним из методов дальнейшего повышения эффективности в некоторых случаях является тест псевдопримальности Фробениуса ; цикл этого теста занимает примерно в три раза больше времени, чем цикл Миллера-Рабина, но достигает границы вероятности, сравнимой с семью циклами Миллера-Рабина.
Тест на простоту Baillie-PSW
Другие тесты
Быстрые детерминированные тесты
Агравал, Каял и Саксена предлагают вариант своего алгоритма, который будет работать в Õ ((log n ) 3 ), если гипотеза Агравала верна; однако эвристический аргумент Хендрика Ленстры и Карла Померанса предполагает, что он, вероятно, неверен. Модифицированная версия гипотезы Агравала, гипотеза Агравала – Поповича, все еще может быть верной.
Сложность
В теории сложности вычислений формальный язык, соответствующий простым числам, обозначается как PRIMES. Легко показать, что PRIMES находится в Co-NP : его дополнение COMPOSITES находится в NP, потому что можно определить составность, недетерминированно угадав фактор.
Теоретико-числовые методы
Тест на первичность | Комплект 4 (Соловай-Штрассен)
Мы уже знакомились с тестированием на примитивность в предыдущих статьях этой серии.
Тест примитивности Соловея – Штрассена является вероятностным тестом для определения того, является ли число составным или, возможно, простым.
Прежде чем углубляться в код, нам нужно понять некоторые ключевые термины и концепции, чтобы иметь возможность кодировать этот алгоритм.
Символ Лежандра : Этот символ определен для пары целых чисел a и p, таких что p простое. Обозначается (a / p) и рассчитывается как:
Символ Якобиана : этот символ является обобщением символа Лежандра, где p заменяется на n, где n
тогда якобианский символ определяется как:
Если n взять за простое число, то якобиан будет равен символу Лежандра. Эти символы имеют определенные свойства —
1) (a / n) = 0, если gcd (a, n)! = 1, следовательно (0 / n) = 0. Это потому, что если gcd (a, n)! = 1, то должно быть некоторое простое число pi такой, что пи делит и а и п. В этом случае (a / pi) = 0 [по определению символа Лежандра].
2) (ab / n) = (a / n) * (b / n). Это может быть легко получено из факта (ab / p) = (a / p) (b / p) (здесь (a / p) — Легендарный Символ).
3) Если a чётно, то (a / n) = (2 / n) * ((a / 2) / n). Можно показать, что:
Алгоритм:
Мы выбираем число n для проверки его простоты и случайное число a, которое лежит в диапазоне [2, n-1], и вычисляем его якобиан (a / n), если n — простое число, то якобиан будет равен к Лежандру, и он будет удовлетворять условию (i), заданному Эйлером. Если он не удовлетворяет данному условию, то n является составным, и программа остановится. Как и любой другой вероятностный тест на простоту, его точность также прямо пропорциональна количеству итераций. Поэтому мы запускаем тест в течение нескольких итераций, чтобы получить более точные результаты.
Примечание: нас не интересует вычисление якобиана четных чисел, поскольку мы уже знаем, что они не простые, кроме 2.
псевдокод:
Реализация:
// C ++ программа для реализации Solovay-Strassen
// Тест на простоту
#include
using namespace std;
// по модулю для выполнения двоичного возведения в степень
long long modulo( long long base, long long exponent,
exponent = exponent / 2;
// Для вычисления символа якобиана заданного числа
int calculateJacobian( long long a, long long n)
return ans; // (1 / n) = 1
if (n % 8 == 3 || n % 8 == 5)
if (a % 4 == 3 && n % 4 == 3)
// Выполнить тест примитивности Соловая-Штрассена
bool solovoyStrassen( long long p, int iterations)
// Генерируем случайное число а
long long jacobian = (p + calculateJacobian(a, p)) % p;
int iterations = 50;
long long num1 = 15;
long long num2 = 13;
if (solovoyStrassen(num1, iterations))
if (solovoyStrassen(num2, iterations))
# Python3 программа для реализации Solovay-Strassen
# Тест на первичность
# функция по модулю для выполнения двоичного
# возведение в степень
def modulo(base, exponent, mod):
if (exponent % 2 = = 1 ):
exponent = exponent / / 2 ;
# Для вычисления якобианского символа
# номер
def calculateJacobian(a, n):
return 0 ; # (0 / n) = 0
return ans; # (1 / n) = 1
if (n % 8 = = 3 or n % 8 = = 5 ):
if (a % 4 = = 3 and n % 4 = = 3 ):
# Выполнить Соловай-Штрассен
# Тест на первичность
def solovoyStrassen(p, iterations):
for i in range (iterations):
# Генерация случайного числа
jacobian = (p + calculateJacobian(a, p)) % p;
if (solovoyStrassen(num1, iterations)):
print (num1, «is prime » );
print (num1, «is composite» );
if (solovoyStrassen(num2, iterations)):
print (num2, «is prime» );
print (num2, «is composite» );
# Этот код предоставлен mits
// PHP-программа для реализации
// Соловай-Штрассен тест на первичность
// по модулю
// двоичное возведение в степень
// Для вычисления якобиана
// символ данного числа
// Выполнить Соловай-
// Strassen Primality Test
// Генерируем случайное число а
// Этот код предоставлен ajit
?>
Выход :
Время работы: Используя быстрые алгоритмы для модульного возведения в степень, время работы этого алгоритма составляет O (k · 
Точность: алгоритм может вернуть неправильный ответ. Если вход n действительно прост, то выход всегда будет корректным. Однако, если вход n является составным, то возможно, что выход будет неправильно, вероятно, простым. Тогда число n называется псевдопримарой Эйлера-Якоби.
Ссылки:
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное или вы хотите поделиться дополнительной информацией по обсуждаемой выше теме.
Исправить ошибки в тесте Миллера и тесте Соловея-Штрассена
Надо написать программу, которая имеет 2 алгоритма:
Я написал, но имеются какие-то ошибки. Не могли бы Вы посмотреть? За ранее спасибо.
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Сделал что-то типа теста. Если выбираю в ИЗМЕНЕНИЕ теста во втором вопросе, что правильный вариант.
Найти ошибки в тесте
В общем седня закончил второй курс Cisco (для малых сетей, CCNA2). Финальный тест сдал средненько.
1С Профессионал по платформе. Ошибки в тесте
Добрый день. Столкнулся со следующей проблемой При сдаче на сертификат 1С Профессионал по.

Всем привет! Решаю задачку на codeforces, не совсем понимаю почему при тестах мое решение не.
Вложения
 | Тест.rar (335.8 Кб, 101 просмотров) |
Simak63, не знаю найдется ли кто смелый переписать за вас полностью всю программу. Так как если исправить там все ошибки, то она как раз вся и перепишется.
Вы бы сами что-нибудь поделали, переделали чуток. Глядишь, народ и потянется.
Вложения
 | Тест.rar (300.4 Кб, 51 просмотров) |
Решение
Добавлено через 19 часов 21 минуту
Второй тест (Соловея-Штрассена).
НОД (алгоритм Евклида):
Повторение в программе-тесте, как исправить?
Программа тест читает вопросы из текстового файла, вопросов всего 20 шт. Проблема в том что она.
Парни, подскажите пожалуйста нубу на ошибки в тесте
Уже третий раз пытаюсь сдать тест и окончательно сам себя запутал. Зеленым отмечены мои ответы.

Доброго времени суток. Такая проблема: нужен в тесте таймер. Да не простой, а чтобы по истечении.
Рандом в тесте
У меня есть код, который запускает тест, но мне надо добавить так, чтобы вопросы выпадали на рандом.

При вводе этого теста: 1 10 1 1 1 1 1 1 1 1 1 1 Выводит: 10 А нужно: 10 R R R R R R R R R
Регистрация в тесте
Помогите создать регистрацию в тесте, что бы после окончания теста сохранялись результаты.
Тест Соловея-Штрассена
Доброго времени суток! Я реализую тест Соловея-Штрассена на простое число и у меня выдается ошибка синтаксиса. Не важно как бы я не передвигала строку, все равно ошибка.
Вот ошибка:
File » «, line 4
return «n составное»
^
SyntaxError: ‘return’ outside function
Помощь в написании контрольных, курсовых и дипломных работ здесь.

Надо написать программу, которая имеет 2 алгоритма: Тест Миллера.
Алгоритм Штрассена
Помогите, пожалуйста реализовать на паскале алгоритм Штрассена для умножения матриц.
Метод Штрассена
Ребят помогите сделать перемножение матриц методом Штрассена. И если можно оставьте комментарий на.
Алгоритм Штрассена
при n=2 она работает правильно, но когда n=4 она считает неправильно. там последний столбец.
Алгоритм Штрассена
Нужно сделать алгоритм Штрассена на windows forms! А то у меня не получается((
Алгоритм Штрассена
Доброго времени суток. Пожалуйста помогите с прогой. Это алгоритм Штрассена. Все работает хорошо.
Алгоритм Штрассена
Всем привет! В общем без лишних подробностей сразу к делу) Необходимо написать программу умножения.
Алгоритм Штрассена-Винограда
Добрый день всем, нужна помощ в написании алгоритма. Нужен алгоритм который не будет создавать.
Тест соловея штрассена c код
Таким образом, если брать числа порядка нескольких миллиардов, не имеющих делителей меньше 1000, то примерно половина таких чисел будет простой. Среди 18-значных чисел не имеющих делителей меньше 1000 более трети просты.
Важной задачей до сих пор остается разработка эффективных методов проверки простоты. Даже самый простейший из них – метод последовательного деления на все простые числа не так плох. Для проверки простоты числа n достаточно проверить делимость на все простые числа, меньшие квадратного корня из n. Так как простых чисел, меньших 2 32 всего 203 280 221 штуки, то для проверки простоты числа 64 требуется не более 200 млн. делений, то есть меньше секунды времени.
В современной критографии имеют практическое значение простые числа величиной до 2 1024 (
308 десятичных цифр), максимально до 2 3000 (
900 десятичных цифр). Таким образом, с практической точки зрения нам надо уметь проверять простоту чисел длиной до 1000 десятичных знаков. Для этого требуются уже другие методы.
Количество простых чисел, не превышающих x в теории чисел принято обозначать π(x). Приведем некоторые значения этой функции (подробнее, см.Computational projects):
| π(10 3 ) | π(10 6 ) | π(10 9 ) | π(2 32 ) | π(10 12 ) | π(10 15 ) | π(10 18 ) | π(2 64 ) |
|---|---|---|---|---|---|---|---|
| 168 | 78 498 | 50 847 534 | 203 280 221 | 37 607 912 018 | 29 844 570 422 669 | 24 739 954 287 740 860 | 425 656 284 035 217 743 |
Псевдопростые числа
Другими словами, пседопростые числа – это те, на которых предлженный метод проверки ошибается.
Псевдопростых чисел довольно много. Например, среди чисел меньших 2 32 псевдопростых по основанию 2 оказывается 10403 (на 200 млн. простых), среди чисел меньших 2 64 – 118 968 378 (на 4 · 10 17 простых) (см. Jan Feitsma).
Проверка по нескольким различным основаниям сокращает количество ошибок, но не радикально. Например, среди 10403 чисел меньших 2 32 псевдопростых по основанию 2, псевдопростыми и по основанию 3 оказывается 2318 штук.
Кратные множители псевдопростых чисел
Интересно отметить, что псевдопростые числа могут иметь кратные множители. Однако такие числа должны иметь весьма специальный вид.
Наименьшее число a, при котором не существует указанных пар (a,p) при p 10 – это 21. Конечно, вряд ли стоит ожидать, что таких пар нет ни для каких p, скорее всего, это лишь вопрос объема вычислений. Тем не менее, нет и никаких оснований считать, что такие пары существуют для всех a.
Более подробно об этом можно прочитать здесь (pdf).
Символы Якоби и Лежандра
При рассмотрении чуть более сложных методов уже никак не обойтись без этих понятий. Поэтому рассмотрим их вкратце. Для более детального рассмотрения можно обратиться, например к Википедии или к литературе там приведенной.
Определение. Для простого p и целого a определим символ Лежандра следующим образом:
Мультипликативность. 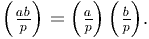
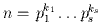
Частные случаи.
Тест Соловея-Штрассена
поэтому x ≡ ±1 mod p. На самом деле
Проверка этого соотношения для данного числа n и называется тестом Соловея-Штрассена («СШ(a)»).
На 203 миллиона простых, меньших 2 32 псевдопростых по основанию 2 всего 10403, из них тест Соловея-Штрассена проходят 5367 чисел.
Тест Миллера-Рабина
Так как кольцо вычетов по простому модулю является полем и, следовательно, не имеет делителей нуля, одна из этих скобок должна равняться 0. Эта проверка для данного числа n и называется тестом Миллера-Рабина («МР(a)»).
Тест Миллера-Рабина более сильный (включает в себя) чем тест Соловея-Штрассена.
Составные числа, проходящие тест Миллера-Рабина по основанию a называются сильно псевдопростыми числами (strong pseudoprimes, SPSP(a)).
Последовательности Люка (Lucas)
Теорема 3. Пусть 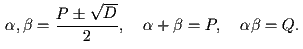
Последовательности Люка имеют множество интересных свойств. Все они довольно легко выводятся из этой формулы. Подробнее можно прочитать в книге
Paulo Ribenboim. My Numbers, My Friends. Popular Lectures on Number Theory (.pdf).
Основное достоинство такого метода проверки состоит в том, что он ошибается совсем на других числах, чем методы, основанные на теореме Ферма. Поэтому совместное применение методов Миллера-Рабина и Люка дает очень надежный результат.
На сегодняшний день нет ни одного примера, когда бы эти методы одновременно ошиблись!
Проверка простоты в языке Java
Так как все стандартные библиотеки языка Java поставляются вместе с исходными текстами, их реализацию можно подробно изучить (src.zip\java\math\BigInteger.java). Для работы с классом BigInteger не требуется никаких дополнительных библиотек, что так же является существенным фактором.
Приведем время выполнения ключевой операции modPow, на процессоре Intel i5 с тактовой частотой 2.27 ГГц (Win-64) в зависимости от разрядности чисел:
| Длина, бит | Время, мс |
|---|---|
| 64 | 0.008 |
| 128 | 0.034 |
| 256 | 0.14 |
| 512 | 0.75 |
| 1024 | 4.7 |
| 2048 | 35 |
Для вероятностной проверки чисел на простоту в языке Java служит метод класса BigInteger
Он работает следующим образом. Если проверяемое число имеет длину не больше 100 битов, то выполняется certainty/2 (но не более 50) тестов Миллера-Рабина по случайному основанию a.
Если число имеет длину больше 100 битов, то проверка выполняется в два шага. На первом опять же выполняется certainty/2 тестов Миллера-Рабина по случайному основанию a, но их предельное количество зависит от длины числа в битах:
После этих проверок, на втором шаге выполняется ещё и проверка методом Люка-Лемера :
Экспериментальный факт. В языке Java невозможно получить ошибку в методе isProbablePrime класса BigInteger для чисел длиннее 100 битов ни при каком уровне надежности большем 0.
И это неспроста, см. ниже, метод Фробениуса.
Метод Фробениуса
Квадратичные иррациональности
Определение. Квадратичной иррациональностью будем называть число вида z=a+b sqrt(c), где a,b,c – целые числа, причем c свободно от квадратов.
Через z mod n будем обозначать число (a mod n)+(b mod n) sqrt(c).
Сопряженным числом будем называть число z =a—b sqrt(c).
z 11 = 31648+18272 sqrt(3)
Вычисление z a mod n примерно вдвое сложнее, чем таже операция для целых чисел.
Тест Фробениуса
Теорему Фробениуса можно использовать для простроения вероятностного теста простоты числа.
Как и в других аналогичных тестах для повышения надежности можно было бы потребовать выполнить этот тест несколько раз с различными a,b (менять c нет смысла). Но это излишне.
На сегодняшний день не известно НИ ОДНОГО контрпримера к этому тесту!
Замечание. В книге
Richard Crandall; Carl Pomerance (2005). Prime numbers: A computational perspective (2nd ed.). Springer-Verlag. ISBN 0-387-25282-7
на стр. 146 контрпримеры приводятся. Однако тест Фробениуса в этом месте книги понимается в несколько другом смысле.
Учитывая отсутствие контрпримеров, вместо того, чтобы говорить о произвольном (случайном) выборе параметров a, b, c, мы их просто зафиксируем.
Определение. Пусть n – нечетное натуральное число, не являющееся полным квадратом. Его индексом Фробениуса IndF(n) будем называть наименьшее среди чисел [–1,2,3,4,5,6. ] такое, что символ Якоби jacobi(c/n) =–1.
Из мультипликативности символа Якоби следует, что если индекс c = IndF(n) положителен, то он прост.
Конечно, нас интересуют случаи, когда этот метод ошибается.
Определение. Составное нечетное натуральное число n назовем псевпопростым по Фробениусу (Frobenius pseudoprime, FPP), если оно просто по Фробениусу.
Отметим, что если n псевдопросто по Фробениусу, то n псевдопросто по основанию N(z), то есть тест Фробениуса включает в себя тест Ферма.
Гипотеза. Псевдопростых по Фробениусу чисел не существует!
Другими словами, тест Фробениуса никогда не ошибается.
Большой индекс Фробениуса
Ф-положительные делители
Напомню, что согласно определению, если jacobi(c/p)=1, то c является квадратом по простому модулю p, то есть существует d такое, что c ≡ d 2 mod p. Ф-положительные делители у псевдопростых по Фробениусу чисел должны удовлетворять некоторому условию, которое выполняется очень редко. Подробности здесь.
Кратные множители
Простые числа, удовлетворяющие этому условию встречаются редко, не удалось найти ни одного примера таких чисел. Прямым перебором можно получить следующее.