цифры в бинарном коде
Как объяснять двоичную систему счисления
Кто-то только входит в IT-мир, кто-то объясняет информатику своему чаду.
Довольно быстро вы обнаружите, что не так-то просто объяснить, как работает двоичный счёт.
Это вам очевидно, что после 11 идёт 100, а новичку это ещё долго может быть непонятно.
Так вот, чтобы увеличить скорость понимания, мы решили сделать дидактический материал.
Проблема
Важно отметить, что даже распиаренный курс Гарвардского университета по компьютерным наукам «CS50» не помогает.
Парень из американского университета просто заявляет, что «нуль — это нуль», «один — это один», а потом идёт 10, а потом 11. Понятно? Думаю, нет. Вот спросите кого-то, кто не программист, а каким будет следующее число — высока вероятность, что он не сможет ответить. Слишком быстро проскочили идею о переносе разряда.
То же самое касается школьных методов перевода: во-первых, методы эти академически сухи, во-вторых, не интуитивны — например, не очевидно, почему после каскадного деления на 2 нужно ставить биты задом наперёд.
А если непонятно, то и не интересно. А если нет интереса, то и запоминается с трудом.
Мы это всё учли, и решили сделать интересное и постепенное объяснение.
Что мы предлагаем
Сначала нужно объяснить, как вообще работает обычная десятичная система счисления — и про конечный «алфавит» цифр, и про идею переноса разряда. Так развивается понимание принципа «системы счисления».
Только потом можно переходить к идее двоичной системы — и вот обучаемый уже медленно, но довольно уверенно говорит «1, 10, 11, 100».
Далее, мы решили попробовать совсем не школьный метод — объяснение двоичного счёта на пальцах: это когда загнутый палец это 0, а разогнутый это 1.
Я проверял это на подростках: показываешь им: «это 1, это 2, это 3 — теперь покажите мне 4». И весь класс сосредоточенно, медленно показывает средние пальцы. Отличницы в эсхатологическом восторге, задние парты тыкают друг другу в лицо и кричат «на тебе четвёрку!».
Провокативно? Да. Запоминается? 100%.
Теперь, когда тема стала «своей», можно переходить к теме перевода чисел из одной системы счисления в другую — начать лучше с классического школьного сухого перевода (если честно, то больше чтобы постращать).
А уже потом с помощью анимации объяснить идею перевода прямо на пальцах, и потом опять же на пальцах пересчитать число 132 в средние пальцы уже на обеих руках.
На десерт показываем, где двоичная и 16-ричная системы применяется в реальной жизни.
Двоичная система — это например QR-коды вокруг нас.
А 16-ричная система это в основном коды цветов в CSS и хеши разных стилей, от MD5 до UUID.
Итак, вот весь пакет видео-уроков (они бесплатные, в Ютубе):
Двоичный код.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
Видя что-то впервые, мы зачастую задаемся логичным вопросом о том, как это работает. Любая новая информация воспринимается нами, как что-то сложное или созданное исключительно для разглядываний издали, однако для людей, желающих узнать подробнее о двоичном коде, открывается незамысловатая истина – бинарный код вовсе не сложный для понимания, как нам кажется. К примеру, английская буква T в двоичной системе приобретет такой вид – 01010100, E – 01000101 и буква X – 01011000. Исходя из этого, понимаем, что английское слово TEXT в виде двоичного кода будет выглядеть таким вот образом: 01010100 01000101 01011000 01010100. Компьютер понимает именно такое изложение символов для данного слова, ну а мы предпочитаем видеть его в изложении букв алфавита.
На сегодняшний день двоичный код активно используется в программировании, поскольку работают вычислительные машины именно благодаря ему. Но программирование не свелось до бесконечного набора нулей и единиц. Поскольку это достаточно трудоемкий процесс, были приняты меры для упрощения понимания между компьютером и человеком. Решением проблемы послужило создание языков программирования (бейсик, си++ и т.п.). В итоге программист пишет программу на языке, который он понимает, а потом программа-компилятор переводит все в машинный код, запуская работу компьютера.
Перевод натурального числа десятичной системы счисления в двоичную систему.
Чтобы перевести числа из десятичной системы счисления в двоичную пользуются «алгоритмом замещения», состоящим из такой последовательности действий:
1. Выбираем нужное число и делим его на 2. Если результат деления получился с остатком, то число двоичного кода будет 1, если остатка нет – 0.
2. Откидывая остаток, если он есть, снова делим число, полученное в результате первого деления, на 2. Устанавливаем число двоичной системы в зависимости от наличия остатка.
3. Продолжаем делить, вычисляя число двоичной системы из остатка, до тех пор, пока не дойдем до числа, которое делить нельзя – 0.
4. В этот момент считается, что двоичный код готов.
Для примера переведем в двоичную систему число 7:
1. 7 : 2 = 3.5. Поскольку остаток есть, записываем первым числом двоичного кода 1.
2. 3 : 2 = 1.5. Повторяем процедуру с выбором числа кода между 1 и 0 в зависимости от остатка.
3. 1 : 2 = 0.5. Снова выбираем 1 по тому же принципу.
4. В результате получаем, переведенный из десятичной системы счисления в двоичную, код – 111.
Таким образом можно переводить бесконечное множество чисел. Теперь попробуем сделать наоборот – перевести число из двоичной в десятичную.
Перевод числа двоичной системы в десятичную.
Для этого нам нужно пронумеровать наше двоичное число 111 с конца, начиная нулем. Для 111 это 1^2 1^1 1^0. Исходя из этого, номер для числа послужит его степенем. Далее выполняем действия по формуле: (x * 2^y) + (x * 2^y) + (x * 2^y), где x – порядковое число двоичного кода, а y – степень этого числа. Подставляем наше двоичное число под эту формулу и считаем результат. Получаем: (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 4 + 2 + 1 = 7.
Немного из истории двоичной системы счисления.
Двоичная система счисления
Двоичная система — это один из видов позиционных систем счисления. Основание данной системы равно двум, то есть используется только два символа для записи чисел.
Немного истории
Впервые о данной системе чисел заговорил основоположник математического анализа Г.В. Лейбниц еще в XVII веке. Он доказал, что для данного множества действуют все арифметические операции: сложение, вычитание, умножение и даже деление. Однако вплоть до 30-х годов XX века данную систему не рассматривали всерьез. Но с развитием электронных устройств и ЭВМ, ученые вновь принялись к изучению данной темы, так как двоичная система отлично подходила для программирования и организации хранения данных в памяти компьютеров.
Таблица и алфавит
Кроме того, двоичная система является самой удобной для быстрого перевода в другие системы счисления.
1001102 = 1 ∙ 2 5 + 0 ∙ 2 4 + 0 ∙ 2 3 + 1 ∙ 2 2 + 1 ∙ 2 2 + 0 ∙ 2 0 = 32 + 0 + 0 + 4 + 2 + 0 = 3810
Чтобы наоборот перевести число в двоичную из десятичной, необходимо выполнить его деление на 2 с остатком, а затем записать все остатки в обратном порядке, начиная с частного:
| Делимое | 38 | 19 | 9 | 4 | 2 |
|---|---|---|---|---|---|
| Делитель | 2 | 2 | 2 | 2 | 2 |
| Частное | 19 | 9 | 4 | 2 | 1 |
| Остаток | 0 | 1 | 1 | 0 | 0 |
Для перевода в другие системы необходимо:
Однако можно воспользоваться и более быстрым и удобным способом: разделить знаки двоичного числа на условные группы слева на право (для восьмеричной — по 3 знака; для шестнадцатеричной — по 4 знака), а затем воспользоваться таблицей перевода:
| Двоичная | Восьмеричная | Шестнадцатеричная |
|---|---|---|
| 0 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | |
| 1001 | 9 | |
| 1010 | A | |
| 1011 | B | |
| 1100 | C | |
| 1101 | D | |
| 1110 | E | |
| 1111 | F |
110010012 = 11 001 001 = 011 001 001 = 3118
110010012 = 1100 1001 = С916
Представление двоичных чисел
В двоичной системе также существует понятие «отрицательных» чисел. И для того, чтобы провести какую-либо операцию с ними в двоичном коде, необходимо представить его в виде дополнительного кода. Запись положительного числа при этом не меняется ни для одного из кодов.
Чтобы найти дополнительный код отрицательного числа, необходимо воспользоваться его прямым и дополнительным кодами.
Прямой код предполагает приписывание единицы в начале без изменений записи:
| A > 0 | Aпр = 0A | 1010112; Aпр = 01010112 |
| A ≤ 0 | Aпр = 1|A| | -1010112; Aпр = 11010112 |
Для записи обратного кода цифры заменяют на противоположное значение, первую единицу от прямого кода оставляют без изменений:
| A > 0 | Aобр = 0A | 1010112; Aобр = 01010112 |
| A ≤ 0 | Aобр = 1 A | -1010112; Aобр = 10101002 |
Дополнительный код предполагает использование обратного кода, с той лишь разницей, что к отрицательному числу прибавляют единицу:
| A > 0 | Aдоп = 0A | 1010112; Aдоп = 01010112 |
| A ≤ 0 | Aдоп = 1 A + 1 | -1010112; Aдоп = 10101012 |
Применение двоичной системы в информатике
Двоичная система получила особое распространение в программировании цифровых устройств, так как она соответствует требованиям многих технических устройств, поддерживающих два состояния (есть ток, нет тока). Кроме того, является более простой и надежной для кодирования информации. Именно поэтому программный код большей части ЭВМ основан именно на двоичной системе счисления.
Как читать двоичный (бинарный) код
Если вам интересно узнать, как читать двоичные числа, важно понять, как работают двоичные числа. Двоичная система известна как система нумерации «base 2», что означает наличие двух возможных чисел для каждой цифры; один или ноль. Большие числа записываются путем добавления дополнительных двоичных единиц или нулей.
Понимание двоичных чисел
Знание того, как читать двоичные файлы, не является критичным для использования компьютеров. Но хорошо понять концепцию, чтобы лучше понять, как компьютеры хранят числа в памяти. Он также позволяет понимать такие термины, как 16-битные, 32-битные, 64-битные и измерения памяти, такие как байты (8 бит).
Как читать двоичный код
«Чтение» двоичного кода обычно означает перевод двоичного числа в базовое 10 (десятичное) число, с которым люди знакомы. Это преобразование достаточно просто выполнить в своей голове, когда вы поймете, как работает бинарный язык.
Каждая цифра в двоичном числе имеет определенное значение, если цифра не является нулем. После того как вы определили все эти значения, вы просто складываете их вместе, чтобы получить 10-значное десятичное значение двоичного числа. Чтобы увидеть, как это работает, возьмите двоичное число 11001010.
2. Затем перейдите к следующей цифре. Если это один, то рассчитайте два в степени одного. Запишите это значение. В этом примере значение равно степени два, равной двум.
3. Продолжайте повторять этот процесс, пока не дойдете до самой левой цифры.
4. Чтобы закончить, все, что вам нужно сделать, это сложить все эти числа вместе, чтобы получить общее десятичное значение двоичного числа: 128 + 64 + 0 + 0 + 8 + 0 + 2 + 0 = 202.
Двоичные числа с подписью
Приведенный выше метод работает для базовых двоичных чисел без знака. Однако компьютерам нужен способ представления отрицательных чисел также с помощью двоичного кода.
Из-за этого компьютеры используют двоичные числа со знаком. В системе этого типа самая левая цифра известна как знаковый бит, а остальные цифры известны как биты амплитуды.
Чтение двоичного числа со знаком почти такое же, как и без знака, с одним небольшим отличием.
1. Выполните ту же процедуру, как описано выше для двоичного числа без знака, но остановитесь, как только вы достигнете самого левого бита.
2. Чтобы определить знак, осмотрите крайний левый бит. Если это единица, то число отрицательное. Если это ноль, то число положительное.
4. Бинарный метод со знаком позволяет компьютерам представлять числа, которые являются положительными или отрицательными. Однако он потребляет начальный бит, а это означает, что для больших чисел требуется немного больше памяти, чем для двоичных чисел без знака.
Бинарный код
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления натуральные числа записываются с помощью всего лишь двух символов (в роли которых обычно выступают цифры 0 и 1).
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и соответствует требованиям:
В цифровой электронике одному двоичному разряду в двоичной системе счисления соответствует один двоичный логический элемент (инвертор с логикой на входе) с двумя состояниями (открыт, закрыт).
Содержание
Таблица умножения двоичных чисел
Использование двоичной системы при измерении дюймами
При указании линейных размеров в дюймах по традиции используют двоичные дроби, а не десятичные, например: 5¾″, 7 15 / 16″, 3 11 / 32″ и т. д.
Преобразование чисел
Для преобразования из двоичной системы в десятичную используют следующую таблицу степеней основания 2:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Начиная с цифры 1 все цифры умножаются на два. Точка, которая стоит после 1 называется двоичной точкой.
Преобразование двоичных чисел в десятичные
Допустим, вам дано двоичное число 110011. Какому числу оно эквивалентно? Чтобы ответить на этот вопрос, прежде всего запишите данное число следующим образом:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | ||||
| 32 | +16 | +2 | +1 |
Затем, начиная с двоичной точки, двигайтесь влево. Под каждой двоичной единицей напишите её эквивалент в строчке ниже. Сложите получившиеся десятичные числа. Таким образом, двоичное число 110011 равнозначно 51.
Либо 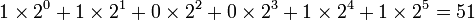
Преобразование методом Горнера
Для того, что бы преобразовывать числа из двоичной в десятичную систему данным методом, надо суммировать цифры слева-направо, умножая ранее полученный результат на основу системы (в данном случае 2). Например, двоичное число 1011011 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+0=22 >> 22*2+1=45 >> 45*2+1=91 То есть в десятичной системе это число будет записано как 91. Или число 101111 переводится в десятичную систему так: 0*2+1=1 >> 1*2+0=2 >> 2*2+1=5 >> 5*2+1=11 >> 11*2+1=23 >> 23*2+1=47 То есть в десятичной системе это число будет записано как 47.
Преобразование десятичных чисел к ближайшей степени двойки, неменьшей этого числа
Ниже приведена функция, возвращающая число, неменьшее аргумента, и являющееся степенью двух.
Преобразование десятичных чисел в двоичные
Допустим, нам нужно перевести число 19 в двоичное. Вы можете воспользоваться следующей процедурой :
Итак, мы делим каждое частное на 2 и записываем в остаток 1 или 0. Продолжать деление надо пока в делимом не будет 1. Ставим числа из остатка друг за другом, начиная с конца. В результате получаем число 19 в двоичной записи (начиная с конца): 10011.
Другие системы счисления
В статье «Системы счисления (продолжение)» [1] описываются преимущества и недостатки 4-ричной системы счисления по сравнению с двоичной в компьютерах, созданных Хитогуровым.
См. также
Ссылки
Полезное
Смотреть что такое «Бинарный код» в других словарях:
Код Грея — 2 битный код Грея 00 01 11 10 3 битный код Грея 000 001 011 010 110 111 101 100 4 битный код Грея 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 Код Грея система счисления, в которой два соседних значения… … Википедия
Пойнт-код — Код сигнальной точки (англ. Signal Point Code (SPC)) сигнальной системы 7 (SS7, ОКС 7) это уникальный (в домашней сети) адрес узла, используемый на третьем уровне MTP (маршрутизация) в телекоммуникационных ОКС 7 сетях для идентификации … Википедия
Бесквадратное число — В математике бесквадратным называется число, которое не делится ни на один квадрат, кроме 1. К примеру, 10 бесквадратное, а 18 нет, так как 18 делится на 9 = 32. Начало последовательности бесквадратных чисел таково: 1, 2, 3, 5, 6, 7,… … Википедия
Direct3D 10 — Для улучшения этой статьи желательно?: Викифицировать статью. Переработать оформление в соответствии с правилами написания статей. Исправить статью согласно стилистическим правилам Википедии … Википедия
Python — У этого термина существуют и другие значения, см. Python (значения). Python Класс языка: му … Википедия
Хакерская атака — в узком смысле слова в настоящее время под словосочетанием понимается «Покушение на систему безопасности», и склоняется скорее к смыслу следующего термина Крэкерская атака. Это произошло из за искажения смысла самого слова «хакер». Хакерская… … Википедия
Грей — (от англ. gray/grey серый) шотландская и английская фамилия. Содержание 1 Известные носители 2 Грей, как псевдоним известных людей … Википедия
Кодирование Голомба — Коды Голомба это семейство энтропийных кодеров, являющихся общим случаем унарного кода. Также под кодом Голомба может подразумеваться один из представителей этого семейства. Код Голомба позволяет представить последовательность символов в виде… … Википедия
Крэкерская атака — Хакерская атака в узком смысле слова в настоящее время под словосочетанием понимается «Покушение на систему безопасности», и склоняется скорее к смыслу следующего термина Крэкерская атака. Это произошло из за искажения смысла самого слова «хакер» … Википедия






