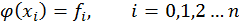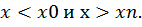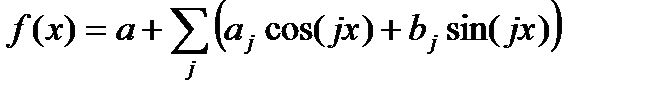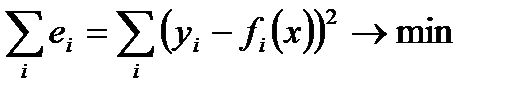Аппроксимация и интерполяция в чем разница

4. Интерполяция, аппроксимация и регрессия

Интерполяция, аппроксимация и регрессия

Нередко исходные данные при решении математических задач представлены рядом точек произвольной зависимости вида у(х). Сама по себе эта зависимость может быть неизвестной. Для вычисления промежуточных значений функции используется аппарат интерполяции. При нем истинная функция заменяется аппроксимирующей функцией, которая в узловых точках дает точные значения ординат и позволяет вычислить значения интерполируемой функции в промежуточных точках.

Полиномиальная интерполяция и аппроксимация

Для решения задач интерполяции и аппроксимации функций, заданных рядом узловых точек, в Mathematica используются следующие функции:

InterpolationOrder — опция функции Interpolation, указывающая степень подходящего полинома. При ее значении, равном 1, осуществляется кусочно-линейная интерполяция. Целое значение, большее единицы, задает степень глобальной полиномиальной интерполяции.

Применение основной функции Interpolation поясняет следующий пример:

Таким образом, на заданном отрезке изменения х функция Interpolation позволяет найти любое промежуточное значение функции funi [x], в том числе значения в узловых точках.

Теперь рассмотрим часто используемую полиномиальную аппроксимацию, при которой ищется полином, график которого точно проходит через узловые точки данных.

Степень интерполирующего (и аппроксимирующего) полинома всегда на 1 меньше числа узловых точек интерполяции или аппроксимации. Аппроксимация отличается от интерполяции тем, что предполагает получение аппроксимирующей функции в явном виде. При полиномиальной аппроксимации такой функцией является степенной многочлен.

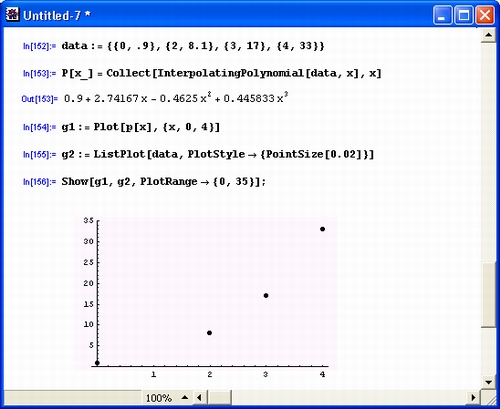
Пример на рис. 5.13 иллюстрирует технику проведения полиномиальной аппроксимации с применением интерполирующего степенного многочлена.

Рис. 5.13. Полиномиальная аппроксимация таблично заданных данных

Как и следовало ожидать, степень аппроксимирующего многочлена оказалась равной трем, поскольку было задано четыре пары данных. На рис. 5.13 представлено также сравнение результата полиномиальной аппроксимации с исходными данными. Исходные данные представлены на графике в виде точек, а зависимость, представленная аппроксимирующим полиномом, выведена сплошной линией.

В узлах интерполяции значения интерполирующего многочлена точно совпадают со значениями исходных данных. Однако это не гарантирует малую погрешность за пределами узловых точек (особенно при экстраполяции функций). Чем больше пар данных и чем выше степень аппроксимирующего многочлена, тем выше погрешность аппроксимации. Обычно аппроксимация при степени многочлена выше 8-10 не применяется из-за резкого возрастания погрешности. При большом числе пар исходных данных более полезной на практике является регрессия.

Регрессия и визуализация ее результатов

Еще один широко используемый вид аппроксимации — регрессия. Она заключается в нахождении параметров некоторой функции регрессии, при которой график этой функции проходит в «облаке» узловых точек, обеспечивая наименьшую среднеквадратичную погрешность их представления. В отличие от интерполяции, при регрессии найденная функция не дает точного значения ординат в узловых точках — она просто минимизирует погрешность вычислений в этих точках.

Для решения задач регрессии используется функция ядра

Эта функция ищет приближение для списка данных data методом наименьших квадратов в виде линейной комбинации функций funs переменных vars. Данные data могут иметь форму <, <х2, у2. f2 >. >, где число координат х, у. равно числу переменных в списке vars. Также данные data могут быть представлены в форме с одной координатой, принимающей значения 1, 2. Аргумент funs может быть любым списком функций, которые зависят только от объектов vars.

Следующие примеры показывают приближение исходных данных степенным полиномом и линейной комбинацией двух функций:

0. 997273-1.40864 х+2.33409 х2

0.9ех + 2.89276х- 1.08392 х2

Здесь в первом примере выполняется полиномиальная регрессия со степенью полинома, равной 2. Максимальная степень на 1 меньше числа пар исходной зависимости (в нашем случае их 4) — при такой степени регрессия вырождается в обычную полиномиальную аппроксимацию, которая рассматривалась ранее.

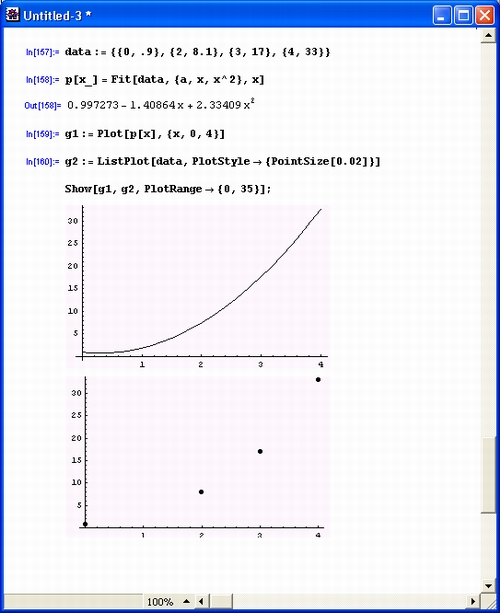
Рисунок 5.14 показывает несколько иной путь проведения полиномиальной аппроксимации — исходные данные заданы объектом-списком data.

В конце документа рис. 5.14 показано построение графика аппроксимирующего полинома второй степени и точек исходных данных. Заметно, что при регрессии график полинома проходит в середине «облака» исходных точек и не укладывается на них точно.

В уроке 12 будут рассмотрены дополнительные функции для проведения регрессии. Они входят в различные пакеты расширения системы Mathematica 3/4.

Рис. 5.14. Полиномиальная регрессия с графическим выводом

Источник

Аппроксимация и интерполяция данных. Основные определения

Любому специалисту в своей практической деятельности приходится изучать зависимости между различными параметрами исследуемых объектов, процессов и систем. Например: зависимость числа оборотов двигателя от нагрузки, т.е. n=f(Мкр.); зависимость силы резания при обработке детали на металлорежущем станке от глубины резания, т.е. P=f(t), и т.д.

Из всех способов задания зависимостей наиболее удобным является аналитический способ задания зависимости в виде функции n=f(Мкр.), P=f(t), y=f(t).

Однако на практике специалист чаще всего получает зависимости между исследуемыми параметрами экспериментально. В этом случае ставится натурный эксперимент, изменяются значения параметров на входе системы, измеряются значения параметров на выходе системы. Результаты измерений заносятся в таблицу.

Таким образом, в результате проведения натурного эксперимента получаем зависимости между исследуемыми параметрами в виде таблицы, т.е. получаем, так называемую, табличную функцию.

Далее с этой табличной функцией необходимо вести научно-исследовательские расчеты. Например, необходимо проинтегрировать или продифференцировать табличную функцию и т.д.

При такой постановке задачи моделирования нужно заменить табличную функцию аналитической. Для этой цели используются методы аппроксимации и интерполяции.

Аппроксимация – это замена исходной функции f(x) функцией φ(x) так, чтобы отклонение f(x) от φ(x) в заданной области было наименьшим. Функция φ(x) называется аппроксимирующей.

Если исходная функция f(x) задана таблично (дискретным набором точек), то аппроксимация называется дискретной. Если исходная функция f(x) задана аналитически (на отрезке), то аппроксимация называется непрерывной или интегральной.

Интерполяция – это замена исходной функции f(x) функцией φ(x) так, чтобы φ(x) точно проходила через точки исходной функции f(x).

Интерполяция еще называется точечной аппроксимацией.

Точки исходной функции f(x) называются узлами интерполяции.

Для интерполирующей функции справедливо

Экстраполяцией называется аппроксимация вне заданной области определения исходной функции, т.е.

Найдя интерполяционную функцию, мы можем вычислить ее значения между узлами интерполяции, а также определить значение функции за пределами заданного интервала (провести экстраполяцию).

Основной мерой отклонения функции y(x) от функции f(x) при аппроксимации является величина, равная сумме квадратов разностей между значениями аппроксимирующей и исходной функций

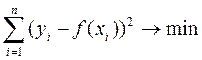Простейшими видами интерполяции является линейная и квадратичная.

При линейной интерполяции точки заданной функции соединяются линейными отрезками, и функция f(x) приближается ломаной с вершинами в данных точках. В качестве уравнения интерполяционного многочлена используются уравнения прямой, проходящей через две точки.

При квадратичной интерполяции в качестве приближающей функции, соединяющей соседние точки, принимается квадратный трехчлен. Такая интерполяция называется параболической.

Распространенным видом интерполяции является интерполяция с использованием кубических сплайн-функций.

Сплайн представляет собой модель гибкого тонкого стержня из упругого материала, закрепленного в двух соседних узлах интерполяции с заданными углами наклона α и β так, чтобы потенциальная энергия стержня была минимальна.

Интерполяция может выполняться с помощью многочленов Ньютона, Эрмита, Лагранжа и т.д.

Наиболее известными методами аппроксимации являются метод наименьших квадратов, метод многочленов Чебышева, рядов Тейлор и т.д.

При решении задач аппроксимации часто используются функции регрессии.

Регрессия – представление совокупности данных некоторой функцией f(x).

Задачей регрессии является вычисление параметров функции f(x) таким образом, чтобы функция приближала последовательность исходных точек с наименьшей погрешностью. При этом функция f(x) называется уравнением регрессии.

При регрессии не требуется чтобы функция проходила через все заданные точки, что особенно важно при аппроксимации данных, заведомо содержащих ошибки.

Источник

Интерполяция, аппроксимация и экстраполяция

Хотя в отличие от теоретической физики, которая исследует математические модели природы, экспериментальная физика призвана исследовать саму природу, но конечной целью эксперимента, по большому счету, является поиск математических моделей, описывающих экспериментальные результаты. Мы ограничимся поиском функциональной зависимости при обработке экспериментальных данных.

При отсутствии предварительных сведений о характере функциональной зависимости решение о выборе обычно принимается исходя из наименьшего расхождения с экспериментом и требуемой точности совпадения. При наличии сведений о такой зависимости гораздо разумнее подбирать параметры именно для такой зависимости, даже если принципиально иная зависимость обеспечивает большую точность, поскольку коэффициенты иной зависимости могут заведомо не иметь физического смысла и не помогут в интерпретации данных.

Интерполяция

Интерполяция (от слова inter, т.е. «через») это замена данных функцией, проходящей через определенные точки.

При интерполяции для представления информации о функции ¦(x) используется таблица значений этой функции в точках:

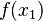Задачей является построение по таблице такой функции , которая бы не сильно отличалась от ¦, оставаясь равной ей в приведенных точках.

При интерполяции методом ближайшего соседа за значение функции берется значение функции ¦(x) в точке, ближайшей к рассматриваемой.

При кусочно-линейной интерполяции значение ¦(x) интерполируется линейной функцией по двум соседним с точкой x точкам:

Кусочно-линейная интерполяция обычно применяется только при необходимости пересчитать имеющиеся данные к массиву с другим шагом, чтобы иметь возможность, например, поделить одни данные на другие, если они получены при разных входных значениях, но в одном диапазоне величин.

Интерполяция полиномами – обобщенный случай линейной интерполяции, в котором линейная функция заменяется полиномом высшего порядка. В нашем случае через 7 точек можно провести полином 6го порядка. Вычисление полинома проводится по интерполяционным формулам Ньютона или через интерполяционный многочлен Лагранжа. Очевидно, что с ростом числа точек сложность растет экспоненциально.

Основная идея сплайн-интерполяции функций – построение кусочно-полиномиальной интерполяции, при которой остается непрерывной функция ¦(x) и несколько ее первых производных. Для этого в точках сшивки должны быть равны соседние полиномы и их производные. Обычно для этого достаточно уже полинома третьего порядка (т.н. кубическая сплайн-интерполяция).

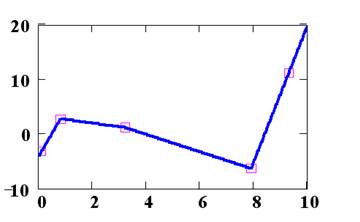
Тригонометрическая интерполяция востребована в случае, когда данные носят периодический характер. Она же – интерполяция полиномом Фурье. Интерполирующая функция представляет собой сумму конечного числа гармоник ряда Фурье:

Во многих случаях, особенно в последнем, возможна неоднозначная интерполяция функцией.

При обработке двухмерных данных применяют билинейную и бикубическую интерполяции, при обработке трехмерных – трилинейную, а также многомерную сплайн-интерполяцию (рис. 29).

Рис. 29 Методы интерполяции. Слева направо – метод ближайшего соседа, линейная и кубическая. Верхний ряд – интерполяция одномерных данных, нижний – двумерных [24]

Аппроксимация

Аппроксимация (от слова approx – «примерно») это поиск функции, по возможности приближенной к имеющемуся набору данных. Аппроксимация удобна, когда имеется большой массив данных, или в случае, если приведенные выше натурные данные служат опорными точками для выявления функциональной зависимости (а также в случае, когда зависимость заведомо известна).

Аппроксимация возможна с помощью любых подходящих функций, например полиномов определенного порядка. Результатом аппроксимации нулевого порядка будет константа, первого порядка – прямая с наклоном, второго – парабола. При количестве точек на одну больше порядка результатом будет интерполяция.

Для оптимального подбора параметров уравнений обычно используют метод наименьших квадратов (МНК), в котором ищут такие параметры функции, при которых квадрат отклонения минимизируется:

При аппроксимации крайне важно верно выбрать аппроксимирующую функцию, т.к. если она не описывает модель, то интерпретация данных будет затруднена.

Экстраполяция

Экстраполяция – разновидность аппроксимации, при которой функция рассчитывается вне заданного интервала, а не между точками. В зависимости от аппроксимирующей или интерполирующей функции результаты экстраполяции будут различаться. Но заметнее всего изменения именно вне диапазона точек данных. Поэтому с данными экстраполяции надо обращаться аккуратно.

Вопросы для самопроверки:

· Какой вид обработки данных ведет к экспоненциальному росту расчетов при увеличении числа точек?

· Какие требования к интерполяционным функциям при кубической сплайн-интерполяции?

· Что является результатом аппроксимации второго порядка?

· Какие методы вы бы рекомендовали для выявления неизвестной функциональной зависимости?

АТОМНО-СИЛОВая МИКРОСКОПИя

В последние десятилетия широкое применение для исследования геометрических параметров наноразмерных структур получили сканирующие зондовые микроскопы (СЗМ). Они позволяют получать трехмерные топографические изображения поверхности с высоким пространственным разрешением, вплоть до отображения атомных структур. Наиболее известными из зондовых приборов являются атомно-силовой микроскоп (АСМ) и сканирующий туннельный микроскоп (СТМ). СТМ предназначен для получения изображения поверхности проводящих образцов и основан на принципе зависимости величины туннельного тока от расстояния между зондом и образцом. Работа АСМ основана на силовом взаимодействии зонда и образца и позволяет получать изображения безотносительно к физико-химическим свойствам материала поверхности, что особенно важно при исследовании полупроводниковых структур, а также модифицировать поверхность. Кроме того, в отличие от всех других типов СЗМ, в АСМ изображение формируется путем измерения исключительно разности высот на поверхности в процессе сканирования её зондом. Это является существенным преимуществом по сравнению с традиционно используемыми оптическими и электронными микроскопами, в которых механизм формирования контраста может искажать топографию [25].

АСМ изобретен Гердом Биннингом и Кристофом Гербером в 1986 году. Физический принцип работы АСМ — силовое взаимодействие между поверхностью образца и специальным зондовым датчиком – острием, жестко закрепленным на конце упругой консоли, или кантилевере. В упрощенном виде данное взаимодействие можно представить в виде потенциала Леннарда-Джонса — модели взаимодействия двух неполярных молекул, описывающей зависимость энергии взаимодействия от расстояния между частицами:

,

Рис. 30. Зависимость силы взаимодействия острия зонда и образца от расстояния и основные режимы работы

На больших расстояниях между острием и образцом доминируют силы притяжения, на малом — силы отталкивания. Эти силы уравновешиваются при расстоянии порядка двух ангстрем. В зависимости от используемого расстояния «зонд-образец» АСМ может работать в одном из следующих режимов: контактном, полуконтактном и бесконтактном. В контактном режиме кантилевер с зондом прижимается к образцу и его отклонение вызвано взаимным отталкиванием атомов острия иглы и поверхности в результате перекрывания их электронных оболочек и кулоновского отталкивания ядер. В этом режиме изгиб кантилевера с зондом на конце непосредственно отражает отталкивающую силу и используется для отображения рельефа поверхности.

В полуконтактном режиме зонд колеблется перпендикулярно поверхности на частоте собственного механического резонанса, попеременно находится в притягивающем/отталкивающем интервале и «ощущает» контактные отталкивающие силы только в течение короткой части периода колебаний (т.н. «телеграфный режим» — tapping mode). В бесконтактном режиме колеблющийся зонд находится на расстоянии преимущественного действия притягивающих сил. В полуконтактном и бесконтактном режимах измеряется не величина прогиба кантилевера, а изменения амплитуды, частоты и фазы колебаний кантилевера с острием, которые возникают из-за воздействия сил притяжения на гармонический осциллятор, которым является кантилевер, при приближении к поверхности.

В бесконтактном режиме острие может колебаться как в направлении нормали к поверхности, так и поперек нормали. Режим поперечных колебаний называют поперечно-силовой микроскопией или микроскопией бокового сдвига (shear force).

В зависимости от вида отслеживаемого взаимодействия АСМ-методики также делятся на несколько групп: визуализация топографических, отталкивающих, торсионных (приводящих к скручиванию кантилевера), электрических, магнитных, упругих, вибрационных свойств, трения и пр. С помощью АСМ возможно и проведение литография. Так, применение специальных прочных зондов позволяет царапать или изменять поверхность, а изменение прикладываемого к зонду напряжения позволяет перемещать по поверхности отдельные атомы.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Источник

20. Интерполяция и аппроксимация функциональных зависимостей.

Интерполяция, экстраполяция и аппроксимация

Вычисление многих функций, особенно специальных, требует больших затрат времени. Поэтому до сих пор широко применяются таблицы таких функций. Достаточно отметить знаменитые на весь мир таблицы в книге «Справочник по специальным функциям с формулами, графиками и таблицами» под редакцией М. Абрамовица и И. Стиган [59].

Если некоторая зависимость у(х) представлена рядом табличных отсчетов y(x), то интерполяцией принято называть вычисление значений у(х) при заданном х, расположенном в интервале между отсчетами. За пределами общего интервала определения функции [а,b], то есть при х b, вычисление у(х) называют экстраполяцией (или иногда предсказанием значений функции). В данном случае речь идет об одномерной интерполяции, но возможны двумерная интерполяция функций двух переменных z(x, у) и даже многомерная интерполяция для функций многих переменных.

Интерполяция и экстраполяция часто выполняются по некоторой скрытой, но подразумеваемой зависимости. Например, если узловые точки функции соединить отрезками прямых, то будем иметь многоинтервальную линейную интерполяцию данных. Если использовать отрезки параболы, то интерполяция будет параболической. Особое значение имеет многоинтервальная сплайн-интерполяция, области применения которой уже сейчас весьма обширны и непрерывно расширяются. Интерполяция рядом Фурье (набором синусоидальных функций) также достаточно хорошо известна; она эффективна при интерполяции периодических функций.

Аппроксимацией в системах компьютерной математики обычно называют получение приближенных значений какого-либо выражения. Однако под аппроксимацией функций подразумевается получение некоторой конкретной функции, вычисленные значения которой с некоторой точностью аналогичны аппроксимируемой зависимости. Обычно предпочитают найти одну зависимость, приближающую заданный ряд узловых точек. Часто для этого используют степенные многочлены — полиномы.

Здесь мы будем рассматривать такие виды аппроксимации, которые дают точные значения функции у(х) в узловых точках в пределах погрешности вычислений по умолчанию. Если аппроксимирующая зависимость выбирается из условия наименьшей среднеквадратической погрешности в узловых точках (метод наименьших квадратов), то мы имеем регрессию или приближение функций по методу наименьших квадратов.

Источник

Интерполяция и аппроксимация

3. Интерполяция и аппроксимация

3.1. Понятие натурного и вычислительного эксперимента.

Человечество познавало окружающий мир и самого себя в этом мире на основе статистики, которая позволяла ему находить связи между явлениями. Статистика при посредстве человеческого разума породила современную науку – астрономию и математику, физику и генетику.

Поколения астрономов по мере совершенствования приборов и физических представлений о земных законах постепенно могли выявлять законы, по которым живет Солнечная система, хотя до сих пор не могут гарантировать отсутствие неизвестных планет или объяснить происхождение пояса астероидов. Физик XVIII столетия, одержимый некоторой идеей (возникшей явно не на пустом месте), или его последователи могли многочисленными экспериментами установить или опровергнуть ее истинность, хотя и здесь абсолютная истина недостижима – корпускулярная и волновая теория света тому пример. Тем не менее, из наблюдений за страшными молниями и искрами от шерсти ласковой кошки, в итоге проб и ошибок, родилась практически вся современная техника.

Итак, наблюдая и фиксируя какие-то явления, человек решал прямую задачу исследования. Он набирал факты. А далее человеку приходилось решать обратную задачу – воспроизведение закона, которому следовала или следует некоторая система (астрономическая, техническая, экономическая и пр.). Понятно, что по результатам действий системы (часто неполным и искаженными внесистемными факторами) невозможно гарантировать однозначность получаемых выводов при решении обратной задачи.

Тем не менее, человек, если есть возможность, проводит натурный эксперимент, чтобы набрать статистику, которая даст информацию для формулирования закона, которому следует то или иное явление, с целью получения формулы, с помощью которой можно предсказать будущее.

Но не надо забывать, что натурное экспериментальное исследование справедливо только в пределах условий проведенного эксперимента. Иными словами, экспериментальное исследование – тоже модель и поэтому не следует преувеличивать результаты экспериментальных исследований.

Наряду с натурными экспериментами проводятся вычислительные эксперименты. Вычислительный эксперимент приобретает исключительное значение в тех случаях, когда натурные эксперименты и построение физической модели оказываются невозможными.

Проведение вычислительного эксперимента является сложным исследованием и включает в себя несколько этапов:

для исследуемого объекта строится модель, обычно сначала физическая (мысленно, на бумаге), фиксирующая разделение всех действующих в рассматриваемом явлении факторов на главные и второстепенные, которые на данном этапе исследования отбрасываются. Одновременно формулируются допущения и условия применимости модели, границы, в которых будут справедливы полученные результаты. Модель записывается в математических терминах (как правило, в виде дифференциальных или интегро-дифференциальных уравнениях). Очевидно, что создание математической модели проводится специалистами, хорошо знающими данную область естествознания или техники, а также математиками, представляющими себе возможности решения математической задачи. Разрабатывается метод решения сформулированной математической задачи. Эта задача представляется в виде совокупности алгебраических формул, по которым должны вестись вычисления и условия, показывающие последовательность применения этих формул; набор этих формул и условий носит название вычислительного алгоритма. Разрабатываются алгоритм и программа решения задачи на компьютере. Программирование решений определяется теперь не только искусством и опытом исполнителя, а перерастает в самостоятельную науку со своими принципиальными подходами. Проведение расчетов на компьютере. Результат получается в виде некоторой цифровой информации. Точность информации определяется при вычислительном эксперименте достоверностью модели, положенной в основу эксперимента, правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания). Обработка результатов расчетов, их анализ и выводы. Здесь полученную информацию представляют в наиболее понятном виде, помогающем установить вид зависимостей между входными и выходными параметрами математической модели. Лучше в виде графиков. На этом этапе могут возникнуть необходимость уточнения математической модели (усложнения или, наоборот, упрощения), предложения по созданию упрощенных инженерных способов решения и формул, дающих возможности получить необходимую информацию более простым способом.

Решению задач последнего этапа посвящены целые разделы математики, большая часть которых, к сожалению, не изучается студентами в обычных технических и экономических университетах.

3.2. Цели и методы математической обработки результатов вычислительного эксперимента

Целью любого эксперимента является определение качественной и количественной связи между исследуемыми параметрами, либо оценка численного значения какого-либо параметра.

В некоторых случаях вид зависимости между переменными величинами известен по результатам теоретических исследований. Как правило, формулы, выражающие эти зависимости, содержат некоторые постоянные, значения которых и необходимо определить из опыта.

Другим типом задачи является определение неизвестной функциональной связи между переменными величинами на основе данных эксперимента. Такие зависимости называют эмпирическими.

Однозначно определить неизвестную функциональную зависимость между переменными невозможно даже в том случае, если бы результаты эксперимента не имели ошибок. Тем более не следует этого ожидать, имея результаты эксперимента, содержащие известные ошибки, возникающие в процессе вычислений.

Поэтому следует четко понимать, что целью математической обработки результатов вычислительного эксперимента далеко не всегда является нахождение истинного характера зависимости между переменными или абсолютной величины какой-либо неизвестной.

Целью математической обработки чаще всего является представление результатов наблюдений в виде наиболее простой формулы или значения неизвестной с оценкой возможной погрешности ее использования.

Для простоты дальнейшего изложения будем считать, что некоторое явление характеризуется только двумя ве­ли­чи­на­ми <Х>и , связанными между собой некоторой неизвестной функциональной зависимостью. Любую из этих величин с одинаковой сте­пенью можно считать независимой, тогда как другая будет считаться за­ви­си­мой.

Различают четыре типа зависимостей между переменными:

1)Зависимость между неслучайными переменными, не требующую для своего изучения применения статистических методов;

2) Зависимость случайной переменной y от неслучайных переменных, исследуемую методами регрессионного анализа;

3) Зависимость между случайными переменными y и x, изучаемую методами корреляционного анализа;

4) Зависимость между неслучайными переменными, когда все они содержат ошибки измерения, требующую для своего изучения применения конфлюэнтного анализа.

Вычислительный эксперимент проводится обычно при заданных исходных данных, которые в дальнейшем можно рассматривать в некотором приближении как неслучайные величины.

Результаты же сложного расчета (вычислительного эксперимента), выполненного с помощью, например, метода конечных элементов, в сильнейшей степени зависят от множества факторов, в частности, от ошибок дискретизации и математического представления рассчитываемого объекта, ошибок округления, ошибок усечения, ошибок во входных данных и многих других ошибок, вплоть до ошибок в программировании. Поэтому такие результаты можно рассматривать как уже некие случайные величины.

Поэтому при обработке результатов численного эксперимента чаще всего приходится обращаться к методам регрессионного анализа.

Основу же большинства перечисленных выше методов составляют методы интерполирования и среднеквадратичной аппроксимации.

Пусть в результате какого-либо сложного эксперимента (в том числе и вычислительного) получена серия данных, которые мы можем представить в виде точек на плоскости в координатах осей x и y. Здесь координаты xi и yi точек считаются соответственно входными и выходными параметрами модели.

Понятно, что можно предположить, что эти точки принадлежат какой-то неизвестной функции. По сути, имеют таблицу значений xi и yi и говорят, что работают с таблично заданной функцией.

Очень часто возникает задача по­до­брать не­ко­торую простую функцию, кото­рая, во-первых, име­ла бы в известных точ­ках за­дан­ные значения, во-вторых, позволяла находить промежуточные значения функции и в-третьих могла бы показать, как будет изменяться эта функция вне пределов интервала по х, где проводился эксперимент. Понятно, что простая функция вы­чис­лялась бы быстрее, проще, и дешевле, нежели проведение эксперимента

Источник