Что показывает коэффициент корреляции в эконометрике
Корреляция между временными рядами: что может быть проще?
Предварительные замечания
Сказ о том, почему я не справился с оформлением
Для начала, я внимательно прочитал все советы для новичков о том, как оформить статью. Я честно старался им следовать. Подготовив статью в гуглдоках, я проверил текст, расставил ссылки и примечания, добавил формулы и картинки, предварительно сохраненные в habrastorage. После чего воспользовался рекомендованным хабраконвертером.
Ладно, приступим к вставке рисунков. Оформляя статью в гуглдоках, я заранее загрузил их на habrastorage. Теперь надо только открыть хранилище и добавить ссылки в статью. На всякий случай, вхожу в хранилище и. где мои файлы, загруженные в прошлый раз? Их нет (см. скриншоты)! Хотя я всегда логинился под своим именем.
Ну ладно, у всех бывают свои причуды. Очевидно, хранилище Хабра считает излишним хранить историю загрузок пользователя. Но я же все-таки не совсем идиот. В прошлый раз при загрузке изображений я предусмотрительно скопировал прямые ссылки на них. И, понятно, проверил, что эти ссылки работают. Точнее, что они работали сразу после загрузки изображений:
Вы знаете, это все-таки слишком.
Однако потратив полный рабочий день на подготовку статьи, я не готов потратить еще два раза по столько на преодоление барьера хабраредактора. Как бы высоко я не оценивал местное сообщество, я просто не вижу смысла осваивать ущербный ретроредактор в качестве теста на профпригодность. Невольно закрадывается сомнение в уровне профессионализма команды Хабра, которая не может (или не хочет?) дать новым пользователям простые и понятные инструменты для оформления публикаций. Или хотя бы доходчиво объяснить, как пользоваться теми, что есть. Но если так, то стоит ли прилагать столько усилий, чтобы стать частью такого сообщества?
UPD: Спасибо модераторам! Со мной связались и на часть вопросов ответили: Наш старший модератор подправил вёрстку до публикации — что возможно в рамках нового редактора. То описание, что вы приводили, оно актуально для старого редактора. Мы сейчас в процессе миграции, поэтому не всё окончательно железобетонно реализовано.
Благодаря модераторам, большинство багов с оформлением получилось исправить! А все высказанные выше замечания к первоначальной версии редактора можно теперь рассматривать как мой баг-репорт 😉
Связь между количеством морских пиратов и глобальной температурой кажется очевидной. Интересно, что для пиратства в области авторских прав (на рисунке не показаны) корреляция с потеплением намного более сильная, только вот знак корреляции будет противоположный
Введение
Содержание:
Дополнительное замечание про распределения: нормально ли, что анализируя данные геофизического мониторинга, мы никогда не встретимся с нормальным распределением?
Часть 1 – необходимая тривиальщина
Если вы еще не совсем забыли прочитанное в учебниках по статистике, можете смело этот раздел пропустить, и переходить сразу к части 2-ой.
Как известно, математика невероятно эффективно описывает реальность. Построив абстрактную математическую модель, мы отвлекаемся от всего несущественного, и это позволяет нам не только лаконично выразить свойства моделируемого объекта на языке формул, но часто также и сделать далеко идущие выводы о закономерностях его поведения. Сказать, что такие выводы полезны для практики – это не сказать ничего. Буквально вся окружающая нас сейчас техника была бы невозможна без математики, транслирующей физические законы и их следствия в тот формат, который можно непосредственно применять для разных практических нужд.
Одна из базовых математических абстракций, с изучения которой начинается любой курс матстатистики – это понятие случайной величины. Считается, что получая значение случайной величины результате какого-то измерения, или эксперимента, мы извлекаем его из некоторого пространства элементарных событий. Очень важно, что при повторении опыта мы извлекаем новое значение случайной величины из той же самой генеральной совокупности. Именно этот – тривиальный, казалось бы, факт – позволяет нам строить очень мощные и крайне полезные статистические критерии. В частности, мы можем вычислять произвольные функции одной или нескольких случайных величин и делать определенные выводы о поведении этих функций.
Например, чтобы оценить наличие связи между двумя случайными величинами X и Y, мы можем вычислить коэффициент Rxy корреляции между ними. Для независимых случайных величин с не слишком экзотическими свойствами значение Rxy будет обычно приближаться к нулю по мере роста объема той выборки, по которой мы оцениваем Rxy. Прелесть и мощь математики проявляется в том, что, имея самую минимальную информацию об исходных случайных величинах (достаточно знать их функцию распределения), мы можем точно сказать, как именно (по какому закону) будет приближаться к нулю Rxy, если X и Y действительно независимы. Например, если X и Y имеют нормальное распределение, то 95%-ный доверительный уровень z95 можно приблизительно оценить по формуле:
где N – это количество пар измерений в выборке (будем считать, что их достаточно много). Говоря простыми словами, если мы оценим коэффициент корреляции Rxy между X и Y по выборке, содержащей 100 пар значений, то для независимых X и Y лишь в 5% случаев (т.е. в каждой 20-й выборке) модуль Rxy окажется больше 0.2.
и вовсе будет превышено лишь в 1% случаев. Поэтому, получив в такой ситуации Rxy=0.4 (то есть, намного выше, чем z), мы говорим, что произошло очень редкое и маловероятное, в рамках выдвинутой гипотезы, событие. Настолько редкое, что гипотеза о независимости X и Y (иногда ее называют «нулевая гипотеза»), скорее всего, неверна, и ее надо отвергнуть. Именно так обычно доказывают, что X и Y статистически связаны.
Мало-мальски искушенный читатель, наверно, уже начинает зевать: зачем я опять повторяю известные вещи? Все сказанное выше, действительно, очень похоже на правду. Однако, как говорили еще в древнем Риме, тут не вся правда.
Первый (и очень важный) подводный камень состоит в том, что наши расчеты (которые только что привели к противоречию) на самом деле опирались не только на предположение о независимости случайных величин X и Y, но также еще и на предположение о нормальности их распределения. Аномальное (в рамках нашей модели) значение Rxy действительно говорит, что модель, по всей видимости, неверна. Однако ошибка может быть в любом месте. Вполне возможно, что в X и Y действительно независимы, просто они имеют другое (не гауссовское) распределение. При котором значение Rxy=0.4 при объеме выборки N=100 вполне обыденно и типично.
до попадания в стенку
Интересно, что если слегка изменить условия, и ввести на стене-мишени ось координат с нулем в основании перпендикуляра, опущенного от пушки на стену, и определить L, как значение на этой оси, то матожидание L теперь будет просто нулем. А дисперсия – все равно бесконечна. Для любознательных предлагаю задачку: попробуйте построить «антоним» нашей случайной величины, с конечной дисперсией, но бесконечным матожиданием. Возможно ли это?
К счастью для большинства аналитиков, столь экзотические распределения в обычной практической жизни встречаются редко. Бывает, что распределение может оказаться, например, равномерным, однако это не очень сильно повлияет на уровни значимости z статистики Rxy. Они лишь немного изменятся по сравнению со значениями, рассчитанными для гауссовых X и Y. Конечно, есть еще проблема «тяжелых хвостов», или выбросов, но она сравнительно просто может быть решена выбраковкой таких значений перед началом анализа.
Так все-таки, нужно ли проверять функцию распределения исходных случайных величин на нормальность? Формально, конечно, да. Но могу вас заверить, что для достаточно длинного экспериментального ряда (если, конечно, это не выходной сигнал гауссовского генератора белого шума) такая проверка всегда покажет, что распределение достоверно отличается от нормального. Поэтому общепринятый метод заключается в том, что в такой ситуации уровни значимости все равно вычисляются по стандартным формулам для случайных величин с гауссовым распределением. А затем оговаривается, что поскольку условия применимости этих формул немного нарушены, реальная значимость вместо 99%-ной может оказаться, например, 97%-ной. Считается, что такие различия не играют особой роли, если рассчитанный уровень значимости превышается многократно. Например, если при объеме выборки 10000 корреляция Rxy=0.25 (а оценка 3/sqrt(N) дает значение z99=0.03), то исходную гипотезу о независимости X и Y все равно можно смело отвергнуть. Ведь значение z превышено на порядок!
Буквоеды, конечно, скажут, что подобный вывод не является математически строгим. Но реальный мир всегда отличается от абстрактной модели. При обработке результатов любого эксперимента мы неизбежно должны принимать какие-то допущения, доказать которые невозможно. Вот и в описанном выше примере, несмотря на отсутствие строгости, этот вывод будет верным по существу, так как для действительно независимых случайных величин X и Y такое событие (Rxy=0.25 при объеме выборки 10000) практически невероятно ни при каком разумном распределении X и Y.
Ну что, переходим к расчетам?
Часть 2. Критерий истины – практика
А теперь приведу пару фактов, сопоставление которых друг с другом полностью разрушает только что сформулированную, такую стройную и прекрасную картину нашего модельного мира.
Факт первый: при числе измерений порядка 10000 для любых независимых случайных величин с «адекватным» распределением (имеются в виду распределения, похожие на равномерное или нормальное, без гигантских выбросов и т.п.) вероятность получения |Rxy| > 0.1 исчезающе мала. Во всяком случае, она существенно меньше, чем 0.01.
Факт второй: если посчитать коэффициент корреляции между любыми геофизическими параметрами, для которых имеются достаточно длинные ряды наблюдений, то сплошь рядом окажется, что Rxy по модулю больше, чем 0.1. Иногда – много больше. Причем, это верно для любых пар рядов. В зависимости от конкретного набора параметров, такие «суперзначимые» корреляции могут наблюдаться в половине всех случаев или даже в трех четвертях. Точная цифра не имеет значения – ведь согласно теории вероятностей, для действительно независимых величин они должны обнаруживаться чуть чаще, чем никогда. Так что же, все до одного геофизические параметры правда взаимозависимы? Погодите немного с ответом.
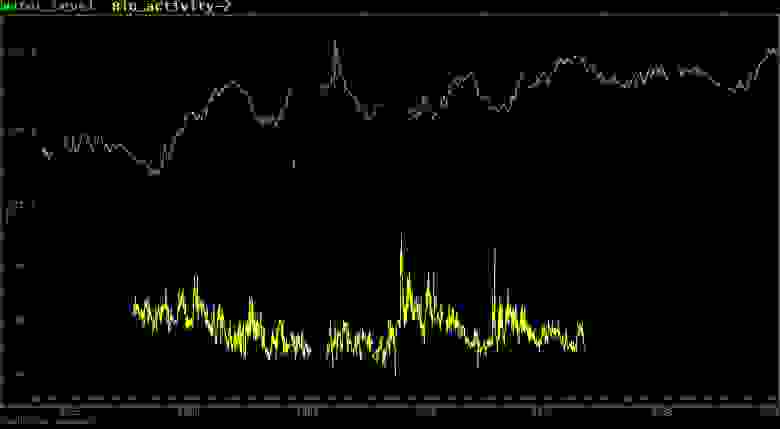
Не будем зацикливаться на геофизике. Посчитаем, к примеру, коэффициент корреляции между уровнем воды в скважине на Камчатке и активностью тараканов в аквариуме в подвале лаборатории на Памире (активность измерялась автоматически, непрерывно в течение 5 лет, в рамках эксперимента по прогнозу землетрясений биологическим способом):
Уровень воды в скважине на Камчатке (вверху) и двигательная активность колумбийских тараканов (внизу). Двигательная активность измерялась автоматически, в рамках эксперимента по прогнозу землетрясений биологическим способом
Внезапно, корреляция равна Rxy= –0.35 при числе измерений около 20 000:
А вот для уровня активности сомиков в соседнем аквариуме расчеты дают значение Rxy= +0.16. Знак корреляции изменился, но это тоже на порядок выше формального 99%-ного уровня значимости. Неужели животные как-то чувствуют происходящее в скважине за тысячи километров?!
Дальше еще интереснее. Возьмем ряды чисел микроземлетрясений, произошедших в 1975-1985 годах в нескольких сейсмоактивных районах, и формально их сдвинем по времени лет на 20 (просто добавим поправку к календарю). Теперь прокоррелируем эти ряды, например, с изменениями солнечного радиоизлучения на волне 2800 МГц (10.7 см) в 1955-1965 гг. Здравый смысл говорит, что после такого сдвига всякая корреляция должна исчезать. А вот и неправда! Сами значения Rxy при сдвиге, разумеется, поменяются. Но они все равно на порядки выше формальных 99%-ных уровней значимости. Хотя ни о какой причинно-следственной связи при подобном временном сдвиге
и речи не может быть
Те же зашкаливающие корреляции наблюдаются и практически для любых социальных процессов, а также в эконометрике. Правда, тут длина временных рядов по объективным причинам намного меньше – десятки, в лучшем случае сотни точек. Зато можно коррелировать практически что угодно! Например, успеваемость школьников в Нижневартовске с урожаем кокосов на Филиппинах. А среднегодовую заболеваемость легочными инфекциями в Санкт-Петербурге (возьмем наблюдения за последние 30 лет) с – индексом Доу-Джонса. Впрочем, вместо индекса Доу-Джонса с тем же успехом можно подставить в формулы урожайность пшеницы во Франции в двадцатом веке (только добавьте +100 к номеру года), или поголовье овец в Австралии в девятнадцатом (тут уже придется добавить две сотни). Можно даже проделать небольшой трюк, и интерпретировать число 1899 (и другие номера лет), как номер суток, считая с определенной даты. Если подобрать начальную дату так, чтобы этот ряд хронологически совместился с количеством вызовов скорой помощи в сутки в среднем российском городе (для которого вам повезет найти эти данные), итоговый вывод от этого не изменится! То есть, пробуя коррелировать разные случайно выбранные пары достаточно длинных экспериментальных рядов, мы будем лишь изредка получать Rxy, близкий к нулю. Гораздо чаще коэффициент корреляции будет намного выше любых формальных
Необходимое уточнение: «гораздо чаще» получится, только если наблюдений достаточно много – десятки и сотни тысяч отсчетов. Чем короче ряды, чем меньше значение N, тем выше значение z. Поэтому для коротких рядов вероятность, что коэффициент корреляции случайно попадет в интервал [-z, +z], возрастает.
Получается, что абсолютно любые процессы взаимосвязаны? Только для доказательства наличия «значимой» корреляции нужно нарастить длину ряда? Но как тогда быть с примерами, где мы просто «сдвинули» ряд во времени или вообще подменили шаг временной шкалы? Ведь речь тут идет уже не о синхронных процессах (при очень большом желании, поверить в связь школьников и кокосов все-таки можно), а именно о случайно наложенных друг на друга произвольных экспериментальных сигналах?!
Я понимаю, что у половины читателей рука уже тянется к пистолету, чтобы приставить его к виску автора и потребовать доказательства, то есть данные. Сразу скажу, что данных в табличном виде не будет. Оригинальные данные я не имею права выкладывать в сеть (но их описание и картинки можно найти, например, вот тут: раз, два, три). А давать ссылки на общедоступные данные просто не вижу смысла – всегда можно возразить, что они специально подобраны. Однако, вы легко можете проверить написанное выше, прокоррелировав между собой пару десятков случайно выбранных рядов долговременных наблюдений практически любых природных и/или социальных процессов, доступных в Сети. Чем более длинные серии вы загрузите, тем ощутимее окажется разница между корреляциями, ожидаемыми для случайных независимых переменных, и фактически полученными значениями Rxy. Самое сложное, что вам придется для этого сделать – это импортировать данные в выбранную программу статистического анализа. После этого расчет коэффициента корреляции обычно выполняется
нажатием одной кнопки
Кому интересно сделать чуть больше – например, посмотреть корреляционное поле в динамике или поиграться с модифицированными сигналами – могу предложить для расчетов нашу программу анализа временных рядов. Она позволяет более аккуратно, чем типовые статистические пакеты, работать с рядами, содержащими пропущенные наблюдения и другие дефекты, а также имеет несколько дополнительных фишек, полезных при работе с календарными шкалами времени (таких, как автоматическая синхронизация данных, согласование скважности у разных рядов и т.д.). Но сразу предупрежу, что это специализированный продукт для работы с данными долговременного мониторинга, и его «порог входа» заметно выше обычного.
Впрочем, пора уже вспомнить о другой половине читателей, которые не поленились проверить мои утверждения (или просто поверили на слово), и теперь пребывают в сомнении когнитивного диссонанса. Ведь расчеты сделаны стопроцентно надежными методами, а достоверность данных не вызывает ни малейших сомнений. При этом причинная связь между рядами абсолютно исключена (особенно, когда они сдвинуты на столетия). И несмотря на все это, корреляция в доброй половине случаев просто зашкаливает. Боюсь, что рука у них уже тоже тянется к пистолету, только дуло направлено не в сторону автора, а к собственному виску.
Так вот, НЕДЕЛАЙТЕЭТОГО!
Прочтите сначала третью часть этого опуса. Я очень старался написать ее так, чтобы предотвратить ненужные жертвы!
Часть 3. А вот и ответы
Наверно, многие уже поняли, к чему я клоню. Для остальных я сначала сформулирую правильный вывод, а уже потом его обосную. На самом деле, все вышеописанные «недоразумения» объясняются тем, что мы пытаемся применять аппарат, предназначенный для работы со случайными величинами, для анализа случайных процессов.
Главное, что отличает случайный процесс от случайной величины – процесс явным образом зависит от времени. Проводя наблюдения за каким-то природным явлением, мы вовсе не извлекаем получаемые значения из одной и той же генеральной совокупности. Даже если настройки прибора и положение датчиков не менялись, состояние измеряемого объекта в каждый новый момент времени будет другое. Попросту говоря, это будет уже другая случайная величина. Серию измерений, выполненных одним и тем же прибором, даже неподвижно стоящим под одной и той же горой, нельзя рассматривать, как серию выборок из одного и того же пространства элементарных событий. Это – основная причина, почему привычные статистические методы в этом случае не работают.
Повторю еще раз другими словами. Для описания случайного процесса, в отличие от случайной величины, недостаточно задать его функцию распределения один раз. Просто потому, что в разные моменты времени t она может быть разной. А еще для случайного процесса надо определить функцию совместного распределения вероятностей для моментов времени t и t+dt и так далее. Чтобы оценить эти функции, наблюдая за случайным процессом, нужна не одна реализация, а целый ансамбль. Ну, хотя бы десяток реализаций. Причем, это обязательно должны быть реализации одного и того же случайного процесса. Тогда и только тогда для каждого момента времени у нас будет несколько измерений одной и той же случайной величины. Как их обрабатывать дальше, мы уже знаем из школьного вузовского курса статистики.
Но что же делать, если у нас есть только одна Земля, одна Камчатка, один Памир? Как изучать взаимосвязи между процессами, каждый из которых мы наблюдаем в единственном экземпляре?! (тут должна быть театральная пауза 😉
Не буду врать, что над этим вопросом издревле размышляли лучшие умы человечества. Однако кое-какие способы выкрутиться из этой подставы все же имеются. Оказывается, что для некоторых классов случайных процессов, все характеристики которых неизменны во времени, наличие ансамбля не обязательно! То есть, нам не потребуется десять реализаций, чтобы оценить какую-нибудь статистику. Вместо этого достаточно некоторое время понаблюдать за одной! Например, чтобы оценить коэффициент корреляции между X и Y, достаточно иметь одну реализацию X и еще одну – Y. Что, собственно, все мы и делаем, когда вычисляем коэффициент корреляции между потеплением и пиратами. Ну или рыбками на Памире и уровнем в скважине на Камчатке.
Если процесс позволяет такие трюки, то он называется эргодическим. Иногда различают эргодичность по среднему, по дисперсии и т.д. При анализе наблюдений очень часто априори считается, что исследуемые процессы являются эргодическими. Иногда это даже не оговаривается специально.
Но если мы хотим избежать грубейших ошибок, то нельзя забывать, что гипотеза эргодичности – это только гипотеза. Подавляющее большинство долговременных наблюдений продолжается конечное время (вы поняли, это такая шутка), а на выходе получается единственный ряд. Доказать эргодичность такого процесса в принципе невозможно. Поэтому, начиная анализ данных, мы чаще всего просто постулируем ее явным образом или неявно. А что еще остается делать, если в наличии куча данных и руки чешутся начальник требует срочно использовать всю мощь безупречного, многократно проверенного теоретиками статистического инструментария для достижения практических целей?
Ну а теперь пришло время поставить финальную точку.
На самом деле, все упомянутые в этой статье временные ряды (как, впрочем, и подавляющее большинство других подобных сигналов) вовсе не являются эргодическими. И если доказать эргодичность процесса достаточно сложно (я бы сказал, практически нереально), то вот опровергнуть ее часто можно без особых усилий. Достаточно просто вспомнить, что практически все экспериментальные временные ряды существенно нестационарны. Огромный массив накопленных экспериментальных данных однозначно свидетельствует, что априорная «базовая модель» почти любого природного процесса – это вовсе не белый шум (для которого действительно можно заигрывать с эргодичностью). Нет, спектры большинства реальных сигналов имеют
А именно, спектральная мощность W пропорциональна периоду T в некоторой положительной степени b. В электронике, геофизике и во многих других прикладных областях показатель степени b чаще всего лежит где-то между 0.5 и 2.0. В предельном случае (когда показатель степени b=2), мы имеем процесс с независимыми случайными приращениями. Для такого процесса каждое следующее значение (в момент времени t+1) состоит из значения в момент времени t и случайной добавки. Про такой процесс говорят, что он имеет бесконечную память. Но если текущие значения ряда зависят от предыдущих, то такой процесс нельзя считать стационарным.
Примеры модельных рядов со степенным спектром. Степенной параметр b подписан на графиках
На этом рисунке приведены примеры модельных рядов с различным степенным показателем b, сгенерированных по алгоритму Фосса. Видно, что чем больше значение b, тем очевиднее нестационарность сигнала. Но если ряд не стационарен, то он заведомо не может рассматриваться, как последовательность измерений одной и той же случайной величины. Для него совершенно бессмысленно оценивать те статистики, которые вводятся и исследуются при анализе случайных величин.
Да, конечно, мы можем формально подставить измеренные значения в формулы, и даже посчитать что-то внешне напоминающее Rxy. Однако каким будет теоретическое распределение этой статистики, никому не известно.
Ясно только, что классические доверительные границы в этом случае считать бесполезно. Они просто не имеют никакого отношения к делу, так как мы имеем все основания отвергнуть «нулевую модель» вне зависимости от того, получится ли у нас |Rxy| >> z, или же будет Rxy = 0. Ведь занявшись анализом временных рядов, мы уже вышли за пределы этой модели, сформулированной для работы со случайными величинами. А это значит, что полная (правильная) формулировка модели теперь должна включать не два, а три постулата. А именно,
ЕСЛИ выполнены три условия:
У1) X и Y статистически независимы
У2) какое-нибудь ограничение на функции распределения X и Y
У3) X и Y – это случайные величины
(т.е. анализируемая выборка составлена из пар (Xi, Yi), извлеченных из одной и той же генеральной совокупности)
Вполне очевидно, что когда мы рассматриваем временные ряды, для которых не доказана эргодичность (тем более, есть прямые свидетельства нестационарности), третье условие заведомо нарушается. Этого более чем достаточно, чтобы отклонить сформулированную модель, даже не вычисляя значение Rxy.
Часть 4. И еще раз про доказательство от противного
К сожалению, у меня нет таланта писать доступно и кратко. А донести свою мысль все-таки хочется. Поэтому давайте попробуем заново проследить всю логику доказательства наличия статистической связи между переменными X и Y методом корреляций.
Первый шаг доказательства заключается в том, что мы формулируем некоторый набор требований, или предположений, о характеристиках X и Y. В число этих предположений входит и допущение о том, что они статистически независимы.
На втором шаге мы берем экспериментальные данные и вычисляем некоторую совместную статистику X и Y. В данном случае это – статистика Rxy.
Третий шаг состоит в вычислении функции распределения Rxy при условии, что все сформулированные ранее допущения – например, условия У1, У2 и У3 – истинны.
На четвертом шаге мы сравниваем фактически полученное значение Rxy с теоретическим распределением этой величины. Если оказывается, что вероятность случайно наблюдать именно такое значение Rxy пренебрежимо мала, то отсюда делается вывод, что не все исходные допущения истинны. Проще говоря, что хотя бы одно из условий У1, У2 и У3 – ложно.
Наконец, если у нас нет абсолютно никаких сомнений в истинности всех прочих предположений, кроме допущения о статистической независимости X и Y, то мы делаем вывод об ошибочности именно этого допущения. То есть, если мы уверены в истинности У2 и У3, то ложным должно быть условие У1. Что, собственно и означает: связь есть!
Теперь понятно, почему эта схема «сбоит» при работе с нестационарными временными рядами. Сравнивая вычисленный коэффициент корреляции с теоретическими уровнями значимости z, мы не учитываем, что теоретическое распределение z рассчитано для одной модели, а коэффициент корреляции Rxy вычислен совсем для другой. Если упустить из вида этот нюанс, можно получать «значимые корреляции» через раз. Что порою и наблюдается даже в статьях, напечатанных в рецензируемых научных журналах.
Если у вас остается еще хоть капля сомнений, или вы просто не любите абстрактные рассуждения, проведите простой
со случайными, независимыми, но не эргодическими рядами. Возьмите полсотни реализаций белого шума S(t) длиной по миллиону значений (t=0,1. 1000000). Проинтегрируйте каждую такую реализацию по правилу: P(0)=0, P(t+1)=P(t)+S(t). И потом посчитайте значение парного коэффициента корреляции для случайно взятых рядов P(t). Или для их фрагментов (только не слишком коротких). Просто по построению, все эти ряды и фрагменты абсолютно независимы друг от друга. Можно даже не вычислять, чему равен уровень значимости z для коэффициента корреляции Rxy при подобном объеме выборки. Так как первый же тест покажет разницу на порядки. Надеюсь, мне не нужно дополнительно пояснять, что полученный результат совершенно не связан с возможной неидеальностью генератора случайных чисел?
Похожий, но чуть менее впечатляющий результат можно получить и для рядов с другими значениями степенного параметра спектра в пределах обычного для геофизических наблюдений диапазона b=[0.5, 2.0]. Все дело в том, что такие ряды, в простонародном названии – фликкер-шум, страдают так называемой низкочастотной расходимостью спектра. Это значит, что на любом интервале времени максимальную амплитуду имеют те вариации, чья характерная длительность сопоставима с длиной ряда. Если мы рассматриваем ограниченную во времени серию наблюдений, это очень похоже на линейный тренд. А корреляция между двумя линейными трендами, как известно, всегда равна ±1. Точнее, оценивать корреляцию для линейно спадающих или растущих функций бессмысленно. Чтобы построить линейную функцию, нужно ровно две точки, которые и определяют число степеней свободы процесса. Можно до бесконечности увеличивать частоту дискретизации такого сигнала, – количество информации (= число независимых значений данных) от этого не изменится. Поэтому в формулу для оценки уровня значимости z коэффициента корреляции Rxy в этом случае надо подставлять значение N=2. Ну и чему равно z в таком случае?
Как говорится, вот то-то же и оно.
Впрочем, и после вычитания линейного тренда фликкер-шумовой ряд вовсе не станет стационарным. Так как останутся периоды, близкие к половине длины ряда и т.д. А ведь кроме фликкер-шумовой «базы», в большинстве реальных геофизических, макроэкономических и других подобных сигналов обычно присутствуют также и периодические компоненты, иногда весьма мощные (сезонная, суточная, приливная и т.д.); сплошь и рядом встречается экспоненциальный тренд и другие особенности, камня на камне не оставляющие от надежды на стационарность. И, тем более, на эргодичность.
В сухом остатке
Для оценки статистик случайного процесса одной реализации, вообще говоря, недостаточно! Это почти то же самое, как оценивать дисперсию случайной величины по единственному ее измерению. Чтобы использовать методы матстатистики, нужен целый пакет рядов (ансамбль реализаций случайного процесса). Если речь идет о парной статистике (корреляция между X и Y), нужен ансамбль из пар временных рядов. Располагая таким набором, мы можем оценивать коэффициент Rxy корреляции между случайными процессами X и Y, как функцию времени t. А вот говорить о корреляции случайных процессов безотносительно момента времени t, в общем случае, беспредметно. Так как значения Rxy в разные моменты времени t, вообще говоря, будут разные.
Увы, но на практике у нас обычно имеется только одна Вселенная и только одна реализация каждого временного ряда. Чтобы использовать статистические методы при работе с такими данными, приходится опираться на гипотезу эргодичности. Она предполагает, что вместо вычисления какой-то статистики (например, среднего) по ансамблю реализаций, мы можем взять один ряд, усреднить по времени, и получить то же самое. Если ряд эргодический, этот подход реально работает!
Проблема, однако, в том, что почти любые сигналы, получаемые при долговременных наблюдениях за геофизическими, макроэкономическими и многими другими процессами, практически никогда не удовлетворяют условию эргодичности. Применяя при обработке подобных данных стандартный аппарат матстатистики, ориентированный на манипуляции со случайными величинами, запросто можно не просто «сесть в лужу», но и получить совершенно абсурдные результаты. И вовсе не потому, что эти методы чем-то плохи. Все дело в том, что неосторожно подменяя случайную величину случайным процессом, мы безоговорочно выходим за рамки дозволенного, грубо нарушая условия применимости этих методов.
Если так, то как же тогда анализировать подобные временные ряды, спросите вы? Нестационарные, с трендами, сезонными и суточными циклами, и т.д.? Как искать связь между ними и оценивать ее значимость? Хороший вопрос. Я постараюсь написать об этом в следующей статье. Если, конечно, такая тематика будет интересна читателям Хабра.
P.S. Автор благодарит за полезные замечания и советы И.Цуркиса. При оформлении коллажа использована картинка с вот этого сайта.
Дополнительное замечание про распределения:
нормально ли, что анализируя данные геофизического мониторинга, мы никогда не встречаемся с нормальным распределением?